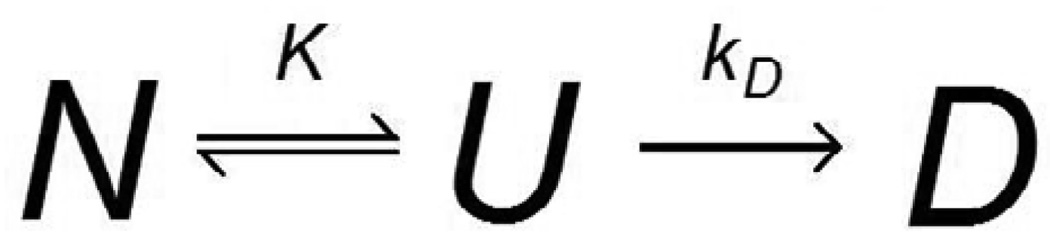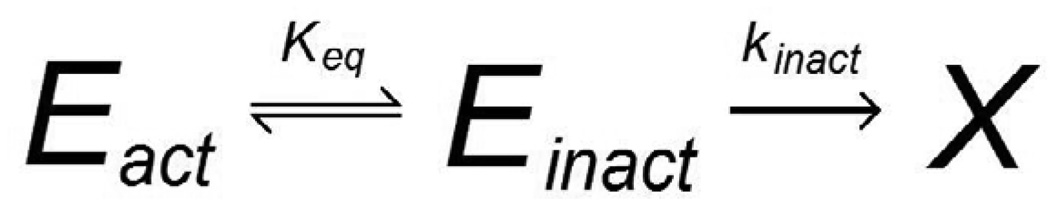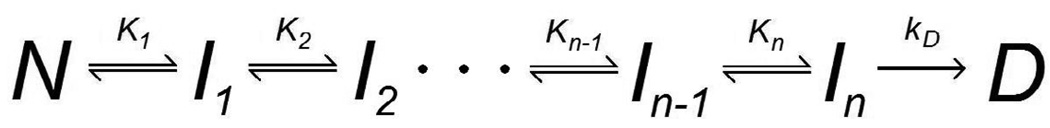Abstract
The expected product yield of a biocatalyst during its useful lifetime is an important consideration when designing a continuous biocatalytic process. One important indicator of lifetime biocatalyst productivity is the dimensionless total turnover number (TTN). Here, a method is proposed for estimating the TTN of a given biocatalyst from readily-measured biochemical quantities, namely the specific activity and the deactivation half-life, measured under identical conditions. We demonstrate that this method may be applied to any enzyme whose thermal deactivation follows first-order kinetics, regardless of the number of unfolding intermediates, and that the TTN method circumvents the potential problems associated with measuring specific catalyst output when a portion of the enzyme is already unfolded. The TTN estimation was applied to several representative biocatalysts to demonstrate its applicability in identifying the most cost-effective catalyst from a pool of engineered mutants with similar activity and thermal stability.
Keywords: Biocatalysis, Biochemical Engineering, Catalyst Deactivation, Stability, Total Turnover Number, catalyst lifetime productivity
1. Introduction
Biocatalysts are often superior to conventional catalysts in terms of high specificity, enantioselectivity, and catalytic efficiency (Illanes, 1999; Tao et al., 2007; Gibbs et al., 2005). In addition, enzyme catalysts possess many environmentally-positive attributes such as their biodegradability and propensity to operate at moderate temperature and pH in aqueous systems (Robles-Medina et al., 2009; Ran et al., 2007; Tramper et al., 1996). As such, biocatalysts are of great interest, particularly in the pharmaceutical and specialty chemical industries where enzymes can often provide the needed level of product purity in relatively few process steps.
Despite all of these advantages, the use of biocatalysts remains somewhat limited on the industrial scale (Bommarius and Polizzi, 2006; Makart et al., 2006). In large part, this is due to the fact that enzymes, derived from biological sources, have evolved to function most efficiently in conditions resembling those found in biological systems. There are, of course, exceptions to this rule and researchers are increasingly able to impart stability to biocatalysts by learning from the amino acid sequences of enzymes which tolerate harsh conditions, or by adding compounds to the reaction mixture (Kazlauskas and Lutz, 2009; Vielle and Zeikus, 2001; Azevedo et al., 1999). Enzymes can be tailored to resist organic solvents as well as salts (Vázquez-Figueroa et al., 2008), but thermal stability is an especially important trait since elevated temperature leads to more favorable reaction kinetics in a wide variety of processes (Zale and Klibanov, 1983).
The choice of operating temperature in an enzyme-catalyzed process involves the consideration of two competing processes: the rise in catalytic activity with increased temperature according to the well-known Arrhenius rate law, and the loss of structural integrity at the enzyme’s active site due to thermally-induced conformational changes and/or protein unfolding (Yoshioka et al., 1991; Peterson et al., 2007). Operating a process at a temperature very near the melting temperature (Tm) of an enzyme generally results in maximal turnover number but also in rapid deactivation. Since the cost of the biocatalyst itself is often significant, along with the potential down-time required to frequently replace spent catalyst, this may be an unfavorable operating regime. On the other hand, operating at temperatures far below Tm may prolong the catalyst lifetime and reduce energy costs but could result in unreasonably low space-time yields. As demonstrated in the literature, the true optimum temperature for an enzyme may be well below that at which denaturation becomes apparent through short-term experiments (Polakovic and Vrabel, 1996; Rogers et al., 2009).
In many cases, the range of acceptable operating temperature may be dictated by process constraints and the biocatalyst must be engineered to operate within that range. The engineer may be confronted with a large library containing several variants with similar activity and stability at the desired temperature, and must decide which variant will be most cost-effective over its process lifetime. While traditional indicators of biocatalyst performance based on intrinsic enzyme properties such as the Vmax/KM ratio are often utilized, these overlook the features of the specific process. Therefore, an indicator such as the catalytic effectiveness, which incorporates the enzyme behavior over the entire course of the reaction, is likely more applicable (Fox and Clay, 2009). However, the total turnover number (TTN) is an even more meaningful indicator of the suitability of a biocatalyst in a given process, as it directly scales the product yield to the catalyst input which renders it especially useful in cost estimation. The TTN is a dimensionless number, defined as the ratio of moles of product generated divided by the moles of biocatalyst used in a reaction; an alternative definition is the number of catalytic events performed by one active site of one molecule of the enzyme during its lifespan. In a continuous process using soluble, polymer-bound transfer hydrogenation catalysts (“chemzymes”), the TTN has been estimated to be the quotient of the catalyst turnover number and the rate constant of spent catalyst replacement (Laue et al., 2001). The notion of scaling activity to catalyst loss, i.e. deactivation rate, to estimate TTN has been developed for enzymatic systems by incorporating protein stability models such as the Lumry-Eyring model (Gibbs et al., 2005). However, enzymes can lose catalytic activity before they undergo a global loss of secondary structure, i.e. unfolding, and as such the deactivation process may involve multiple stable intermediate states (Vanhove et al., 1995). Thus, the question of catalyst loss is relatively complicated in the case of enzymes and can depend on several thermodynamic equilibrium processes.
Here, it is demonstrated that the TTN of a biocatalyst in a continuous, isothermal process can be estimated by performing two simple biochemical measurements. These measurements, the observed catalytic constant (kcat,obs) and the observed deactivation rate constant (kd,obs), take into account the operating conditions of the actual process and do not require a detailed knowledge of the enzyme’s deactivation mechanism. Assuming only that thermal deactivation of all active and intermediate forms of the enzyme proceeds via first-order kinetics, it is shown that regardless of the number of steps in the unfolding process, the TTN is simply the quotient kcat,obs/kd,obs when both values are measured at the chosen process temperature. These data are readily measured with common laboratory instrumentation and eliminate the potential problem of errant activity readings which ignore the fact that all of the enzyme in the initial sample may not be in its native (active) state.
2. Methods
2.1 Observed enzyme activity in an isothermal process
An enzyme will only exhibit catalytic activity when its native conformation is preserved. The maximum catalytic output is achieved when the enzyme is continuously kept saturated with substrate during its lifetime, i.e. when operating conditions are such that substrate concentration ≫ KM of enzyme at all times. Under saturated conditions, the instantaneous reaction rate Vmax is given by Equation 1, where [N] is the concentration of native (active) enzyme present.
| (1) |
The specific turnover number of the enzyme, kcat, is a function of temperature which can be defined according to thermodynamic transition state theory, as seen in Equation 2, where kB = Boltzmann constant, h = Planck’s constant, and R = gas constant. In an isothermal process, the value of kcat remains constant and depends only on the intrinsic activation parameter ΔGcat, the change in Gibbs free energy associated with activation of the enzyme-catalyzed reaction. Thus, for a given enzyme in an isothermal process, the observed Vmax depends only on one quantity which is variable with respect to time: the concentration of enzyme [N] which is still in its native state. Furthermore, the expression for the observed reaction rate may be written with time as the only variable, as shown in Equation 3, where kcat is taken to remain constant for the duration of the isothermal process. Therefore, to calculate product yield over the course of the process, it is necessary to obtain an expression for [N](t).
| (2) |
| (3) |
2.2 Generalizable model for long-term enzyme deactivation
Upon exposure to a denaturing condition such as a chemical denaturant or heat, an enzyme loses its native conformation and is rendered inactive, at least temporarily. Removal from the denaturing condition can result in the partial recovery of catalytic activity, but if the inactivated enzyme is held under the denaturing condition for a sufficiently long time it will become permanently and irreversibly denatured (Machado and Saraiva, 2005). The well-known Lumry-Eyring model of protein stability, shown in Scheme 1, treats enzyme denaturation as a two-step process: first, equilibrium between the native and unfolded conformations of the enzyme, designated N and U, respectively (the equilibrium constant K = [U]/[N]), and second, a first-order permanent denaturation (with rate constant kD) of the unfolded enzyme to a final state D (Lumry and Eyring 1954). More recent deactivation models, such as the Equilibrium Model recognize that, in general, any conformational change which compromises the integrity of the active site of the enzyme will cause catalytic activity to cease, whether or not this conformational change corresponds to the unfolding of the enzyme, i.e. loss of secondary structure (Peterson et al., 2007; Rogers et al., 2009). In such a case, an equilibrium is assumed between the native and inactive (though not necessarily unfolded) states. Scheme 2 shows the Equilibrium Model, in which Eact represents enzyme in its native conformation, Einact represents reversibly inactivated enzyme, and X is permanently denatured enzyme.
Scheme 1.
Lumry-Eyring Model (Lumry and Eyring 1954)
Scheme 2.
Equilibrium Model (Daniel et al., 2001)
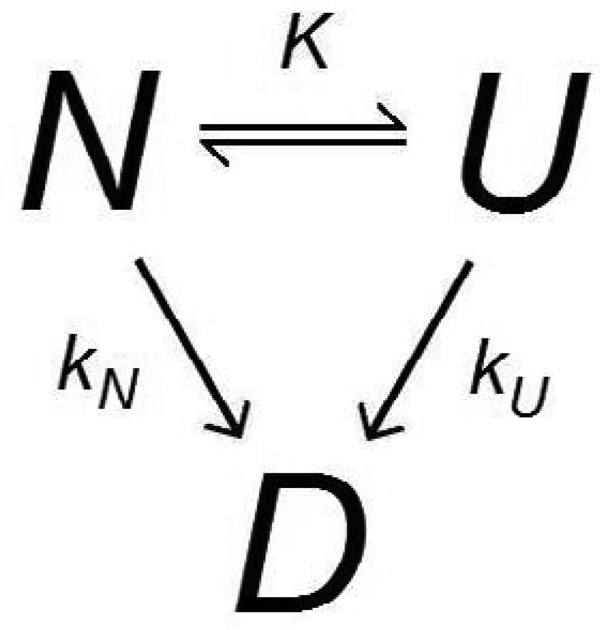
Both the Equilibrium Model, which in practice is often applied to short-term enzyme deactivation data with assays on the order of several minutes (Daniel et al., 2001; Peterson et al., 2007), and the Lumry-Eyring model assume that an enzyme must reach the unfolded or inactive state before it may become permanently denatured. When modeling enzyme deactivation over relatively long time periods, it may be necessary to consider other denaturing events which are not preceded by equilibrium unfolding, otherwise the models may result in artificially high total turnover predictions by ignoring effects which are best observed during assays longer than a few minutes. Gibbs et al. (2005) have previously suggested an “Extended Lumry-Eyring” model which includes a direct path for first-order denaturation from the native state, as seen in Scheme 3.
Scheme 3.
Extended Lumry-Eyring Model (Gibbs et al., 2005)
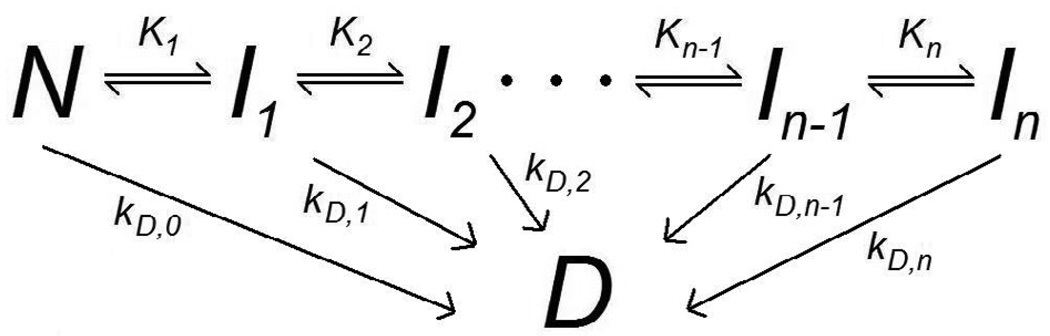
Another feature common to Scheme 1–Scheme 3 is that they model only one intermediate state between the native and permanently denatured states. Even though none of these models explicitly preclude the existence of additional unfolding intermediates, none are able to make a distinction between stable intermediates which have attained different degrees of unfolding. The existence of multiple unfolding equilibria would result in a deactivation model such as the one shown in Scheme 4, in which only the nth intermediate state, here represented as In, undergoes irreversible denaturation (Freire et al., 1990).
Scheme 4.
Multiple-Intermediate Model (Freire et al., 1990)
By combining the elements of Scheme 3 and Scheme 4, a generalizable theoretical model is proposed here which not only allows for multiple stable unfolding intermediates but also recognizes that each of these intermediates may proceed directly to a permanently denatured state, as shown in Scheme 5. For clarification, the use of a single state D in Scheme 5 is not an attempt to assert that all permanently denatured conformations which may be attained are identical, merely that they are all irreversible and nondescript, i.e. no longer considered to be species which participate in equilibria.
Scheme 5.
Multiple Intermediate Model with Direct Denaturation Pathways
2.3 Progress of enzyme deactivation during an isothermal process
By adopting the general deactivation model in Scheme 5, an expression can be derived for the amount of native enzyme remaining at any time during an isothermal process, i.e. the [N](t) term needed to complete Equation 3. The complete derivation of this term from the mass balance on all enzyme species and the thermodynamic definitions of the equilibrium constants and rate constants is shown in the Appendix. The result in terms of the model in Scheme 5 is shown in Equation 4.
| (4) |
In an isothermal deactivation experiment, the “observed” or apparent deactivation rate constant (kD,obs) resulting from the combination of all deactivation pathways will be equivalent to the exponential term of Equation 4, which may then be written more concisely as Equation 5. Substitution of this result into Equation 3 gives the desired expression for Vmax as a function of time, as shown in Equation 6.
| (5) |
| (6) |
The entire pre-exponential of Equation 6, except for [E]0, is equivalent to the “observed” or apparent kcat in an isothermal experiment. Assuming that all equilibria between the native state and the n intermediate states are established very rapidly, the kcat observed by instrumentation will be necessarily lower than the intrinsic kcat since some of the enzyme sample has already been rendered inactive and the activity calculation must be corrected by this factor. Hence, the final expression for instantaneous reaction rate as a function of time is given in Equation 7.
| (7) |
3. Results and Discussion
3.1 Total turnover number (TTN) expression from stability model
The process yield during the lifetime of a biocatalyst is equivalent to the integral of the instantaneous rate (Vmax) with respect to time, from zero to infinity (Equation 8). The expression for yield is obtained directly from the result of Equation 8, in which the non-varying terms kcat and [E]0 may be taken outside the integral (Equation 9). The integrated solution for overall yield is shown in Equation 10. The solution is then transformed to the dimensionless total turnover number after dividing by the concentration of biocatalyst initially present (specific yield per mole of catalyst). The final expression for TTN is shown in Equation 11.
| (8) |
| (9) |
| (10) |
| (11) |
3.2 Estimation of TTN from Activity and Deactivation Data
To obtain an idea about the order of magnitude of TTN for stable biocatalysts, the result of Equation 11 was applied to an assortment of different biocatalysts which exhibit first-order deactivation behavior, and for which both activity and deactivation data were available at the same temperature and buffer/substrate system. The first requirement for the application of this method is a first-order deactivation rate constant at the desired process temperature. Frequently, published first-order deactivation data are expressed in terms of a half-life, from which the rate constant can easily be extracted. The second requirement is the apparent turnover number (kcat,obs) measured at the same temperature as the deactivation data. In cases where the apparent value of kcat is not given explicitly in the literature, it can be calculated from the more prevalent specific activity data (U/mg) provided that the molecular weight of the enzyme per active site, or alternatively the overall molecular weight and number of active sites per enzyme molecule, is known. Equations 12 and 13 give the conversion formulas to derive kcat,obs from specific activity (U/mg) and kd,obs from half-life (converted to seconds).
| (12) |
| (13) |
Half-life and specific activity are indeed two of the most important parameters which characterize the thermal stability of an enzyme, and are thus available for a wide variety of biocatalysts; however, it is important to stress that the data must be obtained under the same conditions of temperature, pH value, and buffer content. Table 1 shows estimates of TTN for several biocatalysts which have been calculated according to Equation 11.
Table 1.
TTN estimates for several representative biocatalysts
| Enzyme (organism) | Substrate | Temp. (°C) |
kcat,obs (s−1) |
half-life (hr) |
kd,obs (s−1) |
TTN | Source |
|---|---|---|---|---|---|---|---|
| enoate reductase (Yersinia bercovieri) |
2-cyclo -hexenone |
45 | 4.5 | 1.95 | 9.87 × 10−5 | 4.56 × 104 | Chaparro-Riggers et al. (2007) |
| β-glucosidase (Pyrococcus furiosus) |
GlcpβNp[1] | 100 | 10.8 | 85 | 2.26 × 10−6 | 4.77 × 106 | Kengen et al. (1993) |
| glucose dehydrogenase (Sulfolobus solfataricus) |
D-glucose | 70 | 74.9 | 45 | 4.28 × 10−6 | 1.75 × 107 | [2] |
| subtilisin S41 (Antarctic Bacillus TA41) |
s-AAPF-pNa[3] | 60 | 264 | 0.16 | 1.24 × 10−3 | 2.13 × 105 | Miyazaki et al. (2000) |
| subtilisin 3-2G7 (Antarctic Bacillus TA41) |
60 | 553 | 9.43 | 2.04 × 10−5 | 2.71 × 107 | ||
| cephalosporin acylase CA130 wild-type (Pseudomonas sp.) |
GL-7-ACA[4] | 37 | 12.3 | 68.1 | 2.83 × 10−6 | 4.34 × 106 | Zhang et al. (2005) |
| cephalosporin acylase CA130-R121βA mutant (Pseudomonas sp.) |
37 | 12.2 | 88.3 | 2.18 × 10−6 | 5.59 × 106 | ||
| cephalosporin acylase CA130-K198βA mutant (Pseudomonas sp.) |
37 | 11.7 | 107.5 | 1.79 × 10−6 | 6.54 × 106 | ||
| cephalosporin acylase CA130-D286βA mutant (Pseudomonas sp.) |
37 | 12.7 | 53.9 | 3.57× 10−6 | 3.56 × 106 | ||
| glucose dehydrogenase strain 168 wild-type (Bacillus subtilis) |
D-glucose | 25 | 40.6 | 0.37 | 5.25 × 10−4 | 7.73 × 104 | Vazquez-Figueroa et al. (2007) |
| glucose dehydrogenase A246V mutant (Bacillus subtilis) |
25 | 51.8 | 0.31 | 6.08 × 10−4 | 8.52 × 104 | ||
| glucose dehydrogenase P105S mutant (Bacillus subtilis) |
25 | 6.1 | 0.52 | 3.73 × 10−4 | 1.64 × 104 | ||
| glucose dehydrogenase V227A mutant (Bacillus subtilis) |
25 | 33.1 | 0.67 | 2.89 × 10−4 | 1.15 × 105 |
p-nitrophenyl-b-D-glucopyranoside
Activity data from Lamble et al., 2003; half-life data from Giardina et al., 1986.
succinyl-LAla-LAla-LPro-LPhe-p-nitroanilide
glutaryl 7-aminocephalosporanic acid
The TTN, which itself is a dimensionless quantity, in each case corresponds to the expected yield in moles of product per mole of catalyst over the enzyme’s lifetime. Not surprisingly, the β-glucosidase and the glucose dehydrogenase from Sulfolobus solfataricus, which are industrial-grade catalysts derived from thermophilic organisms for their high thermal stability, exhibit relatively high TTN (on the order of 1–10 million). The data for subtilisin S41 illustrate how the engineered improvements to activity and stability translate into overall productivity; between the wild-type S41 and the improved variant 3-2G7 the specific activity was improved by a factor of 2.1 and the half-life increased by a factor of 59. Per the TTN estimation, the improved biocatalyst can be expected to yield approximately 127 times more product than the S41 over its lifetime. The utility of Equation 11 in selecting the best candidate catalyst for a given process from a pool of similar mutants can be seen in the data for cephalosporin acylase. Compared to the CA130 wild-type, the R121βA mutant has nearly the same specific activity but a longer half-life, and as expected exhibits a higher TTN. The D286βA mutant, compared to wild-type, shows a very slight (3%) increase in activity but a 21% shorter half-life, and accordingly can be expected to have an 18% lower TTN. The K198βA mutant, though it has 5% lower activity than the wild-type, has a 58% longer half-life. This translates into a 50% higher TTN and thus makes it the most productive variant for the given substrate at a process temperature of 37°C. A similar pattern is seen in the data for the glucose dehydrogenase strain 168, from Bacillus subtilis, and its mutants. The A246V mutant illustrates that in some cases one property (activity) may be increased at the expense of another (half-life) and result in an improved TTN, while the P105S mutant shows that this will not always be the case. The V227A mutant, though 19% less active than the wild-type, has an 80% longer half-life; the combination translates into a TTN which is 49% higher than that of the wild-type.
3.3 Strengths and Limitations of the TTN Method
The TTN captures the amount of product synthesized per amount of enzyme expended. As such, and with the assumption that prices for both product and biocatalyst are known, the contribution of the biocatalyst to the overall variable costs of production can easily be determined. At that point already, such a determination results in one of three situations: i) the cost contribution of the biocatalyst is negligible (no further work required), ii) the cost contribution of the biocatalyst is overwhelming, maybe more than the price of the product (different biocatalyst or process is required), or iii) the cost contribution is neither negligible nor overwhelming, i.e. acceptable but can often be improved. The method allows straightforward comparison between different biocatalysts. As such, TTN is one of the most important criteria for process development.
The TTN estimation should not be employed as the sole criterion for process suitability because biocatalysts can exhibit very large TTN at temperatures well below their optimum operating range. One study concluded that TTN of a given enzyme continues to increase as temperature is decreased due to the extended lifetime of the enzyme - however these yields could not be achieved in a practical sense, i.e. without unreasonably long residence times (Gibbs et al., 2005). Therefore, the TTN should also not be used as a tool for deciding the best operating temperature for the enzyme, as this will invariably be the lowest available temperature. Rather, the TTN method is highly applicable when an approximate design temperature is already known and several catalysts must be compared to decide which one is the best performer at that temperature. Another limitation of the TTN method is the assumption that all deactivation pathways obey first-order kinetics. In real processes, many effects such as protein aggregation may lead to loss of catalytic activity, and these may not always follow first-order rate laws. The inclusion of kcat,obs as a parameter also introduces some potential for inaccuracy. At higher operating temperatures where denaturation is relatively rapid, it may become increasingly difficult to capture the true initial enzyme activity in a conventional assay. A trade-off may occur in which the assay must be short enough in duration to exclude the time-dependent effects of denaturation but long enough to capture enough data points for a good fit and an acceptable signal-to-noise ratio from the instrumentation. It should also be noted that the isothermal experiments to determine kd,obs in cases where no literature exists, though very simple in design, may still need to span days or weeks especially in the case of industrially useful enzymes. An accelerated non-isothermal method for determining the TTN may be preferable in such cases (Gibbs et al., 2005).
The primary advantage of the TTN method is that it uses two quantities which are easily observed with common laboratory instrumentation, if not already available in the literature. Both the kcat,obs and kd,obs are easily extracted from specific activity and half-life data, respectively, which are widely published for a large number of biocatalysts. Another advantage of this method over some others which track the enzyme behavior through the course of an entire scaled-down reaction is that here the necessary parameters may be measured in discontinuous batch experiments, which involves less experimental labor, smaller quantities of substrate, and potentially lower costs.
4. Conclusions
A method has been presented for estimating the total turnover number (TTN), a dimensionless number which expresses the total moles of product yield per mole of biocatalyst during its operational lifetime. The TTN indicates the number of catalytic turnovers per active site over the whoole biocatalyst lifetime. The quantity for a biocatalyst at a given temperature of interest can be calculated as the quotient of the kcat,obs (apparent turnover number) and the kd,obs (first-order deactivation rate constant), both measured at the same temperature. Many biocatalysts have been characterized in terms of specific activity and half-life, from which kcat,obs and kd,obs are easily derived. The TTN method assumes minimal prior knowledge of the enzyme’s deactivation pathway; it holds true for enzymes with any number of intermediate unfolding states provided that all inactive intermediates become permanently denatured via first-order kinetics. This method has been shown to be effective in distinguishing the most suitable catalyst from a group of candidates with similar characteristics, though it should not be used as a method for determining an enzyme’s optimum operating temperature. The TTN method may be extended to any biocatalyst which fits an apparent first-order denaturation profile and has an established activity assay method at the desired process temperature. This method allows the enzyme engineer to quickly, and with minimal experimental data, estimate the cost contribution of biocatalyst to the variable process costs and to select the most cost-efficient candidate from a group of engineered catalysts with similar activity and stability.
Acknowledgments
T.A.R. gratefully acknowledges support from the National Institute of Health (Grant #5R01AI064817-02) and the GAANN (Graduate Assistance in Areas of National Need) Fellowship.
Appendix
Shown below is the complete derivation for [N](t), the concentration of native, active enzyme remaining at time t during an isothermal process, based on the deactivation model in Scheme 5. Firstly, a mass balance is performed on all enzyme species that occupy any of the different conformations including a number n of stable intermediates. Assuming a closed system with constant volume, the mass balance takes the form of Equation A1, where [E]0 is the initial concentration of enzyme in the system. Next, the definitions of the equilibrium constants are applied to the mass balance. The concentration of each of the intermediate states may then be written in terms of [N]. For example, since K1 = [I1]/[N] such that [I1] = K1[N] and furthermore K2 = [I2]/[I1] such that [I2] = K2[I1] = K1K2[N], the mass balance can be rewritten as Equation A2 and then factored as in Equation A3. The resulting expression is then condensed using summation notation according to Equation A4.
| (A1) |
| (A2) |
| (A3) |
| (A4) |
Each of the equilibria is treated as a van’t Hoff relationship in which the equilibrium constant Kn depends on temperature as well as the parameters Tn (the temperature at which [In]/[In−1] equals unity) and ΔHn (the enthalpy change associated with the transition from In−1 to In). The van’t Hoff relationship is shown in Equation A5, where R is the gas constant. It is hereby assumed that at the initial time t = 0, the equilibria between the native and intermediate states are rapidly (essentially instantaneously) established and that none of the enzyme has yet decayed to a denatured state. This leads to the initial condition shown in Equation A6.
| (A5) |
| (A6) |
To establish the time dependence of [N], Equation A4 is differentiated with respect to time as shown in Equation A7. Since all equilibrium constants are functions of temperature according to the van’t Hoff relationship and should not vary with time in an isothermal process, they need not be differentiated.
| (A7) |
The rate of accumulation of denatured enzyme is then assumed to equal the sum of the contributions from all native and intermediate states (which is valid if all pathways to D in Scheme 5 obey first-order kinetics). Each of the first-order decay processes is assumed to have a rate constant kD,n which may be modeled by thermodynamic transition state theory as in Equation A8. Here, kB = Boltzmann constant, h = Planck’s constant, R = gas constant, and ΔGn is the Gibbs free enthalpy change upon In transitioning to a denatured state. These deactivation rate constants, which are functions of temperature, are assumed to remain constant for the duration of an isothermal process.
| (A8) |
The total rate of accumulation is shown in Equation A9 which can be put in terms of [N] by again applying the definitions of the equilibrium constants, leading to Equation A10. Summation notation is then used to condense the expression according to Equation A12.
| (A9) |
| (A10) |
| (A11) |
| (A12) |
Equations A7 and A12 are combined to form Equation A13, and rearrangement yields the first-order differential equation in Equation A14. Since the coefficient is a constant under isothermal conditions, the system may be solved via separation of variables using the initial condition already set forth in Equation A6. The particular solution is therefore given by Equation A15.
| (A13) |
| (A14) |
| (A15) |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Azevedo AM, Fonseca LP, Prazeres DMF. Stability and stabilization of penicillin acylase. Journal of Chemical Technology and Biotechnology. 1999;74(11):1110–1116. [Google Scholar]
- Bommarius AS, Polizzi KM. Novel biocatalysts: Recent developments. Chemical Engineering Science. 2006;61(3):1004–1016. [Google Scholar]
- Chaparro-Riggers JF, Rogers TA, Vazquez-Figueroa E, Polizzi KM, Bommarius AS. Comparison of Three Enoate Reductases and their Potential Use for Biotransformations. Advanced Synthesis and Catalysis. 2007;349(8–9):1521–1531. [Google Scholar]
- Fox RJ, Clay MD. Catalytic effectiveness, a measure of enzyme proficiency for industrial applications. Trends in Biotechnology. 2009;27(3):137–140. doi: 10.1016/j.tibtech.2008.12.001. [DOI] [PubMed] [Google Scholar]
- Freire E, Osdol WW, Mayorga OL, Sanchez-Ruiz JM. Calorimetrically Determined Dynamics of Complex Unfolding Transitions in Proteins. Annual Review of Biophysics and Biophysical Chemistry. 1990;19:159–188. doi: 10.1146/annurev.bb.19.060190.001111. [DOI] [PubMed] [Google Scholar]
- Giardina P, De Biasi M, De Rosa M, Gambacorta A, Buonocore V. Glucose dehydrogenase from the thermoacidophilic archaebacterium Sulfolobus solfataricus. The Biochemical Journal. 1986;239(3):517–522. doi: 10.1042/bj2390517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gibbs PR, Uehara CS, Neunert U, Bommarius AS. Accelerated Biocatalyst Stability Testing for Process Optimization. Biotechnology Progress. 2005;21(3):762–774. doi: 10.1021/bp049609k. [DOI] [PubMed] [Google Scholar]
- Illanes A. Stability of Biocatalysts. Electronic Journal of Biotechnology. 1999;2(1):1–9. [Google Scholar]
- Kazlauskas R, Lutz S. Engineering Enzymes by “Intelligent” Design. Current Opinion in Chemical Biology. 2009;13(1):1–2. doi: 10.1016/j.cbpa.2009.02.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kengen SWM, Luesink EJ, Stams AJM, Zehnder AJB. Purification and characterization of an extremely thermostable beta-glucosidase from the hyperthermophilic archaeon Pyrococcus furiosus. European Journal of Biochemistry. 1993;213(1):305–312. doi: 10.1111/j.1432-1033.1993.tb17763.x. [DOI] [PubMed] [Google Scholar]
- Lamble HJ, Heyer NI, Bull SD, Hough DW, Danson MJ. Metabolic Pathway Promiscuity in the Archaeon Sulfolobus solfataricus Revealed by Studies on Glucose Dehydrogenase and 2-keto-3-deoxygluconate Aldolase. Journal of Biological Chemistry. 2003;278(36):34066–34072. doi: 10.1074/jbc.M305818200. [DOI] [PubMed] [Google Scholar]
- Laue S, Greiner L, Woltinger J, Liese A. Continuous Application of Chemzymes in a Membrane Reactor: Asymmetric Transfer Hydrogenation of Acetophenone. Advanced Synthesis and Catalysis. 2001;343(6–7):711–720. [Google Scholar]
- Lumry R, Eyring H. Conformation changes of proteins. Journal of Physical Chemistry. 1954;58(2):110–120. [Google Scholar]
- Machado MF, Saraiva JM. Thermal stability and activity regain of horseradish peroxidase in aqueous mixtures of imadazolium-based ionic liquids. Biotechnology Letters. 2005;27(16):1233–1239. doi: 10.1007/s10529-005-0023-y. [DOI] [PubMed] [Google Scholar]
- Makart S, Bechtold M, Panke S. Towards preparative asymmetric synthesis of β-hydroxy-α-amino acids: l-allo-Threonine formation from glycine and acetaldehyde using recombinant GlyA. Journal of Biotechnology. 2007;130(4):402–410. doi: 10.1016/j.jbiotec.2007.05.008. [DOI] [PubMed] [Google Scholar]
- Miyazaki K, Wintrode PL, Grayling RA, Rubingh DN, Arnold FH. Directed Evolution Study of Temperature Adaptation in a Psychrophilic Enzyme. Journal of Molecular Biology. 2000;297(4):1015–1026. doi: 10.1006/jmbi.2000.3612. [DOI] [PubMed] [Google Scholar]
- Peterson ME, Daniel RM, Danson MJ, Eisenthal R. The dependence of enzyme activity on temperature: determination and validation of parameters. Biochemical Journal. 2007;402(2):331–337. doi: 10.1042/BJ20061143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polakovic M, Vrabel P. Analysis of the Mechanism and Kinetics of Thermal Inactivation of Enzymes: Critical Assessment of Isothermal Inactivation Experiments. Process Biochemistry. 1996;31(8):787–800. [Google Scholar]
- Ran N, Zhao L, Chen Z, Tao J. Recent applications of biocatalysis in developing green chemistry for chemical synthesis at the industrial scale. Green Chemistry. 2008;10(4):361–372. [Google Scholar]
- Robles-Medina A, Gonzalez-Moreno PA, Esteban-Cerdan L, Molina-Grima E. Biocatalysis: Towards even greener biodiesel production. Biotechnology Advances. 2009;27(4):398–408. doi: 10.1016/j.biotechadv.2008.10.008. [DOI] [PubMed] [Google Scholar]
- Rogers TA, Daniel RM, Bommarius AS. Deactivation of TEM-1 beta-Lactamase Investigated by Isothermal Batch and Non-Isothermal Continuous Enzyme Membrane Reactor Methods. ChemCatChem. 2009;1(1):131–137. doi: 10.1002/cctc.200900120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao J, Zhao L, Ran N. Recent Advances in Developing Chemoenzymatic Processes for Active Pharmaceutical Ingredients. Organic Process Research & Development. 2007;11(2):259–267. [Google Scholar]
- Tramper J. Chemical versus Biochemical Conversion: When and How to Use Biocatalysts. Biotechnology and Bioengineering. 1996;52(2):290–295. doi: 10.1002/(SICI)1097-0290(19961020)52:2<290::AID-BIT8>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- Vanhove M, Raquet X, Frere JM. Investigation of the folding pathway of the TEM-1 beta-lactamase. Proteins: Structure Function and Genetics. 1995;22(2):110–118. doi: 10.1002/prot.340220204. [DOI] [PubMed] [Google Scholar]
- Vazquez-Figueroa E, Chaparro-Riggers J, Bommarius AS. Development of a Thermostable Glucose Dehydrogenase by a Structure-Guided Consensus Concept. ChemBioChem. 2007;8(18):2295–2301. doi: 10.1002/cbic.200700500. [DOI] [PubMed] [Google Scholar]
- Vázquez-Figueroa E, Yeh V, Broering JM, Chaparro-Riggers JF, Bommarius AS. Thermostable Variants Constructed via the Structure-guided Consensus Method also Show Increased Stability in Salt Solutions and Homogeneous Aqueous-Organic Media. Protein Eng. Des. Sel. 2008;21:673–680. doi: 10.1093/protein/gzn048. [DOI] [PubMed] [Google Scholar]
- Vieille C, Zeikus GJ. Hyperthermophilic Enzymes: Sources, Uses, and Molecular Mechanisms for Thermostability. Microbiology and Molecular Biology Reviews. 2001;65(1):1–43. doi: 10.1128/MMBR.65.1.1-43.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshioka S, Izutsu K, Aso Y, Takeda Y. Inactivation kinetics of enzyme pharmaceuticals in aqueous solution. Pharmaceutical Research. 1991;8(4):480–484. doi: 10.1023/a:1015899011324. [DOI] [PubMed] [Google Scholar]
- Zale SE, Klibanov AM. On the Role of Reversible Denaturation (Unfolding) in the Irreversible Thermal Inactivation of Enzymes. Biotechnology and Bioengineering. 1983;25(9):2221–2230. doi: 10.1002/bit.260250908. [DOI] [PubMed] [Google Scholar]
- Zhang W, Liu Y, Zheng H, Yang S, Jiang W. Improving the Activity and Stability of GL-7-ACA Acylase CA130 by Site-Directed Mutagenesis. Applied and Environmental Microbiology. 2005;71(9):5290–5296. doi: 10.1128/AEM.71.9.5290-5296.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]