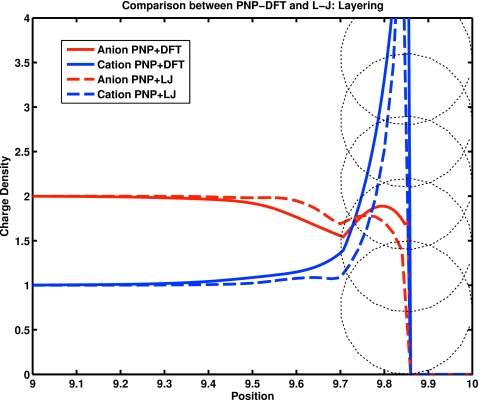
Figure 1.

The number density (“concentration”) of ions near a charged wall. The wall has charge density of 0.1 C∕m². Charge is shown divided by 1 C∕m³. The diameter of the ions is 0.3 nm and they have charges of +2e and −1e, where e is the charge on a proton. Position is shown divided by nanometer. Dielectric coefficient was 78, temperature was 298 K, and the bulk concentration of ions was 1 M of the divalent cation and 2 M of the monovalent anion. The potential on the wall was set to −3.1 kT∕e, i.e., −80 mV in accord with MC simulations (Ref. ²⁰²). Energy coupling coefficients λ in EnVarA were 0.5. The dotted circles show the size of the ions in the calculation. Ions are not allowed to overlap with the wall and so the densities are smooth functions until they reach the excluded zone produced by finite diameter of the ions. Calculations were done using (solid lines) the PNP-DFT and PNP-LJ in the form described in the text and Appendixes A, C. The form of the DFT differs in detail (but not spirit) from that in recent literature (Refs. ⁶⁷, ⁶⁸, ²⁰³): we use DFT for uncharged interactions (following Refs. ⁶⁶, ¹⁴², ²⁰⁴) but we use EnVarA to deal with the electrostatics. EnVarA identically satisfies Gauss’ law (which is also one of the sum rules (Ref. ⁷² of statistical mechanics). This calculation is called PNP-DFT even though we report only equilibrium results: the variational method knows nothing of equilibrium and always computes a nonequilibrium transient response which may in special cases have no flows and a stationary solution. The results are qualitatively similar to the layering reported in MC simulations (Ref. ¹³²). Quantitative differences are expected because the systems are not identical. Most importantly, simulations were of hard spheres (whereas we use Lennard-Jones or DFT in one dimension). There are many other small differences; e.g., MC uses an approximation to the solution of Poisson’s equation (Ref. ²⁰⁵) that produces results independent of system size, but without definite error bounds (Refs. ¹³⁵, ²⁰⁶).