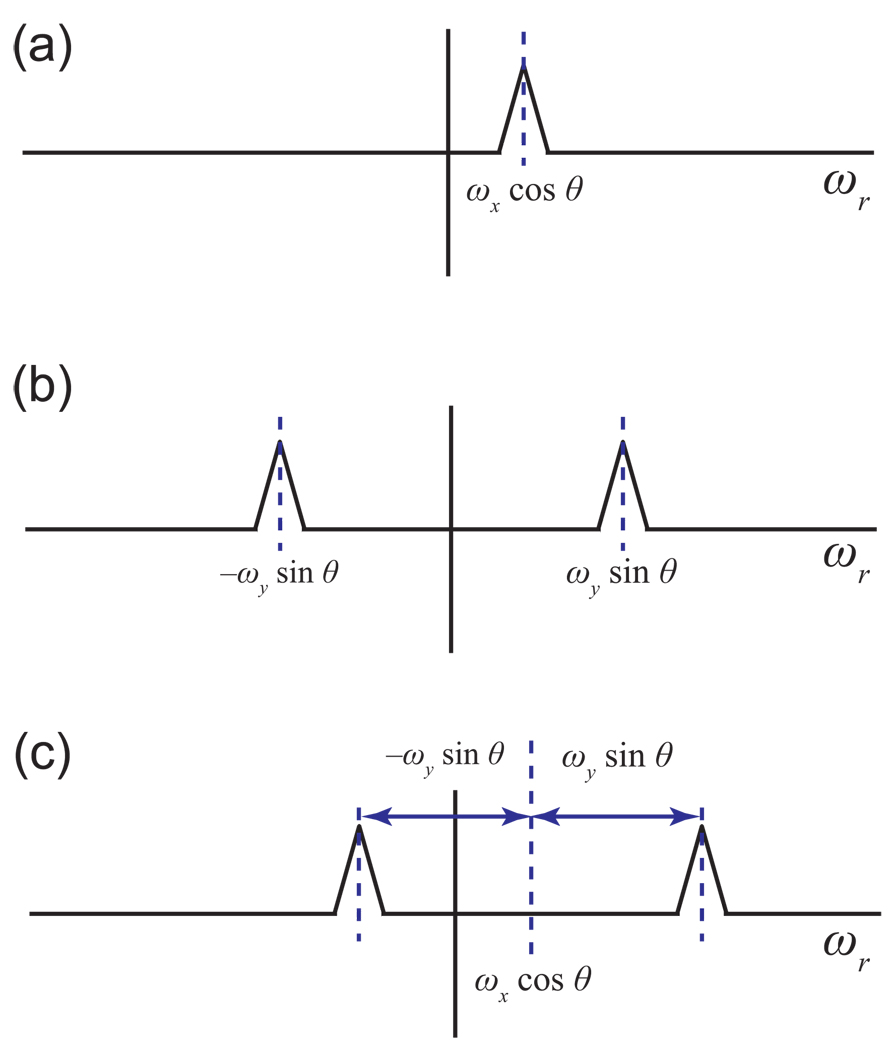
Figure 11. Radial Spoke Peak Positions in the Absence of Full Quadrature Detection.

Fourier transformation of a radial spoke measured with quadrature information for only one dimension leads to a frequency domain multiplet. That can be understood by the convolution argument, shown here for the example of a slice at angle θ through a 2-D time domain, with quadrature detection in x and real detection in y. (a) Because complex data are available for x, a radial slice of the x signal alone would show as a single peak at the position ω_x cos θ. (b) Since imaginary components are not available for the y signal, the Fourier transform of a slice of it alone would show a doublet. (c) The actual time domain observation is the product of the x and y signals, yielding a convolution of (a) and (b) in the frequency domain. The result is a doublet centered on the scaled x frequency, with a splitting equal to twice the scaled y frequency.