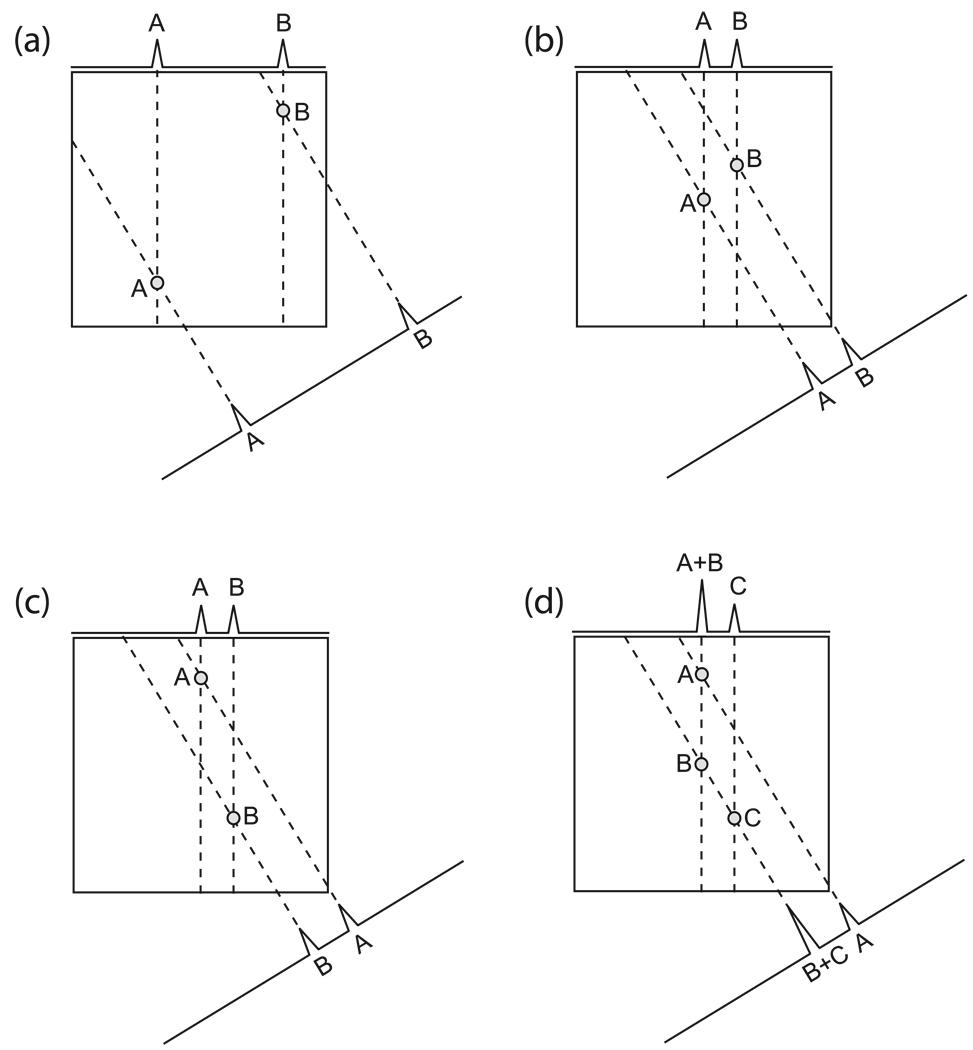
Figure 13. Identification of Multidimensional Signal Positions from Projections When Multiple Signals are Present.

(a) Two peaks are present on each of these two projections (one projection parallel to x, and the other at an angle of 30° to x). By extending lines back across the 2-D space of interest from the projected peaks, one can determine the locations of the original signals, which are found where the backprojection lines intersect. In this case, there are only two possible intersection points for the backprojection vectors within the spectral region, meaning that the original positions of the two peaks can be identified unambiguously. (b and c) In a less favorable case, there are two possible interpretations for the projection data, both equally likely. The original peaks could be located as in (b) or they could be located as in (c); these two configurations give identical projection data, and one needs additional information to resolve the ambiguity. Note that this ambiguity would plague any method trying to interpret this data, regardless of whether it is automatic or manual, and regardless of whether it attempts to reconstruct a spectrum or merely attempts to calculate frequencies from the projected peak positions. (d) The relative intensities of the projected peaks might provide a means for resolving ambiguities. In this case, one possible answer is that there are three peaks of equal height, A, B and C, positioned as shown. However, without additional information one could not exclude another possibility, namely a configuration like that of (b), but with a peak A twice as strong as B.