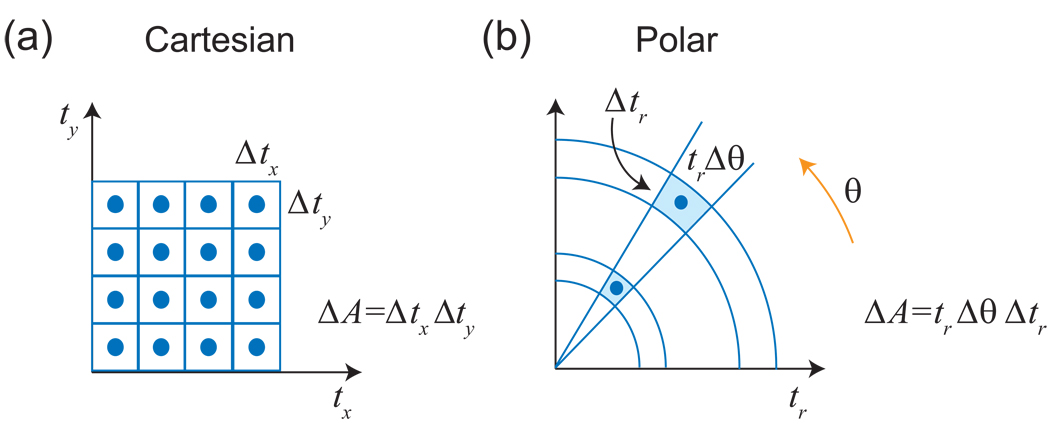
Figure 16. Weighting of Data Points in the Polar Fourier Transform.
(a) With conventional grid sampling, the area occupied by each sampling point, ΔA, is the same, and no special weighting is required during the Fourier transform. (b) In polar coordinates, sampling points that are closer to the origin are spaced more closely together. To correct for this, one must weight the points during the Fourier transform according to their area, ΔA. The appropriate weighting factor for 2-D is tr, the distance from the origin. Note that this weighting factor is identical to the filter function used in filtered backprojection.