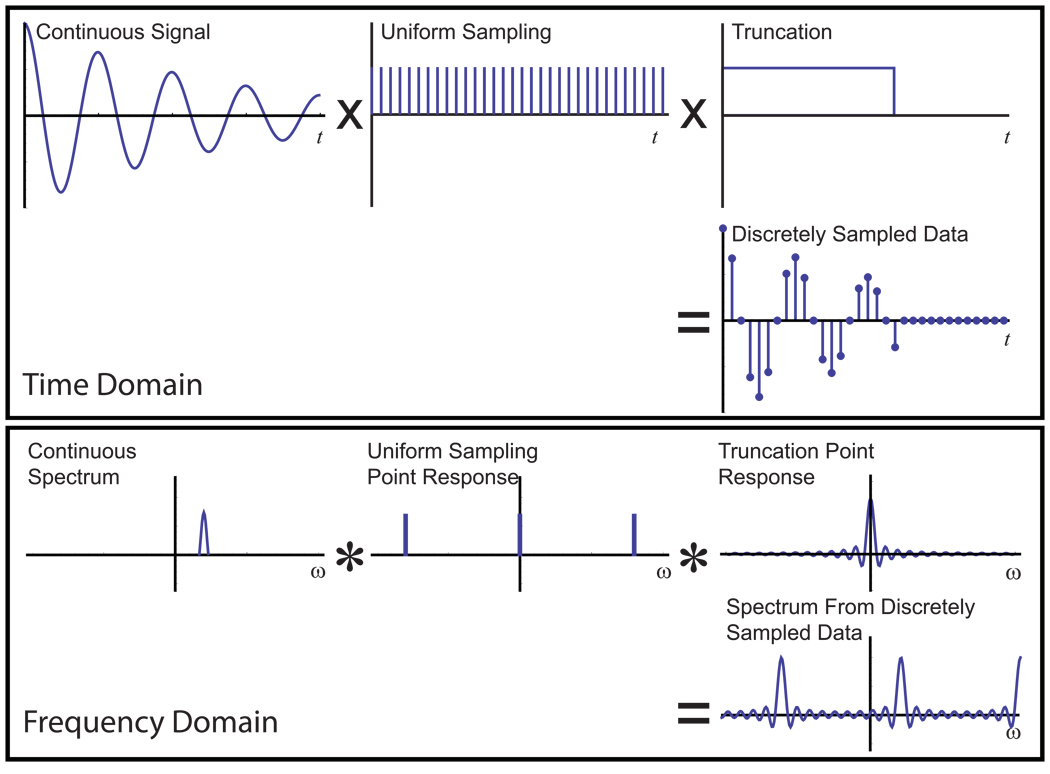
Figure 3. Point Responses, Convolution and Discrete Sampling.

The consequences of discretely sampling a continuous signal can be understood through the convolution theorem of the Fourier transform. In the time domain, the sampling process can be written mathematically as a multiplication of the continuous signal with functions describing the sampling—in this case, one function specifying evenly distributed samples, and a second function specifying the limited duration of the sampling interval. Each of these sampling functions has a Fourier transform, shown below, which is called its point response. According to the convolution theorem, the effects of sampling in the frequency domain are described by convolving (in the commonly-accepted convention of Bracewell, indicated by the operator “*”) the continuous spectrum with the point responses from the two sampling functions, yielding the discrete spectrum, with its aliasing and truncation artifacts.