Table 3.

Test 1, summary of Tk-GV results showing no out-of-bounds, i.e., nonphysical, parameter values. Parameter values do not correspond in adjacent row cells!

	Parameters from Tk-GV fits								Jackknife LOOa
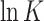
Percentile			α	β (min−1)	CL (ml/min)	V (ml)	s CL (ml/min)	s V (ml)	s CL (ml/min)	s V (ml)
0th	0	−5.364	0.5945	0.000106	1.242	7404	0.1876	63.02	0.1075	18.71
25th	0.01216	−4.537	0.7140	0.002169	44.39	13127	1.404	288.0	0.8542	200.6
50th	0.09308	−4.280	0.7749	0.003452	74.28	16275	2.510	474.5	1.696	384.8
75th	0.2610	−3.991	0.8649	0.004556	105.5	18490	3.703	690.6	2.708	531.9
100th	2.197	−3.386	0.9895	0.009080	157.6	31124	6.222	1344	10.51	1283
Probabilityb	<0.0001	0.970	0.158	0.123	0.162	0.166	0.116	0.113	<0.0001	0.004

The 46 patient studies parameters are listed in percentiles from smallest to largest case from fitting all 8 or occasionally 9 samples. Parameters for the fit equation 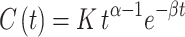were regressed by Tikhonov regularization with the dimensionless shrinkage factor, λ, a.k.a., the Tikhonov “smoothing” parameter. α is also dimensionles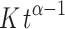s. has the units of concentration. The resulting plasma–clearance rates and volumes are CL and V. The standard deviations, s _CL and s _V are calculated by two independent methods. The first is directly from Tikhonov regularization of m samples, using the standard formula for propagation of small errors

^aThe second method uses jackknife of 373 leave one out (LOO) Tk-GV trials (m − 1 samples)

^bShapiro–Wilk probability is a method of testing for a Normal Distribution (ND). Note that lnK is an ND