Cation Charge Dependence of the Forces Driving DNA Assembly

Abstract

Understanding the strength and specificity of interactions among biologically important macromolecules that control cellular functions requires quantitative knowledge of intermolecular forces. Controlled DNA condensation and assembly are particularly critical for biology, with separate repulsive and attractive intermolecular forces determining the extent of DNA compaction. How these forces depend on the charge of the condensing ion has not been determined, but such knowledge is fundamental for understanding the basis of DNA-DNA interactions. Here, we measure DNA force-distance curves for a homologous set of arginine peptides. All forces are well fit as the sum of two exponentials with 2.4- and 4.8-Å decay lengths. The shorter-decay-length force is always repulsive, with an amplitude that varies slightly with length or charge. The longer-decay-length force varies strongly with cation charge, changing from repulsion with Arg¹ to attraction with Arg². Force curves for a series of homologous polyamines and the heterogeneous protein protamine are quite similar, demonstrating the universality of these forces for DNA assembly. Repulsive amplitudes of the shorter-decay-length force are species-dependent but nearly independent of charge within each species. A striking observation was that the attractive force amplitudes for all samples collapse to a single curve, varying linearly with the inverse of the cation charge.

Introduction

In nature, DNA primarily exists in a highly compact state. Understanding the physical basis of DNA packaging is a necessary first step toward elucidating how nature both generates and employs condensates to store and to protect genetic information in vivo. In bacteriophages, for example, DNA double helices are packed under high pressure with center-to-center helix separations of ∼27 Å (1,2). Eukaryotic genome compaction is mediated by packaging of DNA in chromatin. DNA helices wrapped around the histone core of nucleosomes are also separated by ∼27 Å, but stably (3). There is a further range of chromatin compactions from densely packed heterochromatin to more open regions associated with active gene expression. The transition among packing densities is paramount to regulation in the cell (4–6). During vertebrate spermiogenesis, chromatin is dramatically reorganized in developing spermatids. Histones are mostly replaced with protamines, arginine-rich peptides, to compact DNA even further for efficient genetic delivery (7–9). In sperm heads, DNA seems to be tightly packed into toroids (10).

Although in vivo packaging is primarily protein-mediated, it is also well known that small multivalent cations condense DNA effectively in vitro (11,12). Multiple examples of highly condensed in vitro packaging of DNA can be found in synthetic gene delivery vectors (13–16). DNA assembly by multivalent ions is a critical testing ground for understanding not only in vivo compaction of DNA but also the physics of interactions between charged molecules. In a sufficient concentration of multivalent ions, DNA will spontaneously assemble into an ordered array. The helices do not collapse to touching but rather are separated by 5–15 Å of solution, depending on the nature of the condensing ion. The observed equilibrium spacings represent a balance of the attractive and repulsive forces. The measured force characteristics, pushing in from the equilibrium spacing using osmotic stress, are remarkably similar for compact metal ions such as Co(NH₃)₆³⁺ and Mn²⁺, the oligoamines spermidine and spermine, with charge separations of 5–6 Å, and salmon protamine, a peptide 32 amino acids in length, suggesting a common set of forces for these very different cations (17–19).

The physical basis of the long-range forces in DNA self-assembly is still unresolved. Experimental studies (17–23) have aimed to elucidate the fundamental physical mechanisms responsible for DNA condensation. In vitro experiments have shown that DNA condensation from bulk solution critically depends on the valence of the counterions and that a charge of +3 or larger is usually required to overcome the inherently large electrostatic repulsive barrier between the like-charged polyelectrolytes (24,25), although a few divalent ions such as Mn²⁺ and Cd²⁺ are capable of condensing double-stranded DNA. As traditional theories of intermolecular forces have not proven sufficient to describe DNA intermolecular forces, new theories continue to be developed (26–31). Theoretical treatments of the interhelical force range from classical electrostatics in a continuum dielectric (26,28,30) to hydration interactions that emphasize the disruption of water structure in tight spaces (17,19,32). To predict attraction, most theories include some form of correlation, i.e., counterion charges on one helix appose the DNA phosphate charge on another. These counterion correlations may be induced by inter- or intrahelical charge interactions or may result from the natural tendency of counterions to bind to sites on the DNA that lead to attraction, as in the electrostatic zipper model (31,33,34). As depicted in Fig. 1, these theories predict that more highly correlated counterions result in greater attraction, thus resulting in tighter packaging of DNA.

Figure 1.

Schematic cartoon illustrating two possible correlation states for polycation placement on DNA. Most theories predict increased attraction in going from a less correlated (left) to a highly correlated state (right), leading to tighter DNA packaging.

There is a pressing need for more measurements of DNA-DNA intermolecular forces to elucidate fully the nature of the underlying forces, as well as to advance and discriminate among the alternate theories. In this article, we focus on the measurement of force versus separation between DNA helices in the presence of arginine and polyamine cations as a function of cation length or, equivalently, charge. Osmotic stress combined with x-ray diffraction allows us to directly measure thermodynamic forces between DNA helices in ordered assemblies. Building on the constraining results from previous combined osmotic stress and single-molecule tweezing experiments (19), we fit force curves to double exponentials, allowing for the direct separation of the attractive and repulsive contributions to the force-distance curves. Although intermolecular DNA-DNA forces depend on the specific nature of the cation, we show that for a given homologous cation series, the repulsive contributions are comparatively insensitive to cation charge. In contrast, attractions show a large dependence on cation charge N, varying linearly with 1/N.

Materials and Methods

Reagents

Dimethylamine ((CH₂)₃NH) hydrochloride, putrescine (NH₂(CH₂)₄NH₂) dihydrochloride, spermidine (H₂N(CH₂)₃NH(CH₂)₄NH₂) trihydrochloride (spd⁺³), L-arginine hydrochloride, and poly-L-arginine hydrochloride (P7662 15–70 kDa, molecular weight (MW) average ∼35,500) were obtained from Sigma-Aldrich (St. Louis, MO). Polyethylene glycols (PEG) of average molecular weight (MW) 8000 and 20,000 and spermine (H₂N(CH₂)₃NH(CH₂)₄NH(CH₂)₃NH₂) tetrahydrochloride (spm⁺⁴) were purchased from Fluka Chemical (Buchs, Switzerland). The arginine peptide series ranging from diarginine to hexaarginine were custom-synthesized and purified at >98% by GenScript Corporation (Piscataway, NJ). All chemicals were used without further purification. High-molecular-weight DNA was prepared and purified from adult-chicken whole blood as described previously (17) and dialyzed against 10 mM TrisCl (pH 7.5) and 1 mM EDTA.

Sample preparation

For mono and divalent species, precipitated DNA pellets (∼250 μg DNA) are prepared by precipitation with either ethanol or 5% PEG in appropriate salt solutions. Precipitates are equilibrated against PEG-salt bath solutions in vast excess at a known osmotic pressure. PEG is excluded from the DNA phase, thus exerting an osmotic pressure on the pellet while also allowing for the free interchange of water and small ions to equilibrate between the two phases. Pellets are typically equilibrated for 2 weeks, with several changes of the bathing PEG-salt solution.

For tri- and higher-valent cations, DNA spontaneously precipitates, and samples for x-ray scattering were prepared in several ways. Concentrated polycation solutions were added to ∼1 mg/mL chicken erythrocyte DNA (∼250 μg DNA) in 10 mM TrisCl (pH 7.5) in steps of 0.2 mM. Each addition was thoroughly mixed before adding more condensing ions and continued until all DNA was precipitated. Alternatively, condensing ions were added to DNA in a single aliquot to an equivalent final concentration. The resulting fibrous samples were centrifuged and transferred to corresponding PEG-salt solutions and allowed to equilibrate for ∼2 weeks. X-ray scattering profiles did not depend on the method used to prepare the DNA precipitate and did not change after 6 months. Osmotic pressures of the PEG-salt solutions were measured directly using a Vapro vapor pressure osmometer (5520, Wescor, Logan, UT).

Critical concentrations

The critical concentration of each condensing cation (e.g., spermidine or triarginine) for precipitation of DNA from dilute solution was determined as described in Pelta et al. (25). A series of DNA samples were prepared with varied cation concentration in Tris buffer. DNA concentration was ∼15 mM basepairs in 1 mL total volume. After incubation at room temperature for ∼1 h, the solution was centrifuged at ∼16,000 × g for 10 min and the DNA absorbance at 260 nm of the supernatant was measured. Critical concentrations were observed to decrease by approximately an order of magnitude for each additional charge. The cation concentration used in the polyethylene glycol (PEG) bathing solution for osmotic stress force measurements was two- to fourfold higher than the critical concentration. Over this range, the observed spacing between helices does not depend on cation concentration. The force curves for putrescine and diarginine are insensitive to the concentration of the divalent ion between 5 and 20 mM.

Osmotic stress

The method for direct force measurement by osmotic stress has been described previously (32). In brief, condensed DNA arrays are equilibrated against a bathing polymer solution, typically PEG, of known osmotic pressure. PEG is excluded from the condensed-DNA phase, applying a direct force on the condensate. Water, salt, and small solutes are freely exchanged between the PEG and condensed-DNA phases. Allowed to equilibrate, the osmotic pressure measurements in the two phases are identical. Using small-angle x-ray scattering (17–19), the interhelical spacing, D_int, is measured as a function of the applied osmotic pressure to obtain force-versus-separation curves.

X-ray scattering

Ni-filtered Cu-Kα radiation from an Enraf-Nonius Service (Bohemia, NY) fixed-copper-anode Diffractis 601 x-ray generator equipped with double focusing mirrors operated at 0.9 kW was used for small-angle x-ray scattering (SAXS) experiments. The primary beam was collimated by a set of slits. Samples were sealed with a bath of equilibrating solution in the sample cell and then mounted into a temperature-controlled holder at 20°C. The flight path between the sample and the detector was filled with helium. Diffraction patterns were recorded by direct exposure of Fujifilm (Tokyo, Japan) BAS image plates and digitized with a Fujifilm BAS 2500 scanner. The images were analyzed using the FIT2D and SigmaPlot 9.01 (SPSS, Chicago, IL) software programs. The distance from the sample to the image plate, calibrated using powdered p-bromobenzoic acid and silver behenate, was found to be ∼16.7 cm. In typical scattering experiments, we see not only the Bragg reflection, to determine interaxial DNA-DNA spacings, but also higher-order reflections typical of hexagonal packaging. The interaxial distance between hexagonally packed helices is D_int = $4\pi /3\times q_{100}$, where q₁₀₀ is the scattering vector, q, which corresponds to the maximum in the scattering. q is defined as q = (4π/λ)sinθ where 2θ is the scattering angle. For different samples equilibrated at the same PEG-salt conditions, D_int values are reproducible to within ∼0.1 Å. X-ray scattering patterns were reproducible over at least several months of storage. No sample degradation was apparent. Typical exposure times were of the order of 40 min.

Results

Fig. 2 A shows osmotic stress curves for a series of arginine peptides from the mono-amino acid (Arg₁) to hexaarginine (Arg₆) and polydisperse polyarginine (poly(Arg), average molecular mass ∼35 kDa, or ∼Arg₂₀₀). Arg₁-DNA forces are repulsive at all osmotic pressures. The force data for Arg₂-DNA show a transition from repulsion to attraction at low osmotic pressures, as seen previously for subcritical concentrations of Co(NH₃)₆³⁺ and for Mn²⁺. DNA will spontaneously assemble with +3 or higher-charge arginine peptides. The equilibrium spacing in the absence of applied osmotic pressure decreases with increasing arginine peptide charge. The figure inset shows expanded plots for the +3 and higher-charge arginine peptides.

Figure 2.

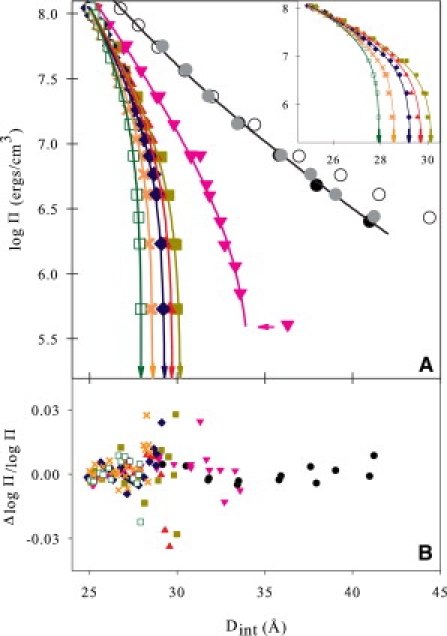
(A) The distance dependence of intermolecular DNA pressures measured by osmotic stress for a homologous arginine series: Arg₂ (inverted triangles), Arg₃ (solid squares), Arg₄ (triangles), Arg₅ (diamonds), Arg₆ (exes) and a 35-kDa poly-L-arginine, poly(Arg) (open squares). Three concentrations of Arg₁ are shown, 0.2 M (open circle), 1.2 M (gray circle) and 2 M (black circle). Arg₁ and Arg₂ do not spontaneously condense DNA. The solid lines are fits to Eq. 2 or 3 with λ = 4.8 Å. The 1.2- and 2-M Arg₁ data overlap and are well described by the double exponential; 0.2 M Arg₁ has an additional electrostatic contribution at low pressure but converges with the high Arg₁ concentration data at high osmotic pressures. Arg₂ shows weak attractions similar to those of higher-valency arginines but undergoes a phase transition at D_int > 34 Å at low Π. Cations with charge ≥+3 spontaneously condense DNA. Equilibrium interaxial spacings at Π = 0, D_eq, are indicated by arrows. (Inset) All of the condensed arginine measurements converge to the same curve at high pressures, indicating that the underlying repulsions are similar. (B) Error plots of ΔlogΠ/log Π = (logΠ_exp − logΠ_calc)/log Π_exp for all the fits in A are shown.

We fit these osmotic pressure, Π, versus spacing, D, curves to a double-exponential equation with variable preexponential factors A and R:

$$\Pi ={\Pi }_r+{\Pi }_a={\mathrm{Re}}^{-2D/\lambda }+A{e}^{-D/\lambda },$$ (1)

or, equivalently,

$$\log (\Pi )=\log \left(R\right)-\frac{2D}{2.303\lambda }+\log \left(1+\frac{A}{R}{e}^{D/\lambda }\right),$$ (2)

with the decay length, λ, fixed at 4.8 Å. This form is the result of recent work (19) in which osmotic stress measurements were combined with single-molecule magnetic-tweezer measurements to separate the attractive and repulsive free energies at the equilibrium spacing for several commonly used condensing agents. The results depend only weakly on the decay length, λ, over the range ∼+0.5 to −0.5 Å.

For cations that spontaneously assemble DNA, the coefficients R and A can be related through the equilibrium spacing, D_eq, since Π(D_eq) = 0, giving a fitting equation with only a single variable, R:

$$\log (\Pi )=\log \left(R\right)-\frac{2D}{2.303\lambda }+\log \left(1-e^{-\left(D_{eq}-D\right)/\lambda }\right).$$ (3)

The repulsive and attractive free-energy contributions (G_r and G_a, respectively) from the two individual forces per DNA phosphate at a spacing D can be calculated by integrating ΠdV for each exponential from ∞ to D, assuming hexagonal packing:

$$\frac{\Delta G_{\text{r}}\left(D\right)}{kT}=\frac{\sqrt{3}b\left(\lambda /2\right)\left(D+\lambda /2\right)}{kT}{\Pi }_{\text{r}}\left(D\right)$$ (4)

and

$$\frac{\Delta G_{\text{a}}\left(D\right)}{kT}=\frac{\sqrt{3}b\lambda \left(D+\lambda \right)}{kT}{\Pi }_{\text{a}}\left(D\right),$$ (5)

where b is the linear spacing between DNA charges, 1.7 Å/DNA phosphate.

The solid lines in Fig. 2 A are fits to Eq. 2 or 3. Force curves for 1.2 and 2 M ArgCl superimpose and are well fit by Eq. 2. The curve for 0.2 M ArgCl has an additional contribution from electrostatics at low pressures; the high-pressure data, however, superimpose with the high-salt-concentration data and fit. Arg₂ does not spontaneously condense DNA. We observe, however, a significant long-range attractive component. With low osmotic pressure, Arg₂-DNA is observed to form a liquid-crystalline-type packaging and undergoes a phase transition to a hexagonal phase at log(Π) ∼ 5.7 (Fig. 2 A, horizontal arrow). The best fit of the Arg₂ force data after the transition to Eq. 3 has D_eq = 34.4 Å. The fitting errors, ΔlogΠ/logΠ = (logΠ_exp − logΠ_calc)/logΠ_exp, for all the data shown are given in Fig. 2 B. No systematic deviations are observed.

Both a decreased repulsive force and an increased attraction could account for the decrease in D_eq as the number of arginine charges increases. Fig. 3 A shows the contribution to the osmotic pressure at 25 Å separation calculated from the 4.8-Å-decay-length force and the 2.4-Å-decay-length repulsion as a function of the number of arginine charges, N. The 2.4-Å-decay-length force amplitude increases by ∼40% from Arg₁ to Arg₆. The repulsive force amplitude for polyarginine is an additional ∼15% larger than for Arg₆. The 4.8-Å-decay-length force amplitude change is significantly larger while smoothly changing from repulsion to attraction. Thus, an increasing attractive force accounts for the decrease in D_eq. Fig. 3 B shows how the net ΔG/DNA phosphate, calculated using Eqs. 4 and 5, is dependent on equilibrium spacing for Arg₂ through polyarginine. Here, ΔG_net = −(ΔG_a(D_eq) + ΔG_r(D_eq)). As measured experimentally using magnetic tweezers (19), the energies associated with DNA compaction are quite small. Even for poly(Arg), the energy minimum is <0.5 kT/DNA charge.

Figure 3.

(A) Contributions to the osmotic pressure from forces with 2.4-Å (open circles) and 4.8-Å (solid circles) decay length at 25 Å DNA-DNA separation, calculated from the fits to the curves in Fig. 2A, are shown as a function of the number of arginine repeats. Note the change in scale between Arg₆ and poly(Arg). Amplitudes of the force with shorter decay length increase weakly with N (∼40%) from Arg₁ to Arg₆, but the change in amplitude is small compared with changes in the exponential force with longer decay length, which ranges from positive to negative values. (B) Depths of the free-energy minimum (ΔG_net)/DNA phosphate at the equilibrium spacing, D_eq, calculated from the double-exponential fits, are shown for Arg₂ through poly(Arg). The dashed line is drawn to guide the eye.

Similar force curves for polyamines were previously reported by Todd and Rau (19). Polyamines are ubiquitous small polycations that show a high affinity for DNA and have multiple functions in cell growth and differentiation (35–38). The force data for dimethylammonium (DMA)¹⁺, putrescine²⁺, spermidine³⁺, and spermine⁴⁺ are shown in Fig. 4. The solid lines are the best fits to Eq. 3 for the spermidine and spermine force data and to Eq. 2 for the 1.2- and 1.6-M DMA¹⁺ data. Only the 2.4-Å-decay-length force is apparent for putrescine²⁺ for log(Π) > 6.8; the 4.8-Å-decay-length force contribution is negligible. Force data for reconstituted salmon protamine-DNA assemblies is also shown in Fig. 4. The solid line is the best fit to Eq. 3 with λ = 4.8 Å. Salmon protamine is a small, arginine-rich (21 of 32 total amino acids) peptide used to package DNA in sperm heads. The equilibrium spacing or, equivalently, the DNA packaging efficiency for protamine is equivalent to Arg₅.

Figure 4.

DNA osmotic-stress force curves are shown for a homologous polyamine series: 1.2 (gray circles)- and 1.6-M (black circles) dimethylammonium (DMA¹⁺), putrescine (Put²⁺) (triangles), spermidine (Spd³⁺) (squares), spermine (Spm⁴⁺) (diamonds). The arginine-rich peptide salmon protamine chloride (inverted triangles) is also shown. Solid lines are fits of the data to Eq. 2 or 3 with λ = 4.8 Å. Put²⁺ has only the force with 2.4 Å decay length apparent at pressures >6.8. Neither DMA¹⁺ nor Put²⁺ spontaneously condenses the DNA. Spd³⁺ and Spm⁴⁺ spontaneously condense DNA.

Fig. 5 shows how the contribution of the 2.4- and 4.8-Å-decay-length forces to the free energy per DNA phosphate at 25 Å separation depends on the inverse charge of the counterion, 1/N, for both the arginine and amine series, as well as protamine. The 2.4-Å-decay-length repulsive forces for the amine series show a larger variation with N than do those for the arginine series. For protamine, the repulsion is significantly larger than for the arginine series. However, the change in the 2.4-Å-decay-length repulsive free energies for all measured cations is still small compared with the change in energies from the 4.8-Å-decay-length force. The dependence of the attractive free energy on 1/N is strikingly linear for the arginine series from Arg₂ through poly(Arg). Even the attraction for protamine with 21 arginine charges can be well described by the arginine series.

Figure 5.

The contributions from the forces with 2.4-Å (open symbols) and 4.8-Å decay length (solid symbols) to the free energy of DNA interaction at 25 Å are shown as a function of the inverse charge N, for polyamines (circles), arginines (squares), and protamine (triangles). The solid line is a linear fit to Arg₂–poly(Arg). Changes in the repulsive amplitude at forces of 2.4 Å decay length are small relative to those at forces of 4.8 Å decay length . Salmon protamine chloride, despite having a complex chemistry consisting of ∼2/3 arginine residues in a 32-amino-acid protein, shows a higher amplitude of force at 2.4 Å decay length than does the pure arginine series, but the attraction is well described by the arginine series line.

Discussion

We previously postulated that the forces between DNA helices in arrays spontaneously condensed by multivalent ions could be accounted for by hydration or water-structuring interactions. Fits to condensed cobalt-hexammine (Co(NH₃)₆³⁺)-DNA force data were shown to be consistent with an attractive exponential force of ∼4.6 Å decay length balanced at the equilibrium spacing by a repulsive exponential force with half the decay length, 2.3 Å (19). More recently, by combining the osmotic-stress pushing experiments with single-molecule magnetic-tweezers pulling experiments, we were able to separate the attractive and repulsive free energies at the equilibrium spacing for some commonly used condensing agents (19). The ratio between attractive and repulsive free energies at the equilibrium spacing is consistent with the ratio of decay lengths for the attractive and repulsive exponential forces, a factor of ∼2, consistent with the previous predictions. In these latter measurements, the two best-fitting exponential decay lengths were 2.4 and 4.8 Å.

The experimental results can also be rationalized by electrostatic interactions. Within the formulism of Kornyshev and Leikin (31,33,34), the attractive force of longer decay length is an electrostatic interaction with a decay length dominated by the helical pitch of DNA. The repulsive force that dominates at close distances is an image charge repulsion due to the significant dielectric constant discrepancy between water and the DNA core. The ratio of the exponential force decay lengths is necessarily a factor of 2.

Within the hydration force formulism, the exponential repulsive force of shorter decay length is the hydration equivalent of the image charge repulsive force in electrostatics. The hydration atmosphere extending from a solvated surface stabilizes water structuring at the surface. Disruption of the atmosphere by replacing water with another surface will lower hydration energies regardless of the water structuring on the other surface. Repulsion should depend predominantly on the water structuring of groups on the DNA surface and, as with electrostatic image charge repulsion, on the mode of binding (phosphate backbone or grooves), but not on the correlations of these groups on apposing helices. Just as electrostatic attraction results from the direct interaction of surface charges, hydration attraction results from the direct interaction of surface hydration structures. Perturbations in water structure around one surface due to the close presence of another surface can either weaken or strengthen hydration energies, depending on the mutual structuring of water. We postulated that the attractive force had the same exponential decay length as observed previously for repulsive hydration forces, but that the force was now attractive because of correlations in complementary water structuring on apposing helices.

Despite its simplicity, the double-exponential form of Eqs. 2 and 3 with 2.4- and 4.8-Å decay lengths gives good fits to all the force data, attractive and repulsive, shown in Figs. 2 and 4: for the arginine series from Arg₁ at high concentrations to +6 Arg₆ and poly(Arg), for the amine series starting with univalent DMA⁺¹ at high concentrations through +4 spermine, and for the 32-amino-acid peptide +21 salmon protamine, as well as for the comparatively small trivalent metal complex Co(NH₃)₆³⁺ previously reported (17–19). This commonality strongly indicates that these two forces dominate DNA-DNA interactions at close distances regardless of the nature of the condensing ion.

The depths of the free-energy minimum per DNA phosphate at the equilibrium spacing calculated from the double-exponential fits (Fig. 3) are quite small. This agrees with our previous estimates (17) and recent optical-tweezers measurements (19). It is worth noting that the measured free-energy minima for DNA condensed by Co(NH₃)₆³⁺, a compact trivalent metal ion, and by Arg₃³⁺ or spermidine³⁺, a linear array of three univalent charges spread over ∼11 Å, are almost equal, even though helices are significantly closer in the Co(NH₃)₆³⁺-condensed DNA. The similar small free-energy minima suggest that it is only necessary that the charges of the counterion be linked, not that the charge density be high.

The exponential force of 2.4 Å decay length is likely image-charge repulsion or its hydration equivalent. In either case, the decay length is expected to be half of that for direct electrostatic or hydration interaction between surfaces. There is some variation in force amplitude seen with the arginine series between Arg₁ and Arg₆ (∼40%). Around half of the variation occurs between Arg₁ and Arg₂. The changes could be due to differences in DNA binding, i.e., bound on the DNA surface or in the diffuse atmosphere, where it is shared more equally by apposing helices, or to differences in the DNA-surface binding mode, i.e., delocalized, in grooves, or to the sugar-phosphate backbone. The presence of a strong 1,1,0 reflection in the x-ray scattering from poly(Arg)-DNA fibers has been taken as evidence that poly(Arg) binds in at least one of the DNA grooves (39). Incorporating Raman spectroscopy data, Hud et al. constructed a model in which arginine-rich protamine binds compactly in the major groove, completely neutralizing the DNA phosphates (40). We also see the 1,1,0 reflection for Arg₂ (after the transition to attraction) through Arg₆ and protamine, but not for Arg₁, the complete polyamine series, or, for example, Na⁺, Mg²⁺, or Co(NH₃)₆³⁺. Even if the latter are bound in the grooves, however, there might not be enough electron density compared with arginine to give a strong 1,1,0 reflection.

The slight variation in the 2.4-Å-decay-length exponential force amplitude seen in the Arg₂–Arg₆ series may also be due to slight differences in repulsive amplitude between the terminal CO₂⁻ and –NH₃⁺ groups and the peptide bond, -CO-NH-. The relative contributions of these moieties vary with the length of the arginine peptide. The comparatively large increase in repulsive force amplitude for poly(Arg) could reflect a lack of order in binding such a long peptide to DNA. The evidence provided in this article indicates that the larger repulsive amplitude seen for protamine is due at least in part to the presence of uncharged amino acids (J. DeRouchey and D. Rau, unpublished). There is significantly more variation in the repulsive 2.4-Å-decay-length exponential force amplitude for the polyamine series (Fig. 5), likely due to differences in either binding or force amplitude between secondary and tertiary amines. Significant variation in binding location has been reported for polyamines (41–45).

Of more importance is that the change in amplitude of the 2.4-Å-decay-length exponential force observed for the arginine or polyamine series is small compared with changes in 4.8-Å-decay-length exponential force (Fig. 5). The decrease in equilibrium spacing between helices, with increasing peptide length from Arg₂ through Arg₆, is almost entirely due to an increase in the attractive amplitude of the 4.8-Å-decay-length exponential force.

The striking feature of the 4.8-Å-decay-length exponential force (Fig. 5) is the nearly linear dependence of its amplitude on the inverse charge of its arginine peptide. Even the attraction for the 32-amino-acid peptide protamine, with 21 arginines, is well described by the best-fit line for the Arg₂–polyarginine series. The approximate linear dependence does not describe well the Arg₁ repulsion force with 4.8 Å decay length. This may be related to a potentially greater variability in binding properties for monovalents. The attractive force amplitudes for +3 spermidine and +4 spermine are very close to those for +3 Arg₃ and +4 Arg₄, respectively. This implies that charge alone determines the amplitude of the force with 4.8 Å decay length. However, without knowing the number and location of counterion charges on DNA, it is difficult to conclude unambiguously that charge is the only important property.

Attraction between DNA helices is certainly the result of the favorable positioning of phosphate and counterion charges on apposing helices. It is difficult, though, to parse the energy contributions from direct coulombic interaction and from indirect water restructuring. We have hypothesized that water structuring forces dominate the close interactions between DNA helices rather than traditional electrostatics because of the similarity of forces among several different systems. The forces between charged helices such as DNA or xanthan in the last 10–15 Å of surface separation resemble the forces between zwitterionic lipid bilayers and completely uncharged macromolecules like schizophyllan and hydroxypropyl cellulose (46–49). The exclusion of salts such as NaF and NaCl, zwitterionic solutes such as betaine glycine, and uncharged polar solutes such as sorbitol from hydroxypropyl cellulose, as well as the exclusion of nonpolar solutes from DNA, all show a similar exponential dependence on distance for forces of 2- to 4-Å decay length (50–52).

The electrostatic zipper model developed by Kornyshev and Leikin (31,33,34) for DNA condensation is a convenient model for considering interhelical charge correlations. The basic formalism, developed specifically for electrostatic forces, applies also to hydration interactions. Counterions that bind in DNA grooves can result in attraction (after optimizing the mutual azimuthal alignment of apposing helices) that has been termed an electrostatic zipper motif. Briefly, the overall magnitude of the attractive force depends on the fraction of DNA charge neutralized and the fraction of neutralizing charge found in the major or minor grooves. There is still a repulsive, non-image-charge force that depends on the fraction of charge neutralized. A very simple explanation for the ∼1/N dependence is that the residual charge on the DNA helix after counterion binding decreases as 1/N within Manning theory and that attraction then correspondingly increases with the fraction of DNA charge neutralized and bound in a groove. If the counterion binds only in the major groove, then the dependence of the attractive energy term from Kornyshev and Leikin (the function u₁(R) of Eq. 57 in Kornyshev et al. (31)) on the charge of the bound counterion N within Manning theory is ∼(1.3 − .24/N)². The 1/N term dominates the (1/N)² term and the dependence will appear approximately linear with 1/N. It is not clear, however, that Manning theory can be reliably applied to dense arrays of DNA.

There is also the possibility that the mode of counterion binding can change to optimize attraction, as illustrated in Fig. 1. There could be a shift in ion binding from the diffuse ion atmosphere or from delocalized and phosphate bound counterions to the grooves for better interhelical correlation. The attractive energy gained with correlation of a single counterion will increase with the number of interacting charges N. To a first-order approximation, the entropy loss associated with the restriction of binding sites will be about the same for each bound counterion, with little or no N dependence. There is less loss of entropy to correlate one +4 counterion than four +1 ions.

Conclusions

The osmotic stress force curves for DNA helices in the presence of homologous series of arginine and polyamine cations, as well as for a naturally occurring protein, salmon protamine, are all curves well described by a double-exponential fit with 2.4- and 4.8-Å decay lengths. Separation of the attractive and repulsive components of the free energy of interaction in DNA condensation tells us much about the cation-dependent thermodynamic forces. For a given homologous cation species, the repulsive amplitudes of the force with 2.4 Å decay length vary only slightly with length compared with changes in the exponential force with 4.8 Å decay length. The long-range force amplitude varies monotonically, with cation length, or charge, ranging from repulsive for monovalents to attractive for polyvalent cations driving DNA to condense spontaneously into hexagonal arrays. The calculated attractive free energies for arginines, polyamines, and protamine are all found to collapse to a single curve that varies inversely with cation repeat number N. The force characteristics and dependences on cation charge can be rationalized by both hydration and electrostatic theories.