Linear Mixed Models for Skew-Normal Independent bivariate responses with an application to Periodontal Disease

Abstract

Bivariate clustered (correlated) data often encountered in epidemiological and clinical research are routinely analyzed under a linear mixed model framework with underlying normality assumptions of the random effects and within-subject errors. However, such normality assumptions might be questionable if the data-set particularly exhibit skewness and heavy tails. Using a Bayesian paradigm, we use the skew-normal/independent (SNI) distribution as a tool for modeling clustered data with bivariate non-normal responses in a linear mixed model framework. The SNI distribution is an attractive class of asymmetric thick-tailed parametric structure which includes the skew-normal distribution as a special case. We assume that the random effects follows multivariate skew-normal/independent distributions and the random errors follow symmetric normal/independent distributions which provides substantial robustness over the symmetric normal process in a linear mixed model framework. Specific distributions obtained as special cases, viz. the skew-t, the skew-slash and the skew-contaminated normal distributions are compared, along with the default skew-normal density. The methodology is illustrated through an application to a real data which records the periodontal health status of an interesting population using periodontal pocket depth (PPD) and clinical attachment level (CAL).

1. Introduction

Periodontal disease usually refers to a collection of inflammatory disease affecting tissues called periodontium that surround and support the tooth and maintains them in the maxillary (upper jaw) and mandibular (lower jaw) bones. If left untreated, it can cause progressive bone loss around the tooth with loosening and eventual loss. It is well documented that some 5% to 15% of any population is susceptible to severe generalized periodontitis worldwide [1]. Being the primary cause of adult tooth loss, it has been estimated that about 50% of U.S. adults over the age of 35 experience early stages of periodontal disease [2]. Periodontal progression is usually assessed by hygienists by measuring two correlated popular bio-markers, viz. periodontal pocket depth (PPD) and clinical attachment level (CAL) [3].

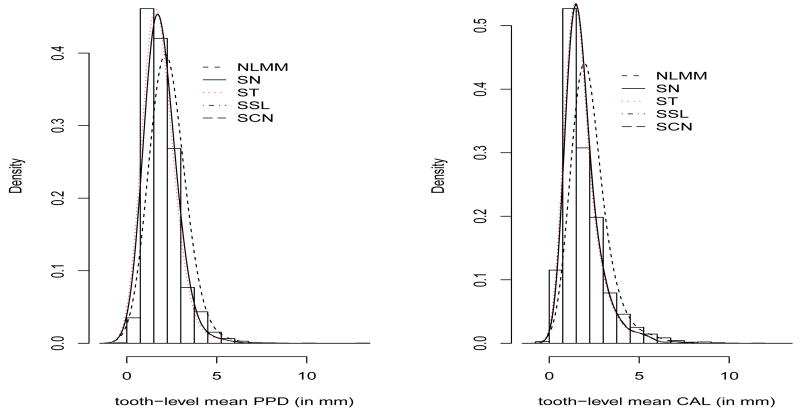
The motivating data example for this paper comes from a clinical study conducted at the Medical University of South Carolina (MUSC) to determine the periodontal disease status of Type-2 diabetic Gullah-speaking African-Americans. For an overall tooth level periodontal status, our bivariate response is the mean of the measurements, i.e. mean PPD and mean CAL for the 6 sites observed simultaneously for each tooth nested within a subject. More details on this data appears in Section 2. With this type of multiple outcome measures, the underlying statistical question is to estimate the functions that model their dependence on co-variates as well as to investigate the relationship between these functions. Similar clinical and epidemiological studies often generate clustered as well as longitudinal follow-up data with bivariate or multivariate outcomes as primary endpoints which are routinely analyzed using multivariate linear mixed models [4]. In this paper, we focus on a linear mixed effects model that accommodates the tooth level clustering within subjects as well as the correlation among bivariate (PPD and CAL) measures and facilitates borrowing of strength across all teeth when assessing the effects of co-variates, viz. age, gender, body mass index (obesity status), glycemic control (diabetic status), etc. on periodontal disease progression. We seek to address the pertinent question: ‘How do potential co-variates influence periodontal status of a particular tooth after accounting for subject-level clustering?’. In traditional linear mixed model (LMM) analysis [5], the correlation due to clustered/repeated measures on a subject are usually accounted for through the inclusion of random effects and within subject measurement-errors which are often assumed to be normally distributed. While such an assumption makes data analysis amenable to popular software like SAS, the usual fidelity to normality assumptions has been questionable [6, 7, 8] when data exhibits non-normal behavior. Figure 1 shows the raw density histogram plots of tooth-level mean PPD (0-14mm) and mean CAL (0-12mm) in our data. The density histograms demonstrate considerable skewness along with (possible) thick tails. A common approach adopted for data analysis in these situations is reverting back to usual multivariate normality assumptions after suitable transformation of the response (viz. log transform) on a continuous scale. Although they may lead to reasonable empirical results, they may be avoided when a suitable alternative theoretical model is available because data transformation hinders underlying data generation mechanisms due to reduced information and often component-wise transformation does not lead to joint normality [9]. Besides, transformations are not universal, i.e. transforms used for one particular data may not be adapted for a different data. Moreover, mean PPD and mean CAL can have zero values and this hinders the applicability of popular log transformations. This motivates researchers to consider exploration of a more general mixed effects framework that takes into account the flexibility in distributional assumptions of random effects and measurement error to produce robust parameter estimates. The term ‘robustness’ is quite extensive; here robustness is achieved with respect to parameter estimation.

Figure 1.

Histograms of tooth-level observed mean PPD and mean CAL scores overlayed with posterior predictive density estimates using normal linear mixed model (NLMM) and skew-normal (SN), skew-t (ST), skew-slash (SSL) and skew contaminated normal (SCN) densities as members of the SNILMM

Considerable research has been done by introducing more flexible parametric families that can accommodate normality departures (skewness and heavy tails) and hence eliminate the need of ad-hoc data transformations [10]. In the context of LMM, the random effects distribution was relaxed using finite normal mixtures [6], smoothing [7], a semi-nonparametric (SNP) density [11] or a thick-tailed normal/independent (NI) densities [12]. Much of recent frequentist and Bayesian advances in regression problems revolve around the attractive and popular skew-normal (elliptical) distributions [10, 13, 14, 15]. Related literature in this context is very rich [8, 16, 17, 18] and the curious reader might choose to venture an entire monograph [19] dedicated to discuss recent developments. Starting with the multivariate skew-normal (SN) density [15], SN linear mixed models (SNLMM) were proposed in [9, 20]. A common feature of these classes of SNLMM's is that the normal linear mixed model (NLMM) is a special member in each class.

In this article, we propose a parametric modeling of LMM for robust estimation using skew-normal/independent (SNI) distributions under a Bayesian paradigm. We assume a SNI distribution for the random effects and a symmetric normal/independent (NI) distribution [28] for the within-subject errors, so that the skew-normal/independent linear mixed model (SNILMM) is defined. The multivariate SNI distributions used in this paper is developed primarily from the multivariate SN density proposed in [14] for Bayesian regression problems and is different from the multivariate SNI densities developed in [21] motivated from the SN version proposed in [15]. However, the differences are only due to the various parameterizations [22] used and an unification of all skew-normal (elliptical) variants is presented in [23]. Recent Bayesian implementation of multivariate SN distributions [9] involves skew-normal (SN) and skew-t (ST) densities using a conditional stochastic representation. Starting from a marginal stochastic representation as in [8, 20], our SNI distributions are amenable to Bayesian implementation and provides a unified class of skew-thick-tailed densities particularly attractive for robust parametric inference and contains as proper elements not only the SN, ST but also the skew-slash (SSL) and the skew-contaminated normal (SCN) densities.

The rest of the paper unfolds as follows. Section 2 illustrates the motivating data behind this research. In Section 3, we introduce the SNI distributions for our bivariate response setup and propose Bayesian inference and related model comparison techniques. We apply our SNILMM to the periodontal data in Section 4 and use model selection tools to determine the best model, comparing between the elements of the SNI class as well as the traditional NLMM. Conclusions and future developments are relegated to Section 5.

2. Periodontal disease data

The motivating data analyzed in this paper was collected from a clinical study [24] conducted at the Medical University of South Carolina (MUSC). The study was primarily aimed to explore the relationship between periodontal disease and diabetes level (determined by Hba1c, or ‘glycosylated hemoglobin’) in Type-2 diabetic Gullah-speaking (or simply Gullah) African-Americans (13 years or older) residing in the coastal sea-islands of South Carolina. The substantial evidence of adverse effects of diabetes on periodontal health [25] has been extensively explored in dental research. The 2006 American Diabetes Association (ADA) Standards of Medical Care recommend diabetic patients strive to maintain the HbA1c < 7, ideally between 4-6 [26]. Since this is part of an ongoing study, we selected 214 patients with complete covariate information.

To measure periodontal status/progression, dental hygienists usually record the periodontal pocket depth (PPD) and clinical attachment level (CAL), both measured in mm using a manual probe for 6 surfaces per tooth (disto-buccal, mid-buccal, mesio-buccal, disto-lingual, mid-lingual and mesio-lingual) for all 28 teeth per subject, except the third molars. Figure 2(a) provides a pictoral description of the two measures for a single tooth. PPD is defined as the distance (in mm) from the gingival margin to the base of the sulcus/pocket as measured by a periodontal probe. CEJ-GM, or gingival recession is the distance between the free gingival margin and the cemento-enamel junction [3]. The primary measure of perio progression, CAL is defined as CAL = PPD − (CEJ-GM) [3]. Clearly, site-level PPD and CAL are correlated. In our data, we take the mean PPD and mean CAL measures as representative tooth-level periodontal status clustered within a subject. Note that CEJ-GM was recorded as negative when the free gingival margin recessed below the cemento-enamel junction (CEJ). From the raw plot of mean PPD and mean CAL in Figure 2(b), we suspect some positive correlation between the two response measures. Additionally several subject level covariates were also collected in the study, viz. Age (in years), Gender (1=Female, 0=Male), Body Mass Index or BMI (in kg/m²), glycemic status or Hba1c (1= High, 0 = controlled), etc. The mean age of the subjects is about 55 years with a range from 26-87 years. Female subjects seem to be predominant (about 75%) in our data, which is not uncommon in this population[27]. About 70% of subjects are obese (BMI >= 30) and 65% are with Hba1c >= 7, an indicator of high glycemic level.

Figure 2.

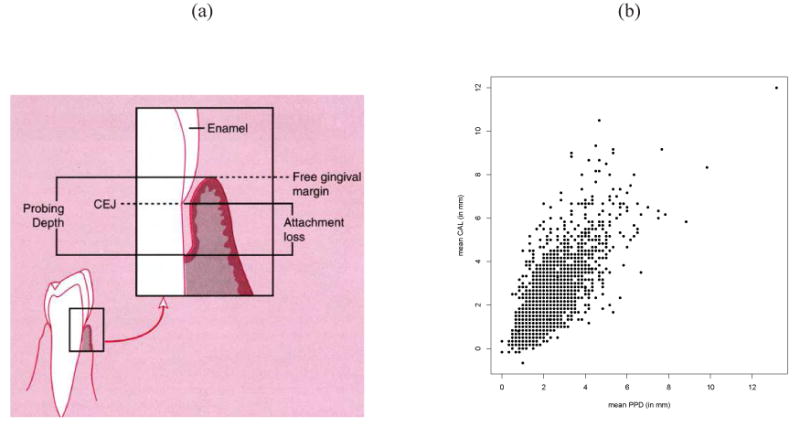
Panel (a): Graphical illustration of PPD and CAL measures for a tooth. This figure was published in ‘Dental Hygiene: Theory and Practice’, 1st edition, Michele L. Darby and Margaret M. Walsh, Chapter 17 Page 471, Copyright W.B.Saunders Company (1995); Panel (b): Scatter plot of mean PPD vs mean CAL values

3. Statistical Model and Bayesian Inference

3.1. Skew-normal independent distributions

We start with the definition of the SN distribution proposed in [14] as an alternative to [15] for straightforward Bayesian inference. A p × 1 random vector Y follows a SN distribution with p × 1 location vector μ, p × p positive definite dispersion matrix Σ and p × p asymmetry matrix Λ = Diag(λ) where Diag(·) is a diagonal matrix, λ = (λ₁,…, λ_p)^⊤, written as Y ∼ SN_p,p(μ, Σ, Λ), if its pdf is given by

$$f(\mathbf{\text{y}})=2^p{\mathit{\phi }}_p(\mathbf{\text{y}};\mathit{\text{μ}},\mathbf{\Omega }){\Phi }_p({\mathbf{\Lambda }}^{\top }{\mathbf{\Omega }}^{-1}(\mathbf{\text{y}}-\mathit{\text{μ}});\mathbf{\Delta }),$$ (1)

where Ω = Σ + ΛΛ^⊤, Δ = (I_p + Λ^⊤ Σ⁻¹ Λ)⁻¹ = I_p − Λ^⊤ Ω⁻¹ Λ, I_p is the p × p identity matrix, ϕ_p(.; μ, Σ) and Φ_p(.; Σ) are, respectively, the probability density function (pdf) of N_p(μ, Σ) and cumulative distribution function (cdf) of N_p(0, Σ). Following [22], we use the notation SN_p,p since both the symmetric kernel ϕ_p and the skewing function Φ_p are p-variates. Note that for Λ = 0_p×p (or λ = 0_p×1) where 0_p×p and 0_p×1 are respectively a p × p matrix and a p × 1 vector of zeroes, (1) reduces to the symmetric N_p(μ, Σ)-pdf, while for non zero values of Λ, it produces a perturbed (asymmetric) family of N_p(μ, Σ)-pdf's.

Following [21], we define a SNI distribution as a process of the p-dimensional random vector

$$\mathbf{\text{y}}=\mathit{\text{μ}}+U^{-1/2}\mathbf{\text{Z}},$$ (2)

where U is a positive random variable with cdf H(u∣ν) and pdf h(u∣ν), which is independent of the SN_p,p(0, Σ, Λ) random vector Z. Here the parameter ν is a scalar or vector indexing the distribution of U. Given U = u, Y follows a multivariate skew–normal distribution with location vector μ, scale matrix u⁻¹Σ and asymmetry matrix u^−1/2Λ, i.e., Y∣U = u ∼ SN_p,p(μ, u⁻¹Σ, u^−1/2Λ). Thus, U is affecting both Σ and Λ. From (1), the marginal pdf of Y is:

$$f(\mathbf{\text{y}})=2^p{\mathit{\int }}_0^{\infty }{\phi }_p(\mathbf{\text{y}};\mathit{\text{μ}},u^{-1}\mathbf{\Omega }){\Phi }_p(u^{1/2}{\mathbf{\Lambda }}^{\top }{\mathbf{\Omega }}^{-1}(\mathbf{\text{y}}-\mathit{\text{μ}});\mathbf{\Delta })dH(u\mid \nu )\mathbf{.}$$ (3)

The notation Y ∼ SNI_p,p(μ, Σ, Λ, H) will be used when Y has pdf (3). When Λ = 0, the SNI distributions reduces to the respective normal-independent (NI) [28], represented by the pdf $f_0(\mathbf{\text{y}})={\mathit{\int }}_0^{\infty }{\phi }_p(\mathbf{\text{y}};\mathit{\mu },u^{-1}\sum )dH(u;\mathit{\nu })$. We will use the notation Y ∼ NI_p(μ, Σ, H) when Y has distribution in the NI class. The asymmetrical class of SNI distributions includes the skew-t, the skew-slash and the skew contaminated normal distributions, all of which accommodates heavy tails than the SN and can be used for robust inference. Further technical details on skew-normal and skew-normal/independent distributions can be downloaded from the Supplementary Material available at http://people.musc.edu/∼bandyopd/SupplementSNIDental.pdf

3.2. Skew-normal/independent linear mixed models

Now, we summarize the linear mixed model (LMM) for our periodontal progression data with bivariate correlated responses. Let ${\mathbf{\text{Y}}}_i^P={(Y_{i1}^P,Y_{i2}^P,\dots ,Y_{i{m}^P}^P)}^T$ and ${\mathbf{\text{Y}}}_i^C={(Y_{i1}^C,Y_{i2}^C,\dots ,Y_{i{m}^C}^C)}^T$ be the measurements (in mm) of tooth-level mean PPD and CAL, respectively, for subject i (i = 1, …, n). Here, m^P and m^C denotes the number of teeth accounted for within a particular mouth, without loss of generality which is 28 (excluding the third molars). Any missing tooth measurements were not included in the study. Let ${\mathbf{\text{X}}}_i^P$ and ${\mathbf{\text{X}}}_i^C$ be the m^P × p₁ and m^C × p₂ design matrix associated with the fixed effects β^P and β^C of the two markers respectively and ${\mathbf{\text{Z}}}_i^P$ and ${\mathbf{\text{Z}}}_i^C$ be the corresponding m^P × q₁ and m^C × q₂ design matrices associated with the random effects ${\mathbf{\text{b}}}_i^P$ and ${\mathbf{\text{b}}}_i^C$ respectively. Thus, we have our bivariate LMM:

$${\mathbf{\text{Y}}}_i=\left[\begin{array}{c}{\mathbf{\text{Y}}}_i^P\\ {\mathbf{\text{Y}}}_i^C\end{array}\right]=\left[\begin{array}{cc}{\mathbf{\text{X}}}_i^P& \mathbf{0}\\ \mathbf{0}& {\mathbf{\text{X}}}_i^C\end{array}\right]\left[\begin{array}{c}{\mathit{\beta }}^P\\ {\mathit{\beta }}^C\end{array}\right]+\left[\begin{array}{cc}{\mathbf{\text{Z}}}_i^P& \mathbf{0}\\ \mathbf{0}& {\mathbf{\text{Z}}}_i^C\end{array}\right]\left[\begin{array}{c}{\mathbf{\text{b}}}_i^P\\ {\mathbf{\text{b}}}_i^C\end{array}\right]+\left[\begin{array}{c}{\mathbf{\text{e}}}_i^P\\ {\mathbf{\text{e}}}_i^C\end{array}\right],$$ (4)

where ${\mathbf{\text{e}}}_i^P$ and ${\mathbf{\text{e}}}_i^C$ are the within-subject residuals for the mean PPD and mean CAL, respectively. For robust estimation, we model b_i and e_i simultaneously as

$${({\mathbf{\text{b}}}_i^{\top },{\mathbf{\text{e}}}_i^{\top })}^{\top }\stackrel{\mathit{\text{ind}}.}{\sim }{\text{SNI}}_{n_i+q,n_i+q}({\mathbf{0}}_{n_i+q},{\sum }_{b{e}_i},{\mathbf{\Lambda }}_{b{e}_i},H),i=1,\dots ,n,$$ (5)

where Σ_bei = Diag(D, Σ_i) and ${\mathbf{\sum }}_i=\text{Diag}({\sigma }_1^2{\mathbf{\text{I}}}_{m^P},{\sigma }_2^2{\mathbf{\text{I}}}_{m^C})$ with Diag(A, B) denoting a block diagonal matrix whose elements are the square matrices A and B; q = q₁ + q₂, $n_i=m_{\mathit{\text{i}}}^P+m_{\mathit{\text{i}}}^C$, the matrix D = D(α) is the dispersion matrix corresponding to within-subject variability and depending on the unknown parameter α, Λ_bei = diag(Λ, 0_ni×ni), with Λ = Diag(λ) and λ = (λ₁, …, λ_q)^⊤. Thus the vector λ is the only parameter involved in the asymmetry matrix. Finally, H = H(·∣ν) is the cdf-generator that determines the specific SNI model that we are assuming. Integrating out the variable u_i, it follows from (2) and the stochastic representation S-1 in the Supplementary Material, that

$${\mathbf{\text{b}}}_i=({\mathbf{\text{b}}}_i^P,{\mathbf{\text{b}}}_i^C)\stackrel{i.i.d.}{\sim }{\text{SNI}}_{q,q}(\mathbf{0},\mathbf{\text{D}},\mathbf{\Lambda },H),{\mathbf{\text{e}}}_i=({\mathbf{\text{e}}}_i^P,{\mathbf{\text{e}}}_i^C)\stackrel{\mathit{\text{ind}}.}{\sim }{\text{NI}}_{n_i,n_i}(\mathbf{0},{\mathbf{\sum }}_i,H),i=1,\dots ,n.$$

In this modeling, we consider a bivariate generalization of the classical NLMM where the random errors are assumed to follow a NI distribution (with mean zero) and the random effects are assumed to follow a multivariate SNI distribution. As in [21], since for each i = 1, …, n, b_i and e_i are indexed by the same mixing factor U_i, they are not independent in general. The independence corresponds to the case when U_i = 1 (i = 1, …, n), so that the SNILMM reduces to the SNLMM as defined in [20]. However, from (2) and S-1 in the Supplementary Material, conditional on U_i, b_i and e_i are uncorrelated, since $\mathit{\text{Cov}}({\mathbf{\text{b}}}_i,{\mathbf{\text{e}}}_i)=E\left\{{\mathbf{\text{b}}}_i{\mathbf{\text{e}}}_i\right\}=E\left\{E\right\{{\mathbf{\text{b}}}_i{\mathbf{\text{e}}}_i^{\top }\left|U_i\right\}\}=E\{E\left\{{\mathbf{\text{b}}}_i\right|U_i\left\}E\right\{{\mathbf{\text{e}}}_i\left|U_i\right\}\}=0$.

Our main focus is to provide inference for $\mathit{\theta }={({\mathit{\beta }}^P,{\mathit{\beta }}^C,{\sigma }_1^2,{\sigma }_2^2,{\mathit{\alpha }}^{\top },{\mathit{\lambda }}^{\top },{\mathit{\nu }}^{\top })}^{\top }$. Under the SNILMM proposition defined in (4)–(5), the marginal distribution of Y_i is given by

$$f({\mathbf{\text{y}}}_i\mid \mathit{\theta })=2^q{\mathit{\int }}_0^{\infty }{\phi }_{n_i}({\mathbf{\text{y}}}_i;{\mathbf{\text{X}}}_i\mathit{\text{β}},u_i^{-1}{\mathbf{\Psi }}_i){\Phi }_q\left(u_i^{1/2}{\overline{\mathbf{\Lambda }}}_i^{\top }{\mathbf{\Psi }}_i^{-1}({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta });{\mathbf{\Delta }}_{z_i}\right)dH(u_i\mid \mathit{\nu }),$$ (6)

where ${\mathbf{\Psi }}_i={\mathbf{\sum }}_i+{\mathbf{\text{Z}}}_i\mathbf{\Omega }{\mathbf{\text{Z}}}_i^{\top }$, ${\mathbf{\Delta }}_{z_i}={\mathbf{\text{I}}}_q-{\overline{\mathbf{\Lambda }}}_i^{\top }{\mathbf{\Psi }}_i^{-1}{\overline{\mathbf{\Lambda }}}_i$, β = (β^P, β^C)^⊤ and Λ̄_i = Z_iΛ, with Ω = D + ΛΛ^⊤, Λ = Diag(λ₁, …, λ_q), where X_i = diag(X_1i, X_2i), ${\mathbf{\text{Z}}}_i=\text{diag}({\mathbf{\text{Z}}}_i^P,{\mathbf{\text{Z}}}_i^C)$. The proof follows from Theorem 1 given in [20]. We call attention to the fact that the marginal distributions of the response vectors given in (6) does not belong to the SNI class introduced in (3), since in general n_i ≠ q, i.e. the SNI is not closed under linear transformations. The specific forms of the marginal distributions of Y for the sub-classes of our SNILMM are presented in Appendix A.

3.3. Priors and joint posterior distributions

In this sub-section, we describe our choice of priors and associated posterior distributions of model parameters to implement Bayesian inference for our SNILMM. A key feature of this model is that it can be formulated in a flexible hierarchical representation. From (2) and the marginal stochastic representation of a SN random vector (see S-1 in the Supplementary Material), it follows that the SNILMM defined by (4) and (5) can be written hierarchically as:

$${\mathbf{\text{Y}}}_i\mid {\mathbf{\text{b}}}_i,T_i=t_i,U_i=u_i\stackrel{\text{ind}.}{\sim }{N}_{n_i}({\mathbf{\text{X}}}_i\mathit{\beta }+{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i,u_i^{-1}{\sum }_i),$$ (7)

$${\mathbf{\text{b}}}_i\mid T_i=t_i,U_i=u_i\stackrel{\text{ind}.}{\sim }{N}_q(\mathbf{\Lambda }{\mathbf{\text{t}}}_i,u_i^{-1}\mathbf{\text{D}}),$$ (8)

$${\mathbf{\text{T}}}_i\mid U_i=u_i\stackrel{\text{ind}.}{\sim }T{N}_q(0,u_i^{-1}{\mathbf{\text{I}}}_q;{ℝ}_{+}^p),$$ (9)

$$U_i\stackrel{\text{iid}}{\sim }H(u_i\mid \nu ),$$ (10)

i = 1, …, n, where X_i = Diag(X_1i, X_2i), β = (β_P, β_C)^⊤, ${\mathbf{\text{Z}}}_i=\text{Diag}({\mathbf{\text{Z}}}_i^P,{\mathbf{\text{Z}}}_i^C)$, ${ℝ}_{+}^p$ denotes the Euclidean vector space of all p-tuples of positive real numbers and TN_p(μ, Σ; A) denotes a p-variate truncated normal distribution for N_p(μ, Σ) lying within the hyperplane A. Defining $\mathbf{\text{y}}={({\mathbf{\text{y}}}_1^{\top },\dots ,{\mathbf{\text{y}}}_{\mathit{\text{n}}}^{\top })}^{\top }$, $\mathbf{\text{b}}={({\mathbf{\text{b}}}_1^{\top },\dots ,{\mathbf{\text{b}}}_{\mathit{\text{n}}}^{\top })}^{\top }$, t = (t₁, …, t_n)^⊤, u = (u₁, …, u_n)^⊤ and _{A}(.) to be the indicator function of the set A, it follows that the complete likelihood function associated with (y^⊤, b^⊤, t^⊤, u^⊤,)^⊤ is given by

$$L(\mathit{\theta }\mid \mathbf{\text{y}},\mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}})\propto \prod _{i=1}^n[{\phi }_{n_i}({\mathbf{\text{y}}}_i;{\mathbf{\text{X}}}_i\mathit{\beta }+{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i,u_i^{-1}{\sum }_i){\phi }_q({\mathbf{\text{b}}}_i;\mathbf{\Lambda }{\mathbf{\text{t}}}_i,u_i^{-1}\mathbf{\text{D}})\times {\phi }_q({\mathbf{\text{t}}}_i;0,u_i^{-1}{\mathbf{\text{I}}}_q){\mathbb{\text{I}}}_{\left\{{ℝ}_p^{+}\right\}}({\mathbf{\text{t}}}_i)h(u_i\mid \nu )].$$ (11)

Now, to complete the Bayesian specification of the model, we need to put prior distribution on all the unknown parameters in θ. Since we have no prior information from historical data or from previous experiments, we assign conjugate but weakly informative priors to obtain well defined and proper posteriors. A popular choice to ensure posterior propriety in a LMM is to consider proper (but diffuse) conditionally conjugate priors like non-informative Normal priors (with large variance) for the fixed-effects, inverse gamma priors for a single variance components and inverse Wishart priors for the variance-covariance matrix, as suggested in [32, 33]. In general, we choose:

$$\begin{array}{l}\mathit{\beta }\sim N({\mathit{\beta }}_0,{\mathbf{\text{S}}}_{\mathit{\beta }}),\\ {\sigma }_k^2\sim IG({\tau }_k/2,T_k/2),k=1,2,\\ \mathbf{\text{D}}\sim I{W}_q({\mathbf{\text{T}}}_{\mathbf{\text{b}}},{\tau }_b),\\ \mathit{\lambda }\sim N_q({\mathit{\lambda }}_0,{\mathbf{\text{S}}}_{\lambda }),\end{array}$$

where N(., .) is the multivariate normal density, IG(a, b) is the inverse gamma density with parameters a and b and IW_q(T_b, τ_b) is the q-variate inverse Wishart distribution where T_b is a q × q positive definite scale matrix and hyperparameter τ_b is the degrees of freedom. The prior distribution of ν, with density π(ν), depends on the particular SNI distribution we use. For the specific SNI distributions discussed in this work, i.e. skew-t (ST), skew-slash (SSL) and skew contaminated normal (SCN) models, our choice is

1. For the skew-t model: $\nu \sim \text{Exp}(\frac{\rho }{2}){\mathbb{\text{I}}}_{\{(2,\infty )\}}$. That is, the degrees of freedom parameter ν has a truncated exponential prior distribution on the interval (2, ∞), with mean 2/ϱ before truncation. The truncation point was chosen to assure finite variance.

2. For the skew-slash model: A Gamma(a, b) distribution with small positive values of a and b(b ≪ a) is adopted as a prior distribution for ν.

3. For the skew-contaminated normal model: A U(0, 1) distribution is used as a prior for ν₁, and an independent Beta(a, b) is adopted as prior for ν₂ to achieve conjugacy.

Assuming elements of the parameter vector to be independent, the joint prior distribution of all unknown parameters is given by

$$\pi (\mathit{\theta })=\pi (\mathit{\beta })\left(\prod _{k=1}^2\pi ({\sigma }_k^2)\right)\pi (\mathit{\lambda })\pi (\mathbf{\text{D}})\pi (\nu ).$$ (12)

Combining the likelihood function (11) and the prior distributions, the joint posterior distribution for θ is now,

$$\pi (\mathit{\beta },{\sigma }_1^2,{\sigma }_2^2,\mathbf{\text{D}},\mathit{\lambda },\mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}}\mid \mathbf{\text{y}})\propto \prod _{i=1}^n[{\phi }_{n_i}({\mathbf{\text{y}}}_i;{\mathbf{\text{X}}}_i\mathit{\beta }+{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i,u_i^{-1}{\sum }_i){\phi }_q({\mathbf{\text{b}}}_i;\mathbf{\Lambda }{\mathbf{\text{t}}}_i,u_i^{-1}\mathbf{\text{D}})\times {\phi }_q({\mathbf{\text{t}}}_i;0,u_i^{-1}{\mathbb{\text{I}}}_q){\mathbb{\text{I}}}_{\left\{{ℝ}_p^{+}\right\}}({\mathbf{\text{t}}}_i)h(u_i\mid \nu )]\pi (\mathit{\theta }).$$ (13)

Distribution (13) is analytically intractable but MCMC methods such as the Gibbs sampler and Metropolis-Hastings algorithm can be used to draw samples, from which features of marginal posterior distribution of interest can be inferred. Given u, all conditional posterior distributions are as in a standard SNLMM and have the same form for any element of the SNI class. An outline of the conditional posteriors of all model parameters including u and ν (for specific SNI distributions) are given in Appendix B.

3.4. Model selection and goodness-of-fit

To select our best fitting model and related goodness of fit assessments, we compare among the SN, ST, SSL and SCN models as well as the NLMM using Bayesian model selection tools. Specifically, we consider both deviance-based criterion [29] and measures based on posterior predictive performance [31].

The DIC [29] is a deviance-based measure appropriate for Bayesian model selection and is defined as DIC = D̄ + p_D, where D̄ is the posterior expectation of the deviance summarizing model-fit, p_D is a measure of model complexity defined as D̄ − D(Θ̄), where D(Θ̄) is the deviance computed at the posterior mean of parameters and Θ denote the parameter space. Analogous to the AIC, the DIC summarizes the relative fit between a model and the ‘true model’ generating the data conditional on the data clusters, i.e, the study subjects using a single number summary with smaller values indicating better fit.

We also consider model selection based on predictive performance of competing models. If y_pr denotes the predictive data vector, then the posterior predictive distribution is given by:

$$p({\mathit{\text{y}}}_{pr}\mid \mathit{\text{y}})=\int p({\mathit{\text{y}}}_{pr}\mid \Theta )p(\Theta \mid \mathit{\text{y}})d\Theta .$$ (14)

One can obtain predictive data easily from a converged posterior sample and samples from the posterior predictive distribution are replicates of the observed model generated data. Using a squared-error loss function [30], we compare competing models based on the expected total predictive deviance (ETPD) defined by

$$\text{ETPD}=E\{\sum _{ij}{(y_{ij,pr}^P-y_{ij}^P)}^2\mid y_{ij}^P\}+E\{\sum _{ij}{(y_{ij,pr}^C-y_{ij}^C)}^2\mid y_{ij}^C\}$$

where, y_ij,Pr denote a replicate of the observed y_ij, the summations are taken over all observations and the expectations taken over the full posterior of all model parameters. Similar to DIC, this criterion chooses the model where the predictive values are centered near observed values, i.e. with the lowest predictive variation.

To determine model adequacy after selecting the best model, we use a discrepancy measure based on (14). If the observed value is extreme relative to the reference distribution (the posterior predictive distribution), there is some concern with respect to assessment of model-fit to the data. Define $y_{ij}^C$ and $y_{i\mathit{\text{j}}}^P$ to be the observed data on tooth-level mean CAL and PPD scores respectively. The discrepancy measure between model and data is computed as a summary statistic [31] using model parameters and data defined as

$$T^k(y,\Theta )=\sum _{i,j}\frac{{(y_{ij}^k-E\{y_{ij}^k\mid \Theta \})}^2}{\mathit{\text{Var}}\left\{y_{ij}^k\mid \Theta \right\}},k=\text{P},\text{C},$$ (15)

The Bayesian p-value/posterior predictive p-value [31] $p_{\mathit{\text{B}}}^k$ is defined as the number of times T^k(y_pr, Θ) exceeds T^k(y, Θ) out of L simulated draws i.e. $p_{\mathit{\text{B}}}^k=\text{Pr}(T^{\mathit{\text{k}}}(y_{p\mathit{\text{r}}},\Theta )\ge T^{\mathit{\text{k}}}(y,\Theta )\mid y)$, where y_pr denotes a simulated draw from (14). A very large p-value (> 0.95) or a very small (< 0.05) both signals model misspecification, i.e. the observed pattern would be unlikely to be seen in replications of the data under the true model [31]

4. Data analysis and findings

In this section, we apply our method to the periodontal data described in Section 2. Our SNI class of distribution allows continuous variation from symmetry to asymmetry and accommodates practical values of kurtosis. We posit 5 competing models with latent (unobserved) random effects and random errors from the SNI class. The models are as follows:

• Model 1 (N): Normal distribution for the latent random effect and random error.

• Model 2 (SN): Skew-normal distribution for the latent random effect and normal distribution for the random error (SN).

• Model 3 (ST): Skew-t distribution for the latent random effect and Student-t distribution for the random error.

• Model 4 (SSL): Skew-slash distribution for the latent random effect and slash distribution for the random error.

• Model 5 (SCN): Skew contaminated normal distribution for the latent random effect and contaminated-normal distribution for the random error.

In the absence of historical data/experiment, we specify practical weakly-informative priors for all model parameters to obtain well-defined (proper) posteriors following the recommendations in [32, 33]. The components of β^P and β^C were assigned independent Normal(0, Precision = 0.01) priors. For the scale parameter ${\sigma }_k^2$, k = 1, 2, we assign a moderately diffuse IG(0.01, 0.01), so that the distribution has mean 1. The prior for the variance-covariance matrix D is taken to be weakly-informative Inverse-Wishart with covariance T_b = Diag((0.01, 0.01)^⊤) and τ_b(degrees of freedom) = 6. For the asymmetry parameters λ₁ and λ₂, independent Normal(0, Precision = 0.01) are used to accommodate either positive or negative skewness and allow the data to determine it, although histogram plots reveal right skewness. Prior choice for ν follows exactly as in [34]. For the ST distribution, we choose ν as Exp(0.1)_{(2,∞)} (i.e. exponential density truncated at 2) to reflect a prior on ν (the t degrees of freedom parameter) with a well defined and finite variance of Y. For the SSL distribution, the prior for ν is a Gamma(a, b) with small positive values of a and b (a = 0.01, b = 0.001), primarily to ensure conjugacy. For the SCN distribution, ν = (ν₁, ν₂)^T and once again for posterior conjugacy, ν₁ is chosen as U(0, 1) and ν₂ as Beta(1, 1)(= U(0, 1)).

For each of the models, we ran 2 chains with widely dispersed initial values. For all the 4 models, viz. N, SN, ST and SSL, we used 80000 iterations with an initial burn-in of 30000. However for the SCN model, convergence was achieved at 60000 iterations. The complexity of the SNI structure is manifested in the relatively high burn-in size. However, this is straightforward to program within WinBUGS and associated code is available from the first author on request. Posterior convergence was assessed using trace plots, autocorrelation plots and the Gelman-Rubin scale-reduction factor R̂ [31]. To reduce autocorrelation among successive Markov draws, we used a spacing of 5. After discarding the initial burn-in samples, we used the remaining samples to compute the posterior parameter estimates.

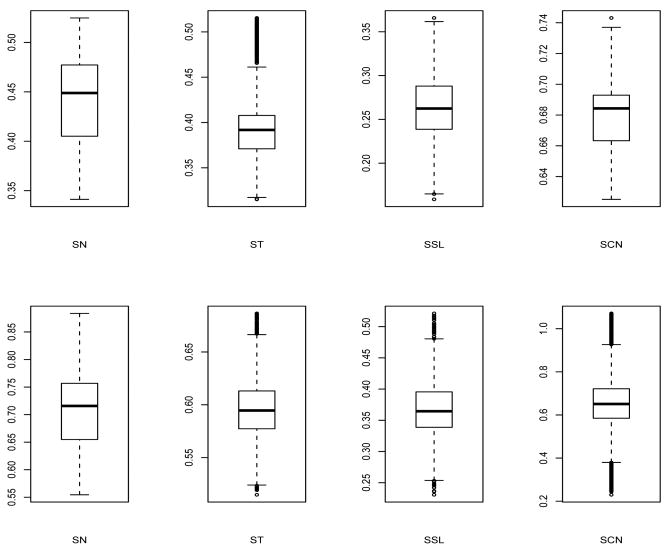
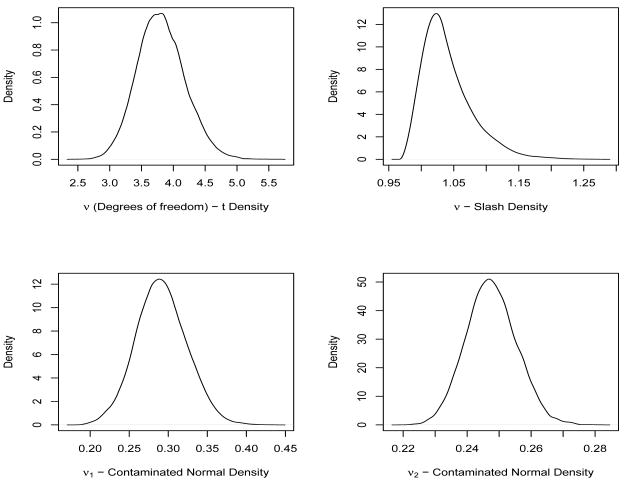
Table 1 presents the comparison among the 5 competing models using Bayesian model choice criterion. Note that all the skewed versions produced better fit (in terms of DIC and ETPD) than the NLMM. In particular, the skew-t (ST) model (with the smallest D̄) produces the best fit among the competing skew models. The SSL model is a close competitor with a lower p_D. Comparing ETPD values, the ST model outperforms all other models, though not substantially. We select Model 3 (ST) as our best fitting LMM. Figure 1 shows the smoothed posterior predictive densities overlayed on raw data histograms for our competing models. From there, it is also quite clear that our class of SNI densities provide a substantial better fit to our data over the NLMM. Also among the 4 competing models, the density for the ST model seems to produce a better fit to the raw data histogram for both the responses. The posterior mean of $p_{\mathit{\text{B}}}^P$ and $p_{\mathit{\text{B}}}^C$ for the ST model are 0.494 and 0.517 respectively, indicating no overall lack of fit using our omnibus statistic (15). Table 2 provides posterior estimates of asymmetry parameters (λ₁, λ₂), the variance components of random errors $({\sigma }_1^2,{\sigma }_2^2)$, the variance-covariance matrix (D) and ν specific to ST, SSL and SCN distributions. In particular, we provide estimates of posterior mean, standard deviation (SD) and 95% credible intervals (CI) for the ST (our best fitting model) and mean and SD for the other models. Interestingly, both λ₁ and λ₂ are significant and positive for all the 4 fitted models providing evidence of moderate right-skewness for our data. Figure 3 shows the box-plots for the parameters λ₁ and λ₂ for all the 4 models. Note that the CI does not include zero for all the models, confirming positive asymmetry of the bivariate responses with mean CAL to be more right-skewed than mean PPD. In particular, estimate (95% CI) of λ₁ and λ₂ for the ST model is 0.3965 (0.3359, 0.4981) and 0.5959 (0.5431, 0.6637) respectively. Figure 4 plots the marginal posterior densities of the parameter ν for ST and SSL densities and ν = (ν₁, ν₂) for the SCN density. All density plots shows some degrees of right asymmetry confirming non-normal nature. For the ST and SSL, as ν (the t degrees of freedom) → ∞ (say 30), it approaches the normal density. However, the posterior mean estimate of ν for ST and SSL model are 3.82 and 1.04 respectively, which confirms its sufficient disparity from the normal framework. Also, the contaminated normal density → normal density when the proportion of contaminants (posterior estimate of ν₁) is 0. For the SCN model, the posterior mean of ν₁ is about 0.34 while the posterior density of ν₂ has a mode around 0.247. The estimate of the within-subject variances ${\mathit{\sigma }}_1^2$ and ${\mathit{\sigma }}_2^2$ for both mean PPD and mean CAL are smaller in the skewed class of models as compared to the NLMM (not shown here), primarily because of interrelation between high variability, heavy tails as well as skewness. Table 3 provides posterior estimates of the fixed-effects parameters obtained by fitting our SNI models. Similar to Table 2, we provide posterior mean, SD and 95% CI's for the ST model and the posterior mean and SD for the other models. For the ST model, the glycemic control (as determined by Hba1c) is positive and significant, indicating that mean PPD and mean CAL values seems to be higher for elevated levels of Hba1c controlling for the other covariates. Although Hba1c is not significant in all other competing models, it was significant in the mean PPD regression for the SL model. Estimates of 95% CI's for almost all fixed effects parameters (for both PPD and CAL regressions) in the ST model were tighter as compared to all other competing models. This is expected, because the ST density seems to provide the most precise fit to this data set. The estimated overall posterior correlation between mean PPD and mean CAL obtained from fitting the ST model is 0.378 which also confirms some degree of positive association between the two measures. For hierarchical GLMMs, use of weakly-informative priors can lead to inference which are sensitive[33, 35] to the choice of priors on hyperparameters. To investigate this issue, we conducted sensitivity analysis on the routine use of inverse-gamma prior [36] on variance components as well as the inverse-Wishart prior of the variance-covariance matrix. In all the results, we focused our attention on the estimation of the fixed effects parameters β^P and β^C. We considered an array of weakly-informative to highly non-informative choice of priors. In particular, we took ${\sigma }_i^2\sim \text{IG}({10}^{{\kappa }_1},{10}^{{\kappa }_1})$, i = 1, 2, where κ₁ ∈ {−4, −3, −2, −1, 0, 1, 2} and the prior choice on the scale matrix D to be Inverse-Wishart with covariance T = Diag((k, k)^⊤), where k = 0.001 and 0.0001. Although we notice slight changes in the values of fixed effects estimates as well as model comparison measures, results were quite robust on the overall and did not change any conclusions regarding our best fitted model, the posterior estimates of λ and ν and the strength of correlation between mean PPD and mean CAL.

Table 1.

Model comparison using DIC and ETPD criteria

Criterion	N	SN	ST	SSL	SCN
D	20815.2	20805.7	17686.0	17732.2	18700.0
pD	384.85	383.56	587.43	563.73	565.24
DIC	21200.05	21189.26	18273.43	18295.93	19265.24
ETPD	2.31	2.24	2.196	2.27	2.251

Table 2.

Posterior parameter estimates of fitting asymmetries and variance components to the periodontal progression data. SD, 2,5% and 97.5% represents standard deviation and percentiles from the posterior distributions of parameters, respectively. s denotes parameter significance.

	SN		ST				SSL		SCN
Parameter	mean	SD	mean	SD	2.5%	97.5%	mean	SD	mean	SD
λ1	0.4862s	0.0575	0.3965s	0.0391	0.3359	0.4981	0.2635s	0.0306	0.3701s	0.0327
λ2	0.7138s	0.0765	0.5959s	0.0286	0.5431	0.6637	0.3619s	0.0373	0.5032s	0.0416
${\sigma }_1^2$	0.4353	0.0095	0.2464	0.0131	0.2221	0.2731	0.1612	0.0098	0.3323	0.0108
${\sigma }_2^2$	0.6889	0.015	0.3546	0.0188	0.3204	0.3938	0.1123	0.0067	0.2286	0.0064
D11	0.4177	0.0522	0.1477	0.023	0.109	0.1971	0.0698	0.0121	0.1549	0.0209
D12	0.5273	0.0642	0.177	0.0263	0.1311	0.2322	0.0797	0.0126	0.1912	0.0246
D22	0.6747	0.0987	0.2238	0.0442	0.1467	0.3193	0.098	0.0185	0.2382	0.0347
ν (ν1 for SCN)			3.82	0.368	3.1171	4.552	1.041	0.0366	0.3388	0.0338
ν2									0.2404	0.0079

Figure 3.

Box plot of asymmetry parameter for the 4 fitted models. The upper row is for λ₁ and the lower row for λ₂.

Figure 4.

Marginal posterior densities estimates of parameter ν for all 4 distributions. The upper panel display plots for skew-t and skew-slash densities and the lower panel for skew contaminated normal density.

Table 3.

Posterior estimates of fixed effects of fitting S-SNI models to the periodontal progression data. SD, 2.5% and 97.5% represents respectively the standard deviation and percentiles from the posterior distributions of parameters. s denotes parameter significance.

	SN		ST				SSL		SCN
Parameter	mean	SD	mean	SD	2.5%	97.5%	mean	SD	mean	SD
IntP	1.665s	0.3639	1.6231s	0.1984	1.175	1.983	1.733s	0.2427	1.744s	0.2691
GenderP	-0.034	0.0978	-0.009	0.0861	-0.175	0.180	-0.0018	0.0791	-0.049	0.0889
AgeP	-0.001	0.0048	-0.004	0.0025	-0.009	0.0001	-0.0048	0.0031	-0.0043	0.0035
BMIP	0.0012	0.0049	-0.001	0.0036	-0.007	0.007	-0.0025	0.0043	-0.0023	0.0048
Hba1cP	0.0730	0.1093	0.1514s	0.0648	0.0169	0.2849	0.1604s	0.0798	0.1594	0.071
IntC	1.025s	0.4657	1.102s	0.2184	0.651	1.48	1.138s	0.2715	1.215s	0.2937
GenderC	-0.0868	0.1359	-0.051	0.0858	-0.237	0.1598	-0.024	0.102	-0.073	0.1129
AgeC	0.0031	0.0062	-0.001	0.003	-0.006	0.004	-0.0018	0.0032	-0.0009	0.0041
BMIC	0.0067	0.007	0.004	0.0042	-0.003	0.013	0.0019	0.0052	0.0019	0.0059
Hba1cC	0.1101	0.1432	0.1594s	0.073	0.0221	0.3096	0.157	0.0891	0.1346	0.0904

5. Conclusions

Using a Bayesian linear mixed model framework, this paper considers a class of multivariate skew-normal/independent (SNI) regression models to jointly analyze mean PPD and mean CAL as determinants of periodontal progression. Our class of SNI models contains as a subclass some interesting family of models, viz. skew-t, skew-slash and skew contaminated normal densities. The nice hierarchical representation given in (7-10) provides easy model implementation using conventional Bayesian software like WinBUGS and thus might appeal to an applied researcher. Using suitable model choice criterion, the skew-t model provided the best fit to this data among other competing models. Since the data exhibit some degree of right-skewness in both components of its bivariate response, substantial improvement in model fit is observed by shifting away from the traditional normality assumptions.

Our approach motivated by a parametric class of skew-densities are relatively easy to implement and provides an interesting alternative to other computationally challenging semiparametric or fully nonparametric models [11, 37]. Although the wonderful memoir [19] provides many alternative expositions of skew-elliptical models, we specifically choose the skew-elliptical distributions starting from the skew-normal representation of [14] due to straightforward Bayesian analysis through hierarchical representations.

Our current analysis is focussed on exploring a ‘clustered’ cross-sectional periodontal progression data. However, often subjects who are brought in for periodontal assessments are subjected to randomized treatments and subsequent longitudinal followups. We plan to explore our class of SNI linear mixed models under these longitudinal framework. Also, periodontal progression is often believed to be associated with latent (within-mouth) spatial structures [38] and a diseased tooth seem to influence its neighboring tooth more than the non-neighbors while accounting periodontal progression. Methods to incorporate spatial dependencies in our class of SNI linear mixed models will be considered elsewhere.

APPENDIX A: Marginal distribution of Y in our LMM for specific SNI cases

For the ST, SL and SCN sub-classes within our SNILMM, we have the following results for the marginal pdf of Y_i as defined in (6).

• The ST distribution

  $$f({\mathit{\text{y}}}_i\mid \mathit{\theta })=2^q{t}_{n_i}({\mathit{\text{y}}}_i;{\mathbf{\text{X}}}_i\mathit{\beta },{\mathbf{\Psi }}_i,\nu )T_q\left(\sqrt{\frac{n_i+\nu }{d_i+\nu }}{\mathbf{\text{A}}}_i;{\mathbf{\Delta }}_{z_i},\nu +n_i\right),$$ (A-1)

  where $d_i={({\mathit{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta })}^{\top }{\mathbf{\Psi }}_i^{-1}({\mathit{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta })$.

• The SSL distribution

  $$f({\mathit{\text{y}}}_i\mid \mathit{\theta })=2^q\nu {\int }_0^1{u}_i^{\nu -1}{\phi }_{n_i}({\mathit{\text{y}}}_i;{\mathit{\text{X}}}_i\mathit{\beta },u_i^{-1}{\mathbf{\Psi }}_i){\Phi }_q\left(u_i^{1/2}{\overline{\mathit{\lambda }}}_i^{\top }{\mathbf{\Psi }}_i^{-1}({\mathit{\text{y}}}_i-{\mathit{\text{X}}}_i\mathit{\beta });{\mathbf{\Delta }}_{z_i}\right)d{u}_i.$$ (A-2)

• The SCN distribution

  $$f({\mathit{\text{y}}}_{\mathbf{\text{i}}}\mid \mathit{\theta })=2^q\left\{{\nu }_1{\phi }_p(\mathit{\text{y}};{\mathit{\text{X}}}_i\mathit{\beta },{\nu }_2^{-1}{\mathbf{\Psi }}_i){\Phi }_q({\nu }_2^{1/2}{\mathbf{\text{A}}}_i;{\mathbf{\Delta }}_{z_i})+(1-{\nu }_1){\phi }_p(\mathit{\text{y}};{\mathit{\text{X}}}_i\mathit{\beta },\mathbf{\Psi }){\Phi }_q({\mathbf{\text{A}}}_i;{\mathbf{\Delta }}_{z_i})\right\}.$$ (A-3)

APPENDIX B: Outline of conditional posterior distributions

Under the full model as described in (13), given u, the full conditional distribution of β, ${\mathit{\sigma }}_1^2$, ${\mathit{\sigma }}_2^2$, D, λ, b_i, t_i, i = 1, …, n, are given as

$$\mathit{\beta }\mid \mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}},{\sigma }_1^2,{\sigma }_2^2,\mathbf{\text{D}},\mathit{\lambda }\sim N_p({\mathbf{\text{A}}}_{\mathit{\beta }}^{-1}{\mathbf{\text{a}}}_{\mathit{\beta }},{\mathbf{\text{A}}}_{\mathit{\beta }}^{-1}),$$ (B-1)

where ${\mathbf{\text{A}}}_{\mathit{\beta }}={\mathbf{\text{S}}}_{\mathit{\beta }}^{-1}+{\sum }_{i=1}^n{u}_i{\mathbf{\text{X}}}_i^{\top }{\sum }_i^{-1}{\mathbf{\text{X}}}_i$ and ${\mathbf{\text{a}}}_{\mathit{\beta }}={\mathbf{\text{S}}}_{\mathit{\beta }}^{-1}{\mathit{\beta }}_0+{\sum }_{i=1}^n{u}_i{\mathbf{\text{X}}}_i^{\top }{\sum }_i^{-1}({\mathit{\text{y}}}_i-{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i)$;

$${\sigma }_k^2\mid \mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}},\mathit{\beta },\mathbf{\text{D}},\mathit{\lambda }\sim IG(\frac{N_k+{\tau }_k}{2},\frac{T_k+{\sum }_{i=1}^n{u}_i{\mathit{\mu }}_{ki}^{\top }{\mathit{\mu }}_{ki}}{2}),k=1,2,$$ (B-2)

where $N_1={\sum }_{i=1}^n{m}_{\mathit{\text{i}}}^P$, $N_2={\sum }_{i=1}^n{m}_{\mathit{\text{i}}}^C$, ${\mathit{\mu }}_{1i}={\mathbf{\text{y}}}_i^P-{\mathbf{\text{X}}}_i^P{\mathit{\beta }}^P-{\mathbf{\text{Z}}}_i^P{\mathbf{\text{b}}}_i^P$ and ${\mathit{\mu }}_{2i}={\mathbf{\text{y}}}_i^C-{\mathbf{\text{X}}}_i^C{\mathit{\beta }}^C-{\mathbf{\text{Z}}}_i^C{\mathbf{\text{b}}}_i^C$;

$$\mathit{\lambda }\mid \mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}},\mathit{\beta },{\sigma }_1^2,{\sigma }_2^2,\mathbf{\text{D}}\sim N({\sum }_{\mathbf{\Delta }}^{-1}{\mu }_{\mathbf{\Delta }},{\sum }_{\mathbf{\Delta }}^{-1}),$$ (B-3)

where ${\mathit{\mu }}_{\mathbf{\Delta }}={\mathbf{\text{S}}}_{\mathit{\lambda }}^{-1}{\mathit{\lambda }}_o+{\mathbf{\text{D}}}^{-1}{\sum }_{i=1}^n{u}_i{\mathbf{\text{b}}}_i$, ${\sum }_{\mathbf{\Delta }}={\mathbf{\text{D}}}^{-1}{\sum }_{i=1}^n{u}_i{t}_i^2+{\mathbf{\text{S}}}_{\mathit{\lambda }}^{-1}$;

$$\mathbf{\text{D}}\mid \mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}},\mathit{\beta },{\sigma }_1^2,{\sigma }_2^2,\mathit{\lambda }\sim I{W}_q{(({\mathbf{\text{T}}}_b^{-1}+\sum _{i=1}^n{u}_i({\mathbf{\text{b}}}_i-\mathbf{\Lambda }{\mathbf{\text{t}}}_i){({\mathbf{\text{b}}}_i-\mathbf{\Lambda }{\mathbf{\text{t}}}_i)}^{\top })}^{-1},{\tau }_b+n);$$ (B-4)

$${\mathbf{\text{b}}}_i\mid u_i,{\mathbf{\text{t}}}_i,\mathit{\beta },{\sigma }_1^2,{\sigma }_2^2,\mathbf{\text{D}},\mathit{\lambda }\sim N_q({\mathbf{\text{A}}}_{bi}^{-1}{\mathbf{\text{a}}}_i,u_i^{-1}{\mathbf{\text{A}}}_{bi}^{-1}),$$ (B-5)

where ${\mathbf{\text{A}}}_{bi}=({\mathbf{\text{Z}}}_i^{\top }{\sum }_i^{-1}{\mathbf{\text{Z}}}_i+{\mathbf{\text{D}}}^{-1})$ and ${\mathbf{\text{a}}}_i={\mathbf{\text{Z}}}_i^{\top }{\sum }_i^{-1}({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta })+t_i{\mathbf{\text{D}}}^{-1}\mathbf{\Lambda }$, i = 1, … n;

$${\mathbf{\text{t}}}_i\mid \mathit{\beta },{\sigma }_1^2,{\sigma }_2^2,\mathbf{\text{D}},\mathit{\lambda },{\mathbf{\text{b}}}_i,u_i\sim T{N}_q({\mathbf{\text{A}}}_t^{-1}{\mathbf{\text{a}}}_{ti},u_i^{-1}{\mathbf{\text{A}}}_t^{-1};{ℝ}_{+}^q),$$ (B-6)

where A_t = (I_q + Λ^⊤D⁻¹Λ), a_ti = Λ^⊤D⁻¹b_i.

Conditional posteriors for specific SNI cases follows.

• The ST distribution

  The density of the conditional posterior distribution takes the form:

  $$u_i\mid \mathit{\theta },\mathbf{\text{b}},\mathbf{\text{t}},\mathbf{\text{y}}\sim \text{Gamma}((n_i+2q+\nu )/2;\nu /2+C_i/2),$$

  where $C_i={({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta }-{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i)}^{\top }{\sum }_i^{-1}({\mathbf{\text{y}}}_i-{\mathbf{\text{X}}}_i\mathit{\beta }-{\mathbf{\text{Z}}}_i{\mathbf{\text{b}}}_i)+{({\mathbf{\text{b}}}_i-\mathbf{\Lambda }{\mathbf{\text{t}}}_i)}^{\top }{\mathbf{\text{D}}}^{-1}({\mathbf{\text{b}}}_i-\mathbf{\Lambda }{\mathbf{\text{t}}}_i)+{\mathbf{\text{t}}}_i^{\top }{\mathbf{\text{t}}}_i$.

  The full conditional posterior density of ν is:

  $$\pi (\nu \mid {\mathit{\theta }}_{(-\nu )},\mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}},\mathbf{\text{y}})\propto {\pi }_1(\nu )\times \text{Gamma}(\frac{n\nu }{2}+1,\frac{1}{2}\sum _{i=1}^n(u_i-log{u}_i)+\varrho ){\mathbb{\text{I}}}_{\{(2,\infty )\}},$$

  where π₁(ν) = (2^ν/2Γ(ν/2))⁻ⁿ, which does not have a closed form but a Metropolis-Hastings or rejection sampling step can be utilized to obtain draws from ν.

• The SSL distribution

  In this case, the full conditional posterior density of each u_i is:

  $$u_i\mid \mathit{\theta },\mathbf{\text{b}},\mathbf{\text{t}},\mathbf{\text{y}}\sim \text{Gamma}((n_i+2q+2\nu )/2;C_i/2){\mathbb{\text{I}}}_{\{(0,1)\}}(\nu )$$

  and the conditional posterior density of ν is

  $$\nu \mid {\mathit{\theta }}_{(-\nu )},\mathbf{\text{t}},\mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{y}}\sim \text{Gamma}(n+a,b-\sum _{i=1}^{n}log{u}_i)){\mathbb{\text{I}}}_{\{(0,\infty )\}}(\nu ).$$

• The SCN distribution

  The full conditional posterior of the proportion of outliers ν₁ is:

  $${\nu }_1\mid {\mathit{\theta }}_{(-{\nu }_1)},\mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}},\mathbf{\text{y}},{\nu }_2\sim \text{Beta}\left(a+\frac{n-{\sum }_{i=1}^n{u}_i}{1-{\nu }_2};b+\frac{{\sum }_{i=1}^n{u}_i-n{\nu }_2}{1-{\nu }_2}\right)$$

  and the conditional posterior density of ν₂ is:

  $$\pi ({\nu }_2\mid \mathit{\theta },\mathbf{\text{b}},\mathbf{\text{u}},\mathbf{\text{t}},\mathbf{\text{y}},{\nu }_1)\propto {\nu }_1^{(\frac{n-{\sum }_{i=1}^n{u}_i}{1-{\nu }_2})}\times {(1-{\nu }_1)}^{(\frac{{\sum }_{i=1}^n{u}_i-n{\nu }_2}{1-{\nu }_2})}.$$

  Similarly, a Metropolis–Hastings proposal [12] can be used to update ν₂.