Bayesian Meta-Analysis of Papanicolaou Smear Accuracy

Abstract

Objective

To perform a Bayesian analysis of data from a previous meta-analysis of Papanicolaou (Pap) smear accuracy (Fahey et al. Am J Epidemiol 1995; 141:680–689) and compare the results.

Methods

We considered two Bayesian models for the same dataset used in the Fahey et al study. Model I was a beta-binomial model which considered the number of true positives and false negatives as independent binomial random variables with probability parameters β (sensitivity) and a (one minus specificity), respectively. We assumed that β and a are independent, each following a beta distribution with exponential priors. Model II considered sensitivity and specificity jointly through a bivariate normal distribution on the logits of the sensitivity and specificity. We performed sensitivity analysis to examine the effect of prior selection on the parameter estimates.

Results

We compared the estimates of average sensitivity and specificity from the Bayesian models with those from Fahey et al.’s SROC approach. Model I produced results similar to those of the SROC approach. Model II produced point estimates higher than those of the SROC approach, although the credible intervals overlapped and were wider. Sensitivity analysis showed that the Bayesian models are somewhat sensitive to the variance of the prior distribution, but their point estimates are more robust than those of the SROC approach.

Conclusions

The Bayesian approach has advantages over the SROC approach in that it accounts for between-study variation and allows for estimating the sensitivity and specificity for a particular trial, taking into consideration the results of other trials, i.e., “borrowing strength” from other trials.

INTRODUCTION

The Papanicolaou (Pap) smear, which involves the collection, preparation, and examination of exfoliated cervical cells, is a medical procedure commonly used to screen for and diagnose cervical cancer. The Pap smear is believed to be a key strategy in the early detection and prevention of cervical cancer, and its accuracy has been the subject of many clinical trials and research papers. However, the results and conclusions of these trials and papers differ greatly. Fahey et al. [1] noted that among the studies included in their meta-analysis, the estimates of sensitivity and specificity ranged from 0.14 to 0.97 and from 0.11 to 0.99, respectively. In addition, study quality and other characteristics, including sample size and patients’ ages and races, also varied among the studies. These disparities warrant a systematic review of these studies. Here, we conduct such a systematic review through meta-analysis, a statistical technique that quantitatively pools the results of multiple independent studies to draw inferences from those studies.

The summary receiver operating characteristic (SROC) method, introduced by Littenberg and Moses [2,3], has been widely used by authors of published meta-analyses that examine diagnostic test accuracy. However, the SROC method has some inherent limitations that could affect its validity and usefulness. First, the SROC method is not based on a formal probability model; in fact, Littenberg and Moses call it a “data-analytic approach”[2]. Second, there are difficulties in dealing with any zeroes that appear in any cells of the 2×2 table used in diagnostic test evaluation, i.e. true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN). The continuity correction method, i.e., adding one half to each count in calculating the true-positive rate and the false-positive rate, introduces non-negligible downward bias to the estimated SROC curve [2,3,4]. An additional problem with the SROC method is that confidence intervals are based on large sample theory approximations and the appropriate sample size for a meta-analysis is the number of studies which may not be large enough for the approximation to be accurate.

In this paper we consider a Bayesian approach to assess the diagnostic test accuracy of multiple studies. We propose two Bayesian models, a beta-binomial model and a normal logit model, and compare the results to the SROC model.

METHODS

Study sources

We used the same primary studies as used in the meta-analysis by Fahey et al.[1]. All primary studies were published between January 1984 and March 1992, inclusive, and were identified by a MEDLINE search. In addition, manual searches of relevant journals, reference lists of retrieved articles, and communication with other researchers identified additional sources of published data. Three content areas were used for the literature search: cervical cancer/disease, tests for cervical abnormality, and test evaluation. Studies were excluded if they were not published in English, were review articles, or without original data. Also excluded were articles that did not use Pap smears, did not use histology as the reference standard, or did not report sufficient data for estimation of operating characteristics. There were 58 cross-sectional studies identified (Fahey et al.[1], Appendix 1, p. 687) that evaluated the Pap smear, used histology as the reference standard, and used a threshold of cervical intraepithelial neoplasia grade 1 (CIN1) or grade 2 (CIN2) or equivalent. In 31 of these studies, the Pap smear was used as a follow-up to prior abnormal tests; in the remaining 27 studies, the Pap smear was used for screening purposes.

Model I: Beta-binomial model

In the beta-binomial model, the number of true positives is a binomially distributed random number that has the true study-specific sensitivity (β) as a probability parameter:TP ~ bin (TP + FN, β). Similarly, the number of false positives is binomially distributed with the study-specific probability parameter a, which is equal to one minus specificity: FP ~ bin (FP + TN, α). It is assumed that the parameters β and a follow independent beta distributions with different parameters: β ~ beta (a₁, b₁) and α ~ beta (a₂, b₂). We place independent prior exponential distributions on a₁, b₁, a₂, and b₂. The particular parameters for all models can be found in Table 1. The goal is to choose prior values such that the prior means are close to the sample mean but have rather large variances, and hence are vague priors.

Table 1.

Prior parameters used in the Bayesian analyses.

Model I: Beta-binomial model	Model II :Normal logit model
a1 ~ exp(5)	θ ~ N(0,1000)
b1 ~ exp(3)	τ2 ~ InverseGamma(0.33,0.25)
a2 ~ exp(3)	μ ~ N(0,1000)
b2 ~ exp(5)	σ2 ~ InverseGamma(0.33,0.25)

Model II: Normal logit model

The aforementioned beta-binomial model (Model I) is relatively simple. However, it ignores possible correlation between sensitivity and specificity by independently modeling TP and FP. Model II, the normal logit model, includes correlation through the log odds ratio and is specified as follows:

$$\begin{array}{c}\mathit{\text{TP}}~\mathit{\text{bin}}(\mathit{\text{TP}}+\mathit{\text{FN}},\beta )\hfill \\ \mathit{\text{FP}}~\mathit{\text{bin}}(\mathit{\text{FP}}+\mathit{\text{TN}},\alpha )\hfill \\ \delta =\text{logit}(\beta )-\text{logit}\left(\alpha \right)\hfill \\ \text{logit}\left(\alpha \right)~N(\mu ,{\sigma }^2)\hfill \\ \delta ~N(\theta ,{\tau }^2)\hfill \end{array}$$

Here, logit (α) = log(α/(1- α)). The parameter δ denotes the log odds ratio for a given study. A preliminary analysis showed that it is reasonable to assume that δ follows a normal distribution, say N(θ, τ²) with mean ? and varianceτ². The correlation is modeled through δ, in particular the correlation between β and a is s/(s²+t²)^1/2. The parameters of the sampling model are μ, s², ?, and t². We assume independent normal and inverse gamma priors for the mean and variance parameters, respectively, for mathematical simplicity.

Model fitting

We fit each of the two models described in Table 1 in WinBUGS 1.4.1 [8] to the datasets consisting of the two subgroups (i.e. the 31 studies that concerned tests for follow-up purposes and the 27 studies that concerned tests for screening purposes). We ran 15,000 WinBUGS steps for each model. Here, we report the summary statistics after discarding the first 5000 “burn-in” samples.

Sensitivity Analysis

It is important to conduct a sensitivity analysis to determine how the choice of prior distributions affects the performance of a Bayesian model. To this end, we chose some representative priors that give large, intermediate, or small between-study heterogeneity, and compared the performances of the models using these different priors. If the performances differ very little, then we would conclude there is robustness against the choice of prior distributions.

RESULTS

Table 2 shows the Bayesian posterior estimates, using the specified prior parameters, of mean sensitivity and specificity for the 31 follow-up and 27 screening studies, and the 95% credible intervals based on posterior estimates of the standard errors. The estimates among the Bayesian models are clearly comparable. Model I has approximately the same estimates and interval widths as the SROC model of Fahey et al.[1] Model II yields higher point estimates for sensitivity and specificity. The 95% credible intervals for Model II are wider than the 95% confidence intervals determined in the SROC analysis by Fahey et al.[1] In addition, the interval estimates for specificity are shifted, consistent with the higher point estimates.

Table 2.

Bayesian posterior estimates of mean sensitivity and specificity. Entries in table are the means followed by the 95% credible intervals for the Bayesian Models I and II and 95% confidence intervals for the SROC Model (Fahey et al.[1]). Prior distribution for models I and II are specified in Table 1.

Model	Description	Sensitivity		Specificity
		Screening	Follow-up	Screening	Follow-up
Model I	Beta binomial	0.58 (0.49, 0.67)	0.65 (0.57, 0.72)	0.70 (0.62, 0.77)	0.68 (0.60, 0.75)
Model II	Normal logit	0.60 (0.45, 0.74)	0.69 (0.58, 0.79)	0.76 (0.66, 0.76)	0.73 (0.63, 0.81)
SROC	Summary ROC	0.58 (0.49, 0.67)	0.66 (0.58, 0.73)	0.69 (0.62, 0.77)	0.66 (0.58, 0.73)

We performed sensitivity analyses to examine the effect of prior distribution selection on the parameter estimates. In Tables 3 and 4, we show the results of such sensitivity analyses for Model I and II, respectively. Three sets of prior distributions were analyzed for each model. The estimated mean sensitivity and specificity for each model using different parameters are very close to each other.

Table 3.

Sensitivity analysis for Model I.

Prior parameter values	Sensitivity		Specificity
	Screening	Follow-up	Screening	Follow-up
a1 ~ exp(1); b1 ~ exp(1)	0.58 (0.48, 0.67)	0.64 (0.56, 0.72)	0.69 (0.60, 0.77)	0.67 (0.59, 0.75)
a2 ~ exp(1); b2 ~ exp(1)
a1 ~ exp(3); b1 ~ exp(5)	0.58 (0.49, 0.67)	0.65 (0.57, 0.72)	0.70 (0.62, 0.77)	0.68 (0.60, 0.75)
a2 ~ exp(5); b2 ~ exp(3)
a1 ~ exp(1); b1 ~ exp(2)	0.58 (0.48, 0.67)	0.64 (0.56, 0.72)	0.69 (0.60, 0.77)	0.67 (0.59, 0.74)
a2 ~ exp(2); b2 ~ exp(1)

Table 4.

Sensitivity analysis for Model II.

Prior parameter values	Sensitivity		Specificity
	Screening	Follow-up	Screening	Follow-up
θ ~ N(0,1000); μ ~ N(0,1000)	0.60 (0.45, 0.74)	0.69 (0.58, 0.79)	0.76 (0.66, 0.84)	0.73 (0.64, 0.81)
τ2 ~ IG(0.333,0.25); σ2 ~ IG(0.333,0.25)
θ ~ N(3.0,1000); μ ~ N(−2.2,1000)	0.60 (0.45, 0.74)	0.69 (0.58, 0.80)	0.76 (0.66, 0.84)	0.73 (0.63, 0.81)
τ2 ~ IG(0.333,0.75); σ2 ~ IG(0.333,0.75)
θ ~ N(3.0,1.0); μ ~ N(−2.2,1.0)	0.60 (0.46, 0.74)	0.69 (0.57, 0.79)	0.74 (0.68, 0.85)	0.74 (0.65, 0.82)
τ2 ~ IG(0.333,0.25); σ2 ~ IG(0.333,0.25)

Note: IG = Inverse Gamma

DISCUSSION

Many authors of meta-analyses that examine diagnostic test accuracy have used the summary receiver operating characteristic (SROC) approach [1,5,6], but confusion remains as to how to apply and interpret the resulting curves. Fahey et al. [1] and Sutton et al. [6] claimed that the advantage of the SROC curve used in this framework was that it could better account for the possibility that different studies used different test thresholds. However, both sources did not clearly discuss how this effect is accounted for. A non-significant slope was obtained in fitting the SROC curve; hence both sources concluded that the test threshold did not affect the test accuracy based on their analysis. The Model II used here does provide some flexibility in dealing with varying thresholds. If the threshold for a positive test result is increased, then both the true positive rates and false positive rates will go down, so d will not change much whereas a will decrease. Thus, if our posterior estimate for t² is small but for s² is large, this would be indicative that much of the variability may be due to varying thresholds. Model I does not lend itself to such clearly modeling of varying thresholds, but it is flexible enough to be able to accommodate such variation.

We proposed Bayesian models as alternatives to the SROC approach in the meta-analysis of diagnostic test accuracy. Although the models here were applied to Pap smear studies, they can be used with similar outcomes for other diagnostic tests. With the proper selection of priors, Bayesian models can account for between-study heterogeneity other than from varying thresholds for a positive test. Bayesian models provide posterior estimates for each individual study while taking into consideration the results of other studies, or “borrowing strength” from other studies. We believe that Bayesian models provide a more realistic and flexible framework in which to combine studies and integrate information in meta-analysis.

In our analysis, the two Bayesian model realizations gave similar results in terms of estimation of the mean sensitivity and specificity. For the follow-up group, all these models estimated a mean sensitivity and specificity smaller than that of the weighted mean from Mitchell et al. [5] (0.57–0.67 vs. 0.75, and 0.66–0.68 vs. 0.73, respectively). It is also interesting that the screening group had a lower estimated sensitivity but a higher specificity than did the follow-up group. This may be because of different test thresholds used. When screening healthy individuals, doctors tend to require higher levels of abnormality to claim a diseased case, hence lower sensitivity but higher specificity. But when performing follow-up tests for patients with prior abnormal Pap smear results, doctors are more likely to use a less stringent threshold of abnormality to claim a test result is “positive.” These differences may also have to do with fundamental differences in the population. It is natural to expect that in the screening group, there are more clear negatives and more borderline positives, hence higher true negative and false negative rates.

Despite the fact that the two Bayesian models gave similar mean estimates, the normal logit model makes more intuitive sense because sensitivity and specificity are correlated. Furthermore, this model is better than the beta-binomial model, because it allows more between-study heterogeneity. In our analysis, the normal logit model produced higher point estimates for both sensitivity and specificity. Further study will determine whether this is a true reflection of reality.

We recognize that these estimates should be viewed with caution. As pointed out by Fahey et al.,[1] the estimates of the positivity rate of Pap smear screening is approximately 5–10 percent. However, the best operating characteristics as calculated above (sensitivity of 0.60 and specificity of 0.76) would yield a positivity rate no less than 24 percent. Thus, the true estimate for specificity for the Pap smear is probably in the upper end of the confidence or credible interval, i.e. closer to 0.90, which is consistent with estimates used in published decision-analytic models for cervical cancer screening [7]. It is clear that the data used in this analysis is somewhat inconsistent with result, which is based on very large data sets. A further advantage of the Bayesian approach is that it can incorporate incomplete information such as simply a positivity rate, or results of follow up tests applied only to the subset of patients who have a positive Pap smear.

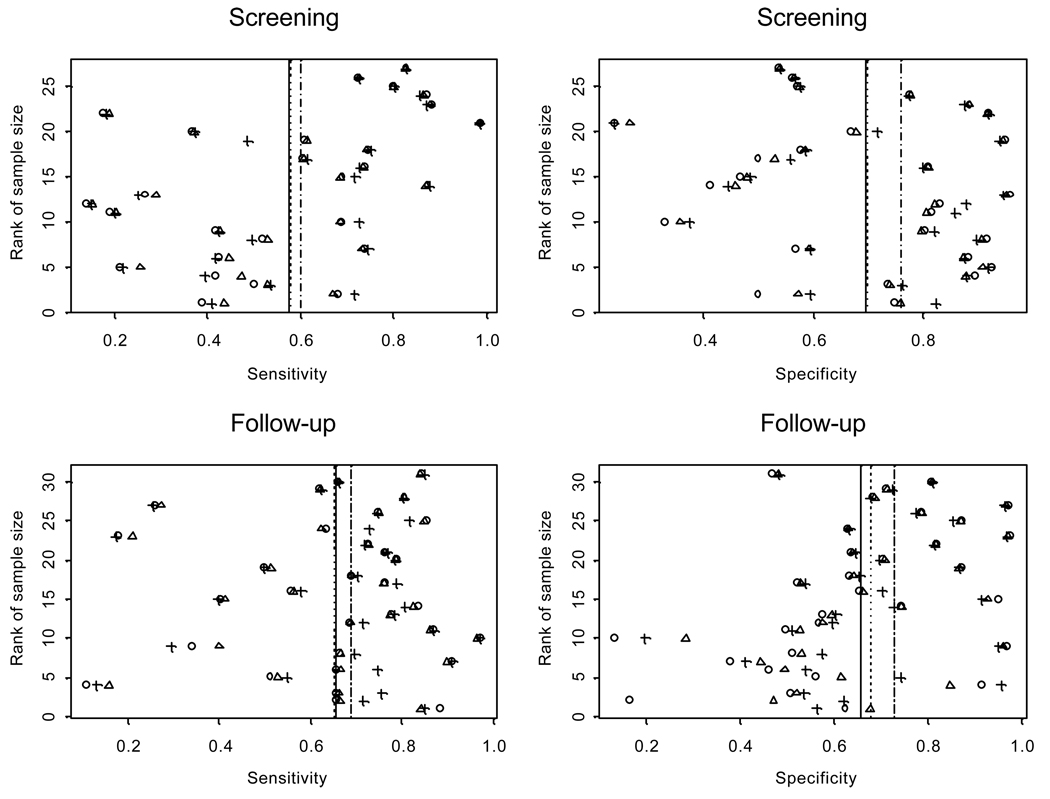
Figure 1.

Estimated sensitivity and specificity for individual studies. On each panel, circles are the estimated value from observed data; triangles for Model I and crosses for Model II. Solid vertical lines are the means estimated from observed data; dotted lines are the means estimated from Model I and dashed line from Model II. The two Bayesian models used prior parameters specified in Table 1.