Abstract
The title complex, [Fe(C6H4N5)2(H2O)2], was synthesized by the reaction of ferrous sulfate with 5-(2-pyridyl)-2H-tetrazole (HL). The FeII atom, located on a crystallographic center of inversion, is coordinated by four N-atom donors from two planar trans-related deprotonated L ligands and two O atoms from two axial water molecules in a distorted octahedral geometry. The FeII mononuclear units are further connected by intermolecular O—H⋯N and C—H⋯O hydrogen-bonding interactions, forming a three-dimensional framework.
Related literature
For hydrogen bonds, see: Desiraju & Steiner (1999 ▶); Kitagawa & Uemura (2005 ▶); For general background, see: Rizk et al. (2005 ▶); Robin & Fromm (2006 ▶); For structurally related complexes with tetrazole ligands, see: Mo et al. (2004 ▶); Song et al. (2008 ▶); Tao et al. (2008 ▶); Wang et al. (2003 ▶); Wen (2008 ▶); Wu et al. (2007 ▶).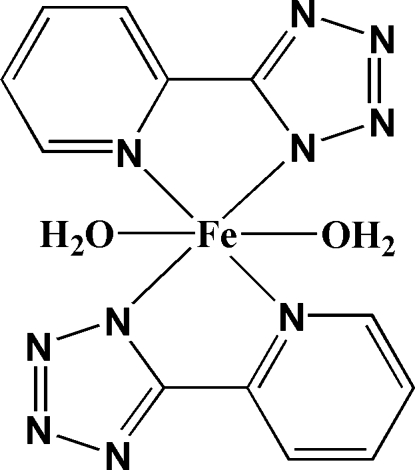
Experimental
Crystal data
[Fe(C6H4N5)2(H2O)2]
M r = 384.17
Monoclinic,
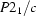
a = 8.114 (2) Å
b = 12.924 (3) Å
c = 7.360 (2) Å
β = 96.021 (3)°
V = 767.5 (3) Å3
Z = 2
Mo Kα radiation
μ = 1.02 mm−1
T = 293 K
0.29 × 0.14 × 0.11 mm
Data collection
Bruker SMART CCD area-detector diffractometer
Absorption correction: multi-scan (SADABS; Sheldrick, 1996 ▶) T min = 0.757, T max = 0.897
4287 measured reflections
1356 independent reflections
1204 reflections with I > 2σ(I)
R int = 0.017
Refinement
R[F 2 > 2σ(F 2)] = 0.023
wR(F 2) = 0.057
S = 1.10
1356 reflections
115 parameters
H-atom parameters constrained
Δρmax = 0.23 e Å−3
Δρmin = −0.24 e Å−3
Data collection: SMART (Bruker, 1998 ▶); cell refinement: SAINT (Bruker, 1998 ▶); data reduction: SAINT; program(s) used to solve structure: SHELXS97 (Sheldrick, 2008 ▶); program(s) used to refine structure: SHELXL97 (Sheldrick, 2008 ▶); molecular graphics: SHELXTL (Sheldrick, 2008 ▶); software used to prepare material for publication: SHELXTL and PLATON (Spek, 2009 ▶).
Supplementary Material
Crystal structure: contains datablocks I, global. DOI: 10.1107/S1600536809007892/im2104sup1.cif
Structure factors: contains datablocks I. DOI: 10.1107/S1600536809007892/im2104Isup2.hkl
Additional supplementary materials: crystallographic information; 3D view; checkCIF report
Table 1. Hydrogen-bond geometry (Å, °).
| D—H⋯A | D—H | H⋯A | D⋯A | D—H⋯A |
|---|---|---|---|---|
| O1—H11⋯N5i | 0.85 | 1.91 | 2.764 (2) | 177 |
| O1—H12⋯N4ii | 0.85 | 2.00 | 2.823 (2) | 162 |
| C2—H2⋯O1iii | 0.93 | 2.56 | 3.362 (3) | 145 |
Symmetry codes: (i) 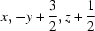 ; (ii)
; (ii) 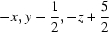 ; (iii)
; (iii) 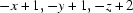 .
.
Acknowledgments
This work was supported by the Start-up Fund for PhDs in Natural Scientific Research of Zhengzhou University of Light Industry (grant No. 2006BSJJ001 to SMF). We also thank Dr Chun-Sen Liu for his helpful discussions and valuable suggestions.
supplementary crystallographic information
Comment
Currently, there is considerable interest in self-assembly and construction of supramolecular complexes featuring fascinating architectures realized by noncovalent interactions such as coordination bonds, hydrogen bonds and other weak intermolecular interactions (Rizk et al., 2005; Robin & Fromm, 2006). Hydrogen bonds, combining directionality, strength and selectivity, have been noted as the most versatile organizing force to assemble supramolecular structures (Kitagawa & Uemura, 2005). Due to their ability of providing multi-coordination sites as well as hydrogen bonding acceptors, tetrazole and its derivatives are receiving much attention in coordination and supramolecular chemistry (Mo et al., 2004; Song et al., 2008; Tao et al., 2008; Wang et al., 2003; Wen, 2008; Wu et al., 2007). Herein we report the crystal structure of an iron(II) complex of 2-pyridyl-tetrazole HL, [Fe(L)2(H2O)2].
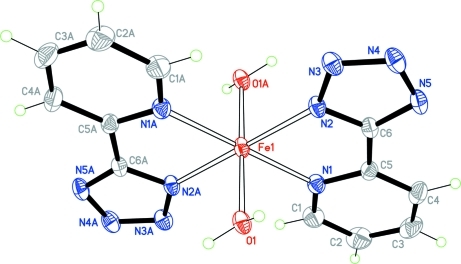
In the title complex, the FeII atom is located on a crystallographic center of inversion. It is six-coordinated by two O atoms from water molecules and four N-atom donors from two deprotonated N,N'-chelating L ligands binding via the pyridyl nitrogen and the tetrazole nitrogen in 1-position, in a transoid pseudo-octahedral geometry (Fig. 1).
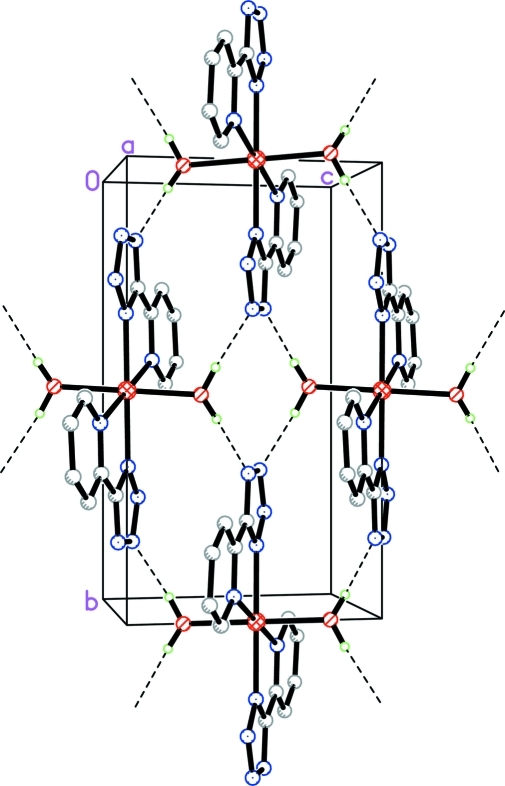
Each FeII mononuclear unit exhibits both proton donors (water molecules) and acceptors (uncoordinated N atoms on the tetrazole rings) and can therefore act as a good building unit for hydrogen bonded networks. As shown in Fig. 2 the O—H···N hydrogen bonds (Table 1) between tetrazole rings and coordinated water molecules link neighboring mononuclear [Fe(L)2(H2O)2] units resulting in an infinite hydrogen bonded layer running parallel to the crystallographic (100) plane. Furthermore, the crystal structure of (I) also contains intermolecular C—H···O (Table 1) hydrogen-bonding interactions (Desiraju & Steiner, 1999), between the L ligands and the coordinated water molecules that interlink the twodimensional layers to form a three dimensional supramolecular framework.
Experimental
A solution of HL (0.05 mmol) in CH3OH (10 ml) in the presence of excess 2,6-dimethylpyridine (ca 0.05 ml for adjusting the pH value of the reaction system to basic conditions) was carefully layered on top of an aqueous solution (15 ml) of FeSO4 (0.1 mmol) in a test tube. Yellow single crystals suitable for X-ray analysis appeared at the tube wall after ca one month at room temperature (yield ~30% based on HL). Elemental analysis calculated for (C12H12FeN10O2): H 3.15, C 37.52, N 36.46%; found: H 3.08, C 37.37, N 36.68%.
Refinement
H atoms of the water molecules were located from the difference Fourier map and were allowed to ride on the O atom, with Uiso(H) = 1.2 Ueq(O). The remaining H atoms were included in calculated positions and treated in the subsequent refinement as riding atoms, with C—H = 0.93 (aromatic), and Uiso(H) = 1.2 Ueq(C).
Figures
Fig. 1.
The molecular structure of the title complex. Displacement ellipsoids are drawn at the 30% probability level. Atoms labelled with the suffix A are generated by the symmetry operation (–x, –y + 1,–z + 2).
Fig. 2.
Two dimensional network, parallel to the (100) plane, formed by the intermolecular O—H···N (fine dashed lines) interactions. For clarity, only H atoms involved in the interactions are shown.
Crystal data
| [Fe(C6H4N5)2(H2O)2] | F(000) = 392 |
| Mr = 384.17 | Dx = 1.662 Mg m−3 |
| Monoclinic, P21/c | Mo Kα radiation, λ = 0.71073 Å |
| Hall symbol: -P 2ybc | Cell parameters from 2211 reflections |
| a = 8.114 (2) Å | θ = 3.0–28.3° |
| b = 12.924 (3) Å | µ = 1.01 mm−1 |
| c = 7.360 (2) Å | T = 293 K |
| β = 96.021 (3)° | Block, yellow |
| V = 767.5 (3) Å3 | 0.29 × 0.14 × 0.11 mm |
| Z = 2 |
Data collection
| Bruker SMART CCD area-detector diffractometer | 1356 independent reflections |
| Radiation source: fine-focus sealed tube | 1204 reflections with I > 2σ(I) |
| graphite | Rint = 0.017 |
| φ and ω scans | θmax = 25.0°, θmin = 3.0° |
| Absorption correction: multi-scan (SADABS; Sheldrick, 1996) | h = −9→8 |
| Tmin = 0.757, Tmax = 0.897 | k = −15→15 |
| 4287 measured reflections | l = −8→8 |
Refinement
| Refinement on F2 | Primary atom site location: structure-invariant direct methods |
| Least-squares matrix: full | Secondary atom site location: difference Fourier map |
| R[F2 > 2σ(F2)] = 0.023 | Hydrogen site location: inferred from neighbouring sites |
| wR(F2) = 0.057 | H-atom parameters constrained |
| S = 1.10 | w = 1/[σ2(Fo2) + (0.0207P)2 + 0.3154P] where P = (Fo2 + 2Fc2)/3 |
| 1356 reflections | (Δ/σ)max < 0.001 |
| 115 parameters | Δρmax = 0.23 e Å−3 |
| 0 restraints | Δρmin = −0.24 e Å−3 |
Special details
| Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell e.s.d.'s are taken into account individually in the estimation of e.s.d.'s in distances, angles and torsion angles; correlations between e.s.d.'s in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s. planes. |
| Refinement. Refinement of F2 against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F2, conventional R-factors R are based on F, with F set to zero for negative F2. The threshold expression of F2 > σ(F2) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F2 are statistically about twice as large as those based on F, and R- factors based on ALL data will be even larger. |
Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Å2)
| x | y | z | Uiso*/Ueq | ||
| Fe1 | 0.0000 | 0.5000 | 1.0000 | 0.02908 (12) | |
| C1 | 0.3360 (2) | 0.51552 (16) | 0.8123 (3) | 0.0456 (5) | |
| H1 | 0.3306 | 0.4437 | 0.8065 | 0.055* | |
| C2 | 0.4708 (3) | 0.56508 (19) | 0.7511 (3) | 0.0565 (6) | |
| H2 | 0.5543 | 0.5270 | 0.7050 | 0.068* | |
| C3 | 0.4800 (3) | 0.67167 (19) | 0.7593 (3) | 0.0539 (6) | |
| H3 | 0.5708 | 0.7063 | 0.7213 | 0.065* | |
| C4 | 0.3524 (2) | 0.72590 (16) | 0.8246 (3) | 0.0440 (5) | |
| H4 | 0.3550 | 0.7978 | 0.8296 | 0.053* | |
| C5 | 0.2204 (2) | 0.67171 (13) | 0.8826 (2) | 0.0318 (4) | |
| C6 | 0.0757 (2) | 0.72097 (12) | 0.9502 (2) | 0.0304 (4) | |
| N1 | 0.21327 (18) | 0.56715 (11) | 0.87949 (19) | 0.0332 (3) | |
| N2 | −0.04622 (17) | 0.66384 (10) | 1.00861 (18) | 0.0308 (3) | |
| N3 | −0.15883 (19) | 0.73201 (11) | 1.0590 (2) | 0.0367 (4) | |
| N4 | −0.1046 (2) | 0.82582 (11) | 1.0311 (2) | 0.0396 (4) | |
| N5 | 0.0442 (2) | 0.82160 (11) | 0.9625 (2) | 0.0375 (4) | |
| O1 | 0.13384 (15) | 0.50897 (8) | 1.26584 (16) | 0.0340 (3) | |
| H11 | 0.1091 | 0.5606 | 1.3292 | 0.041* | |
| H12 | 0.1461 | 0.4509 | 1.3199 | 0.041* |
Atomic displacement parameters (Å2)
| U11 | U22 | U33 | U12 | U13 | U23 | |
| Fe1 | 0.0345 (2) | 0.01947 (19) | 0.0352 (2) | 0.00073 (14) | 0.01281 (15) | 0.00110 (14) |
| C1 | 0.0410 (11) | 0.0464 (12) | 0.0517 (12) | 0.0074 (9) | 0.0153 (9) | 0.0027 (9) |
| C2 | 0.0407 (13) | 0.0745 (16) | 0.0573 (13) | 0.0099 (11) | 0.0195 (10) | 0.0056 (12) |
| C3 | 0.0357 (11) | 0.0773 (17) | 0.0497 (12) | −0.0136 (11) | 0.0102 (9) | 0.0086 (11) |
| C4 | 0.0444 (12) | 0.0457 (11) | 0.0423 (10) | −0.0154 (9) | 0.0069 (9) | 0.0037 (9) |
| C5 | 0.0352 (9) | 0.0332 (10) | 0.0268 (8) | −0.0052 (7) | 0.0020 (7) | 0.0027 (7) |
| C6 | 0.0409 (10) | 0.0249 (9) | 0.0253 (8) | −0.0037 (7) | 0.0028 (7) | 0.0007 (7) |
| N1 | 0.0343 (8) | 0.0313 (8) | 0.0355 (8) | 0.0010 (6) | 0.0099 (6) | 0.0028 (6) |
| N2 | 0.0378 (8) | 0.0215 (7) | 0.0346 (8) | 0.0018 (6) | 0.0103 (6) | −0.0002 (6) |
| N3 | 0.0449 (9) | 0.0274 (8) | 0.0390 (8) | 0.0062 (7) | 0.0091 (7) | −0.0022 (6) |
| N4 | 0.0564 (10) | 0.0255 (8) | 0.0371 (8) | 0.0046 (7) | 0.0064 (7) | −0.0017 (6) |
| N5 | 0.0543 (10) | 0.0223 (7) | 0.0358 (8) | −0.0032 (7) | 0.0040 (7) | 0.0015 (6) |
| O1 | 0.0434 (7) | 0.0226 (6) | 0.0373 (7) | 0.0035 (5) | 0.0105 (5) | 0.0006 (5) |
Geometric parameters (Å, °)
| Fe1—O1i | 2.1389 (13) | C3—H3 | 0.9300 |
| Fe1—O1 | 2.1389 (13) | C4—C5 | 1.384 (2) |
| Fe1—N2 | 2.1526 (14) | C4—H4 | 0.9300 |
| Fe1—N2i | 2.1526 (14) | C5—N1 | 1.353 (2) |
| Fe1—N1i | 2.2037 (14) | C5—C6 | 1.468 (2) |
| Fe1—N1 | 2.2037 (14) | C6—N5 | 1.330 (2) |
| C1—N1 | 1.336 (2) | C6—N2 | 1.341 (2) |
| C1—C2 | 1.383 (3) | N2—N3 | 1.3489 (19) |
| C1—H1 | 0.9300 | N3—N4 | 1.313 (2) |
| C2—C3 | 1.380 (3) | N4—N5 | 1.358 (2) |
| C2—H2 | 0.9300 | O1—H11 | 0.8501 |
| C3—C4 | 1.378 (3) | O1—H12 | 0.8500 |
| O1i—Fe1—O1 | 180.0 | C2—C3—H3 | 120.5 |
| O1i—Fe1—N2 | 90.40 (5) | C3—C4—C5 | 118.96 (19) |
| O1—Fe1—N2 | 89.60 (5) | C3—C4—H4 | 120.5 |
| O1i—Fe1—N2i | 89.60 (5) | C5—C4—H4 | 120.5 |
| O1—Fe1—N2i | 90.40 (5) | N1—C5—C4 | 122.25 (17) |
| N2—Fe1—N2i | 180.0 | N1—C5—C6 | 113.85 (14) |
| O1i—Fe1—N1i | 90.12 (5) | C4—C5—C6 | 123.89 (16) |
| O1—Fe1—N1i | 89.88 (5) | N5—C6—N2 | 111.28 (15) |
| N2—Fe1—N1i | 103.24 (5) | N5—C6—C5 | 127.83 (15) |
| N2i—Fe1—N1i | 76.76 (5) | N2—C6—C5 | 120.89 (14) |
| O1i—Fe1—N1 | 89.89 (5) | C1—N1—C5 | 118.22 (16) |
| O1—Fe1—N1 | 90.11 (5) | C1—N1—Fe1 | 126.83 (13) |
| N2—Fe1—N1 | 76.76 (5) | C5—N1—Fe1 | 114.89 (11) |
| N2i—Fe1—N1 | 103.24 (5) | C6—N2—N3 | 105.81 (13) |
| N1i—Fe1—N1 | 180.000 (1) | C6—N2—Fe1 | 113.29 (11) |
| N1—C1—C2 | 122.33 (19) | N3—N2—Fe1 | 140.87 (11) |
| N1—C1—H1 | 118.8 | N4—N3—N2 | 108.19 (14) |
| C2—C1—H1 | 118.8 | N3—N4—N5 | 110.28 (13) |
| C3—C2—C1 | 119.3 (2) | C6—N5—N4 | 104.44 (14) |
| C3—C2—H2 | 120.4 | Fe1—O1—H11 | 114.7 |
| C1—C2—H2 | 120.4 | Fe1—O1—H12 | 113.8 |
| C4—C3—C2 | 118.92 (19) | H11—O1—H12 | 117.3 |
| C4—C3—H3 | 120.5 | ||
| N1—C1—C2—C3 | 0.0 (3) | N2—Fe1—N1—C5 | 5.08 (12) |
| C1—C2—C3—C4 | −1.4 (3) | N2i—Fe1—N1—C5 | −174.92 (12) |
| C2—C3—C4—C5 | 1.0 (3) | N5—C6—N2—N3 | 0.17 (19) |
| C3—C4—C5—N1 | 0.8 (3) | C5—C6—N2—N3 | −179.46 (14) |
| C3—C4—C5—C6 | −178.37 (17) | N5—C6—N2—Fe1 | −178.30 (11) |
| N1—C5—C6—N5 | −177.20 (16) | C5—C6—N2—Fe1 | 2.07 (19) |
| C4—C5—C6—N5 | 2.1 (3) | O1i—Fe1—N2—C6 | −93.43 (12) |
| N1—C5—C6—N2 | 2.4 (2) | O1—Fe1—N2—C6 | 86.57 (12) |
| C4—C5—C6—N2 | −178.36 (16) | N1i—Fe1—N2—C6 | 176.36 (11) |
| C2—C1—N1—C5 | 1.8 (3) | N1—Fe1—N2—C6 | −3.64 (11) |
| C2—C1—N1—Fe1 | −175.34 (15) | O1i—Fe1—N2—N3 | 88.90 (18) |
| C4—C5—N1—C1 | −2.2 (3) | O1—Fe1—N2—N3 | −91.10 (18) |
| C6—C5—N1—C1 | 177.07 (16) | N1i—Fe1—N2—N3 | −1.31 (18) |
| C4—C5—N1—Fe1 | 175.23 (13) | N1—Fe1—N2—N3 | 178.69 (18) |
| C6—C5—N1—Fe1 | −5.48 (18) | C6—N2—N3—N4 | −0.01 (18) |
| O1i—Fe1—N1—C1 | −87.30 (16) | Fe1—N2—N3—N4 | 177.76 (13) |
| O1—Fe1—N1—C1 | 92.70 (16) | N2—N3—N4—N5 | −0.15 (19) |
| N2—Fe1—N1—C1 | −177.74 (17) | N2—C6—N5—N4 | −0.26 (19) |
| N2i—Fe1—N1—C1 | 2.26 (17) | C5—C6—N5—N4 | 179.35 (16) |
| O1i—Fe1—N1—C5 | 95.51 (12) | N3—N4—N5—C6 | 0.25 (19) |
| O1—Fe1—N1—C5 | −84.49 (12) |
Symmetry codes: (i) −x, −y+1, −z+2.
Hydrogen-bond geometry (Å, °)
| D—H···A | D—H | H···A | D···A | D—H···A |
| O1—H11···N5ii | 0.85 | 1.91 | 2.764 (2) | 177 |
| O1—H12···N4iii | 0.85 | 2.00 | 2.823 (2) | 162 |
| C2—H2···O1iv | 0.93 | 2.56 | 3.362 (3) | 145 |
Symmetry codes: (ii) x, −y+3/2, z+1/2; (iii) −x, y−1/2, −z+5/2; (iv) −x+1, −y+1, −z+2.
Footnotes
Supplementary data and figures for this paper are available from the IUCr electronic archives (Reference: IM2104).
References
- Bruker (1998). SMART and SAINT Bruker AXS Inc., Madison, Wisconsin, USA.
- Desiraju, G. R. & Steiner, T. (1999). The Weak Hydrogen Bond in Structural Chemistry and Biology Oxford University Press.
- Kitagawa, S. & Uemura, K. (2005). Chem. Soc. Rev.34, 109–119. [DOI] [PubMed]
- Mo, X.-J., Gao, E.-Q., He, Z., Li, W.-J. & Yan, C.-H. (2004). Inorg. Chem. Commun.7, 353–355.
- Rizk, A. T., Kilner, C. A. & Halcrow, M. A. (2005). CrystEngComm, 7, 359–362.
- Robin, A. Y. & Fromm, K. M. (2006). Coord. Chem. Rev.250, 2127–2157.
- Sheldrick, G. M. (1996). SADABS University of Göttingen, Germany.
- Sheldrick, G. M. (2008). Acta Cryst. A64, 112–122. [DOI] [PubMed]
- Song, Y.-H., Chiu, Y.-C., Chi, Y., Chou, P.-T., Cheng, Y.-M., Lin, C.-W., Lee, G.-H. & Carty, A. J. (2008). Organometallics, 27, 80–87.
- Spek, A. L. (2009). Acta Cryst. D65, 148–155. [DOI] [PMC free article] [PubMed]
- Tao, Y., Li, J.-R., Yu, Q., Song, W.-C., Tong, X.-L. & Bu, X.-H. (2008). CrystEngComm, 10, 699–705.
- Wang, L.-Z., Qu, Z.-R., Zhao, H., Wang, X.-S., Xiong, R.-G. & Xue, Z.-L. (2003). Inorg. Chem.42, 3969–3971. [DOI] [PubMed]
- Wen, X.-C. (2008). Acta Cryst. E64, m768. [DOI] [PMC free article] [PubMed]
- Wu, L.-L., Yang, C.-H., Sun, I.-W., Chu, S.-Y., Kao, P.-C. & Huang, H.-H. (2007). Organometallics, 26, 2017–2023.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Crystal structure: contains datablocks I, global. DOI: 10.1107/S1600536809007892/im2104sup1.cif
Structure factors: contains datablocks I. DOI: 10.1107/S1600536809007892/im2104Isup2.hkl
Additional supplementary materials: crystallographic information; 3D view; checkCIF report