Monitoring ion-channel function in real time through quantum decoherence

Abstract

In drug discovery, there is a clear and urgent need for detection of cell-membrane ion-channel operation with wide-field capability. Existing techniques are generally invasive or require specialized nanostructures. We show that quantum nanotechnology could provide a solution. The nitrogen-vacancy (NV) center in nanodiamond is of great interest as a single-atom quantum probe for nanoscale processes. However, until now nothing was known about the quantum behavior of a NV probe in a complex biological environment. We explore the quantum dynamics of a NV probe in proximity to the ion channel, lipid bilayer, and surrounding aqueous environment. Our theoretical results indicate that real-time detection of ion-channel operation at millisecond resolution is possible by directly monitoring the quantum decoherence of the NV probe. With the potential to scan and scale up to an array-based system, this conclusion may have wide-ranging implications for nanoscale biology and drug discovery.

The cell membrane is a critical regulator of life. Its importance is reflected by the fact that the majority of drugs target membrane interactions (1). Ion channels allow for passive and selective diffusion of ions across the cell membrane (2), whereas ion pumps actively create and maintain the potential gradients across the membranes of living cells (3). To monitor the effect of new drugs and drug delivery mechanisms, a wide-field ion-channel monitoring capability is essential (4). However, there are significant challenges facing existing techniques stemming from the fact that membrane proteins, hosted in a lipid bilayer, require a complex environment to preserve their structural and functional integrity (1, 5–7). Patch clamp techniques are generally invasive, quantitatively inaccurate, and difficult to scale up (8, 9), whereas black lipid membranes (10, 11) often suffer from stability issues and can only host a limited number of membrane proteins.

Instead of altering the way ion channels and the lipid membrane are presented or even assembled for detection, our approach is to consider a unique and inherently noninvasive in situ detection method based on the quantum properties of a single-atom probe. The atomic probe is a single nitrogen-vacancy (NV) center in a nanodiamond crystal that is highly sensitive to magnetic fields and shows great promise as a magnetometer for nanobiosensing (12–19). The NV center in nanodiamond has already been used as a fluorescence marker in biological systems (20–24). However, up to now there has been no analysis of the effect of the biological environment on the quantum dynamics of the NV center—such considerations are critical to nanobiomagnetometry applications. We explore these issues in detail and, furthermore, show that the rate of quantum decoherence of the NV center is sufficiently sensitive to the flow of ions through the channel to allow real-time detection, over and above the myriad background effects. In this context, decoherence refers to the loss of quantum coherence between magnetic sublevels of the NV atomic system due to interactions with an environment. Such superpositions of quantum states are generally fleeting in nature due to interactions with the environment, and the degree and timescale over which such quantum coherence is lost can be measured precisely. The immediate consequence of the fragility of the quantum coherence phenomenon is that detecting the loss of quantum coherence (decoherence) in such a single-atom probe offers a unique monitor of biological function at the nanoscale (18, 19).

The NV probe (Fig. 1) consists of a diamond nanocrystal containing an NV defect at the end of an atomic force microscope tip, as recently demonstrated (16). For biological applications, a quantum probe must be submersible to be brought within nanometers of the sample structure, hence the NV system locked and protected in the ultrastable diamond matrix (Fig. 1A) is the system of choice. The NV center alone offers the controllable, robust, and persistent quantum properties such room temperature nanosensing applications will demand, as well as zero toxicity in a biological environment (20–22). Theoretical proposals for the use of diamond nanocrystals as sensitive nanoscale magnetometers (12–14) have been followed by proof-of-principle experiments (15–17). However, such nanoscale magnetometers employ only a fraction of the quantum resources at hand and do not have the sensitivity to detect the minute magnetic moment fluctuations associated with ion-channel operation. In contrast, our results show that measuring the quantum decoherence of the NV induced by the ion flux provides a highly sensitive monitoring capability for the ion-channel problem, well beyond the limits of magnetometer time-averaged field sensitivity (19). To determine the sensitivity of the NV probe to the ion-channel signal, we describe the lipid membrane, embedded ion channels, and the immediate surroundings as a fluctuating electromagnetic environment and quantitatively assess each effect on the quantum coherence of the NV center. We consider the diffusion of nuclei, atoms, and molecules in the immediate surroundings of the nanocrystal and the extent to which each source will decohere the quantum state of the NV. We find that, over and above these background sources, the decoherence of the NV spin levels is highly sensitive to the ion flux through a single ion channel. Our theoretical findings demonstrate the potential of this approach to revolutionize the way ion channels and potentially other membrane-bound proteins or interacting species are characterized and measured, particularly when scaleup and scanning capabilities are considered.

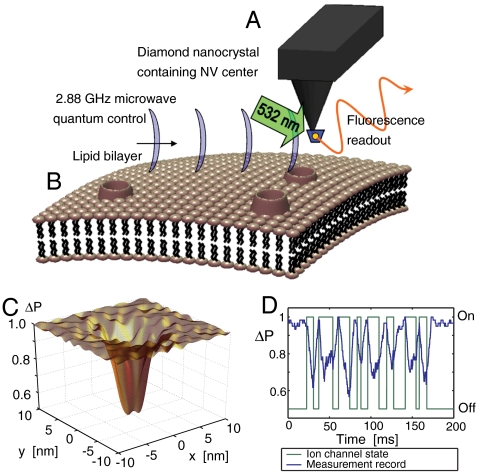
Fig. 1.

Quantum decoherence imaging of ion-channel operation (simulations). (A) A single NV defect in a diamond nanocrystal is placed on an atomic force microscope tip. The unique properties of the NV atomic level scheme allows for optically induced readout and microwave control of magnetic (spin) sublevels. (B) The nearby cell membrane is host to channels permitting the flow of ions across the surface. The ion motion results in an effective fluctuating magnetic field at the NV position which decoheres the quantum state of the NV system. (C) This decoherence results in a decrease in fluorescence, which is most pronounced in regions close to the ion-channel opening. (D) Changes in fluorescence also permit the temporal tracking of ion-channel dynamics.

This paper is organized as follows. We begin by describing the quantum decoherence imaging system (Fig. 1) implemented using an NV center in a realistic technology platform. The biological system is described in detail, and estimates of the sensitivity of the NV decoherence to various magnetic field sources are made that indicate the ability to detect ion-channel switch-on/off events. Finally, we conduct large-scale numerical simulations of the time evolution of the NV spin system, including all magnetic field generating processes, which acts to verify the analytic picture and provides quantitative results for the monitoring and scanning capabilities of the system.

Results

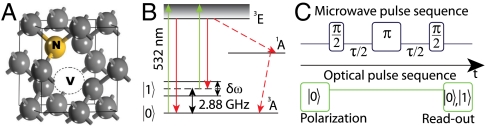
The energy level scheme of the C_3v-symmetric NV system (Fig. 2B) consists of ground (³A), excited (³E), and metastable (¹A) states. The ground-state manifold has spin sublevels (m = 0, ± 1), which in zero field are split by 2.88 GHz. In a background magnetic field, the lowest two states (m = 0, +1) are readily accessible by microwave control. An important property of the NV system is that, under optical excitation, the spin levels are distinguishable by a difference in fluorescence, hence spin-state readout is achieved by purely optical means (25, 26). These properties are fortuitous in the current context because mammalian ion-channel function is known to be insensitive to optical light (27). Because of the simple readout and control, the quantum properties of the NV system and the interaction with the immediate crystalline environment are well known (28, 29). The coherence time of the spin levels is very long even at room temperature: In type 1b nanocrystals T₂ ∼ 15 μs (30) and, in isotopically engineered diamond, can be as long as 1.8 ms (17) with the use of a spin-echo microwave control sequence (Fig. 2C). More encouraging is that these times are predicted to be as high as 75 μs and 100 ms, respectively, with the application of optimal microwave pulse sequences (31). Nanocrystals of 5-nm diameter containing stable NV centers have recently been demonstrated (32).

Fig. 2.

Details of the NV center structure, energy levels, and control scheme. (A) NV-center diamond lattice defect. (B) NV spin detection through optical excitation and emission cycle. Magnetic sublevels m_s = 0 and m_s =  ± 1 are split by a D = 2.88 GHz crystal field. Degeneracy between the m_s =  ± 1 sublevels is lifted by a Zeeman shift, δω. Application of 532 nm green light induces a spin-dependent photoluminescence and pumping into the m_s = 0 ground state. (C) Microwave and optical pulse sequences for coherent control and readout.

Typical ion-channel species K⁺, Ca²⁺, Na⁺, and nearby water molecules are electron spin paired, so any magnetic signal due to ion-channel operation will be primarily from the motion of nuclear spins. Ions and water molecules enter the channel in thermal equilibrium with random spin orientations and move through the channel over a microsecond timescale. The monitoring of ion-channel activity occurs via measurement of the contrast in probe behavior between the on and off states of the ion channel. This protocol requires the dephasing due to ion-channel activity to be at least comparable to that due to the fluctuating background magnetic signal. We must therefore account for the decoherence due to the diffusion of water molecules, buffer molecules, saline components, as well as the transversal diffusion of lipid molecules in the cell membrane.

The nth nuclear spin with charge q_n, gyromagnetic ratio γ_n, velocity 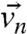, and spin vector 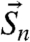interacts with the NV spin vector 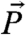and gyromagnetic ratio γ_p through the time-dependent dipole dominated interaction

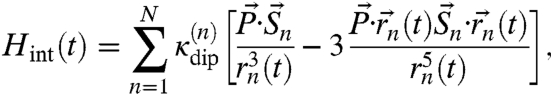[1]

where 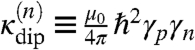are the probe-ion coupling strengths, and 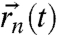is the time-dependent ion-probe separation. Additional Biot–Savart fields generated by the ion motion, both in the channel and the extracellular environment, are several orders of magnitude smaller than this dipole interaction and are neglected here. Any macroscopic fields due to intracellular ion currents are of nanotesla order and are effectively static over T₂ timescales. These effects will thus be suppressed by the spin-echo pulse sequence.

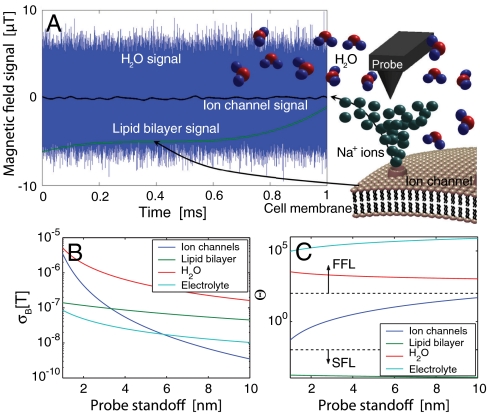
In Fig. 3A, we show typical field traces at a probe height of 1–10 nm above the ion channel, generated by the ambient environment and the onset of ion-flow as the channel opens. The contribution to the net field at the NV probe position from the various background diffusion processes dominate the ion-channel signal in terms of their amplitude. Critically, because the magnetometer mode detects the field by acquiring phase over the coherence time of the NV center, both the ion-channel signal and background are well below the nanotesla Hz^-1/2 sensitivity limit of the magnetometer over the (∼1 ns) self-correlated timescales of the environment. However, the effect of the various sources on the decoherence rate of the NV center are distinguishable because the amplitude-fluctuation frequency scales are very different, leading to remarkably different dephasing behavior.

Fig. 3.

Sources of magnetic field fluctuations and their relative amplitudes. (A) Calculated magnetic field signals from water, ion-channel, and lipid bilayer sources at a probe standoff of 4 nm over a 1 ms timescale. (B) Comparison of σ_B for various sources of magnetic fields. (C) Fluctuation regime, Θ = f_e/γ_pσ_B, for magnetic field sources vs. probe standoff. Rapidly fluctuating fields (Θ≫1) are said to be in the fast-fluctuating limit (FFL). Slowly fluctuating fields (Θ ≪ 1) are in the slow fluctuation limit (SFL). The ion-channel signal exists in the Θ ∼ 1 regime and therefore has an optimal dephasing effect on the NV probe.

To understand this effect, we need to consider the full quantum evolution of the NV probe. In the midst of this environment, the probe’s quantum state, described by the density matrix ρ(t), evolves according to the Liouville equation, 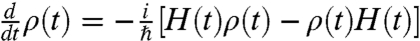, where ρ(t) is the incoherent thermal average over all possible unitary evolutions of the entire system, as described by the full Hamiltonian, H = H_nv + H_int + H_bg, where H_nv is the Hamiltonian of the NV system, and H_int describes the interaction of the NV system with the background environment (e.g., diffusion of ortho spin water species and ions in solution) and any intrinsic coupling to the local crystal environment. The self-evolution of the background system is described by H_bg, which, in the present methodology, is used to obtain the noise spectra of the various background processes. We note that the following analysis assumes dephasing to be the dominant decoherence channel in the system. We ignore relaxation processes because all magnetic fields considered are at least 4 orders of magnitude less than 2.88 GHz, and are hence unable to flip the probe spin over relevant timescales. Phonon excitation in the diamond crystal may also be neglected (17). Before moving onto the numerical simulations, we consider some important features of the problem.

The decoherence rate of the NV center is governed by the accumulated phase variance during the control cycle. Maximal dephasing due to a fluctuating field will occur at the cross-over point between the fast and slow fluctuation regimes (19). A measure of this point is the dimensionless ratio Θ ≡ f_e/γ_pσ_B, where τ_e = 1/f_e is the correlation time of the fluctuating signal, with cross-over at Θ ∼ 1.

In what follows, we consider exclusively the behavior of a sodium ion channel. Sodium-23 has an effective abundance of 100% and a nuclear magnetic moment of μ_Na = 2.22μ_N, where μ_N = 5.05 × 10^-27 JT^-1 is the nuclear magneton. Other magnetically active ion-channel species include potassium-39, having a 93.1% abundance and a nuclear magnetic moment of 0.391μ_N, and chlorine-35, having a 75.4% abundance and a nuclear magnetic moment of 0.821μ_N, ensuring sodium ions will interact most strongly with the NV center. We can estimate the field standard deviation 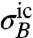due to the random nuclear spin of ions and bound water molecules moving through an ion channel (ic) as 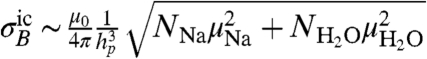, where N_Na and N_H2O are the average numbers of sodium ions and water molecules inside the channel. By modeling the channel as a cylinder with typical sodium channel influx/outflux rates (33), we may numerically calculate the rms fluctuation strength of the ion-channel magnetic field, 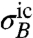, as a function of the probe standoff distance h_p, as shown in Fig. 3B. The fluctuation rate is defined by the rate at which ions move through the channel and is independent of whether the ions are moving into or out of the cell. However, in typical physiological processes (neuronal firing for example), the sodium flux will be inward. Ion flux rates give an effective fluctuation rate of 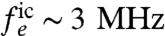(33). For probe-channel separations of 2–8 nm, values of Θ range from 0.4 to 40 (Fig. 3C). Thus, the ion-channel flow hovers near the cross-over point, with an induced dephasing rate of Γ_ic ∼ 10⁴–10⁵ Hz.

At these separation distances, the presence of the diamond surface is expected to have a negligible effect on the ion-channel dynamics. To reduce the decoherence effects of surface spins on the NV, the surface may be terminated with H or OH moieties. This surface termination essentially replaces the electron spins associated with the sp2 hybridized orbitals, with weaker nuclear spins (32). The ions in the channel, also being nuclear spins, couple very weakly to their surrounding environment. We may estimate their coupling to the diamond surface as 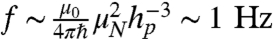, which is negligible compared to the fluctuation rate of the channel itself. Additionally, we may approximate the ratio between the magnetic force on the ions due to the surface spins and the electric force due to adjacent ions as 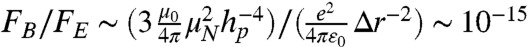, where Δr is the typical distance between adjacent ions in the channel. Similarly, the ratio between the magnetic force due to the NV spin and the electric force is 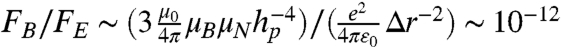, thus we expect the presence of the probe to be truly noninvasive.

We now consider the dephasing effects of the various sources of background magnetic fields. The first source of background noise is the fields arising from the motion of the water molecules and ions throughout the aqueous solution. Due to the nuclear spins of the hydrogen atoms, liquid water consists of a mixture of spin neutral (para) and spin-1 (ortho) molecules. The equilibrium ratio of ortho to para molecules (OP ratio) is 3∶1 (34), making 75% of water molecules magnetically active. In biological conditions, dissolved ions occur in concentrations 2–3 orders of magnitude below this number density and are ignored here (they are important however for calculations of the induced Stark shift; see below). The rms strength of the field due to the aqueous solution is 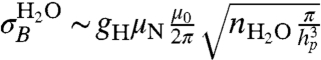. This magnetic field is therefore 1–2 orders of magnitude stronger than the field from the ion channel (Fig. 3 A and B). The fluctuation rate of the aqueous environment is dependent on the self-diffusion rate of the water molecules. Using D_H2O = 3 × 10^-9 m² s^-1, the fluctuation rate is 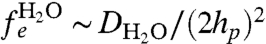. This fluctuation rate places the magnetic field due to the aqueous solution in the fast-fluctuation regime, with Θ_H2O ∼ 10³–10⁴ (Fig. 3B), giving a comparatively slow dephasing rate of 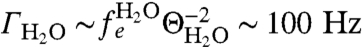and corresponding dephasing envelope .

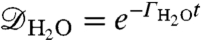An additional source of background dephasing is the lipid molecules comprising the cell membrane. Assuming magnetic contributions from hydrogen nuclei in the lipid molecules, lateral diffusion in the cell membrane gives rise to a fluctuating B field, with a characteristic frequency related to the diffusion rate. Atomic hydrogen densities in the membrane are n_H ∼ 3 × 10²⁸ m^-3. At room temperature, the populations of the spin states of hydrogen will be equal, thus the rms field strength is given by 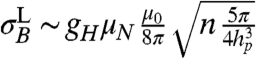. The strength of the fluctuating field due to the lipid bilayer is of the order of 10^-7 T (Fig. 3A). The diffusion constant for lateral Brownian motion of lipid molecules in lipid bilayers is D_L = 2 × 10^-15 m² s^-1 (35), giving a fluctuation frequency of 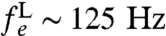and Θ_L ∼ 10^-4 (Fig. 3C). At this frequency, any quasi-static field effects will be predominantly suppressed by the spin-echo refocusing. The leading-order (gradient-channel) dephasing rate is given by (19) 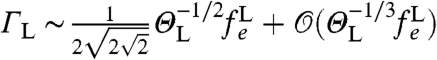, giving rise to dephasing rates of the order Γ_L ∼ 100 Hz, with corresponding dephasing envelope .

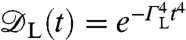The electric fields associated with the dissolved ions also interact with the NV center via the ground-state Stark effect. The coefficient for the frequency shift as a function of the electric field applied along the dominant (z) axis is given by R_3D = 3.5 × 10^-3 Hz m V^-1 (36). Fluctuations in the electric field may be related to an effective magnetic field via 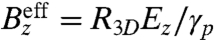, which may be used in an analysis similar to that above. An analysis using Debye–Hückel theory (37) shows charge fluctuations of an ionic solution in a spherical region Λ of radius R behave as 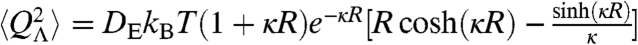, where D_E is the diffusion coefficient of the electrolyte, and κ is the inverse Debye length (l_D); l_D = 1/κ = 1.3 nm for biological conditions. Although this analysis applies to a region Λ embedded in an infinite bulk electrolyte system, simulation results discussed below show very good agreement when applied to the system considered here. The electric field variance may be obtained from 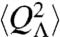, giving , as a function of h_p. Relaxation times for electric field fluctuations are 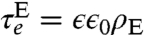(38), where ρ_E is the resistivity of the electrolyte, giving 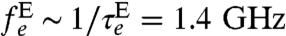under biological conditions. Given the relatively low strength (Fig. 3A) and short relaxation time of the effective Stark-induced magnetic field fluctuations (Θ ∼ 10⁵) (Fig. 3B), we expect the charge fluctuations associated with ions in solution to have little effect on the evolution of the probe.

Discussion

We now turn to the problem of noninvasively resolving the location of a sodium ion channel in a lipid bilayer membrane. When the channel is closed, the dephasing is the result of the background activity and is defined by 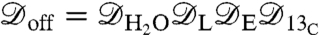. When the channel is open, the dephasing envelope is defined by 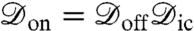. Maximum contrast will be achieved by optimizing the spin-echo interrogation time, τ, to ensure 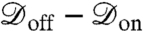is maximal. 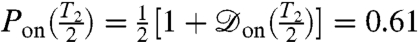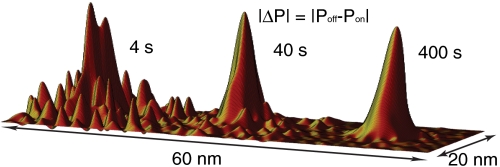Thus, in the vicinity of an open channel at the point of optimal contrast, τ ≈ T₂/2, we expect an ensemble ground-state population of , and 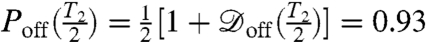otherwise. By scanning over an open ion channel and monitoring the probe via repeated measurements of the spin state, we may build up a population ensemble for each lateral point in the sample. The signal-to-noise ratio improves with the dwell time at each point. Fig. 4 shows simulated scans of a sodium ion channel with corresponding image acquisition times of 4, 40, and 400 s. It should be noted here that the spatial resolution available with this technique is beyond that achievable by magnetic field measurements alone, because for large Θ, .

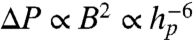Fig. 4.

Simulated spatial scans based on the ion channel as a dephasing source. Relative population differences are plotted for pixel dwell times of 10, 100 and 1,000 ms. Corresponding image acquisition times are 4, 40, and 400 s.

We may employ similar techniques to temporally resolve a sodium ion-channel switch-on event. By monitoring a single point, we may build up a measurement record, 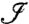. In an experimental situation, measurement frequency has an upper limit of f_m = (τ + τ_m + τ_2π)^-1, where τ_m ≈ 900 ns is the time required for photon collection, and τ_2π is the time required for all three microwave pulses. A tradeoff exists between the increased dephasing due to longer interrogation times and the corresponding reduction in measurement frequency. Interrogation times are limited by the intrinsic T₂ time of the crystal. A second tradeoff exists between the variance of a given set of N_τ consecutive measurements and the temporal resolution of the probe. For the monitoring of a switching event, the spin state may be inferred with increased confidence by performing a running average over a larger number of data points, N_τ. However, increasing N_τ will lead to a longer time lag before a definitive result is obtained. The uncertainty in the ion-channel state goes as 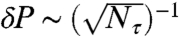, where N_τ is the number of points included in the dynamic averaging. We must take sufficient N_τ to ensure that δP < ΔP(τ,h_p,T₂) = P_off - P_on. The temporal resolution depends on the width of the dynamic average and is given by δt ∼ N_τ(τ + τ_m), giving the relationship 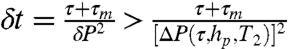. We wish to minimize this function with respect to τ for a given standoff (h_p) and T₂ time.

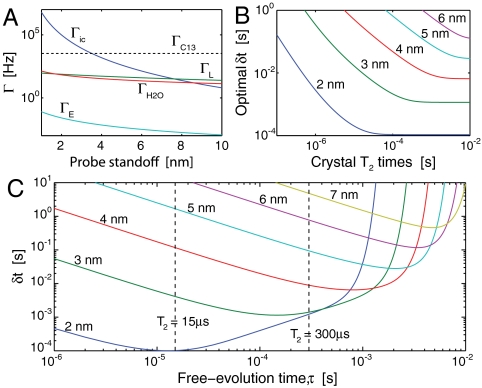
In reality, not all crystals are manufactured with equal T₂ times. An important question is therefore, for a given T₂, what is the best temporal resolution we may hope to achieve? Fig. 5B shows the optimal temporal resolution as a function of T₂. It can be seen that δt improves monotonically with T₂ until T₂ exceeds the dephasing time due the fluctuating background fields (Fig. 5A). Beyond this point, no advantage is found from extending T₂.

Fig. 5.

Temporal characteristics of the measurement protocol. (A) Dephasing rates due to the sources of magnetic field plotted as a function of probe standoff, h_p. (B) Optimum temporal resolution as a function of crystal T₂ times for h_p = 2–6 nm. (C) Temporal resolution as a function of interrogation time, τ, for separations of 2–7 nm. The limits corresponding to T₂ = 15 μs and T₂ = 300 μs are shown as vertical dashed lines.

A plot of δt as a function of τ is given in Fig. 5C for standoffs of 2–6 nm. Solid lines depict the resolution that maybe achieved with T₂ = 300 μs. Dashed lines represent the resolution that may be achieved by extending T₂ beyond the dephasing times of background fields. We see that δt diverges as τ → T₂ and is optimal for τ → 1/Γ_ic.

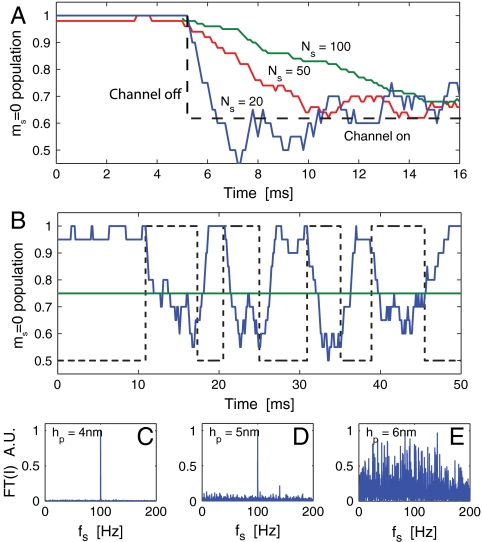
As an example of monitoring of ion-channel behavior, we consider a crystal with a T₂ time of 300 μs at a standoff of 3 nm. Fig. 5C tells us that an optimal temporal resolution of δt ∼ 1.1 ms may be achieved by choosing τ ∼ 100 μs. This interrogation time suggests an optimal running average will employ N_τ = δt(τ + τ_m)^-1 ≈ 11 data points. Fig. 6A shows a simulated detection of a sodium ion-channel switch-on event using N_τ = 20, 50, and 100 points. The effect of increasing N_τ is shown to give poorer temporal resolution but also produces a lower variance in the signal, which may be necessary if there is little contrast between P_off and P_on. Conversely, decreasing N_τ results in an improvement to the temporal resolution but leads to a larger signal variation.

Fig. 6.

Theoretical results for the detection of ion-channel operation. (A) Plot illustrating the dependence of temporal resolution (δt) and signal variance (δP) on the number of data points included in the running average (N_s). (B) Simulated reconstruction of a sodium ion-channel signal with a 200 Hz switching rate using optical readout of an NV center (blue curve). The actual ion-channel state (on/off) is depicted by the dashed line, and the green line depicts the analytic confidence threshold. Fourier transforms of measurement records are shown in C–E for standoffs of 4, 5, and 6 nm, respectively. Switching dynamics are clearly resolvable for h_p < 6 nm, beyond which there is little contrast between decoherence due to the ion-channel signal and the background.

We now consider an ion-channel switching between states after an average waiting time of 5 ms (200 Hz) (Fig. 6B). To ensure the condition δP < ΔP is satisfied, we perform the analysis using N_τ = 20, giving a resolution of δt ≈ 2 ms. The blue curve shows the response of the NV population to changes in the ion-channel state. Fourier transforms of the measurement record, , are shown in Fig. 6 C–E). The switching dynamics are clearly resolvable for heights less than 6 nm. The dominant spectral frequency is 100 Hz which is half the 200 Hz switching rate as expected. Beyond 6 nm, the contrast between P_off and P_on is too small to be resolvable due to the T₂ limited temporal resolution, as given in Fig. 5B. This contrast may be improved via the manufacturing of nanocrystals with improved T₂ times, allowing for longer interrogation times (dashed curves, Fig. 5C).

With regard to scaleup to a wide-field imaging capability, beyond the obvious extrinsic scaling of the number of single channel detection elements (in conjunction with microconfocal arrays), we consider an intrinsic scaleup strategy using many NV centers in a bulk diamond probe (39), with photons collected in a pixel arrangement. Because the activity of adjacent ion channels is correlated by the micrometer scale activity of the membrane, the fluorescence of adjacent NV centers will likewise be correlated, thus wide-field detection will occur via a fluorescence contrast across the pixel. Implementation of this scheme involves a random distribution of NV centers in a bulk diamond crystal. The highest reported NV density is 2.8 × 10²⁴ m^-3 (40), giving typical NV–NV couplings of < 10 MHz which are strong enough to introduce significant additional decoherence. We seek a compromise between increased population contrast and increased decoherence rates due to higher NV densities, n_nv, given by 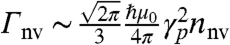(19).

For ion-channel operation correlated across each pixel, the total population contrast ΔΦ between off and on states is obtained by averaging the local NV state population change 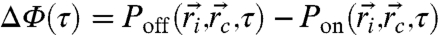over all NV positions 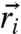and orientations, and ion-channel positions 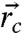and species, and maximizing with respect to τ. As an example, consider a crystal with n_nv = 10²⁴ m^-3 whose surface is brought within 3 nm of the cell membrane containing an sodium and potassium ion-channel densities of ∼2 × 10¹⁵ m^-2 (41). Higher densities will yield better results, however, these have not been realized experimentally as yet, and electron spins in residual nitrogen will begin to induce NV spin flips. We expect ion-channel activity to be correlated across pixel areas of 1 × 1 μm, so the population contrast between off and on states is ΔΦ ≈ 15. At these densities, the optimal interrogation time is τ ∼ 0.8 μs, yielding an improvement in the temporal resolution by a factor of 10,000, opening up the potential for single-shot measurements of ion-channel activity across each pixel.

We have carried out an extensive analysis of the quantum dynamics of a NV diamond probe in the cell-membrane environment and determined the theoretical sensitivity for the detection, monitoring, and imaging of single ion-channel function through quantum decoherence. Using current demonstrated technology, a temporal resolution in the 1–10 ms range is possible, with spatial resolution at the nanometer level. With the scope for scaleup and unique scanning modes, this fundamentally different detection mode has the potential to revolutionize the characterization of ion-channel action, and possibly other membrane proteins, with important implications for molecular biology and drug discovery.

Materials and Methods

Geometry.

All numerical calculations were performed with Monte Carlo methods using MATLAB, and conducted on a rectangular slab. Reflective boundary conditions are imposed at the top and bottom, representing the diamond crystal and lipid bilayer, respectively. Periodic boundary conditions are imposed on the sides of the volume. The lower boundary also hosts ion channels with the surface density given in the main text. The NV center is placed at a variable height above the diamond crystal boundary.

Ion Channel.

We assume the waiting time between ion ejections from the channel to follow a Poissonian distribution about a mean rate of 3 MHz. Each ion will couple to the NV spin via Eq. 1, with r_n(t) describing the spatial separation between the NV spin and the dipoles in the ion channel. Upon exiting the channel, the timescales associated with the ion motion will change to that described by the self-diffusion rate of nuclear spins in the electrolyte. Because the addition of ions to the electrolyte at these frequencies is slow compared to the characteristic Brownian motion of the electrolyte, any ions exiting the channel will rapidly diffuse away. Thus for simplicity, ions are terminated upon exiting the channel, making the nuclear dipole concentration near the channel opening equal to that of the bulk.

Magnetic Field of the Electrolyte.

For the purpose of modeling the fluctuating field due to self-diffusive behavior of the electrolyte, we do not distinguish between different species of nuclear dipole, and instead consider a weighted-average nuclear dipole moment as defined by the concentrations of water molecules and dissolved ions. The coupling of each ion to the NV center is again described by Eq. 1, however, couplings between ions, or to the mean field, are ignored because the associated timescales are much slower than those of their diffusive motion. Because of this weak coupling, each ion is assumed to not flip during its interaction with the NV center. Each of the r_n(t) then describes a random walk of a dipole of random but fixed orientation, as defined by the self-diffusion coefficient of the electrolyte.

Magnetic Field of the Lipid Bilayer.

Lipid diffusive motion is modeled in a similar fashion to the bulk nuclear motion using the diffusion rate given in the main text, however, the lipids are confined to the two-dimensional plane comprising the lower boundary of the system geometry.

Electric Field of the Electrolyte.

Regions of nonneutral charge density, together with their correlation lengths are found using Monte Carlo numerical techniques outlined in ref. 37. The rms electric field felt by the NV center may then be found by integrating over the charge distribution in the electrolyte.