TABLE 6.
Precision of predicted SEs for groups composed at random
| Error% |
||||||
|---|---|---|---|---|---|---|
| Scheme |  |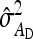
 |
 |
 |
 |
 |
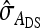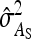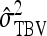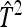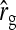| Basic | 2 | 0 | −1 | 1 | 5 | 1 |
| Alt. 1 | 1 | −11 | −3 | −2 | 3 | 146 |
| Alt. 2 | 3 | 3 | 1 | 1 | 2 | 129 |
| Alt. 3 | 4 | 0 | 0 | 2 | 9 | 121 |
| Alt. 4 | 0 | 8 | −1 | −1 | −1 | 47 |
| Alt. 5 | 3 | −6 | −1 | 0 | 7 | 134 |
| Alt. 6 | 1 | −4 | −1 | −2 | 1 | −5 |
| Alt. 7 | 2 | 7 | −1 | 0 | 1 | 85 |
| Alt. 8 | 3 | 1 | 0 | 2 | 6 | 2 |
| Alt. 9 | −1 | 2 | 2 | 3 | 5 | −2 |
| Alt. 10 | 2 | −1 | 0 | 3 | 5 | −10 |
| Alt. 11 | 2 | 0 | −3 | 0 | 2 | −7 |
| Alt. 12 | 2 | 1 | 0 | 1 | 7 | 2 |
| Alt. 13 | 2 | 0 | −1 | −1 | 2 | −1 |
| Alt. 14 | 2 | 2 | 0 | 2 | 7 | 0 |
| Alt. 15 | −2 | 1 | −1 | −2 | 3 | 0 |
| Alt. 16 | 2 | −3 | 4 | 2 | 5 | −6 |
| Alt. 17 | −1 | −1 | 4 | 2 | 5 | −10 |
| Alt. 18 | 3 | −4 | 1 | 0 | 3 | −5 |
| Alt. 19 | 1 | −1 | 4 | 4 | 6 | −38 |
| Alt. 20 | 0 | −6 | −1 | 1 | 2 | −33 |
See Table 5 for description of schemes. Error% = 100% × (predicted − empirical)/empirical. Empirical SEs were based on stochastic simulations with 1000 replicates. With 1000 replicates, the relative SE of the empirical SE equals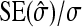 
≈ 
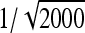≈ 0.022 (Stuart and Ord 1994). Therefore, when predictions equal the true values, E[error%] = 0, and the SE of error% given the predicted value equals ∼2.2%. Then the expected absolute error equals E[|error%|] ≈ 1.8%, and |error%| > 4.4% indicates significant bias (P < 0.05; two-sided, not accounting for multiple testing).