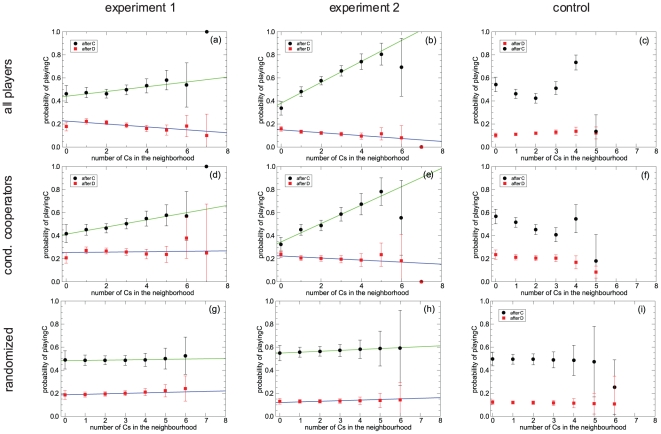
Figure 2. Context-dependent behavior depends also on the player's previous action or “mood”.
Probabilities of cooperating after playing C or D, conditioned to the context (number of cooperators in the previous round). Panels (a)–(c) show results for all players, whereas panels (d)–(f) show results for the group of players referred to as conditional cooperators. Panels (a) and (d) correspond to results of experiment 1, panels (b) and (e) to experiment 2, and panels (c) and (f) to the control experiment. The parameters of the linear fits can be found in Table 1. The plots demonstrate that there is a strong dependence on the context for players that cooperated in the previous round (i.e., were in a “cooperative mood”), the cooperation probability increasing rapidly as a function of the number of cooperative neighbors in a manner similar to the conditional cooperators found by Fischbacher et al. [19]. However, after having defected, players behave in a manner that shares features of exploiting behavior, cooperating with equal or less probability as the number of cooperators in their neighborhood increases. The very different behavior of players in the control experiment illustrates that conditional cooperation arises as a direct reciprocity effect —which is pointless if neighbors change every round. The conditioning of cooperation to the previous round is different in both experiments, which provides a strong indication that players learnt to play as the experiment proceeded, moody conditional cooperation being more clearly observed in the plots corresponding to experiment 2. Finally, panels (g)–(i) show the probabilities of cooperating after playing C or D, conditioned to the context (number of cooperators in the previous round), averaged over 1000 random shufflings of players in the lattice. Panel (g) corresponds to experiment 1, panel (h) to experiment 2, and panel (i) to the control experiment. The results show that there is no dependence on the context, proving that the dependence revealed in panels (a)–(f) is statistically significant.