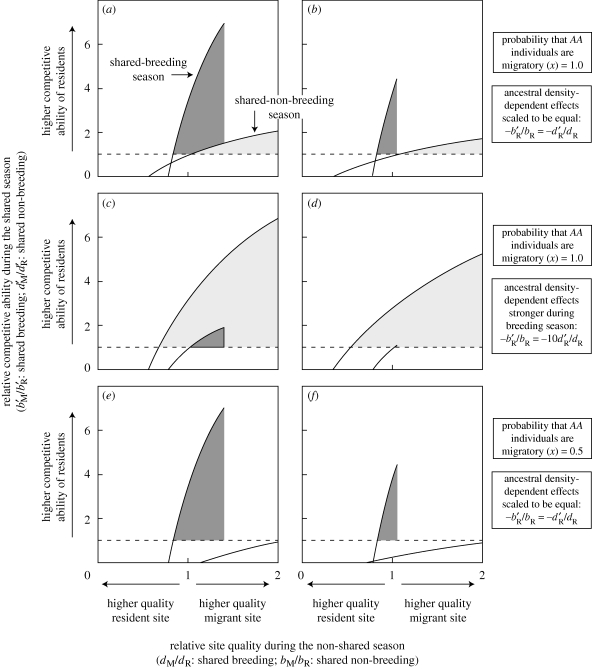
Figure 2.
Conditions under which a migratory allele is able to invade a resident population in relation to competition (y-axis) and relative site quality (x-axis). In the ancestor, scaled density-dependent effects on birth in the shared-breeding case and on survival in the shared-non-breeding case are equal for the (a) high-fecundity and low-survival (HF–LS) life history and for the (b) low-fecundity and high-survival (LF–HS) life history, respectively with x = 1.0 and h = 0.5. Parts (a,b) support the prediction from condition (3.4) that the migrant allele will invade more easily in the shared-breeding case for both life histories when density-dependent effects on birth and survival are scaled to be equal. In the ancestor, scaled density-dependent effects on birth in the shared-breeding case are 10 times greater than the scaled density-dependent effects on survival in the shared-non-breeding case for the (c) HF–LS life history and for the (d) LF–HS life history, respectively, with x = 1.0 and h = 0.5. Parts (c,d) support the prediction from condition (3.4) that the migrant allele can invade more easily in the shared-non-breeding case for both life histories when density-dependent effects on birth are stronger than effects on survival. In (e,f), the demographic parameters are the same as in (a,b), except the migration probability is lowered to x = 0.5. Parts (e,f) suggest that the invasion of the migratory allele is not affected strongly by x in the shared-breeding case, but is affected strongly in the shared-non-breeding case. In the shared-breeding scenario, the sharp threshold along the x-axis occurs because the probability of survival cannot be greater than 1.0. Thus, if the resident ancestors' survivorship is 0.7125, the maximum value of dM/dR is 1.4. For (a,c,e), dR = 0.7125 and bR = 1.0, and for (b,d,f), dR = 0.95 and bR = 0.5. For (a–f), 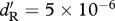 , for (a,e)
, for (a,e) 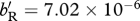 , for (b,f)
, for (b,f) 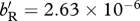 , whereas for (c)
, whereas for (c) 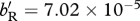 and for (d)
and for (d) 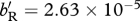 . All other parameter values are fixed across panels: Q = 1, m12 = 0.05, m21 = 0.05, sM = 0.95 and sD = 0.95.
. All other parameter values are fixed across panels: Q = 1, m12 = 0.05, m21 = 0.05, sM = 0.95 and sD = 0.95.