Preclinical evaluation of nuclear morphometry and tissue topology for breast carcinoma detection and margin assessment

Abstract

Prevention and early detection of breast cancer are the major prophylactic measures taken to reduce the breast cancer related mortality and morbidity. Clinical management of breast cancer largely relies on the efficacy of the breast-conserving surgeries and the subsequent radiation therapy. A key problem that limits the success of these surgeries is the lack of accurate, real-time knowledge about the positive tumor margins in the surgically excised tumors in the operating room. This leads to tumor recurrence and, hence, the need for repeated surgeries. Current intraoperative techniques such as frozen section pathology or touch imprint cytology severely suffer from poor sampling and non-optimal detection sensitivity. Even though histopathology analysis can provide information on positive tumor margins post-operatively (~2–3 days), this information is of no immediate utility in the operating rooms. In this article, we propose a novel image analysis method for tumor margin assessment based on nuclear morphometry and tissue topology and demonstrate its high sensitivity/specificity in preclinical animal model of breast carcinoma. The method relies on imaging nuclear-specific fluorescence in the excised surgical specimen and on extracting nuclear morphometric parameters (size, number, and area fraction) from the spatial distribution of the observed fluorescence in the tissue. We also report the utility of tissue topology in tumor margin assessment by measuring the fractal dimension in the same set of images. By a systematic analysis of multiple breast tissues specimens, we show here that the proposed method is not only accurate (~97% sensitivity and 96% specificity) in thin sections, but also in three-dimensional (3D) thick tissues that mimic the realistic lumpectomy specimens. Our data clearly precludes the utility of nuclear size as a reliable diagnostic criterion for tumor margin assessment. On the other hand, nuclear area fraction addresses this issue very effectively since it is a combination of both nuclear size and count in any given region of the analyzed image, and thus yields high sensitivity and specificity (~97%) in tumor detection. This is further substantiated by an independent parameter, fractal dimension, based on the tissue topology. Although the basic definition of cancer as an uncontrolled cell growth entails a high nuclear density in tumor regions, a simple but systematic exploration of nuclear distribution in thick tissues by nuclear morphometry and tissue topology as performed in this study has never been carried out, to the best of our knowledge. We discuss the practical aspects of implementing this imaging approach in automated tissue sampling scenario where the accuracy of tumor margin assessment can be significantly increased by scanning the entire surgical specimen rather than sampling only a few sections as in current histopathology analysis.

Introduction

Breast carcinoma is the most frequently diagnosed malignancy in women. Currently, a woman living in the U.S has a 12.3% lifetime risk of developing breast cancer. In the last two decades, the incidence rate of small (<2 cm) tumors has increased by ~2% per year suggesting the critical role of mammography and other screening strategies in detecting early cancers. Despite this good news, breast cancer continues to account for more than 21% of cancer-related deaths worldwide and for the estimated 40,000 breast cancer-related deaths in the U.S alone in 2010. A combination of breast-conservation surgery (lumpectomy) and radiation therapy has become a standard of treatment for most in situ and invasive cancers [1-9]. Removing all tumor present—with “clear margins”—is the goal of breast-conserving surgery. Failure to do so significantly increases the risk of local recurrence. While local recurrence may be treatable (mastectomy, chemotherapy ± radiation), it increases the risk of systemic recurrence and death. Margin assessment depends on histopathologic analysis of the lumpectomy specimen, which typically takes 2–3 days [10-14]. Information from this analysis is thus of no immediate value during surgery. Several other approaches (e.g., imprint cytology, tomography etc.,) have shown promise but none has yet made the jump from clinical research to clinical acceptance [10, 12, 15-17]. The use of intra-operative frozen section has the longest track record. Frozen section is not as reliable as permanent (H&E) section and specimens processed in this manner cannot be evaluated further. This emphasizes the value of developing technologies that can incrementally add to our ability to detect cancer intraoperatively, even if these technologies do not have outstanding sensitivity and/or specificity. It is evident that we need alternate detection technologies that can augment the existing repertoire of clinical diagnostic modalities. Our long-term goal is to develop optical imaging approaches for enabling the tumor margin detection in intraoperative settings [18-20]. In this study, by systematic comparison of normal and breast tumor tissues from preclinical animal models of breast carcinoma, we demonstrate that nuclear morphometric parameters (size and area fraction) and tissue topology parameter (fractal dimension) can be potentially used as reliable imaging tools for discriminating normal and breast tissues in vivo. In order to confirm the utility of this approach in human breast specimens, we carried out similar morphometric analysis in a human tissue microarray with four different cases of breast tumor status. Our results indicate that the nuclear morphometry has a systematic dependence on the tumor stage and/or aggressiveness. By extending the scope of the current observations to excised human tissues, it is possible to achieve rapid assessment of tumor margins in intraoperative clinical settings thereby alleviating the aforementioned problems in clinical management of breast cancer.

Materials and methods

Cell culture and tumor generation in rats

Adult female Fisher 344 rats (180–210 g body weight) were used in the current studies. MAT B-III rat breast cancer cell line was purchased from ATCC (Manassas, VA, USA) and cultured in McCoy’s 5a medium supplemented with 10% fetal bovine serum. When confluent, cells were harvested and washed twice with PBS, counted with trypan blue staining for viability. In order to generate breast tumor xenografts, the rats were anesthetized by maintaining a steady stream of oxygen/isoflurane using a nose cone/face mask. After removing the hair and sterilizing the skin, 10⁶ cell/0.2 ml were injected subcutaneously into the mammary fat pads under the rat’s nipple on the right breast. Left breasts without tumor cell injection served as normal control for every animal. All experiments were conducted on both left (normal) and right (tumor) breasts in each animal. Rats were observed at set intervals (days 0, 1, 3, 5, 7, 9, 11, 13, 15, and 21) for tumor growth. We observed that the above inoculation protocol generated tumors (100% efficiency) within 2 days, and the tumor size reached typically 2–4 cm in 3 weeks. All procedures used were carefully controlled to adhere to the approved animal protocols (Cedars-Sinai Medical Center, Institutional Animal Care and Use Committee).

Image acquisition

A wide-field fluorescence microscopy imaging system (Nikon TE2000; CoolSNAP CCD camera) was employed in collecting all the images reported in this study. This system utilizes the mercury arc lamp for excitation and appropriate filter cubes for collecting fluorescence from the specimen (DAPI filter: 360/40 nm excitation; 400 nm LP dichroic; 460/50 nm emission and Alexa 488 filter: 480/30 nm excitation; 505 nm LP dichroic; 535/40 nm emission). An automated stage-scanning feature of the imaging system enabled the rapid acquisition of data along both X and Y axes. After 3 weeks of tumor growth, animals were anesthetized and tumor tissues were excised and immediately stored in formalin containers. In order to obtain a matched pair of breast specimens without the tumor, mammary fat pads and the surrounding breast stroma were also collected from the left breast (no tumor injection) of each animal. For this study, 12 animals were subdivided into two groups: group 1 (n = 6)—animal tissues were used in making paraffin blocks and subsequent thin tissue sectioning (5–10 microns thickness) and group 2 (n = 6)—animal tissues were used as thick tissue specimens (~4 cm³ volume) for three-dimensional (3D) imaging as described in the next section. Our goal was to demonstrate the proposed method of nuclear morphometry analysis in thin tissue sections (group 1) as well as in realistic thick breast tissues that mimic the surgical specimens (group 2). Since the purpose of this study is to evaluate the rapid assessment of nuclear architecture in tissues, we chose to use a DNA intercalating fluorescent dye, DAPI (Invitrogen, Carlsbad, CA, USA) that has bright fluorescence for fast imaging of nuclear-specific fluorescence from the breast tissues. The DAPI-labeling protocol was optimized for good signal-to-noise ratio as well as for rapid readout of the images. We found that both the thin tissue slides and the thick tissue specimens could be labeled rapidly (~3 min, room temperature, 50 ng/ml working concentration) for optimal imaging. Supporting immunofluorescence studies were carried out by labeling the group 1 tissue sections with cancer-specific primary antibodies (rabbit polyclonal) raised against key metabolic targets Glucose transporter 1 (GLUT1), epidermal growth factor receptor (EGFR), fatty acid synthase (FAS), and Akt (Abcam, Cambridge, MA, USA). Fluorescence visualization of the tissue slides was enhanced by secondary antibodies conjugated with Alexa 488 fluorophore. Human tissue microarrays (US Biomax Inc, MD, USA) were labeled with DAPI and cell proliferation marker, Ki67 tagged with Alexa 488 fluorophore. Data acquisition was facilitated by the QED Invivo Software (Media Cybernetics Inc., Silverspring, MD, USA). Serial images along X, Y were obtained and tiled together to obtain the complete image of the entire specimen. Three-dimensional stacks of images were obtained by collecting series of XY images over a defined Z-depth range (~100–150 microns). Typical time of acquisition per image (1392 × 1040 pixels) was under 2 s.

Data analysis

It is worth mentioning that this study focuses on not developing new image analysis methods but in utilizing the currently available image analysis methods to address the vital clinical question of tumor margin detection. Our long-term goal is to extend the scope of this study to images obtained by any imaging system so that the method itself becomes independent of any specific imaging platform. Tissue fluorescence images obtained by the aforementioned protocols were analyzed for three morphometric parameters, namely, nuclear size, circularity, and nuclear count. The rationale behind choosing these parameters is the fact that tumors are most commonly associated with increased cell proliferation as compared with the non-neoplastic (normal) regions which, in turn, leads to a higher nuclear density as well. Furthermore, it is a common observation among the histopathologists that in tumor regions, there is an increased nuclear-to-cytoplasmic ratio as compared with the normal regions. In this article, we attempted to evaluate the feasibility of quantitative characterization of nuclear architecture (as exemplified by the three parameters described above) in breast tumors. Toward this direction, we applied a well-known algorithm, namely, Watershed Algorithm—for automatic estimation of nuclear size and count in the fluorescence images obtained. Watershed algorithm is one of the many methods of image segmentation, i.e., the process of partitioning a digital image into multiple segments (sets of pixels) [21-23]. The watershed transformation considers the gradient magnitude of an image as a topographic surface. Pixels having the highest gradient magnitude intensities correspond to watershed lines, which represent the region boundaries. Water placed on any pixel enclosed by a common watershed line flows downhill to a common local intensity minimum. Pixels draining to a common minimum form a catch basin, which represents a segment. In this case, this approach is expected to segment the nuclear fluorescence images and extract the statistics such as nuclear size and count. We used a custom-plugin written in the popular ImageJ (NIH) program for the watershed analysis of the images (http://rsbweb.nih.gov/ij/). We further tested another equivalent approach for achieving automated nuclear statistics based on the topology of the digital images by the CellAnalyst software program (http://www.assaysoft.com) [24-28]. In this approach, an image pixel is defined to have four vertices (corners), four edges, and one face. Algebraic topology uses algebraic operations with these objects to capture and count the number of completed cycles—circular sequences of edges. The completion of a cycle indicates the presence of a cell (or nuclei in our case). The topological nature of the algorithm makes it especially suitable for nuclear counting since (a) the count of nuclei is independent of their locations, (b) the measurements of nuclei are independent of their orientations with respect to the image grid, and (c) the nuclei and other features are captured with no deformation, smoothing, blurring, or approximation. In order to evaluate whether the difference in nuclear morphometry is significant enough to serve as a reliable diagnosis criterion in situations that mimic the intraoperative settings, we also computed the Nuclear Area Fraction in each image by using a particle analyzer plugin written in the ImageJ software (http://rsbweb.nih.gov/ij/). This parameter yields a comprehensive picture of nuclear distribution which takes into account both the nuclear size/shape and the nuclear count. Finally, in order to measure the complexity in the tissue images, we also measured an important topological parameter, “fractal dimension” which measures the degree of connectedness. Fractal is typically a rough and geometric shape that looks almost identical at arbitrarily various levels of magnification. This feature stems from the principle of self-similarity and is a defining characteristic of the spatial complexity. For the present purpose of understanding complex, highly connected nuclear architecture in the fluorescence images of the breast tissues, it is possible to quantify the tissue complexity by measuring the fractal dimension [29-32]. Fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. We chose to measure the fractal dimension to investigate whether this parameter can be a robust indicator of the breast tumor tissue complexity and if this parameter can also serve as a reliable diagnostic criterion for margin assessment. This was measured by box-counting algorithm written and available in the ImageJ software.

Statistical analysis

Morphological and topological data set from normal and tumor specimens from both Group I and Group II were analyzed for statistical significance by performing Students’ t-test (unpaired set with equal variance). In each group, specimens from at least five different animals were included to address the issue of variations from animal-to-animal. The data presented here had a p value, p < 0.0001.

Results

The basic premise of nuclear morphometry analysis is demonstrated in Fig. 1 which shows the essential steps involved in extracting the required information (nuclear size/shape, count etc.,) from the raw fluorescence image. A breast tissue is inherently heterogenous since it is composed of multiple cell types (epithelial, fibroblasts, endothelial, and fatty tissue components), and the resulting nuclear architecture can be fairly complex. It is, therefore, imperative to validate the proposed nuclear morphometry analysis to confirm the variability in analysis and the statistical significance of the extracted parameters. Figure 1a shows a representative 2D image of fluorescent microbeads of different sizes and shapes. Image processing (binary threshold) and image segmentation steps as demonstrated in Fig. 1b–d yield the required nuclear parameters. We next tested whether the proposed nuclear morphometric parameters can reliably discriminate tumor margins in breast tissue specimens. In order to do this, we first chose thin sections of tissue specimens that were known to contain tumor regions bordering with normal epithelium. Watershed and Edge detection analysis were carried out on this set of specimens as follows: individual images of 915 × 686 μm size were subdivided into regular image units of 50 × 686 μm size. Nuclear morphometric parameters were calculated on these individual image units. A representative data set and the associated analyses are presented in Fig. 2: nuclear size and count systematically decrease as one moves from tumor-rich regions to normal-only regions, as graphically illustrated. Normal breast regions tend to have smaller nuclear size and lesser nuclear count as compared to the tumor-filled breast regions. In contrast to the above two parameters, nuclear circularity does not exhibit a significant difference between normal and tumor regions. In light of this observation, we chose not to include nuclear circularity in the later analysis of breast tissue morphometry. The increase in nuclear density in tumor-rich regions of the tissue poses another technical challenge in the analysis of nuclear morphometry. In some regions, as can be seen in Fig. 2a, the overlap of the neighboring nuclei is high enough to introduce artifacts in nuclear counting since this may exceed the best optical resolution that can be achieved (~0.20 μm). This potentially underestimates the resulting nuclear count. Although this is an inherent limitation of optical imaging methods, one can also derive another useful topological parameter from this situation: In tissue images with high degree of overlap between individual nuclei (or cells in general), a topological survey can be performed by measuring the degree of connectedness or nonlinearity in the images. By measuring the fractal dimension of these images (as described in the “Materials and Methods” section), one can infer the extent of complexity in the images. We computed the fractal dimension in the individual image subunits as described above. Figure 2e demonstrates that the computed fractal dimension changes from 1.6 (tumor) to 1.2 (normal) mimicking the spatial profile of the nuclear morphometry (size and count) parameters. This feature was observed in all the images analyzed. Having shown that nuclear morphometry and tissue topology analysis can yield a robust measure of the spatial transition from normal to tumor regions in breast tissue sections, we then analyzed multiple sets of images from normal and tumor tissue sections obtained from different animals with varying stages of tumor growth. A rigorous statistical analysis of all the morphometric and topological parameters was carried out. For clarity, a representative statistical analysis of nuclear size is given in Fig. 3a. As can be seen, the mean nuclear size was found to be statistically different between normal and tumor tissue sections.

Fig. 1.

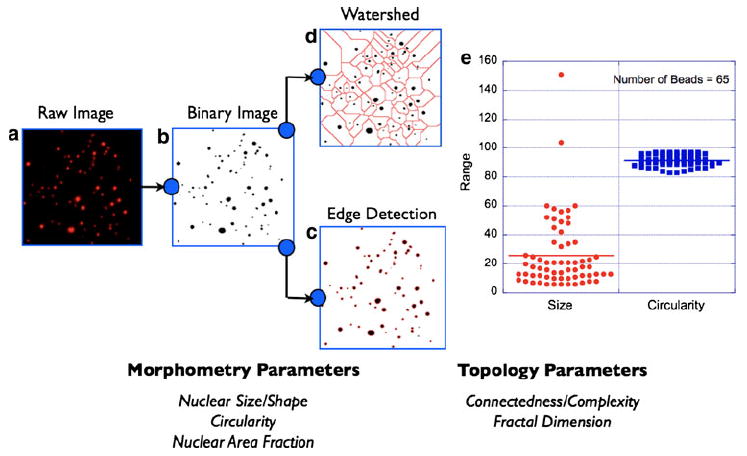
Nuclear morphometry/topology analysis schematic. A 2D image of fluorescent microbeads of various sizes is shown (a). This situation mimics the nuclear distribution in a typical tissue labeled with the intercalating dye, DAPI. Image segmentation process begins with intensity thresholding of the raw image (b). This step addresses the heterogeneity in fluorescence intensity across the field-of-view. The next step is to render the thresholded binary image to detailed morphometric analysis by either of the two methods: edge detection (c) or watershed algorithm (d). Morphometric parameters of relevance to this study are (i) nuclear size, (ii) nuclear circularity, and (iii) nuclear area fraction as defined in the text and exemplified in (e). In complex images where the nuclear area fraction is high, the above two image segmentation approaches can yield an underestimate of the calculated nuclear volume fractions. This situation occurs when the overlap of neighboring nuclei (e.g., tumor regions) exceeds the optical resolution of the imaging system (~0.25 μm). In order to address this inherent limitation, the processed images are also analyzed for topological information such as connectedness and fractal dimension. See main text for more details. Together, morphometric and topological analyses of the tissue fluorescence images provide a comprehensive picture of the tissue architecture

Fig. 2.

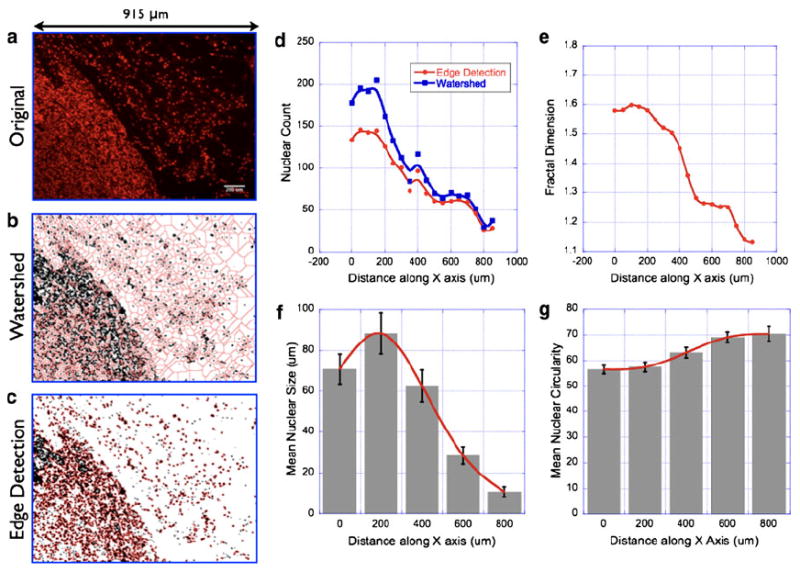
Nuclear morphometry/topology analysis in thin sections of breast tumor tissues. Representative nuclear fluorescence image of a tumor tissue section with a bordering normal epithelium (a) (Scale bar = 200 μm). The nuclear area fraction is significantly higher in the tumor region as compared with that of the normal epithelium. In order to quantify these differences, morphometric parameters were analyzed in multiple tissue sections and presented here. See main text for discussion on statistical analysis. Image segmentation by watershed algorithm (b) and edge-detection algorithm (c) yielded two different models for quantifying the nuclear distribution in the images. The original image (915 μm × 684 μm) was divided into regular subunits of size (20 μm × 684 μm). Mean nuclear count in each image subunit by the two aforementioned algorithms as shown in (d). Although both the algorithms yielded similar spatial profile of nuclear distribution in the tissue images, the edge-detection approach was found to be more accurate in delineating the individual nuclei in a cluster whose size was beyond the resolution of the optical imaging system. Fractal dimension was also computed in these image subunits as described in the main text and presented in (e). Mean nuclear size and circularity are shown in (f) and (g)

Fig. 3.

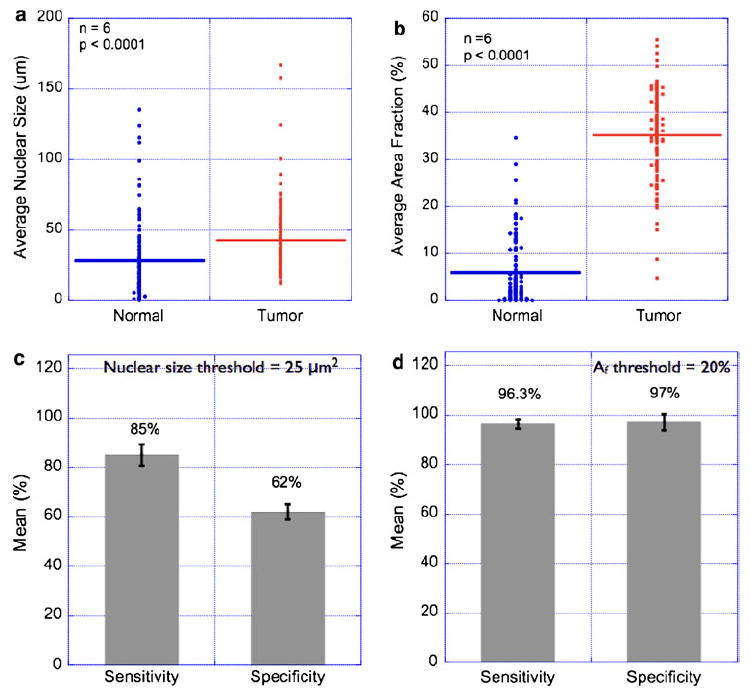
Statistical analysis of nuclear morphometry parameters in breast tissues. Nuclear morphometry parameters were calculated in multiple images of normal and breast-tumor specimens as described in the “Material and methods” section. Each image (462 μm × 346 μm size) was divided into sub-images of size (50 μm × 50 μm), and the mean nuclear size was computed. This step ensured that the entire image was sampled with uniform sampling interval. Thus, every data point in the Fig. 3a, b represents mean nuclear size in the predefined sub-image regions. Statistical data from six representative pairs of normal and tumor regions are presented in (a). As can be seen, the observed difference in mean nuclear size in the normal and tumor regions was found to be statistically significant. However, the estimated sensitivity and specificity values from these data were only 85 and 62%, respectively (c). In order to remedy this problem, we measured the nuclear area fraction (A_f) which parameterizes a combination of nuclear size and number in a given region-of-interest. Statistical comparison of measured area fractions is shown in (b), and the corresponding sensitivity/specificity comparison is shown in (d). These results suggest that it is possible to achieve high sensitivity and high specificity in tumor diagnosis based on nuclear area fractions. It is worth mentioning that the nuclear size criterion can be made highly specific at the cost of decreasing sensitivity

In a typical lumpectomy procedure, the surgeon is guided by preoperative radiological images of the tumor for locating the tumor in the patient’s breast and for removing the tumor and the surrounding normal tissue. The immediate question is how much of this excised tissue is clear of tumor cells in the periphery. It is useful to have a specific diagnosis criterion that could potentially enable the surgeon in answering the above question. Based on our statistical results from Figs. 2 and 3a, we investigated whether the nuclear size could be such a diagnosis criterion. We tested this by the analyzing the tissue sections (n = 6) that contained both normal and tumor regions in the same field of view, as exemplified in Fig. 2a. By using a diagnosis criterion based on the nuclear size threshold of 25 μm² (as obtained from Fig. 3a), we computed the sensitivity and specificity in detecting tumor regions within a normal breast tissue (Table 1). In a binary classification scenario where the goal is to detect tumor regions (true positive) in an otherwise normal tissue periphery (true negative), sensitivity is the statistical measure of the proportion of true positives that are correctly identified and specificity is the corresponding statistical measure of the proportion of the true negatives that are correctly identified. This analysis is summarized in Fig. 3c where the sensitivity and specificity of detecting tumor regions were 85 and 62.5%, respectively. Although the difference in nuclear size was found to be statistically significant, we believe this may not be a good diagnosis criterion for implementing in an intraoperative setting. However, during the course of studies, we found that nuclear area fraction (which is a combination of nuclear size and count) provided not only a statistically significant difference between normal and tumor regions (Fig. 3b) but also yielded a very high sensitivity and specificity in the analysis of specimens with both normal and tumor regions (Fig. 3d). We believe this can be a simple, reliable, and reproducible diagnosis criterion that can be implemented in tumor margin detection in excised tumor tissues. In order to test this in more realistic (thick) breast tissues, we performed morphometric and topology analysis in Group II specimens as mentioned above. Figure 4a shows the schematic of 3D data acquisition. Representative montages of large field of view of normal and tumor breast tissues show that the nuclear count is significantly higher in the tumor tissue as compared with the normal counterpart. Computation of nuclear area fraction and fractal dimension in multiple specimens demonstrate the feasibility of applying this proposed morphometric/topological approach even thick excised tissues.

Table 1.

Sensitivity and Specificity calculations based on two diagnosis criteria

Diagnosis criterion	Nuclear size Threshold = 25 μm2	Nuclear area fraction Threshold = 20%
True positive (Tumor identified as tumor)	138/330 (41.1%)	49/82 (59.8%)
False positive (Normal identified as tumor)	16/330 (4.8%)	1/82 (1.2%)
True negative (Normal identified as normal)	92/330 (27.8%)	30/82 (36.5%)
False negative (Tumor identified as normal)	84/330 (25.5%)	2/82 (2.4%)
Sensitivity = [True positives/(true positives + false negatives)]	85.0 ± 2.5%	96.3 ± 1.5%
Specificity = [True negatives/(true negatives + false positives)]	62.5 ± 2.5%	97.0 ± 2.0%

Fig. 4.

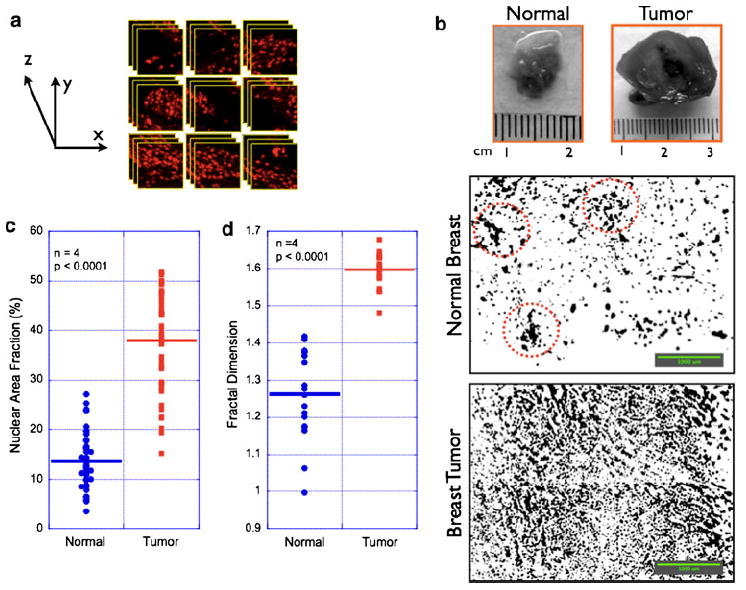
Three-dimensional nuclear imaging in excised breast tissues ex vivo. In contrast to the thin tissue sections, actual surgical specimens are three-dimensional, turbid tissues. a Schematic for obtaining 3D (x, y, z) image stacks from excised breast tissues. Image stacks were obtained from each field of view (465 × 425 μm) for user-defined z-depths (100 μm). This process is repeated at every field of view by translating the imaging stage systematically along the X and Y axes. b Representative montages of normal and tumor breast tissues (presented as a z-projection image from 20 images in each field of view; Scale bars = 1000 μm). c, d give the statistically significant differences in nuclear area fraction and fractal dimension between normal and tumor regions. This statistical significance was computed from the analysis of multiple images from different animals (n = 4 rats). As can be seen, both nuclear morphometry (area fraction) and tissue topology (fractal dimension) reliably discriminate the tumor regions from the normal tissue components obtained from the same animal. The apparently higher values of area fraction in normal tissue arise possibly from the other tissue components (ducts and fibrofatty components) in the normal breast of the animal that were stained with DAPI. These regions (marked in red circles) typically contribute to false negative values and can be reliably addressed by increasing the threshold (or cut-off) of the area fraction/fractal dimension parameters in the data acquisition/analysis system

Finally we extended the scope of our preclinical observations to human breast tumor cases where we asked the question if the proposed nuclear morphometry analysis can give insight into the various tumor stages and/or aggressiveness. Figure 5 shows representative nuclear fluorescence images on a tissue microarray (US Biomax Inc., #T085) labeled with cell proliferation marker (Ki67) and nuclear marker (DAPI). As can be seen from Fig. 5b nuclear count systematically increases in proportion to the aggressiveness of the breast cancer. As it is evident from the images, the nuclear grade (heterogeneity in nuclear size and shape) is also significantly different in breast carcinoma as compared with normal breast tissues thereby offering additional quantitative measures for rapid diagnosis in intra-operative settings.

Fig. 5.

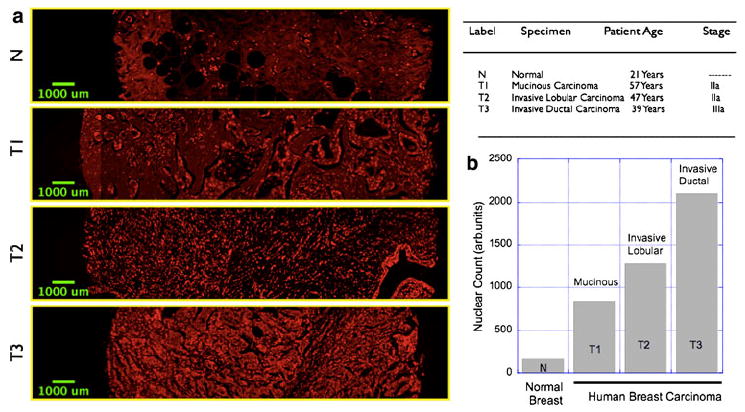
Nuclear morphometry imaging in human tissue microarray. a Representative images showing the nuclear distribution in normal, human breast (fibrofatty) tissue as well as in three breast carcinoma specimens with varying degrees of aggressiveness. The details of the specimens are given in the accompanying table. b Nuclear count and hence the nuclear area fraction increases progressively in accordance with the aggressiveness

Discussion

We demonstrated here the utility of measuring nuclear morphometric and tissue topology parameters in discriminating normal and tumor tissues in a rat model of breast carcinoma. The rationale behind this study is based on the well-known, drastic increase in cell proliferation that accompanies tumorigenesis. It is important to note that our major emphasis in this study was not on developing any new imaging technology for tumor margin assessment but on providing a novel and robust image analysis concept that can be employed in a practically platform-independent manner. In earlier studies and even in current practice of tumor histopathology, it is a commonplace observation that nuclear-to-cytoplasmic ratio increases in specimens obtained from breast tumors. However, while translating this observation to tissue specimens with both normal and tumor regions (as judged by immunofluorescence studies, data not shown), we arrived at the conclusion that nuclear size as a diagnostic criterion cannot yield good enough sensitivity and specificity in reliably delineating tumor regions in an otherwise normal breast tissue. Our data clearly precludes the utility of nuclear size as a reliable diagnostic criterion for tumor margin assessment. On the other hand, nuclear area fraction addresses this issue very effectively since it is a combination of both nuclear size and count in any given region of the analyzed image, and thus yields high sensitivity and specificity (~97%) in tumor detection. This is further substantiated by an independent parameter, fractal dimension, based on the tissue topology.

In this study, our goal was to report a proof-of-concept demonstration of the clinical utility of rapid assessment of nuclear morphometry and tissue topology and to propose a plausible intraoperative tumor margin detection avenue. Our results also point to the fact that the proposed diagnostic criterion is applicable not only in thin tissue sections but also in realistic thick excised tissues. The CFI Plan Fluor DLL 20X (Nikon; 0.50 numerical aperture; 2.10 mm working distance) objective lens used in this study allowed us to reproducibly obtain fluorescence signals up to 1.60 mm of the thick tissue sections. This reduction in “effective” working distance (as compared to the expected 2.10 mm for the objective lens) can be attributed to tissue absorption, shorter excitation wavelengths (~350 nm), as well as multiple scattering events in the tissue sections. Although this limits deeper penetration, it is important to note that the measurable tissue depth (~1.60 mm) is more than the typical depth (~1 mm) where the positive tumor margin is typically defined. We are currently exploring a multi-zoom macroscope (Nikon AZ100) and a low magnification objective lens (Nikon; AZ-Plan Fluor 5X/0.50 Numerical Aperture/15 mm working distance) for its increase in field of view as well as the speed. Finally, our data on human tissue microarrays further suggest that it is also possible to extend the scope of the proposed diagnostic criterion from tumor margin detection to preliminary tumor staging in operating rooms. The proposed method can rapidly give a spatial map of nuclear distribution in the excised tissue from which one can obtain information on potential “tumor-like” regions on the surface of the surgical specimen. In order to increase the precision in margin assessment, it is possible to label these “tumor-like” regions with cancer-specific antibodies tagged with fluorophores—without compromising the intraoperative diagnosis features (such as speed, sensitivity, and specificity) of the nuclear architecture imaging. It is equally important to conceive appropriate specimen handling strategies while extending the scope of this study in intraoperative settings to avoid commonly encountered problems such as specimen shrinkage and related artifacts [33, 34]. Recent studies have pointed out that the intraoperative touch imprint cytology methods do have significant limitations in terms of sensitivity in diagnosis as well as limited sampling issues [10, 12, 15, 35]. We envision that the strategy that is proposed in this manuscript can overcome these limitations since it is possible to obtain images by scanning the entire surgical specimen with an overall high sensitivity/specificity in diagnosis as illustrated in Fig. 4. Although the basic definition of cancer as an uncontrolled cell growth entails a high nuclear density in tumor regions, a simple but systematic exploration of nuclear distribution in thick tissues by nuclear morphometry and tissue topology as performed in this study has never been carried out, to the best of our knowledge. A logical next step of this study will be to test this idea in a clinical feasibility trial where the proposed method will be implemented to reliably identify tumor margins in excised lumpectomy/mastectomy specimens in breast-conserving surgeries.