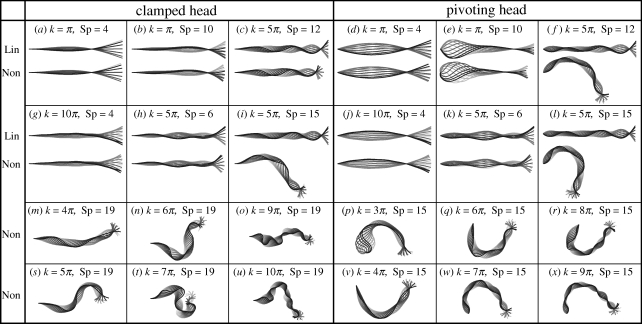
Figure 3.

Snapshots of the flagellar evolution for the clamped and pivoting head boundary conditions, plotted at equal time intervals (darker curves for later times). The internal sliding force is given by equation (2.3) for π ≤ k ≤ 10π and 4 ≤ Sp ≤ 19, as indicated, and the dimensionless force magnitude A is chosen to produce a maximum flagellum amplitude of 0.1L in equation (2.4) (electronic supplementary material, figure S1). (a–l) Comparison of the time evolution for the linear (Lin) and nonlinear (Non) theory. Note that the linear theory fails to predict the flagellar shape for cases (c,i,f,l), and that the pivoting boundary condition is more sensitive to the influence of the nonlinear dynamics. (m–x) Typical symmetry-breaking shapes, characterized by an ‘S’ for clamped boundary conditions (Sp = 19) and a ‘C’ for pivoting boundary conditions (Sp = 15). Furthermore, all beating patterns are periodic in time, despite their appearance.