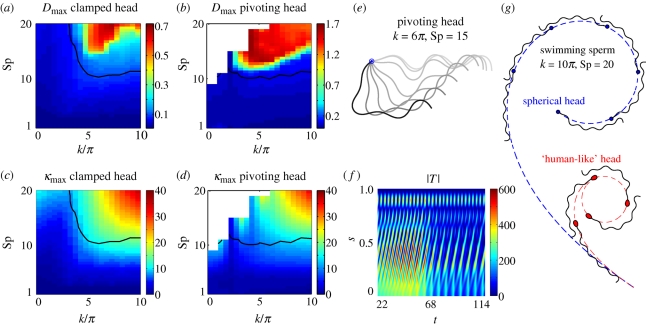
Figure 4.
The breakdown of linear theory, the symmetry-breaking instability and its consequences for the free head swimmer. (a,b) The discrepancy measure, Dmax = maxt,s|XN − XL|, is illustrated for varying internal shear wavenumber k, and sperm compliance parameter, Sp, in both the pivoting head and clamped head cases. (c,d), the maximum of the linear theory prediction of curvature, κmax, is presented. In all these four plots, the solid black contour marks where Dmax = 0.1, noting that significantly larger values are observed to characterize poor agreement between the linear and nonlinear theories. (e,f) The transient features of the symmetry-breaking bifurcation to asymmetric waveforms for the pivoting head boundary condition, when k = 6π and Sp = 15 (figure 3q). (e) Time sequence once the flagellar buckling instability can be readily observed, with waveforms overlaid at equal time intervals with the point of attachment in blue. The initial waveform (t = 18.18) is illustrated in light grey and the final waveform (t = 150.76) in black, with a progression in darkness with time. (f) The associated absolute tension |T| as a function of time t and arclength s. (g) The influence of the symmetry-breaking instability on the overall trajectory and flagellar beating pattern of the free swimming cell, plotted at equal time intervals. Smoothed trajectories are plotted for two different sperm head geometries: a spherical head (dashed blue) and a ‘human-like’ head morphology (dashed red), both with the same human-like head volume (Smith et al. 2009a). Here, the internal shear density is given by equation (2.3) with k = 10π and Sp = 20, and the dimensionless force magnitude A is 75% of the force amplitude used for the pivoting case when the maximum displacement is 0.1L (equation (2.4) and electronic supplementary material, figure S1). The buckling transition induces an asymmetric waveform that drives swimmers towards permanent circular paths; the swimming direction is inverted if f → −f in equation (2.1).