Further Insight and Additional Inference Methods for Polynomial Regression Applied to the Analysis of Congruence

Abstract

In their seminal paper, Edwards and Parry (1993) presented the polynomial regression as a better alternative to applying difference score in the study of congruence. While this method is increasingly applied in congruence research, its complexity relative to other methods for assessing congruence (e.g., difference score methods) was one of the main claims against its use. The objective of this work is to gain additional insight into the use of polynomial regression in the area of social and behavioral sciences. First, we elaborate on the meaning and the inference based on the coefficients obtained by applying polynomial regression and explain the mathematical terms that are used to describe response surfaces. Then, we introduce additional inference methods and illustrate their application on a real life example from the area of supportive exchanges, using data collected by the Smithers Institute at Cornell University (supported by the National Institute on Alcohol Abuse and Alcoholism). Our work is aimed to provide a guide to researchers who apply polynomial regression in order to assess the effect of congruence between two constructs and enable better understanding and interpretation of the results obtained.

Introduction

In recent years polynomial regression is increasingly used by social and behavioral scientists aiming to assess congruence between two constructs and its relationships with various outcomes. For example, in their study on multiple sources of feedback, Bailey and Fletcher (2002) used polynomial regression in order to explore changes in congruence between self and coworkers’ rating. Myers (2004) applied polynomial regression to study the influence of the congruence between pricing and venture strategies on venture performance. Jansen and Kristof-Brown (2005) incorporated the polynomial regression model within hierarchical linear modeling (HLM), examining the way by which the congruence between individual and work group hardiness impact employees’ satisfaction, psychological strain, and helping behavior. However, there is still an ongoing debate as to whether polynomial regression is indeed the appropriate model for analyzing congruence between two constructs. Edwards and Parry (1993) presented the polynomial regression as a better alternative to applying difference score in the study of congruence and they elaborated on the way by which this method can be used. Polynomial regression generalizes the difference score model. In difference scores analysis, the assumption is that the relationship between the two constructs and the outcome is only a function of the difference between the constructs, regardless of the constructs level. The model of polynomial regression is not based on this assumption and hence may capture more realistic and more complex relationships.

One of the main claims against using polynomial regression in congruence research is that its complexity relative to other methods for assessing congruence (e.g., those based on difference scores) may lead to interpretation and inference difficulties and to misconceptions (Tisak and Smith, 1994a; 1994b). Mathematical terms such as stationary point and principal axes, that are used to describe response surfaces based on polynomial regression, are often unfamiliar to social scientists. Consequently, the meaning of this method may not be fully captured and the translation of its associated mathematical concepts to social research context may be incorrect. Although Edwards (2001) addressed this critique (as well as other critiques raised against polynomial regression) in his paper on difference score myths, review of selected organizational papers using polynomial regression reveals that there is still room for further elaboration as to how to infer based on this method. One of the purposes of the current manuscript is to gain better insight as to the use of polynomial regression in the behavioral and social sciences, by providing additional explanations to those presented by Edwards and Parry (1993). We also introduce new inference methods based on polynomial regression, and illustrate how they help to understand, interpret and present the conclusions drawn by applying this regression model.

The paper is laid out as follows. Section 2 describes in much detail the methodological concepts behind polynomial regression. It includes an explanation on the parameters in polynomial regression, their meaning and the importance of some of their functions. Section 3 introduces an example from the area of supportive exchanges, where polynomial regression is applied in order to examine the extent to which congruence and incongruence between support received from (X₁) and support given to (X₂) the close social network of an employee predicts employee self esteem. In this section, we use data from a sample of blue collar workers, collected by the Smithers Institute at Cornell University (supported by the National Institute on Alcohol Abuse and Alcoholism, PI's: Samuel Bacharach and Peter Bamberger). In Section 4 we introduce additional inference methods (including graphical displays) for understanding and presenting the results obtained by polynomial regression. The inference methods presented in section 4 are illustrated by using the example described in section 3.

The Polynomial Regression Model

In general, polynomial regression of a predictor X on a dependent variable Y refers to a regression model which includes higher powers of X, beyond its linear term. Quadratic regression is a particular case of a polynomial regression, where two is the largest power of X. In the context of congruence analysis, polynomial regression is a quadratic regression model. Let X₁, X₂ denote the two constructs whose congruence is considered as a predictor of an outcome Y. The quadratic regression model, which expresses Y as a function of X₁ and X₂, includes linear as well as squared terms of each of these variables, and also their cross product. Thus, the regression equation is:

$$\begin{array}{cc}\hfill & Y=b_0+b_1{X}_1+b_2{X}_2+b_{11}{X}_1^2+b_{22}{X}_2^2+b_{12}{X}_1{X}_2+e\hfill \\ \hfill & =f(X_1,X_2)+e,\hfill \end{array}$$ (1)

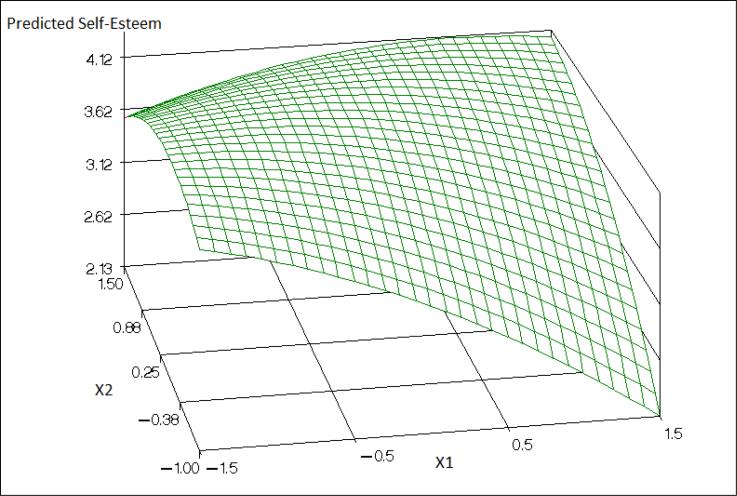
where the error term e is assumed to have an expected value of zero, and var(e) = σ². According to (1), E(Y) which denotes the conditional expectation of Y given X₁, X₂ is a surface in a three dimensional space, whose plane has the coordinates (X₁, X₂), and E(Y) = f(X₁, X₂), is the height of the surface for each point in this plane. Edwards and Parry (1993) used several examples to illustrate graphically how the shape of the response surface expressed by (1) depends on the regression coefficients. Figure 1 displays an example of a fitted response surface for data, where employee self-esteem (Y) was explained by the amount of support received from (X₁) and given to (X₂) the close social network of an employee.

Figure 1.

Fitted Surface Relating Self-Esteem to Support Received and Support Given.

Any response surface in the three dimensional space, can be moved up or down along the axis of E(Y), which is perpendicular to the plane (X₁, X₂). The location along this axis is characterized by the intercept (b₀). In order to facilitate the interpretation of the analyses results, we assume that X₁, X₂ were measured on the same scale, and both were centered at the midpoint of this scale. Thus, b₀ expresses the expected value of the response Y at the point where X₁ and X₂ obtain the mid-scale value. The coefficients b₁₁, b₂₂, and b₁₂ express the second order effects of X₁ and X₂. The derivative of E(Y) with respect to X₁ expresses the relative change in the expected value of Y, namely the slope of E(Y), when the change in the plane (X₁, X₂) is in the direction of X₁. This derivative, which equals

$$\frac{\partial E\left(Y\right)}{\partial X_1}=b_1+2b_{11}{X}_1+b_{12}{X}_2,$$ (2)

depends on both the value of X₁ and of X₂. It is equal to the coefficient b₁ only at the point (X₁, X₂) = (0, 0). Thus, in the particular case, when the explanatory variables (X₁, X₂) are expressed as deviations from their mid points, b₁ expresses the relative change in the expected value of Y, at the point where the two explanatory variables are equal to their mid points, where one moves in the direction of X₁. Similarly, b₂ is equal to the derivative

$$b_2={\phantom{[}\frac{\partial E\left(Y\right)}{\partial X_2}]}_{X_1=X_2=0}.$$

The vector defined as the gradient of the function expressed in (2) is:

$$\left(\frac{\partial E\left(Y\right)}{\partial X_1},\frac{\partial E\left(Y\right)}{\partial X_2}\right)=(b_1+2b_{11}{X}_1+b_{12}{X}_2,b_2+2b_{22}{X}_2+b_{12}{X}_1),$$ (3)

The first term of this vector is the expected relative change in Y, when moving in the direction of X₁, and the second is the expected relative change in E(Y), when moving in the direction of X₂.

Points that are of special interest are those where the difference between the two constructs equals zero (X₁ = X₂). These points form the so called “fit line” (or the line of congruence between X₁ and X₂) in the plane (X₁, X₂). Of similar interest, are the points on the (X₁, X₂) plane which form the so called “misfit” line (or the line of incongruence between X₁ and X₂). These are the points where X₁ = -X₂ (X₁ equals minus X₂). One of the main questions raised in congruence analysis, is with regard to the value of the slope (relative change) in the response E(Y), when moving in the plane (X₁, X₂) along the line of fit (where X₁=X₂). The answer in mathematical terms is the directional derivative of E(Y) with respect to the vector which satisfies the equality X₁ = X₂. All the points on the vector which satisfy this equality are of the type (X, X). This directional derivative which equals:

$$\frac{1}{\sqrt{2}}\{(b_1+b_2)+2(b_{11}+b_{22}+b_{12})X\},$$ (4)

presents the slope of the response, for each value X of a perfect match. Note that it depends on the specific matched value X. While both (b₁ + b₂)and (b₁₁ + b₂₂ + b₁₂)X are components of the slope (the directional derivative), we will refer to (b₁ + b₂) as the fixed component of the slope and to the coefficients of X, that is (b₁₁ + b₂₂ + b₁₂), as the slope's curvature.

Edwards and Parry (1993) used a different approach, without referring to the concept of gradient, in order to express the relative change of the response along the lines of fit and misfit. For the fit line, they substituted X = X₁ = X₂ in equation (1), to obtain the relationship between X and E(Y) on that line. The resulting expression is a second degree polynomial in X, where the slope is (b₁ + b₂) and the curvature is (b₁₁ + b₂₂ + b₁₂):

$$Y=b_0+(b_1+b_2)X+(b_{11}+b_{22}+b_{12})X^2+e.$$ (5)

This expression explains why the terms “slope” and “curvature” along the line of fit are used respectively for (b₁ + b₂) and (b₁₁ + b₂₂ + b₁₂) (e.g. Jansen and Kristof-Brown 2005). The derivative of Y with respect to X, which is obtained from (6), expresses the relative expected change in Y along the fit line, measured in the units of the fit line.

$$\frac{dE\left(Y\right)}{dX}=(b_1+b_2)+2(b_{11}+b_{22}+b_{12})X$$ (6)

Equations (6) differ from (4) by a factor of $\sqrt{2}$, because in (6), X is measured on the scale of the fit line, while in (4) it is measured on the scale of (X₁, X₂). A change of Δ in each of the original variables (X = X₁ = X₂) results in a change of $\sqrt{2}\Delta$ on the fit line. In this sense, moving one unit size step along (X₁, X₂) means taking a $\sqrt{2}$ size step along the line of fit. The difference in the expressions (4), (6) is of no practical significance, since the question of interest is whether either (b₁ + b₂) and/or (b₁₁ + b₂₂ + b₁₂) are equal to zero.

There are four possible conditions depending on whether the fixed component of the slope (b₁ + b₂), and/or the slope's curvature (b₁₁ + b₂₂ + b₁₂) are equal to zero. (1) When both are null, it means that the response is constant along the line of fit (where X₁ = X₂). (2) When only the curvature along the line is zero (b₁₁ + b₂₂ + b₁₂ = 0), the relative change of the response along the fit line does not depend on the matched value, and is constant along the fit line. (3) When the fixed component of the slope(b₁ + b₂) equals zero, the relative change of the response from X = 0 in the direction where X₁ and X₂ increase simultaneously, is zero. In other words, unless b₁₁ + b₂₂ + b₁₂ + 0 , we can only conclude from the value of (b₁ + b₂) about the relative change at the specific value X = 0. It is only in the particular case when the sum of the three second order coefficients is zero, that the directional derivative does not depend on X, and the relative change is the same for each matched value. (4) When both components are not null, the response is not constant from the point X = 0 in the direction where X₁ and X₂ increase simultaneously. In other words, the relative change (slope) from the point X = 0 in the direction where X increases, is not zero. However, one cannot conclude about the relative change in the response along the line of fit based on the value of (b₁ + b₂) alone, because (b₁₁ + b₂₂ + b₁₂) is not zero, meaning that the relative change (slope) of the response changes along the line of fit, depending on the matched value of X₁ and X₂.

The same question concerning the slope is of interest with regard to the “misfit” line, which is where the components have the same absolute value but are of opposite signs. The analogous expression to the derivative (6) is equal to:

$$(b_1-b_2)+2(b_{11}+b_{22}-b_{12})X.$$

The following section presents additional explanations concerning the shape of the response.

The second degree polynomial:

$$f(X_1,X_2)=b_0+b_1{X}_1+b_2{X}_2+b_{11}{X}_1^2+b_{22}{X}_2^2+b_{12}{X}_1{X}_2,$$ (7)

can be re-expressed in the following way:

$$f(X_1,X_2)=b_0^{\ast }+\left(X_1-X_1^{\ast },X_2-X_2^{\ast }\right)\left(\begin{array}{cc}\hfill b_{11}\hfill & \hfill b_{12}∕2\hfill \\ \hfill b_{12}∕2\hfill & \hfill b_{22}\hfill \end{array}\right)\left(\begin{array}{c}\hfill X_1-X_1^{\ast }\hfill \\ \hfill X_2-X_2^{\ast }\hfill \end{array}\right),$$ (8)

where $(X_1^{\ast },X_2^{\ast })$ is some arbitrarily selected point in the (X₁, X₂) plane, and

$$\begin{array}{cc}\hfill & b_0=b_0^{\ast }+b_{11}{\left(X_1^{\ast }\right)}^2+b_{22}{\left(X_2^{\ast }\right)}^2+b_{12}\left(X_1^{\ast }{X}_2^{\ast }\right)\hfill \\ \hfill & b_1=-2b_{11}{X}_1^{\ast }-b_{12}{X}_2^{\ast }{b}_2=-2b_{22}{X}_2^{\ast }-b_{12}{X}_1^{\ast }\hfill \end{array}$$ (9)

The second order coefficients b₁₁,b₂₂,b₁₂ are shape parameters, and are “location” parameters. Note that in both (7) and (8) the function f(X₁, X₂) is expressed as a function of 6 parameters, that are b₀,b₁,b₂ b₁₁,b₂₂,b₁₂ in (7), and $b_0^{\ast },b_{11},b_{22},b_{12},X_1^{\ast },X_2^{\ast }$ in (8).

In many cases, which we shall later specify, there is a certain point, called the stationary point, denoted here as (X₁₀, X₂₀), where the response has either a unique maximum, or a unique minimum, or a saddle point. In those cases, it is more meaningful to choose (X₁₀, X₂₀), which is a certain “center of gravity”, as $(X_1^{\ast },X_2^{\ast })$ in presentation (8). If we move the rigid surface which f(X₁, X₂) forms in the three dimensional space parallel to the (X₁, X₂) plane in various directions without changing its form (no stretching to either direction), it will alter the value of the stationary point.

The shape in terms of the curvature of the response is determined by the matrix of the quadratic form, denoted by B.

$$B=\left(\begin{array}{cc}\hfill b_{11}\hfill & \hfill b_{12}∕2\hfill \\ \hfill b_{12}∕2\hfill & \hfill b_{22}\hfill \end{array}\right).$$ (10)

Its off diagonal element expresses the curvature shared by the two variables. In most cases, B will be non singular, and the stationary point will then be uniquely defined. Its coordinates can be derived by equating to zero the two equations obtained by differentiating f(X₁, X₂) with respect to X₁ and to X₂ (which is the same as finding the point where the gradient vector equals zero). Thus, according to (3), in order to find the coordinates of the stationary point, we solve the 2 equations:

$$\begin{array}{cc}\hfill \frac{\partial E\left(Y\right)}{\partial X_1}& =b_1+2b_{11}{X}_{10}+b_{12}{X}_{20}=0\hfill \\ \hfill \frac{\partial E\left(Y\right)}{\partial X_2}& =b_2+2b_{22}{X}_{20}+b_{12}{X}_{10}=0\hfill \end{array}$$ (11)

Whether the surface has a maximum or minimum, or has a saddle at the stationary point, is determined by the matrix of the second derivatives, known as the Hessian of f(X₁, X₂).

$$Hessian=\left(\begin{array}{cc}\hfill \frac{{\partial }^{2}f(X_1,X_2)}{\partial X_1^2}\hfill & \hfill \frac{{\partial }^{2}f(X_1,X_2)}{\partial X_1\partial X_2}\hfill \\ \hfill \frac{{\partial }^{2}f(X_1,X_2)}{\partial X_1\partial X_2}\hfill & \hfill \frac{{\partial }^{2}f(X_1,X_2)}{\partial X_2^2}\hfill \end{array}\right).$$

When the Hessian is negative/positive definite the surface has a maximum/minimum respectively, and it has a saddle point when the Hessian is singular.

In the particular case when:

$$f(X_1,X_2)=a+b(X_1^2+X_2^2-2X_1{X}_2)=a+b{(X_1-X_2)}^2$$ (12)

the matrix B has the particular form:

$$B=\left(\begin{array}{cc}\hfill b\hfill & \hfill b\hfill \\ \hfill b\hfill & \hfill b\hfill \end{array}\right).$$ (13)

In that case, all the points on the fit line satisfy the set of equations (11) and the response has its largest or smallest value depending on the sign of b, for every value of the two predictors as long as they are equal.

So far, we elaborated on the meaning and importance of two points in the plane (X₁, X₂), that is the stationary point (X₁₀, X₂₀) and the point of origin (0, 0). In the following, we discuss the meaning and relevance of the two principal axes which are two lines that lie in the (X₁, X₂) plane. The property of interest that characterizes the principal axes, relates to the curvature of the response. When the surface is convex, it has a minimum, and the upward curvature is largest along the first principal axis and least along the second. Conversely, for concave surfaces, it has a maximum, and the downward curvature is smallest along the first principal axis and largest along the second.

The original variables (X₁, X₂) whose response is given in (8), can be transformed to two new variables (X_P1, X_P2) that are linear combinations of (X₁, X₂), such that the matrix B of their response function has zeroes as its off diagonal elements. This transformation involves the same mathematical procedure as the one required to perform principal component analysis, where a rotation is applied to obtain new uncorrelated variables. The transformation from (X₁, X₂) to (X_P1, X_P2) is done by diagonalizing the matrix $B=\left(\begin{array}{cc}\hfill b_{11}\hfill & \hfill b_{12}∕2\hfill \\ \hfill b_{12}∕2\hfill & \hfill b_{22}\hfill \end{array}\right)$. For easier interpretation, the transformation can be performed on the shifter variables $(X_1^{\ast },X_2^{\ast })=(X_1\text{-}{X}_{10},X_2\text{-}{X}_{20})$, so that the stationary point, if uniquely determined, will be in the origin. The representation of the response in the new coordinate system is then:

$$f(X_{P1}^{\ast },X_{P2}^{\ast })=b_0^{\ast }+\left(X_{P1}^{\ast },X_{P2}^{\ast }\right)\left(\begin{array}{cc}\hfill {\lambda }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\lambda }_2\hfill \end{array}\right)\left(\begin{array}{c}\hfill X_{P1}^{\ast }\hfill \\ \hfill X_{P2}^{\ast }\hfill \end{array}\right)=b_0^{\ast }+{\lambda }_1{\left(X_{P1}^{\ast }\right)}^2+{\lambda }_2{\left(X_{P2}^{\ast }\right)}^2,$$ (14)

where λ₁,λ₂ are the two eigenvalues of B. This presentation is also called the canonical model. After the transformation, the coordinate system has the two principal axes as its two orthogonal axes. The sum of the eigenvalues (λ₁ + λ₂) is equal to (b₁₁ + b₂₂) , which is the sum of the diagonal elements of B. In the analysis of principal components, where the diagonalization is performed on the variance/covariance matrix, each eigenvalue contributes to the total sum of variances. In congruence analysis, each of the two eigenvalues has a contribution to the curvature of the response surface.

When one of the eigenvalues of B equals zero, then by definition its corresponding eigenvector u satisfies the equation Bu = 0 and therefore, u^T Bu = 0 (the quadratic form of the response at (u₁, u₂) equals zero). It means that the response function for all the points (X₁, X₂) in the direction of u is actually a linear function. Similarly, for the points that form a line parallel to the direction of u, the response is a linear function of the constructs.

In the next section we present a real life example on which the main concepts presented above are illustrated.

Example: The Effect of Supportive Exchange Patterns on Employee Self-Esteem

Literature in the area of supportive relations suggests that receiving social support is a phenomenon embedded in the broader context of an individual's supportive exchange relationships (e.g., Buunk, Doosje, Liesbet, & Hopstaken, 1993). Accordingly, researchers suggested that the effect of receiving social support on well-being may depend upon whether the amount of support received from others is perceived by an individual as being equal to (i.e., the exchange of support is perceived as reciprocal); greater (i.e., the exchange of support is perceived as over-reciprocating) or lower (i.e., the exchange of support is perceived as under-reciprocating) than the amount of support he/she perceive to give to others (Rook, 1987).

Research in this area often draws on two different explanatory frameworks. The first is based on Equity Theory (Walster, Walster, & Berscheid, 1978), suggesting an advantage to reciprocal exchanges over under-reciprocating or over-reciprocating supportive exchanges in promoting positive self-image and social satisfaction resulting from compliance with reciprocity norms (Gouldner, 1960). Based on this perspective, any violation of reciprocity norms (i.e., under- and over-reciprocating supportive exchanges) is expected to generate negative feelings and emotions and may be harmful to the self-image of an individual (Rook, 1987).

The other perspective is based on the Theory of Esteem Enhancement (Batson, 1998), suggesting an advantage to under-reciprocating supportive exchanges over reciprocal and over-reciprocating supportive exchanges in promoting positive self-image grounded on a sense of being an important and valuable person. This perspective also suggests that over-reciprocating exchanges may lead to a state of dependency and incompetence which may be deleterious for the self-perception of the recipient (Väänänen, Buunk, Kivimaki, Pentti, & Vahtera, 2005).

While support was found for both perspectives, research in this area to date has mainly focused on exploring the general differences between the three patterns of supportive exchanges (i.e., reciprocal, over- and under-reciprocating), without considering the variance in the amount of support received and given in the relationships. For example, researchers (e.g., Buunk et al., 1993) examined the extent to which relationships perceived as reciprocal, under-reciprocating or over-reciprocating differ in their impact on individuals’ social satisfaction, self-image and general well-being. The measurements typically used in these studies ask participants to select the pattern of supportive exchange that best describe their relationships, without indicating the amount of support received and given in such relationships. Other studies included measurements of the amount of support received and given, but applied these in ways (e.g., using the difference score between support received and given and in some cases dividing the results between three categories representing reciprocal, under- or over-reciprocating exchanges) that limited the inference based on the complex interplay between giving and receiving support (e.g., Fukada and Jou, 2002).

Accordingly, we suggest that better understanding of the effect of supportive exchanges can be gained by testing a framework that captures the degree of incongruence (or difference) between giving and receiving support, as well as how much support is received and given in the supportive exchange (i.e., the level of support received and given). Such an approach would allow for example, distinguishing between reciprocal exchanges of high quality (i.e., high levels of support received and given) and those of low quality (i.e., low levels of support received and given). It would also allow to capture the extent of under-reciprocation (i.e., the extent to which support given exceeds that received) and over-reciprocation (i.e., the extent to which support received exceeds that given), and explore their effect on individuals’ well-being. In this sense, the current example (inspired by Nahum-Shani, Bamberger & Bacharach, 2010) explores the effect of supportive exchange patterns on employee self-esteem. We use this framework to test two competing hypotheses based on the two perspectives noted above. Based on the equity-based perspective, we hypothesize the following:

Hypothesis 1a: Employee self-esteem reduces to the extent that there is incongruence between the amount of support received from and the amount of support given to the close social network of an employee (i.e., to the extent that the difference between receiving and giving support increases, such that the exchange of support becomes more over- or under-reciprocating).

Hypothesis 1b: When there is congruence between the amount of support an employee receives and gives to his/her close social network (i.e., the exchange of support is reciprocal), employee self-esteem increases to the extent that the amount (i.e., the level) of support received or given increases (i.e., the quality of the reciprocal supportive exchange increases).

Based on esteem-enhancement theory, we hypothesize the following:

Hypothesis 2a: Employee self-esteem increases to the extent that support given to the close social network of an employee exceeds support received (i.e., greater incongruence, such that the exchange of support becomes more under-reciprocating).

Hypothesis 2b: Employee self-esteem reduces to the extent that support received exceeds support given (i.e., greater incongruence, such that the exchange of support becomes more over-reciprocating).

We used data (n=1004) drawn from a dataset collected by the Smithers Institute at Cornell University in the context of a grant from the National Institute of Alcohol Abuse and Alcoholism. The sample included blue collar workers employed in three sectors in the United States: Transportation, Manufacturing and Construction.

The measurements used in this example were as follows: Support perceived to be received from (X₁) and given to (X₂) the close social network of an employee were measured on the basis of Caplan, Cobb, French, Van Harrison & Pinneau (1975) instrument. Subjects were asked to identify those people with whom they have close relationships, and for each one of them to report the extent of instrumental support received from (using 2 items, ranging from 1: “not at all” to 4: “a great deal”; Cronbach alpha=0.73) and given to (using 2 corresponding items, ranging from 1: “not at all” to 4: “a great deal”; Cronbach alpha=0.83) him/her. The constructs of support received (X₁) and given to (X₂) were obtained by aggregating the relevant items across those close relationships identified by an employee. The dependent variable, employee Self-Esteem was measured one year (+/- two weeks) after the measurement of support received and given, using Rosenberg's (1965) global self-esteem scale, which includes ten items ranging from 1: “strongly disagree” to 5: strongly agree; (Cronbach alpha=0.82).

In order to test our hypotheses, the amount of support received and the amount of support given were scale centered (centered at the mid-point of their scale) and polynomial regression method was applied. According to Edwards and Parry (1993), and Aiken and West (1991), such centering facilitates the interpretation of the coefficients on X₁ and X₂ , which then represent the slope of the surface at the center of the (X₁, X₂) plane, where the origin of the X₁ and X₂ is located.

Table 1 presents the means, standard deviations, minimum and maximum of employee self esteem and the scale centered support received and support given. Table 2 presents the results of the polynomial regression analysis (this table also includes the first order model because often researchers are interested in assessing the extent to which the second order components add to the variance explained by the first-order components), and Figure 1 is the plot of the corresponding estimated response surface.

Table 1.

Simple Statistics of the Variables of Interest

Variable	Mean	Std Dev	Min	Max
Self Esteem	4.07	0.37	2.40	5.00
Support received (X1)	0.84	0.55	-1.50	1.50
Support given (X2)	1.34	0.31	-1.00	1.50

Table 2.

Estimated Coefficients of the Regression Model

	First Order Model		Polynomial Model
Effect	Estimate	SE	Estimate	SE
Intercept	3.99***	0.05	3.92***	0.07
X1	-0.02	0.02	-0.29**	0.11
X2	0.07	0.04	0.43**	0.17
X12			-0.11**	0.04
X22			-0.24**	0.09
X1*X2			0.30***	0.10
R-square	.002		0.02

While the first order model (Table 2) is not significant, by adding the second order components we obtain a model that significantly predicts self esteem. Based on the coefficients in Table 2, the stationary point and the principal axes were derived. The stationary point, which was found to be (-0.47, 0.61), is within the range of the component measures. At this point, the amount of support received is lower than that given, and according to the estimated model, the response has its maximum. The first principal axis with a corresponding eigenvalue λ₁= -0.006 was X₂= 0.92+0.66X₁. The second principal axis was X₂=-0.11-1.52X₁ with the corresponding eigenvalue λ₂= -0.337 (Formulas showing how to derive the equations of the principal axes from the estimated regression coefficients can be found in Edwards and Parry, 1993). Note that the first eigenvalue is small in its absolute value, which indicates that the matrix B is close to being singular. Consequently, as explained in the previous section, along lines parallel to the first principal axis X₂=0.92+0.66X₁, the response (self esteem) has the shape of a linear function.

Table 3 presents the hypothesis test results regarding the slope and curvature along the lines of fit and misfit. This table includes two sections, the first focuses on testing the composite hypothesis that both the slope and curvatures along each of the two lines (fit and misfit lines) equal zero (corresponding to using F statistics in regression analysis to test the global hypothesis that the set of all regression coefficients equals zero). The second part examines whether the slope, or curvature, or both significantly differ from zero (this section is relevant when the composite hypothesis is rejected, and corresponds to testing whether each individual regression coefficient equals zero).

Table 3.

Inference on the Slope and Curvature along the Fit and Misfit Lines.

Hypotheses:	Num DF	Den DF	F Value	Pr > F
Fit Line
b1+b2=0, b11+b12+b22=0	2	998	1.45	0.24
Misfit Line
b1-b2=0, b11-b22+b12=0	2	998	5.56	0.01

Hypotheses:	Estimate	SE	DF	t Value	Pr > |t|
Misfit line
b11-b12+b22=0	-0.65	0.15	998	-3.33	0.001
b1-b2=0	-0.72	0.25	998	-2.83	0.01
Fit Line
b11+b22+b12=0	-0.04	0.06	998	-0.64	0.53
b1+b2=0	0.15	0.12	998	1.19	0.23

According to Table 3, we cannot reject the null hypothesis that both the slope along the line of fit (b₁ + b₂) and the curvature along that line (b₁₁ + b₂₂ + b₁₂) are equal to zero. This means that the predicted value of employee self esteem is constant along the line of fit (where support received equals that given) regardless of the matched value of the amount of support received or given. These results are inconsistent with Hypothesis 1b, which suggests that under conditions of congruence between support received and support given (i.e., the exchange of support is reciprocal), employee self-esteem increases to the extent that the level of support received or given increases.

Concerning the line of misfit (X₁ = -X₂), the results presented in Table 3 indicate that both the slope at the point of fit [(b₁ – b₂) =-0.72, p=0.01], and the curvature [(b₁₁ + b₂₂ – b₁₂)=-0.65, p<0.001] along the line of misfit significantly differ from zero. More specifically, consider the point (0, 0) where both the support received (X₁) and given (X₂) equal 2.5 (their mid-point). This point lies on the intersection of the fit and misfit lines. Since (b₁ – b₂) is significantly negative, it indicates that the expected relative change in employee self esteem reduces from the point (0, 0), in the direction where the support received increases while support given reduces. The significant curvature indicates that the slope (the expected relative change in employee self esteem) is getting more and more negative as we go along the line of misfit in the direction where support received increases while support given reduces. To illustrate this, consider moving along the line of misfit from the origin to the point (1, -1), and then to the point (2, -2). At the point (0, 0) the slope is: $\frac{1}{\sqrt{2}}\{({\mathrm{b}}_1-{\mathrm{b}}_2)+2({\mathrm{b}}_{11}+{\mathrm{b}}_{22}-{\mathrm{b}}_{12})\mathrm{X}\}=\frac{1}{\sqrt{2}}(-0.29-0.44)=-0.516$. At the point (1, -1) the slope is: $\frac{1}{\sqrt{2}}\{(-0.29-0.44)+2(-0.11-0.24-0.30)1\}=-0.156-0.92=-1.44$, which is lower by 0.92 relative to the slope at the point (0,0). Similarly, at the point (2, -2) the slope is: $\frac{1}{\sqrt{2}}\{(-0.29-0.44)+2(-0.11-0.30-0.24)2\}=-0.156-1.84=-2.36$, which is again lower 2 by 0.92 relative to the slope at the point (1, -1). The change in the slope when moving one unit along the line of misfit, in the direction where X₁ increases and X₂ reduces is: $\sqrt{2}(-0.11-0.30-0.24)=\sqrt{2}(-0.65)=-0.92$.

These results support hypothesis 2b, indicating that employee self-esteem reduces to the extent that support received exceeds support given (i.e., to the extent that there is greater incongruence in the form of over-reciprocation). Still, the results obtained so far do not fully address hypothesis 1a, which suggests that self-esteem reduces to the extent that there is incongruence between support received and given, as well as hypothesis 2a, which suggest that self-esteem increases to the extent that support given exceeds support received.

Accordingly, in the following section, we present additional inference methods that improve our ability to draw useful conclusions from the estimated polynomial model.

Inference Based on the Polynomial Regression Model

Contour Plots

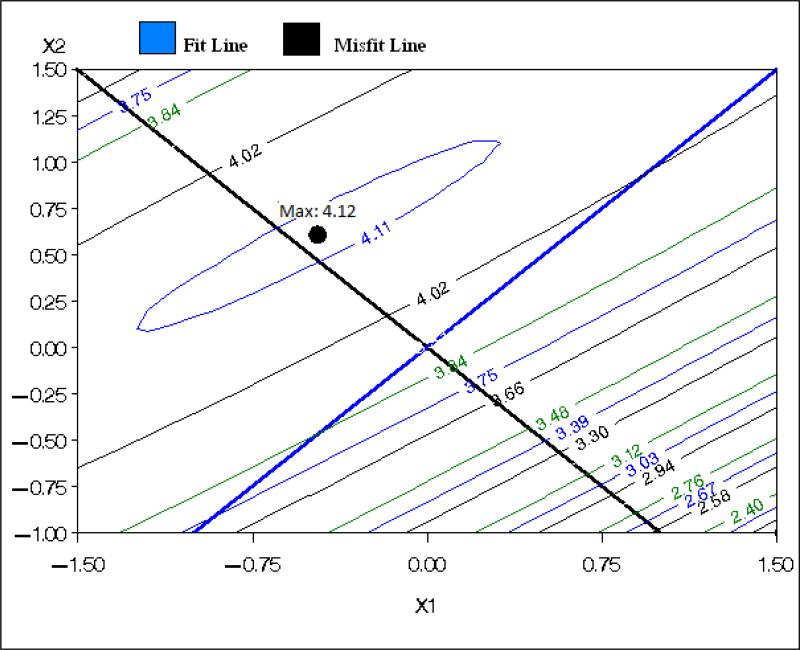
A contour plot displays the curves (or lines), which share the same response value E(Y). The shape of these contours, whether they form ellipses or lines, is determined solely by the second order coefficients: b₁₁, b₂₂, b₁₂. Often, these are ellipses whose center is a function of b₁, b₂. Figure 2 is a contour plot of the estimated response curve displayed in Figure 1, where self-esteem is explained by support received (X₁) and given (X₂).

Figure 2.

Contour Plot Relating Self Esteem to Support Received (X1) and Support Given (X2).

Contour plots are commonly used in the analysis of experimental design, when response surfaces are fitted to study the effect of several factors. In some cases (e.g. Edwards, 2002; Edwards & Parry, 1993), the contours are included as part of the three dimensional plot of the fitted response. Contour plots (in which only the contours are displayed) were seldom adopted as the routine procedure in the application of polynomial regression for congruence analysis. Both Figures 1 and 2 display the fitted polynomial regression model of our supportive exchanges example. The main information in Figure 1 relates to the shape of the response, but it is difficult to figure out what values of the response are expected when the predictors have certain specific values that are of interest (e.g., along the fit or the misfit line). This information can be easily obtained from the contour plot (Figure 2). More specifically, we can see that there is variation in the expected values of self esteem (Y) along the misfit line (values are ranging from around 3.60 to 4.10), while the expected values along the fit line are more stable (ranging from 3.86 to 4.04). The plot also shows that the response is slightly increasing as we move from left to right along the fit line. When we move along the line of misfit, we see that the response is increasing as support given (X₂) increases and support received (X₁) reduces, until it reaches an optimum and then drops down. As expected (due to the significant negative curvature on the misfit line), we also see that the downward trend of the response gets steeper as we go further from the (0, 0) point along this line. We can thus conclude that the difference between support received and given play a greater role in predicting employee self-esteem than the level of the two constructs.

Plots such as Figures 1 or Figure 2 describe the fitted response values, but they do not reveal any information about their accuracy. The analogy of these plots, if we refer to simple linear regression, would be a plot of the fitted line without considering the associated confidence interval. In the following sections, we introduce plots which display the predicted values of the response, as well as their confidence intervals.

Confidence Intervals for the Response along the Fit and Misfit Lines

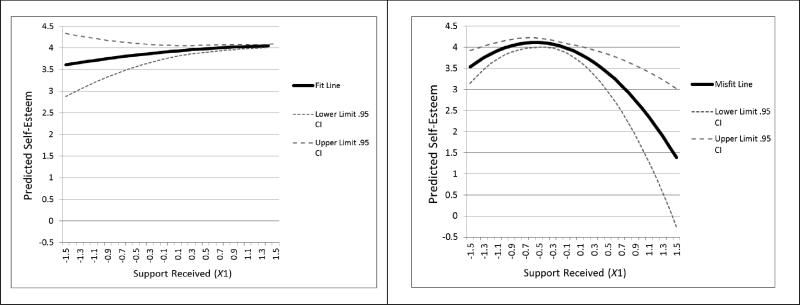
It is a relatively simple statistical procedure to derive for any given (X₁, X₂) values, the predicted response f̂(X₁, X₂) and its .95 confidence interval. For instance, in SAS, the functions LCL and UCL (Lower/Upper bound of a 100(1-α)% CI for a prediction) can be specified in the OUTPUT statement as part of the REG procedure. Figure 3 displays the predicted response values and their associated .95 confidence bands, both along the lines of fit (dashed line) and of misfit (solid line).

Figure 3.

Predicted Response Values for the Lines of Fit and Misfit and Their Associated .95 Confidence Intervals

As expected, we can see that the response is rather constant along the line of fit, indicating that when support received (X₁) equals support given (X₂) (i.e., there is congruence between receiving and giving support), employee self esteem does not significantly change as a function of the amount (i.e., level) of support received/given. In other words, there is no significant difference in employee self esteem between low levels of matched support received and given (low quality reciprocal supportive exchanges), and high levels of matched support received and given (high quality reciprocal supportive exchanges). These results are in line with the coefficients-based hypotheses tested above, which indicated that the slope as well as the curvature along the line of fit does not differ significantly from zero.

Along the line of misfit, we can see that the response varies as a function of the level of incongruence (i.e., difference) between support received (X₁) and given (X₂). More specifically, giving more support (X₂) than receiving (X₁), (X₁<0, hence X₂ >0) seems to be associated with higher self-esteem relative to receiving more support (X₁) than giving (X₂) (X₁>0, hence X₂<0). Moreover, as the level of support received decreases on the misfit line (thus the level of support given increases), the self esteem of an employee enhances. However, when the mismatch reaches the point where support given and support received equal 0.5, -0.5 respectively, the response starts to drop down in the direction where support given increases and support received reduces. Still, based on the CI of the line of misfit we can conclude that this drop down is insignificant.

When comparing the line of fit and the line of misfit, we can see that the response at the line of fit is not significantly different from the response at the line of misfit where support given exceeds support received (i.e., where there is incongruence, such that the exchange of support is under-reciprocating). Yet, the response along the line of misfit where support received exceeds support given (i.e., where there is incongruence, such that the exchange of support is over-reciprocating) seems to be significantly lower relative to the response along the line of fit. These results partially support Hypothesis 1a, which suggests that employee self-esteem reduces to the extent that there is incongruence between support received (X₁) and given (X₂) (i.e., to the extent that the difference between receiving and giving support increases). Although we found that self-esteem reduces to the extent that support received exceeds that given (i.e., there is greater incongruence, such that the exchange of support becomes more over-reciprocating), there is not enough evidence to suggest that self-esteem reduces to the extent that support given exceeds that received (i.e., there is greater incongruence, such that the exchange of support becomes more under-reciprocating). In fact, we found no differences in the self-esteem of those employees who receive and give equal levels of support, and those giving more support than they receive.

An alternative presentation of the polynomial regression model

In this section we consider the quadratic regression model where instead of (X₁, X₂) the two explanatory variables are $D=\frac{X_1-X_2}{2}$ and $M=\frac{X_1+X_2}{2}$, If the main purpose of the analysis is to study the effect of congruence, then the regression coefficients of this alternative model (equation 15) may be easier to interpret, and so is the inference based on it.

$$Y=b_0+b_{D}D+b_{M}M+b_{DD}{D}^2+b_{MM}{M}^2+b_{DM}DM+e.$$ (15)

By applying this transformation, which we refer to as the Difference and Mean Model (DMM), we replaced the original coordinate system (X₁, X₂) by a new system in which D and M are the coordinates. The effect of the difference score (D) on the outcome may depend on the mean of X₁ and X₂ (M). The interaction of D and M in (15), expresses this dependence. Cheung (2009) refers to M as the level and to 2D as the congruence.

One can easily derive the relationships between the regression coefficients in (1) compared with those in (15).

$$\begin{array}{cc}\hfill & b_1=\frac{b_D+b_M}{2}{b}_2=\frac{b_M-b_D}{2}\hfill \\ \hfill & b_{11}=\frac{b_{MM}+b_{DD}+b_{DM}}{4}{b}_{22}=\frac{b_{MM}+b_{DD}-b_{DM}}{4}{b}_{12}=\frac{b_{MM}-b_{DD}}{2}\hfill \end{array}$$

Using (15) is somewhat more straight forward in addressing questions relating to congruence and incongruence. Consider for example, the hypothesis test: b_D = b_DD = b_DM = 0, according to which the outcome depends only on the mean of support received and given. The expected response on the fit line under this hypothesis is expressed as the second degree polynomial in M: b₀ + b_MM + b_MMM². This polynomial expresses the dependence of the slope and curvature of the response on the matched value along the line of fit. Under the additional hypothesis b_M = b_MM = 0 and under the hypothesis: b_M = b_MM = b_DM = 0, the outcome depends only on the difference between support received and given.

The expected response on the misfit line is a second degree polynomial b₀ + b_DD + b_DDD², and if b_D = b_DD = 0 it is constant along the line of misfit. Under the hypothesis b_D = b_M = b_DM = 0 (i.e., the linear coefficients and the cross product coefficient are zero), the model should only include the two second degree terms of D and M. It then means that the fit and misfit lines are the principal axes of the response and the (0, 0) point (which is the point of mid-scales), is the stationary point.

The mean and difference were previously used as predictors by Cheung (2009), who introduced a latent congruence model (LCM), based on Structural Equation Modeling (SEM). LCM takes measurement error into account by treating the components as first order factors with loadings on second order factors (level and congruence). The main drawback of this approach is that it is based on linear relationships unlike the polynomial models which capture curvilinear relationships (Edwards, 2009). In this sense, our approach, which resembles Cheung's method by considering the average and difference as predictors, allows for curvilinear relationships. Table 4 presents the estimated coefficients based on model (15). We can see that the first (b_D = -0.72, p<0.01) and the second order (b_DD = -0.65, p<0.001) coefficients of the difference are significant, while the first (b_M = 0.15, ns) and second order (b_SS = -0.04, ns) coefficients of the mean are not, and neither is the interaction between the difference and the mean (b_DM = 0.26, ns). Accordingly, self-esteem is explained by the difference between support received (X₁) and given (X₂) regardless of their level.

Table 4.

Results of the Difference and Mean model:

Effect	Estimate	SE
Intercept	3.92***	0.07
M	0.15	0.12
D	-0.72**	0.25
M2	-0.04	0.06
D2	-0.65***	0.20
D*M	0.26	0.19
R-square	0.02

According to Table 5, which presents the hypotheses test results on subsets of the coefficients based on the fitted DMM, we can reject the hypothesis b_D = b_DD = b_DM = 0, but we cannot reject b_M = b_MM = b_DM = 0. This means that self esteem depends solely on the difference between support received and given. We can also reject b_D = b_DD = 0, meaning that self-esteem is not constant along the line of misfit between support received and given. Rejecting the hypothesis b_D = b_DD = b_DM = 0 indicates that the lines of fit and misfit are not the principal axes of the response and the stationary point is not the point of mid scale (0, 0).

Table 5.

Hypotheses Tests based on the Difference and Mean model:

Hypotheses:	Num DF	Den DF	F Value	Pr > F
bD=bDD=bDM= 0	3	998	4.47	0.004
bM=bMM=bDM= 0	3	998	1.02	0.38
bD=bDD= 0	2	998	5.56	0.004
bM=bMM= 0	2	998	1.45	0.23
bD=bM=bDM= 0	3	998	4.77	0.003

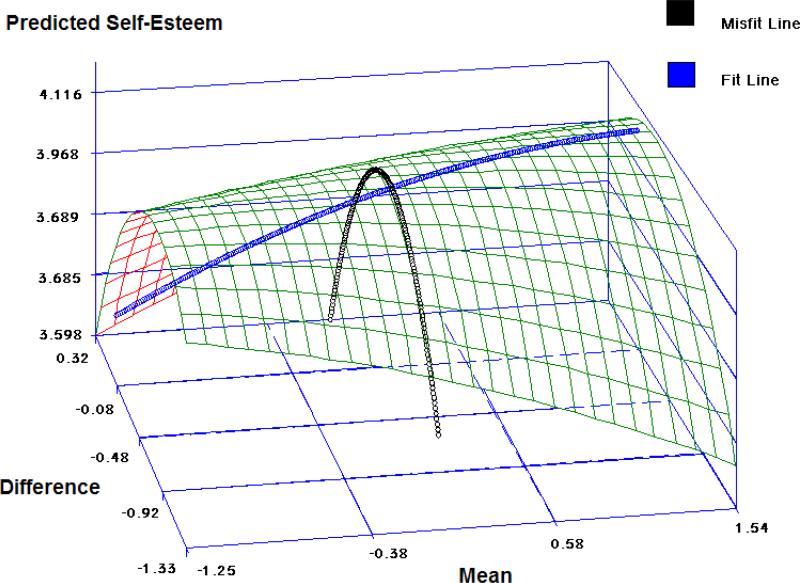
These results can be further illustrated by plotting the surface based on the DMM (Figure 4). The presentation in Figure 4 also includes the location of the lines of fit (blue) and misfit (black) on the three dimensional surface. Such presentation makes the interpretation of the plot much easier, and improves our understanding of the inferences based on the model.

Figure 4.

Surface Plot of the Difference and Mean Model

In Figure 4, we can see that while the response changes only slightly along the line of fit, it has a parabolic shape along the line of misfit. Along the line of misfit, the response increases as support received increases, while support given decreases, but then it starts to drop down at a point where support received slightly exceeds that given. In general, we can see that while self-esteem slightly changes as a function of the mean of support received and given, it changes dramatically as a function of the difference between these two constructs.

Moreover, Figure 4 further indicates that hypothesis 2a, suggesting an increase in self-esteem to the extent support given exceeds that received (the supportive exchange is more under-reciprocating), cannot be supported. It is now clear that self-esteem reduces to the extent that support given exceeds support received. Still, as noted in our inference based on the fit and misfit lines, there is not enough evidence to conclude that greater incongruence where support given exceeds that received (such that the exchange of support is more under-reciprocating), is associated with lower self-esteem relative to smaller incongruence where support given exceeds that received (such that the exchange of support is less under-reciprocating). Accordingly, the results do not fully support hypothesis 1a which suggest that self-esteem reduces to the extent that there is incongruence between giving and receiving support.

Discussion

The aim of the current study was to gain additional insight as to the use of polynomial regression in the behavioral and social sciences. We elaborated on the meaning and the inference based on the coefficients obtained by applying polynomial regression and explained the mathematical terms that are often used to describe response surfaces (e.g. curvature, stationary point, principal axes and eigenvalues).

We introduced additional inference methods and illustrated their application on a real life example from the area of supportive exchanges. We discussed the added value of these methodologies to the inference based on polynomial regression, explaining how each method clarifies different aspects concerning the extent to which the congruence and the incongruence between two constructs (X₁, X₂) predicts the response (Y).

More specifically, we explained how hypotheses testing concerning the slope and the curvature along the lines of fit and misfit can be used for determining the extent and nature of variation in the response along lines that capture congruence and incongruence between the two constructs of interest (X₁, X₂). We also discussed how contour plots may add to the three dimensional surface plot, by providing a clear picture of the fitted expected values of the response and their variation along the lines of fit and misfit. Although contour plots may not improve our ability to make an inference concerning the joint effect of X₁ and X₂ on the response, they nevertheless present the response in a way that provides better understanding of its variation as a function of the two constructs of interest.

We demonstrated how confidence intervals can be used to statistically infer about the values of the response along the fit and misfit lines. This approach can also be used to make an inference concerning the response along any other line of theoretical interest.

Finally, extending previous work of Cheung (2009), we presented the difference and mean model (DMM), which enables to determine the extent to which the difference between the two constructs as well as their mean play a role in predicting the response.

The supportive exchanges example used in the current study for illustrating the methods, highlights the advantage of polynomial regression is addressing more complex research questions concerning the joint effect of two contracts on an outcome. While other approaches (e.g., difference score) seem to be limited in their ability to address questions relating to both the difference between and the level of support received and given, using polynomial regression and additional inference methods we were able to address these questions in a way that highlights the need to develop alternative explanatory frameworks for capturing the effect of supportive exchange patterns on self-esteem (e.g., overreaching frameworks aiming to integrate the two competitive approaches implied by equity-theory and esteem-enhancement theory; see Nahum-Shani et al., 2010). However, since our real life example was driven by illustrative, rather than substantive purposes, we did not include a series of control variables relevant to this type of analysis (see Nahum-Shani et al., 2010). This explains why such low R-square values were obtained for our first-order and polynomial model (Table 2). Still, a 2% increase in R-square from a first-order model to a polynomial model is consistent with the full analysis presented in Nahum-Shani et al., (2010) with respect to depressive and somatic symptoms as the outcomes.

There are still a number of important aspects concerning polynomial regression that warrant the attention of future research. First, consider applying this method with respect to hypotheses which suggest that a moderator (e.g. gender, personality characteristics etc.) may amplify or suppress the effect of congruence or incongruence on an outcome. In such cases, the model becomes highly complex, involving third order interactions which are more difficult to interpret. Moreover, organizational researchers are increasingly interested in examining the congruence between two multilevel constructs, for example between employees’ values (level 1) and organizational values (level 2). Yet little research attention was given to exploring multilevel polynomial regression (see Jansen and Kristof-Brown, 2005) and the presentation and interpretation of this method remains relatively under-studied. This highlights the need to explore more complex theory driven polynomial regression models and to expand its application in congruence research.

Finally, as noted earlier, in most of the studies based on polynomial regression (e.g., Jansen and Kristof-Brown, 2005) the tested hypotheses are formulated as null hypotheses such that they are supported when obtaining no significant results. Researchers should take into account that such hypotheses testing requires sufficient power (either with a large sample and/or relatively large size effects) so that the hypotheses will not be wrongly supported, (which is an error of the second kind).

In sum, we hope our discussion of additional inference methods would increase the extent to which polynomial regression is used in the social and behavioral sciences for advancing theory concerning the effect of congruence and incongruence as well as for addressing other research questions concerning to the joint effect of two constructs.