Characterizing accuracy of total hemoglobin recovery using contrast-detail analysis in 3D image-guided near infrared spectroscopy with the boundary element method

Abstract

The quantification of total hemoglobin concentration (HbT) obtained from multi-modality image-guided near infrared spectroscopy (IG-NIRS) was characterized using the boundary element method (BEM) for 3D image reconstruction. Multi-modality IG-NIRS systems use a priori information to guide the reconstruction process. While this has been shown to improve resolution, the effect on quantitative accuracy is unclear. Here, through systematic contrast-detail analysis, the fidelity of IG-NIRS in quantifying HbT was examined using 3D simulations. These simulations show that HbT could be recovered for medium sized (20mm in 100mm total diameter) spherical inclusions with an average error of 15%, for the physiologically relevant situation of 2:1 or higher contrast between background and inclusion. Using partial 3D volume meshes to reduce the ill-posed nature of the image reconstruction, inclusions as small as 14mm could be accurately quantified with less than 15% error, for contrasts of 1.5 or higher. This suggests that 3D IG-NIRS provides quantitatively accurate results for sizes seen early in treatment cycle of patients undergoing neoadjuvant chemotherapy when the tumors are larger than 30mm.

1. Introduction

Optical near infrared (NIR) imaging provides a non-invasive method of probing functional status of tissue in-vivo and has been used for studying breast [1, 2, 3], brain [4, 5], skin [6], prostate [7], finger joints [8, 9] and other tissues [10]. The primary parameters of interest in NIR imaging are concentrations of oxy-hemoglobin [HbO] and deoxy-hemoglobin [Hb], water, lipids and scattering parameters which provide contrast between healthy and diseased tissues. Extended indices such as total hemoglobin concentration [HbT] and oxygen saturation (StO2) are derived from these parameters. In the context of breast imaging, studies have shown that [HbT] provides a consistent parameter for contrast between lesions and healthy tissue [1, 11, 12, 13, 14, 15, 16]. In a review of optical imaging studies from approximately 2000 subjects, Leff et al [11] showed that breast lesions contain approximately twice [HbT] compared to background. In a breast cancer detection study with 116 subjects, Chance et al [1] showed that NIR spectroscopy had sensitivity of 96% and specificity of 93% with area under curve of 95% using [HbT] and StO2 as metrics. Notably for patients undergoing neoadjuvant chemotherapy (NACT), Jiang et al [17] demonstrated that [HbT] was statistically significant in predicting full response to chemotherapy. Also subjects responding to the treatment showed a significant drop in [Hb] as compared to non-responders [18]. These studies used a combination of spectroscopy and tomography approaches.

Although images obtained from NIR tomography demonstrate useful functional characterization, they have poor spatial resolution when compared to conventional imaging methods. For 2D images, it has been shown that 85% accuracy in recovering optical characteristics of anomalies is achievable if their size is 25mm, while one should expect lower accuracy, i.e. 75%, when at a size of 17mm [19]. In the 3D case, for 8mm lesions, researchers reported that a mere 15% of the expected values could be reconstructed [20], and this is often attributed to the higher level of ill-posedness of the inversion problem when using a full 3D model. This is one of the main issues examined here, which is how to maximize the contrast recovery in 3D imaging, implementing prior information and homogeneous region constraints.

The way to advance this approach is through recognition that standard clinical imaging techniques such as MR, CT and X-Ray are effective ways of detecting abnormal structures in tissue and so they can provide high resolution maps of tissue borders but they could all benefit from some addition which might add to increased specificity [21, 22]. Using the data from standard imaging as a priori information about the size and location of the tumor enhances the resolution of NIR imaging as shown by different studies [9, 23, 24, 25]. Various ways to incorporate these structural priors have been studied including Bayesian [26], regularization [27] and use of ‘hard priors’ [20, 28]. In the case of hard priors, the tissue under investigation is assumed to contain homogeneous regions whose boundaries are known perfectly. This has shown promise in quantitative accuracy and is akin to image-guided NIR spectroscopy of deep tissue volumes [20, 29]. In 3D, this provides a bulk average estimation of each tissue type or region in the domain. Dehghani et al [20] show that hard priors improved calculation of absorption and scattering values to within 97% and 93% of expected values for spherical inclusions in a cylindrical domain. Others have performed similar studies on case-by-case basis [28, 30, 31]. Expanding upon this idea, there is a need to understand the accuracy in quantification of [HbT] in this multi-modality setting, using a wide range of tumor sizes and contrasts, which provides full interpretation of the contrast-detail performance of the combined system. This is especially important as we move into studying response to NACT where tumor sizes and contrasts change with treatment, and understanding how [HbT] varies with changes in tumor size is especially important.

Image reconstruction requires a model for light propagation in tissue, and diffusion equation has commonly been used for this [32, 33] and the finite element method (FEM) has been used to solve the model [34, 35]. While being very flexible in terms of shape of the domain of the problem, FEM requires discretization of the entire volume of domain, which makes it a computationally intensive method in 3D. Srinivasan et al [36] have successfully implemented a boundary element method (BEM) approach which is geared towards hard priors. BEM modeling only requires surface discretization of the defined homogenous regions, which greatly reduces the meshing and grid generation complexities of the clinical applications. Compared with the 3D FEM method, there is a 44% to 72% reduction [36] in computation time for meshing and forward model steps in the BEM approach for a two-region problem.

In this work, we characterize the accuracy of 3D IG-NIRS with BEM under the assumption of hard priors in quantifying [HbT] of breast tumor and its contrast relative to background tissue using contrast-detail analysis. Using a 3D breast mesh (which is constructed from MR images of a breast phantom), sets of simulations are carried out to study effects of tumor size and contrast. The recovery of [HbT] contrast with and without water contrast is studied, and also the meshing resolution is optimized. Use of partial volume meshes for improving quantification is also detailed.

2. Method

2.1. Overview

Contrast-detail analysis has commonly been used to describe medical imaging systems [37, 38, 39, 40]. This type of analysis evaluates the performance of the imaging system by producing a series of images for a range of clinically relevant contrasts and sizes within a domain, with focus on characterizing the lower limits of the imaging technique. This is used to determine the detectability of an object with a given size and contrast. Here, we have used a modification of this technique, with focus on quantification rather than detection, so that the accuracy in quantifying [HbT] could be studied. For this purpose, series of simulations were carried out simulating a range of inclusion sizes found in many clinical settings. The study was performed for non-spherical and spherical inclusions. Using MR images of a breast phantom modeled from clinical breast MRI, a 3D surface mesh was created using Mimics [41] after image segmentation to represent the exterior boundary of the model. This imaging domain and the 3D surface along with location of 16 sources and detectors are shown in Figure 1.

Fig. 1.

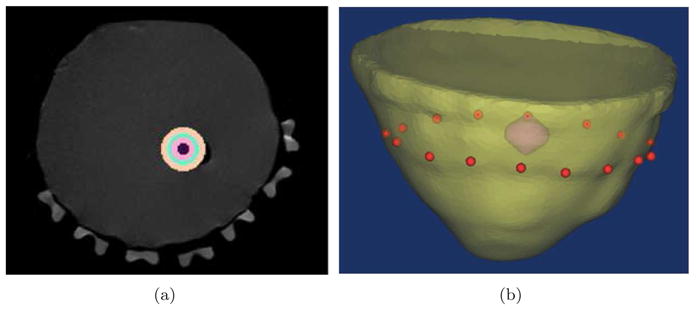
In (a) the MR image of a breast phantom is used to generate the surface of breast shown in (b), which is a 3D rendering of the mesh with inclusion and the position of source/detectors in red dots.

2.2. Diffusion Modeling and Reconstruction

Light propagation was modeled using diffusion approximation to the radiative transport equation:

$$-\nabla ·D(r)\nabla \mathrm{\Phi }(r,\omega )+\left({\mu }_a(r)+\frac{i\omega }{c}\right)\mathrm{\Phi }(r,\omega )=q_0(r,\omega )$$ (1)

where D(r) is the diffusion coefficient, Φ(r, ω) is the fluence at modulation frequency ω and location r, μ_a is the absorption coefficient, c is the speed of light and q₀ is an isotropic source. The diffusion equation is valid under the assumption that elastic scattering dominates over absorption (which is true for breast tissue), and at distances larger than one scattering distance from the source. In this approximation, the fluence distribution is considered to be predominantly isotropic. The boundary element method was used to solve this partial differential equation under the assumption that the breast can be estimated as piece-wise continuous domains with homogeneous regions, whose boundaries are known a priori. The BEM approach provides an efficient method for 3D recovery by reducing the dimensionality of the problem, utilizing a prior knowledge of Green’s function of the diffusion equation. Details of this implementation can be found elsewhere [36, 42].

Using the BEM-based near infrared spectroscopy toolbox [36, 43], we performed image reconstruction for a range of contrasts for [HbT] and size distribution of anomalies within the breast. This involved a two-step process:

1. Boundary measurements of light fluence at six different wavelengths (661, 761, 785, 808, 826 and 849nm, consistent with the experimental system [44]) were calculated using the BEM model for diffusion equation. Absorption (μ_a) and scattering ( ${\mu }_s^{\prime }$) coefficients for the model were calculated using modified Beer-Lambart law based on concentration values from Table 3. The boundary measurements consisted of amplitude and phase at frequency of 100 MHz at the detector locations at six wavelengths in the NIR regime. A 5% random Gaussian noise was added to the boundary data based on typical noise level found in the experimental system.

   In this step we used the resulting boundary measurements to solve the inverse problem and recover NIRS parameters [HbO], [Hb], [Water], [HbT], [StO2] and scattering parameters (amplitude a and power b) for background and inclusion. This was done using direct spectral image reconstruction on multi-wavelength measurements, assuming the spectral signatures of the chromophores were known as a priori [45, 46, 47]. The inverse problem was solved using a modified Newton’s method with Levenberg Marquardt regularization [35] and yielded values for the NIRS parameters for each of the regions of the breast.

Table 3.

Level of oxy-hemoglobin (HbO), deoxy-hemoglobin (Hb) and HbT in different simulated contrast ratios (μM)

HbT ratio	1.0	1.25	1.50	1.75	2.0	2.25	2.50	2.75	3.0
HbO	8.4	10.5	12.6	14.7	16.8	18.9	21.0	23.1	25.2
Hb	5.6	7.0	8.4	9.8	11.2	12.6	14.0	15.4	16.8
HbT	14.0	17.5	21.0	24.5	28.0	31.5	35.0	38.5	42.0

2.3. Simulation Study Parameters

Two sets of inclusions representing tumors within the breast were created to conduct the simulations:

Non-spherical Inclusions

Six inclusions at different sizes were created inside the breast mesh to represent hypothetical tumors. These inclusions did not posses regular geometrical shapes in order to specifically test recovery with these asymmetric situations. Information about volume, surface area and mesh properties are listed in Table 1. Also included in the same table is an equivalent diameter of the inclusion that is calculated using a sphere that would contain the same volume as the ellipsoid inclusion.

Table 1.

Size and mesh properties of non-spherical inclusions used in the simulations. Equivalent diameters is diameter of a sphere that would contain the same volume as the inclusion.

	Elems.	Nodes	Vol.(mm3)	Surf.(mm2)	Surf. ratio(%)	Eq. dia(mm)
1	1474	739	1949	783	2.2	16
2	1556	780	2668	964	2.7	17
3	2374	1189	3709	1221	3.4	19
4	2426	1215	4793	1444	4.0	20.9
5	3006	1505	7774	2011	5.6	24.6
6	3786	1895	19369	4035	11.2	33.6
Breast	9430	4717	502930	36036	100.0	100

Spherical Inclusions

For consistency with typical contrast-detail plots, spherical inclusions were also simulated and recovery of IG-NIRS parameters for these were studied. The size and mesh properties are given in Table 2.

Table 2.

Size and mesh properties of spherical inclusions used in the simulations and contrast-detail plots.

	Elems.	Nodes	Vol.(mm3)	Surf.(mm2)	Surf. ratio(%)	Dia.(mm)
1	242	480	93	103	0.29	5.6
2	482	960	275	211	0.59	8.1
3	503	1002	619	360	1.00	10.6
4	520	1036	1220	555	1.54	13.3
5	722	1440	2055	786	2.19	15.8
6	1065	2126	4636	1355	3.77	20.7
7	1312	2620	8972	2094	5.82	25.8
Breast	9430	4717	502,931	36,036	100.0	100

Contrast Values Relative to the Background Tissue

Based on literature [11], [HbT] for background (breast) tissue was set at 14μM [48, 49]. [HbT] in the inclusions was calculated such that the ratio of inclusion relative to the background value varied from 1.25 to 3.0 in a step of 0.25. Table 3 shows all the contrast ratios along with the values for [HbO], [Hb] and [HbT] using 60% of oxygen saturation. This reflects the typical range of contrasts found in clinical data [11]. For the first set of simulations, it was assumed that the contrast between tumor and the background was only due to HbT; leaving water and scatter parameters identical in breast and inclusion. In the second set of simulations, water contrast was added, as a way to systematically study its added effect.

3. Results

3.1. Non-Spherical Inclusions

3.1.1. Contrast-Detail Plots

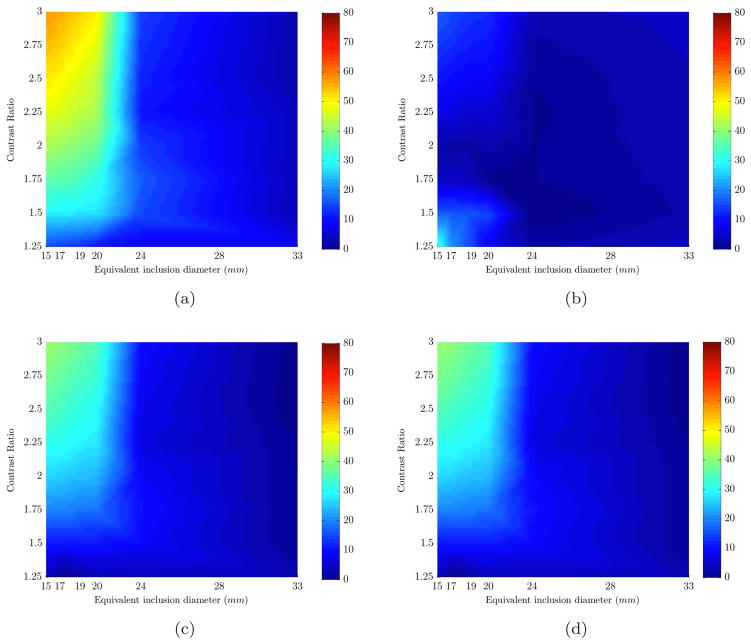
The results from the entire range of sizes and contrasts are summarized in contrast-detail plots with color map showing the error in recovery (Figure 2). In these plots, the X axis is the equivalent size of the inclusion and Y axis is the [HbT] contrast between inclusion and background. Any given point in these plots is the error involved in recovering a given value of [HbO], [Hb] or [HbT] for a specific inclusion size and contrast. The error increased for decreasing size of inclusions as expected and higher error was found in [HbO] recovery than the rest. This is likely because the spectral features of [HbO] could not be accurately de-convolved from water in the range of wavelengths used in the simulations. The error for water content value was less than 2% and for scattering parameters it was less than 21%. The error in recovered background values for water and scattering was less than 1%.

Fig. 2.

Percent error plots (color bar shows error values) are shown for the range of sizes (x-axis) and contrasts (y-axis). Each plot represents the error in recovering an expected value of a different chromophore based on varying sizes (x-axis) and contrasts (y-axis): (a) HbO, (b) Hb, (c) HbT, (d) Contrast Ratio. The results are for non-spherical inclusions with no water contrast.

The average error in quantification of [HbT] in the size range of 24mm to maximum size (33mm) was less than 12%, whereas this error increased to a maximum of 41% in the lower size range of 15 to 24mm. Note that the low errors at low contrasts for small inclusions are due to the fact that the first contrast ratio is very close to initial guesses of reconstruction algorithm, which was given to be the chromophore values of the background.

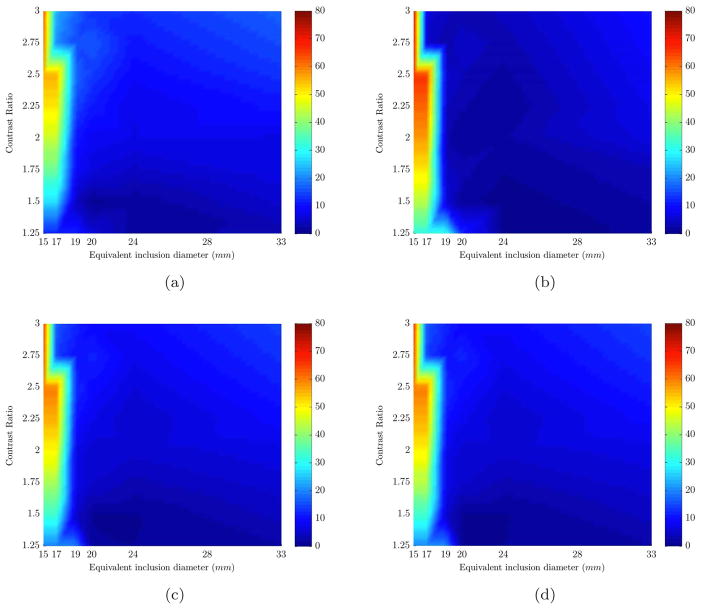
So far, as mentioned before, all simulations assumed that water content of the inclusion and breast was identical to separate error of [HbT] recovery from the rest of chromophores. In the next step, water contrast was included. A second set of 48 simulations was carried out in which the water content of the inclusion and breast were assumed to be 70% and 40% respectively. Figure 3 shows that presence of water contrast between inclusion and background reduces the error in reconstructing [HbT]. The minimum size at which [HbT] error was less than 12% reduced to 19mm from 24mm. However for inclusion sizes smaller than 19mm the error in recovery of [HbT] increased to 66%. The error in recovery of water content for 15 and 17mm sizes was close to 50% but this error drops to an average of 12% for sizes 19mm and up.

Fig. 3.

Percent error plots (color bar shows error values) are shown for the range of sizes (x-axis) and contrasts (y-axis). Each plot represents the error in recovering an expected value of a different chromophore based on varying sizes (x-axis) and contrasts (y-axis): (a) HbO, (b) Hb, (c) HbT, (d) Contrast Ratio. The results are for non-spherical inclusions with water contrast.

3.2. Spherical Inclusions

3.2.1. Contrast-Detail Plots

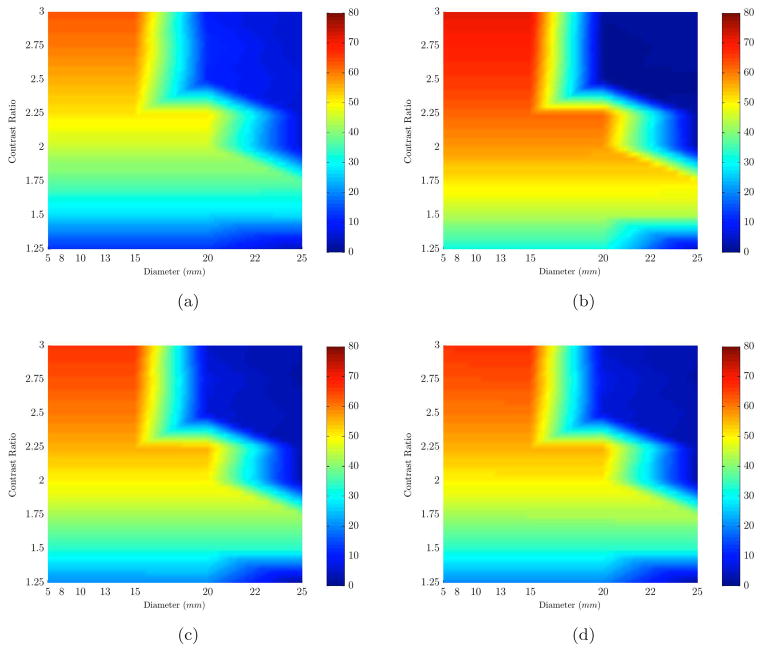
The simulations from previous section were repeated using inclusions which were perfect spheres for consistency with traditional contrast-detail plots. Seven different sizes were created whose diameters were 5.6, 8.1, 10.6, 13.3, 15.8, 20.7 and 25.8mm. Table 2 contains detailed information about the size, mesh resolution and volume of the spheres. A smaller starting size of 5mm is used to expand the range of inclusion sizes studied. The [HbT] in inclusions and breast were the same as before (Table 3) and contrast in the water content (40% in background and 70% in inclusion) was used for all simulations involving spherical inclusions. Scattering parameters were assumed to be the same. Results from reconstructions are shown in a contrast-detail plot in Figure 4. The [HbT] recovery error in the size range of 20mm and up was less than 7% for contrasts ratios of 2.5 and higher, whereas this error increased to 66% for inclusion sizes smaller than 20mm. As expected, the recovery of values for small sizes (below 15mm diameter) was not as accurate as larger inclusions, i.e. error was larger than acceptable maximum of 15%.

Fig. 4.

Percent error plots (color bar shows error values) are shown for the range of sizes (x-axis) and contrasts (y-axis). Each plot represents the error in recovering an expected value of a different chromophore based on varying sizes (x-axis) and contrasts (y-axis): (a) HbO, (b) Hb, (c) HbT, (d) Contrast Ratio. The results are for spherical inclusions (with water contrast) whose sizes were smaller than that of non-spherical inclusions shown in Figures 2 and 3.

3.2.2. Partial Volume Reconstruction

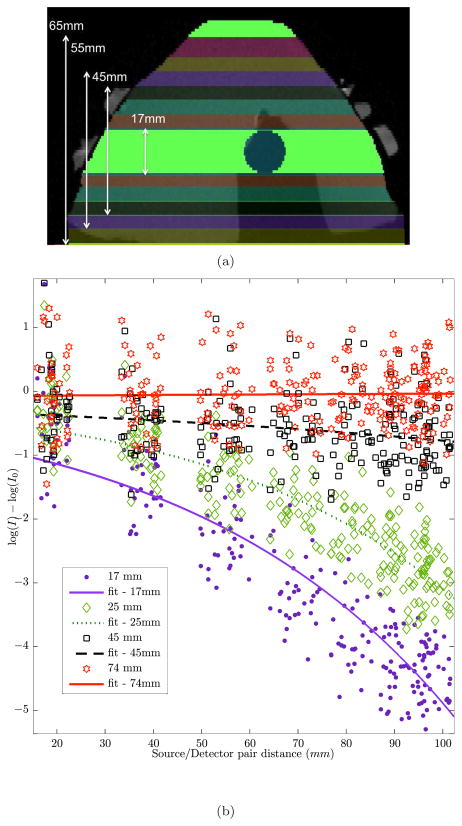
The effect of using a smaller domain for the background (breast) using a partial-volume reconstruction was studied by reducing the height of the breast mesh. The rationale for this was that the inverse problem may be less ill-posed in a partial domain as compared to full 3D. The height of the original breast mesh was reduced in 7 different steps resulting in volumes with total heights of 17, 25, 35, 45, 55, 65 and 74mm, as shown in Figure 5(a). The boundary data from forward model was calculated on a full 3D mesh (as shown in Figure 1) and the reconstruction was carried out using the partial volume meshes. Since changing the size of the mesh alters the boundary conditions of the problem, one needs to investigate the variation of light fluence at detector locations.

Fig. 5.

(a) Different heights from the MR image of the the breast phantom (17, 25, 35, 45, 55, 65 and 74mm) were used to create various sizes for the 3D breast mesh to study the effect of trimmed meshes. (b) Using the full breast mesh as the reference, the change in light fluence of the trimmed meshes (shown in (a)) at the detector locations is shown here. Horizontal axis is the distance between source/detector pairs and vertical axis is the light fluence difference between full mesh (I₀) and partial mesh (I). For clarity not all trimmed sizes are shown. The height of the full breast mesh was 79mm.

Figure 5(b) plots the logarithm of light fluence difference between original full volume and different partial volumes for 785nm wavelength. As expected, the difference increases at further source-detector distances for smaller heights where some light is lost at the boundaries of partial domains. Calculating the standard deviation of light fluence differences revealed that for heights 35mm and up, the perturbation caused by partial mesh is less than the noise (5%) we introduced in simulations (section 2.2) whereas for heights below 35mm, the error increased above acceptable noise threshold.

For comparison with full mesh, the 45mm-tall mesh was chosen for which the differences in the sensitivity matrix was calculated using a metric of condition number of the Hessian (given by J^T J, where J is the Jacobian or the sensitivity matrix). Condition number is directly related to what extent the problem is ill-posed and is given as a ratio of the largest singular value to the smallest singular value, and large condition numbers indicate an ill-conditioned matrix, prone to being singular and susceptible to numerical errors. For a full 3D reconstruction, the condition number of the Hessian was 2.1 × 10⁷ whereas for a partial 3D reconstruction, this was reduced to 7.6 × 10⁶. While both problems were ill-conditioned needing regularization, the partial 3D reconstruction gave a condition number which was lower and hence better-conditioned and better posed.

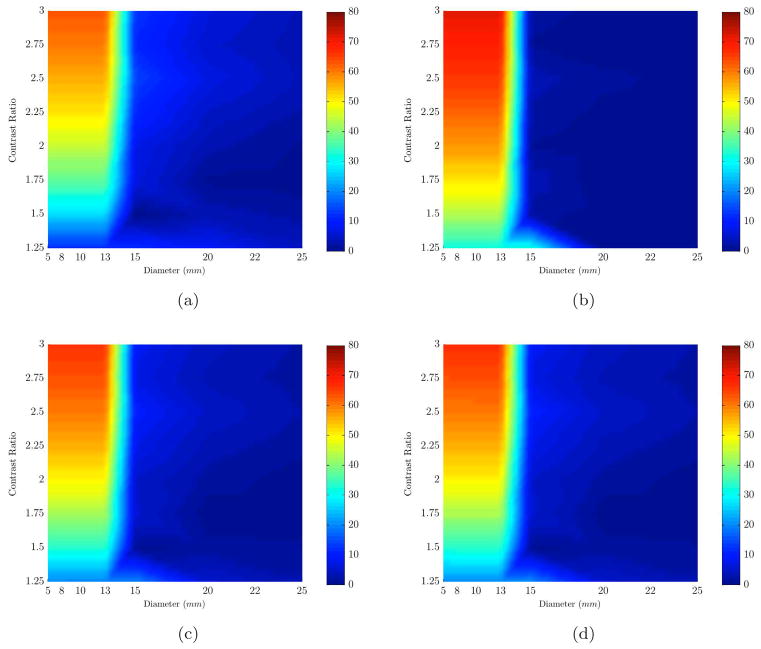
The results shown in Figure 6 indicate that partial volume recovery enhanced our ability to recover [HbO], [Hb], [HbT] and contrast in [HbT] for sizes larger than 13mm in diameter, and also improved the recovery of low contrast inclusions of bigger sizes (in range of 15 to 25mm). Now, the minimum size for which we could recover [HbT] for contrast ratios of 1.25 and above was 14mm (with errors less than 15%). This is an improvement in minimum detectable size from 20mm with a full reconstruction. The main improvement was in contrast ratios of 1.5 to 2.5 in which an average recovery error of 15% was achieved. The partial mesh reconstruction also improved water content recovery of inclusion, reducing the minimum detectable size to 15mm from 20mm for HbT contrast ratios of 2:1 and higher. Also the scattering amplitude parameter was better recovered for sizes of 15mm and higher (down from 25mm) with a maximum error of 5%. The chromophore values recovered for the background (breast) using the partial volume mesh showed minor changes (less than 1%) with respect to those recovered from the full mesh.

Fig. 6.

Percent error plots (color bar shows error values) are shown for the range of sizes (x-axis) and contrasts (y-axis). Each plot represents the error in recovering an expected value of a different chromophore based on varying sizes (x-axis) and contrasts (y-axis): (a) HbO, (b) Hb, (c) HbT, (d) Contrast Ratio. The results are for spherical inclusions (with water contrast) using partial volume type reconstruction with reduced volume for breast mesh as shown in Figure 5(a).

As a general rule, the ratio of the height of mesh to the diameter of the breast at the location of fibers should be roughly 45% or more for accurate results without incorporating artificial errors in the boundary data due to boundary conditions.

3.3. Optimization of Mesh Resolution

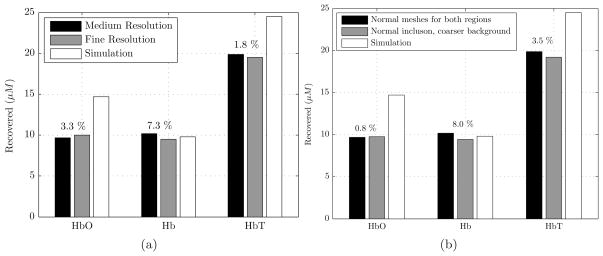
In this part, we studied the effect of mesh resolution on accuracy of reconstruction and computation time. One of the sizes used above (size 3, equivalent diameter of 19.21mm as shown in Table 1) was re-examined with almost doubling the number of nodes (1,189 to 2,061) in the inclusion mesh (Table 4). The breast surface mesh resolution was kept constant. Simulation results for HbT contrast of 1.75 with a high resolution inclusion mesh did not improve recovery of [HbT] showing that the original inclusion mesh (with average edge length of 1.10mm) was an optimal one. Figure 7(a) shows the recovered values for [HbO], [Hb] and [HbT] in the inclusion. The percentage change in [HbT] was less than 2%.

Table 4.

Number of nodes used in different mesh resolution for “size 3” inclusion.

Inclusion Mesh Resolution	No. of inclusion nodes	No. of breast nodes
Fine	1,189	4,717
Extra fine	2,061	4,717

Fig. 7.

(a) Reconstructed estimates of HbO, Hb and HbT concentration are shown for a simulated inclusion with an equivalent diameter of 19.2mm. The resolution of the inclusion mesh was doubled. The difference in HbT was less than 2% using different mesh resolutions. The numbers shown on top of each set of bars are the % error of the medium resolution relative to the fine resolution. Refer to Table 4 for mesh information. (b) Using a relatively coarser mesh for the breast model not only produces accurate chromophore values but also it reduces computational time relative to normal breast mesh. The numbers shown on top of each set of bars are the % error of each chromophore of the coarse breast mesh relative to normal breast mesh. Refer to Table 5 for the mesh information used here.

In another simulation, we used a mesh with coarser resolution for breast to speed up the reconstruction process. To study this, the number of nodes in the breast mesh was reduced by a factor of 2 while keeping the mesh resolution of inclusion constant. This reduced the computational time significantly, Table 5, while recovering almost the same values for [HbO] and [Hb], with a maximum relative error of 8%, Figure 7(b).

Table 5.

Better computational performance is achieved by choosing the mesh as described in section 3.3. The simulations were run on a computer with 32 GB of memory and an AMD Opteron CPU @ 2.7GHz with Linux as operating system.

Background Mesh Resolution	Time (hrs)	No. of nodes (inclusion/mesh)
Medium resolution inclusion/high resolution background	20:00	1189/4717
Medium resolution inclusion/medium resolution background	5:30	1189/2132

While these studies are on a case-by-case basis making it difficult to generalize the mesh resolution required for an optimal imaging in terms of computation time and accuracy, they demonstrate that the mesh resolution used in the simulations was optimized for time and accuracy. For all the simulations presented previously, the breast mesh comprised 2,132 nodes with average edge length of 4.5mm and inclusion surface comprised fine resolution with average edge length of 1.1mm. Results (not shown here) also demonstrated that below a certain resolution, discretization errors started dominating the reconstructed values.

4. Discussions

Multi-modality optical imaging has been shown to improve optical imaging by using spatial priors from other techniques such as MRI during the image-formation procedure [20, 48, 23, 50, 29, 51, 52]. Pogue et al [53] showed that the minimum detectable sizes through 2-D optical NIR imaging were in the range of 1/10th of the outer diameter (of the main object being imaged) with minimum detectable contrast in the range of 10 to 20% of contrast for an object located in the center of the domain; these limits decrease for objects near the surface. Using spatial priors, it has been shown that this minimum size and contrast can be reduced further. This type of analysis was geared towards detection using contrast-to-noise ratio as a metric. In our application, the detection of a lesion will be available from MRI, and the optical technique complements this by providing functional characterization of the lesion.

In this scenario, we aim to answer the question: what is the minimum size and contrast that can be quantified accurately. NIR imaging is based on quantification of magnitudes rather than shapes which is a distinction between optical and other conventional technologies like mammography, ultrasound and MRI which depend primarily on morphological changes [1]. Accurate quantification in this study denotes ability to reconstruct HbT values with less than 15% error. The 15% was chosen empirically based on our ability to quantify phantoms [19] and the intra-subject variability quoted between 13% [54] to 16% [55]. For imaging systems known to have higher levels of uncertainty, this cutoff may be higher. It is to be noted that standardization of these levels is a difficult issue because accuracy demonstrated in phantoms from literature varies widely due to the properties and types of phantoms studied [56] and intra-subject variability also depends on patient age, oral contraception and other factors [57, 58, 59].

An important distinction in this study is that all the simulations are in 3D and in realistic tissue domains (in terms of size and shape), providing accurate and realistic scenario for quantification of [HbT]. A total of 208 3-D simulations were carried out to obtain the contrast-detail plots presented here providing an extensive and systematic study, the first of its kind in 3D to our knowledge. The results showed several trends that are discussed below.

1. The availability of water contrast in optical techniques helps improve the accuracy of recovering [HbO]. This may be due to crosstalk, which is known to be present especially when wavelengths beyond 850mm are not used. HbO and water have similar spectra in the wavelength range used in this study and addition of water contrast results in some cross-talk or bleed-through into [HbO]. Indeed, studies on improving water quantification both through simulations [60, 61] and experiments [62, 63, 64, 65] have shown that longer wavelengths, beyond 850nm, are necessary. However, wavelength availability in the frequency domain (FD) instrumentation is limited by response of photomultiplier tubes and moving towards a hybrid FD-CW system may be optimal for better quantification of water [62, 64].

2. Results from non-spherical inclusion diameters showed better quantification than spherical inclusions of the same sizes. The reason can be that these inclusions are ellipsoid shapes with longer size on the plane of measurement, hence positioning bigger portion of the inclusions within the sensitivity zone of NIRS. Thus the equivalent diameter may underestimate the actual diameter in the plane of the optical fibers (the equivalent diameters were calculated using a sphere with the same volume as inclusion). So an important conclusion is that the accuracy in recovery is dependent upon the spatial extent of the tumor within the zone of sensitivity of NIR.

3. Use of a reduced 3D exterior volume for reconstruction reduced the minimum quantifiable size from 20mm to 14mm (roughly to 1/15^th of breast diameter). In a finite element reconstruction, use of fewer numbers of unknowns in the recovery reduces the ill-posed nature of the problem. In the boundary element reconstruction, the fundamental solution is given by Green’s function for modified Helmholtz equation:

   $$\frac{exp(-\lambda ·r)}{4\pi ·D·r}$$ (2)

   where r is the distance between any two nodes and

   $$\lambda =\sqrt{\frac{{\mu }_a+i\omega /c}{D}}$$ (3)

   Thus Green’s function decreases exponentially with distance so that the contribution to Green’s function should be negligible from nodes at large distances from each other. This indicates that the image reconstruction on a partial domain may reasonably approximate the solution depending on the distances involved. In the current study, the difference in boundary measurements between a full 3D versus partial 3D volume was less than 5% for both intensity and phase values for domains of heights 35mm or more, which is below the noise threshold. Within this framework, the condition number gives an indication of how ill-conditioned the problem was. It was found here that for the partial mesh, the condition number was an order of magnitude lower than the full mesh.

4. These results indicate that the changes found earlier during NACT are likely to be quantified accurately. It is well known that patients treated with NACT have large solid tumors. The tumor size distribution before NACT depends on surgical procedure (Mastectomy/Lumpectomy) and has been quoted to range in 26–85mm [66] from study on 76 subjects. This is well within the range of accurate quantification using IG-NIRS. Since there is a significant need in characterizing the response of a subject to NACT as early on in treatment as possible, our results indicate that IG-NIRS may fulfill a key role in this process by providing quantitative and functional information for the relevant tumor sizes.

5. Conclusions

In summary, we have presented a detailed contrast-size analysis to quantify chromophores such as [HbT] in 3D breast models for a range of tumor sizes and contrasts and the results show that tumors as small as 14mm can be quantified with accuracy of 85% (and higher) with IG-NIRS using BEM. Reducing the entire mesh size had a beneficial effect upon the recovery of the properties, such that an optimal size of the breast mesh allows accurate recovery of chromophores within inclusions whose size is nearer 1/15^th of the breast diameter, and the ideal mesh height appears to be about 45% of the breast diameter. Image-guided NIRS complements traditional techniques such as MRI by providing additional functional information for diagnosis and treatment monitoring. Ongoing work is examining the use of this technique in in vivo clinical trials monitoring response to NACT.