How Accurate Is Peer Grading?

Abstract

Previously we showed that weekly, written, timed, and peer-graded practice exams help increase student performance on written exams and decrease failure rates in an introductory biology course. Here we analyze the accuracy of peer grading, based on a comparison of student scores to those assigned by a professional grader. When students graded practice exams by themselves, they were significantly easier graders than a professional; overall, students awarded ≈25% more points than the professional did. This difference represented ≈1.33 points on a 10-point exercise, or 0.27 points on each of the five 2-point questions posed. When students graded practice exams as a group of four, the same student-expert difference occurred. The student-professional gap was wider for questions that demanded higher-order versus lower-order cognitive skills. Thus, students not only have a harder time answering questions on the upper levels of Bloom's taxonomy, they have a harder time grading them. Our results suggest that peer grading may be accurate enough for low-risk assessments in introductory biology. Peer grading can help relieve the burden on instructional staff posed by grading written answers—making it possible to add practice opportunities that increase student performance on actual exams.

INTRODUCTION

Students do better on exams when they have a chance to practice. For example, instructors in introductory chemistry, mathematics, and physics routinely assign problem sets or other types of weekly homework; randomized, controlled trials have shown that student performance improves when these types of exercises are required (Marr et al., 1999; Trussell and Dietz, 2003; Cheng et al., 2004). Across the science, technology, engineering, and mathematics (STEM) disciplines, frequent quizzing or pop-quizzing has also been shown to increase student achievement on exams (Barbarick, 1998; Graham, 1999; Klionsky, 2002; Leeming, 2002; Steele, 2003; Daniel and Broida, 2004; Margulies and Ghent, 2005; Casem, 2006; but see Haberyan, 2003). Even a single practice exam can help (Balch, 1998).

Mandatory practice is beneficial, but there is a catch: someone has to grade the exercises (Paré and Joordens, 2008). When budgets for instructional resources are under pressure, it may not be possible to assign homework, problem sets, quizzes, or other instruments that must be graded by an instructor, graduate teaching assistant, tutor, or other expert.

Long before the recent reductions in higher education budgets, however, researchers began exploring self-assessment, peer-assessment, and other forms of nontraditional evaluation. Initially, most researchers were interested in the use of peer review to improve writing across the undergraduate curriculum. But in the natural sciences, interest began to focus more on 1) the possible benefits of self-assessment in the development of reflective and meta-cognitive skills, and 2) emphasizing peer-assessment as an important skill in professional practice (Topping, 1998; Sluijsmans et al., 1999). Understanding and implementing peer review, for example, was seen as a legitimate course goal, given its importance in academic research and in establishing referral patterns in clinical settings (Evans et al., 2007). Interest was strong enough to inspire the development of at least two widely used online systems for implementing self- or peer-review in college courses: the Calibrated Peer Review system written and maintained at University of California, Los Angeles (Robinson, 2001) and the peerScholar software created at the University of Toronto (Paré and Joordens, 2008).

Can peer grading effectively assess student performance on homework, problem sets, quizzes, practice exams, or other types of exam-preparation exercises? If so, then peer grading might make these types of assignments practical for large-enrollment courses, even when staffing levels decline.

Earlier we showed that weekly, timed, and peer-graded practice exams helped improve performance in an introductory biology course for majors that enrolled 340 students (Freeman et al., 2007). Working with a human physiology course for undergraduate nonmajors, Pelaez (2002) also documented a significant increase in exam scores in response to written peer-graded exercises completed during class.

Peer-graded, exam-preparation exercises appear to be beneficial, but how good is the peer assessment? That is, how do the scores assigned by students compare to the marks assigned by an expert? To address this question, we implemented a large, randomized, double-blind trial to compare expert and peer grading.

MATERIALS AND METHODS

Course Background

This study involved students in Biology 180, the first in a three-quarter introductory biology sequence designed for undergraduates intending to major in biology or related disciplines. The course enrolled ≈340 students at the time of the study. Most students were sophomores; the content was evolution, Mendelian genetics, diversity of life, and ecology. The course had four 50-min class sessions and a 3-h laboratory each week. Students took two midterms and a comprehensive final exam. All of the exam questions in the course were written—most were short-answer, but some involved labeling or graphing.

Practice Exam Format

Starting in 2005, instructors began requiring a weekly, timed, peer-graded practice exam. The purpose of the exercises was to provide practice answering high-level, exam-style, written questions under time pressure, but in a low-risk environment—meaning that relatively few course points were at stake. The practice exams were meant to complement the use of clickers during class, which provided opportunities for peer interaction and practice with newly introduced concepts based on multiple-choice questions.

During the practice exam exercise, students have 35 min to answer five short-answer questions. After submitting their answers, students are randomly and anonymously given the answers submitted by a different student to grade. Grades have to be submitted within 15 min and are based on a system of 0 (no credit), 1 (partial credit), or 2 (full credit) points per question. For each question, students are given a sample, full-credit answer written by the instructor along with a detailed rubric indicating the criteria for no, partial, or full credit.

Our quarters have 10 wks of instruction; depending on holiday schedules, there are either 9 or 10 practice exams. There are 10 points possible on each weekly practice exam, and the lowest score from the total is dropped—meaning that it is not counted in computing the final grade. Typically, practice exam points represent 11–15% of the total course grade; actual exams total 400 points and represent ≈55% of the final course grade.

In autumn 2005, the class was split into two sections that were taught back-to-back (see Freeman et al., 2007). In this case, students from each section took their practice exams at different times; most of the questions on these exercises were also different.

In most cases the practice exams were implemented with software developed at our university (see Freeman et al., 2007). The software has the advantage of enforcing a timed exercise, with the goal of more accurately reflecting the actual exam environment than an untimed assignment. Questions were intended to test understanding at the upper levels of Bloom's taxonomy (see Crowe et al., 2008) and were meant to be harder than actual exams—although students were under slightly less time pressure during the practice exercise.

It is important to note that the grading system in this course is noncompetitive. Thus, students have no incentive to grade harshly in an attempt to push colleagues into lower bins on a curve.

Example Practice Exam Question, Sample Answer, and Grading Rubric

The following is typical of the types of questions, sample answers, and rubrics presented to students on the practice exams. This practice exam was given just after a class session on speciation that introduced species concepts, allopatric speciation, and sympatric speciation using examples other than apple maggot flies.

Question: Biologists are documenting that a fly species is currently splitting into two distinct species: one has larvae that feed on apple fruits, and the other has larvae that feed on hawthorn fruits. Hawthorns are native to North America, but apples were introduced from Europe <300 years ago. Experiments have shown that adults of each species mate on the type of fruit where egg laying and larval development occur. Why is this observation important, in terms of speciation?

Sample answer: If the two species mate on different fruits, then no gene flow occurs and they are reproductively isolated.

Rubric

• For full credit (2 pts): Clear articulation of logic that mating on different fruits reduces or eliminates gene flow—a prerequisite for speciation to occur.

• Partial credit (1 pt): Missing or muddy logic with respect to connection between location of mating and gene flow, or no explanation of why reductions in gene flow are important.

• No credit (0 pts): both components required for full credit missing; no answer; or answer is unintelligible.

Assessing Student Grading

In the spring quarter of 2005, we divided the class in half, at random, and had one-half of the students do every practice exam online, as individuals, and the other half of the students do the same exercises at the same time in groups of four, as a hard-copy exercise completed in a lecture hall with an instructor (J.W.P.) present. The instructor did not provide the groups with help but distributed the hard-copy exercises, monitored group activity, collected the exercises after 35 min, and randomly assigned a completed exercise to another group for grading. The groups were structured and heterogeneous—they consisted of one student predicted to be in the bottom 25% of the class, two students predicted to be in the middle 50% of the class, and one student predicted to be in the top 25% of the class (see Freeman et al., 2007). After being “binned” in this manner, students were assigned to groups at random.

During this quarter, one of the authors (J.W.P.) chose practice exams completed by individuals at random and graded them. He graded 96 individual exams from the week 5 practice exam and 94 individual exams from the week 10 practice exam (a quarter lasts ≈10 wk). He also graded all 43 of the practice exams graded by groups during week 5 and week 10.

The professional grader was not aware of student identity or the scores assigned by the student graders. In addition, students were not aware that we intended to study how individuals and groups scored relative to a professional grader. The grader was, however, aware of which practice exams had been graded by individuals versus groups. In terms of comparing group versus individual grading, then, the study was designed to be randomized and single-blind.

In the autumn quarter of 2005, we dropped the group exercise to decrease demands on staff time; all students took and graded practice exams individually. The same instructor (J.W.P.) graded 100 randomly chosen practice exams in week 2, 100 randomly chosen practice exams in week 5, and 100 randomly chosen practice exams in week 9. The grader was again blind to student identity and scoring, and students were not aware that we intended to quantify how different their scores were from those assigned by a professional. In terms of comparing grades assigned by individual students versus an expert, then, the study was designed to be randomized and double-blind.

“Blooming” Exam Questions

To assess whether the accuracy of student grading varied with the type of question being asked, one of the authors (S.F.) ranked all of the questions in the study on Bloom's taxonomy of learning, following Crowe et al. (2008). The ranking included a distinction between level 3 (application) questions that represented lower-order cognitive skills versus higher-order cognitive skills. This allowed us to distinguish questions that asked students to apply concepts in new contexts in an algorithmic (“plug-and-chug”) versus nonalgorithmic manner. For example, some practice exam questions asked students to apply the Hardy-Weinberg principle to evaluate observed genotype frequencies. Because students use a standard approach to solve this problem, it is a lower-order level 3 question. We followed Crowe et al. (2008) in considering level 1, 2, and “algorithmic” level 3 questions as testing lower-order cognitive skills, and nonalgorithmic level 3 questions and level 4–6 questions as testing higher-order cognitive skills. In total, there were 29 unique questions in the study. All of the Bloom's rankings were done blind to the student and professional scores.

RESULTS

To assess whether the raw scores were normally distributed, we generated histograms of points assigned for each practice exam by students as individuals, students as groups, or the professional grader (data not shown). Visual inspection of these graphs indicated no obvious or consistent departures from normality. Based on this observation, we used parametric statistics to analyze the data.

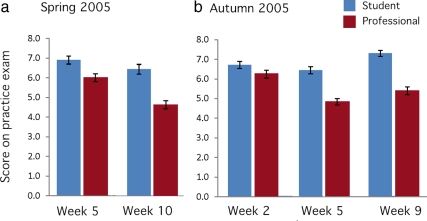
In all five practice exams examined, students were significantly easier graders than the professional. Figure 1 shows the results from exercises graded by individual students versus the professional; Table 1 summarizes the results of paired t tests.

Figure 1.

Students grade practice exams more leniently than a professional. Bars represent mean scores for the practice exam indicated; horizontal lines represent SEs of the mean. Results of statistical tests are reported in Table 1.

Table 1.

Results of paired t tests: Practice exams graded by individual students versus a professional grader

	Mean score: peer grading	Mean score: professional grading	n	t statistic	p value (two-tailed)
Spring 2005: Week 5	6.90 ± 0.20	6.00 ± 0.20	96	−4.95	<<0.0001
Spring 2005: Week 10	6.45 ± 0.25	4.64 ± 0.21	94	−10.43	<<0.0001
Autumn 2005: Week 2	6.71 ± 0.18	6.25 ± 0.20	100	−3.73	0.0003
Autumn 2005: Week 5	6.45 ± 0.18	4.84 ± 0.16	100	−11.45	<<0.0001
Autumn 2005: Week 9	7.3 ± 0.16	5.4 ± 0.20	100	−9.02	<<0.0001

Ten points were possible on each exercise; means are reported with SEs.

To estimate the overall difference in student and professional scores, we used the average difference between student and professional scores on each practice exam to compute a global average. The mean of professionally assigned scores on all of the exercises was 5.43; the mean of student-assigned scores was 6.76. The difference of 1.33 points per 5-question, 10-point exercise represents a 24.5% increase in points awarded to students due to peer versus professional grading. On a per-question basis, however, the increase represents just 0.27 points—roughly a quarter point on each 2-point question. In a term where 9 of the 10-point practice exams contributed to the final grade, the difference would represent an increase of ≈12 points, or typically ≈1.7% of the total points possible.

When all 490 scored exercises in the study are considered together, the correlation between student and professional scoring was high—the Pearson r was 0.61.

To evaluate whether student scoring is more accurate when it was performed by groups rather than individuals, we computed the difference between student and professional scores on the two practice exams evaluated in spring 2005. In each case, we compared the individual-professional difference to the group-professional difference on answers from the same exercise. Unpaired t tests indicate no difference between individual versus group grading, on either exercise evaluated (Table 2).

Table 2.

Results of unpaired t tests: Differences in practice exam scores graded by individual students versus a professional grader and student groups versus a professional grader

	Mean difference: individual students versus professional	Mean difference: student groups versus professional	n for individuals, groups	t statistic	p value (two-tailed)
Spring 2005: Week 5	0.89 ± 0.18	0.76 ± 0.23	96, 43	−0.47	0.64
Spring 2005: Week 10	1.81 ± 0.17	1.38 ± 0.24	94, 43	−1.43	0.15

Means are reported with SEs.

Visual inspection of the data in Figure 1 suggests that the difference between student and professional grading increased late in the term. To test this hypothesis, we computed the difference between each student score and the professional score on the same question for the week 5 and week 10 practice exams in spring 2005 and the week 2, week 5, and week 10 practice exams in autumn 2005. Statistical tests reported in Table 3 confirm that there was significant heterogeneity in the average student-professional difference in each quarter of the study, based on time in the term.

Table 3.

Do differences between student and professional grading vary with time in the term?

a. Spring 2005
	Week 5	Week 10	t statistic	p value (two-tailed)
Mean difference: Individual students versus professional	0.89 ± 0.18 (96)	1.81 ± 0.17 (94)	−3.64	0.0003

b. Autumn 2005
	Week 2	Week 5	Week 10	F value	p value (two-tailed)
Mean difference: individual students versus professional	0.46 ± 0.12 (100)	1.61 ± 0.14 (100)	1.9 ± 0.21 (100)	21.93	<<0.0001

Means are reported with SEs; sample sizes (numbers of practice exams graded) are in parentheses; the results are based on an unpaired t test in part (a) and an ANOVA in part (b).

Several patterns emerged when we analyzed the Bloom's taxonomy rankings of the 29 questions in the study. The average Bloom's level was 3.0 ± 0.19, which supports the original intent of focusing the exercises on higher-order cognitive skills. As expected from previous reports in the literature, questions that tested higher-order cognitive skills were more difficult for students. Using the professional grader's scores on all answers, we found a mean of 1.32 ± 0.03 out of 2 points possible for questions that tested lower-order thinking (n = 688 responses) versus a mean of 1.00 ± 0.02 for questions that tested higher-order thinking (n = 1760 responses; t = 9.5, p ≪ 0.001).

The student-professional accuracy gap in grading was also much wider for questions that tested higher-order versus lower-order thinking (Table 4). An ANOVA based on the six levels of Bloom's taxonomy also indicated highly significant heterogeneity in means (data not shown). Finally, in autumn 2005 there was a significant difference in the average Bloom's level based on time in the term (Table 5)—in both quarters, practice exam exercises late in the quarter tended to include more high-level questions.

Table 4.

Differences between student and professional grading vary with level on Bloom's taxonomy

	Lower-order cognitive skills	Higher-order cognitive skills	t statistic	p value (two-tailed)
Mean difference: individual students versus professional	0.15 ± 0.02 (688)	0.31 ± 0.02 (1760)	−5.96	<<0.0001

Means are reported with SEs; sample sizes (number of student answers) are in parentheses; the t statistic is from an unpaired test. For a definition of lower-order and higher-order thinking skills, see Methods.

Table 5.

Relationship between time-in-term and average Bloom's level of practice exam questions

a. Spring 2005
	Week 5	Week 10	t statistic	p value (two-tailed)
Average Bloom's level	2.6 ± 0.40 (5)	3.2 ± 0.66 (5)	−0.77	0.46

b. Autumn 2005
	Week 2	Week 5	Week 10	F value	p value (two-tailed)
Average Bloom's level	2.8 ± 0.13 (10)	2.8 ± 0.37 (5)	4.0 ± 0.33 (10)	6.6	0.006

Means are reported with SEs; sample sizes (number of different questions asked) are in parentheses.

DISCUSSION

Is student grading good enough to use? This question is subjective and context-dependent; in our case, the answer is yes. One key observation is that our practice exams were more difficult than the actual exams. Midterms and finals in this course typically have means ranging from 65–72%, but the professionally graded mean on practice exams was only 54.3%. The increase in points due to student grading, to a mean of 67.6%, helped accomplish our goal of administering practice exams that would roughly match scores on actual exams, and thus not deflate or inflate final grades.

Overall, the quality of student grading reported here appears to be typical. A meta-analysis of 48 studies that evaluated differences between peer grading and professional grading on identical assessments in college courses reported an average correlation of 0.69 (Falchikov and Goldfinch, 2000)—similar to the correlation reported here.

Are students almost always easier graders than professionals? Based on work done to date, it is difficult to identify any systematic trends in how students and professionals differ in their grading. English et al. (2006), for example, report that medical students grade written assignments more harshly than expert tutors. Evans et al. (2007) show that dental students assign scores that are indistinguishable from professional scores when they evaluate tooth-extraction procedures completed by students; similarly, Walvoord et al. (2008) find no difference between scores assigned by students and a professional on written assignments in an introductory biology class. In contrast, Paré and Joordens (2008) find that students graded more leniently than graduate students on written assignments in an introductory psychology class; van Hattum-Janssen et al. (2004) determined that students graded exam-type assessments in an introductory engineering course more generously than a professional; and data in Hafner and Hafner (2003) show that students gave higher grades than professionals on oral presentations in a college biology class. The field is young, though, and stronger patterns may emerge as additional data accumulate.

To date, it is also not clear whether the accuracy of student grading can improve with experience and/or training. Allain et al. (2006) and Gehringer (2001) advocate “grading the graders” to guard against low effort, but there are little if any data on techniques that might improve the accuracy of peer grading.

Conclusions about the accuracy of grading by student groups versus students as individuals appear more robust. In their meta-analysis, Falchikov and Goldfinch (2000) assessed correlations between student and professional scores when students worked in various sized groups, and concluded that scoring by groups was just as reliable as scoring by individuals. The same result is reported here, suggesting that group grading has no apparent advantage over individual grading, at least in terms of accuracy.

If introductory biology instructors find the student-professional gap documented here acceptable, it may encourage them to add peer-graded written exercises to courses that currently rely exclusively on multiple-choice exams. This may be particularly important when traditional assessments rarely ask questions that test higher-order thinking, or in programs where students will be asked to write exam answers in subsequent, upper-division courses.

The observation that the student-professional difference increased for questions that demand higher-order cognitive skills deserves comment. Although many studies have shown that student performance declines on assessment questions at higher levels of Bloom's taxonomy (e.g., Crowe et al., 2008), this study may be the first to show the same pattern in student grading. Students not only have trouble answering high-level application, analysis, synthesis, and evaluation questions, they also have trouble grading them. This pattern probably explains why the student-professional gap increased late in the quarters we studied—we unconsciously, but clearly (in autumn of 2005), asked higher-level questions later in the term.

Finally, this study was focused on evaluating peer grading as a practical means of enforcing regular practice with exam-style questions. As a result, it did not address the question of whether students learn from the grading process itself. This important issue deserves to be addressed in future work. One possible experimental design would be based on having different students grade different suites of practice questions. If the act of grading is beneficial, then performance on subsequent exam questions should be better if the concept or skill being assessed conforms to one where students had functioned as a grader. In addition, it would be interesting to require comments by student and professional graders on each question. Are the comments on higher-order questions—where a particularly large professional-student accuracy gap exists—substantively different? And does the act of commenting help with meta-cognition and subsequent performance, as hypothesized for peer review of essays? Exploring peer grading as a technique to enhance student learning should be a fruitful area for further research.