Figure 4. Zipf's law and Heaps' law in four example systems.

(a) Words in Dante Alghieri's great book “La Divina Commedia” in Italian [44] where is the frequency of the word ranked and is the number of distinct words. (b) Keywords of articles published in the Proceedings of the National Academy of Sciences of the United States of America (PNAS) [30] where is the frequency of the keyword ranked and 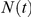is the number of distinct keywords; (c) Confirmed cases of the novel virus influenza A (H1N1) [45] where 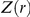is the number of confirmed cases of the country ranked and is the number of infected country in the presence of confirmed cases over the world; (d) PNAS articles having been cited at least once from 1915 to 2009 where is the number of citations of the article ranked and is the number of distinct articles in the presence of citations to PNAS. In (c), the data set is small and thus the effective number is only two digits. The fittings in (c1) and (c2) only cover the area marked by blue. In (d1), the deviation from a power law is observed in the head and tail, and thus the fitting only covers the blue area. The Zipf's (power-law) exponents and Heaps' exponents are obtained by using the maximum likelihood estimation [3], [43] and least square method, respectively. Statistics of these data sets can be found in Table 1 (the data set numbers of (a), (b), (c) and (d) are 9, 10, 34 and 35 in Table 1) with detailed description in Materials and Methods .