Table 1. Empirical statistics and analysis results of real data sets.
| No. |

|
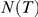
|

|

|

|

|
| 1 | 206779 | 18217 | 1.323 | 0.756 | 0.725 | 0.738 |
| 2 | 20516 | 5671 | 0.969 | 1 | 0.858 | 0.859 |
| 3 | 109854 | 13906 | 1.063 | 0.941 | 0.845 | 0.817 |
| 4 | 449205 | 20220 | 1.464 | 0.683 | 0.667 | 0.679 |
| 5 | 68458 | 9191 | 1.095 | 0.913 | 0.823 | 0.810 |
| 6 | 81037 | 13254 | 1.025 | 0.976 | 0.859 | 0.832 |
| 7 | 63742 | 16622 | 1.057 | 0.946 | 0.840 | 0.852 |
| 8 | 138985 | 15550 | 1.188 | 0.842 | 0.787 | 0.765 |
| 9 | 101940 | 12667 | 1.117 | 0.895 | 0.818 | 0.799 |
| 10 | 504610 | 116800 | 0.893 | 1 | 0.936 | 0.863 |
| 11 | 53214 | 34194 | 0.540 | 1 | 0.983 | 0.946 |
| 12 | 310853 | 69185 | 0.939 | 1 | 0.913 | 0.871 |
| 13 | 30852 | 17562 | 0.595 | 1 | 0.972 | 0.939 |
| 14 | 2761 | 2328 | 0.397 | 1 | 0.964 | 0.978 |
| 15 | 58300 | 22599 | 0.786 | 1 | 0.941 | 0.914 |
| 16 | 20660 | 8155 | 0.790 | 1 | 0.921 | 0.890 |
| 17 | 226090 | 69251 | 0.692 | 1 | 0.977 | 0.894 |
| 18 | 176291 | 62567 | 0.572 | 1 | 0.989 | 0.920 |
| 19 | 44735 | 19933 | 0.685 | 1 | 0.961 | 0.915 |
| 20 | 1924 | 1323 | 0.463 | 1 | 0.946 | 0.939 |
| 21 | 5093 | 2985 | 0.593 | 1 | 0.941 | 0.920 |
| 22 | 3490 | 2442 | 0.500 | 1 | 0.952 | 0.950 |
| 23 | 1403 | 787 | 0.524 | 1 | 0.926 | 0.931 |
| 24 | 7469 | 4142 | 0.654 | 1 | 0.936 | 0.925 |
| 25 | 7710 | 3857 | 0.658 | 1 | 0.935 | 0.930 |
| 26 | 3232 | 2658 | 0.416 | 1 | 0.964 | 0.976 |
| 27 | 13165 | 7743 | 0.612 | 1 | 0.959 | 0.936 |
| 28 | 3749 | 2353 | 0.568 | 1 | 0.943 | 0.940 |
| 29 | 30092 | 11002 | 0.815 | 1 | 0.924 | 0.891 |
| 30 | 21894 | 8666 | 0.776 | 1 | 0.930 | 0.900 |
| 31 | 7627 | 3841 | 0.685 | 1 | 0.933 | 0.930 |
| 32 | 4185 | 2242 | 0.675 | 1 | 0.921 | 0.929 |
| 33 | 23822 | 10753 | 0.648 | 1 | 0.959 | 0.917 |
| 34 | 8829 | 40 | 3.0 | 0.33 | 0.34 | 0.35 |
| 35 | 237982 | 56961 | 0.462 | 1 | 0.993 | 0.929 |
 is the total number of elements,
is the total number of elements, 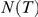 is the total number of distinct elements,
is the total number of distinct elements,  is the Zipf's exponent obtained by the maximum likelihood estimation
[3], [43],
is the Zipf's exponent obtained by the maximum likelihood estimation
[3], [43],  is the asymptotic solution of the Heaps' exponent as shown in Eq. 7,
is the asymptotic solution of the Heaps' exponent as shown in Eq. 7,  is the numerical value of the Heaps' exponent given
is the numerical value of the Heaps' exponent given 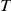 and
and  as shown in Fig. 3, and
as shown in Fig. 3, and  is the empirical result of the Heaps' exponent obtained by the least square method. The effective number of the 34th data set is only two digits since the size of this data set is very small. Except the 4th data set, in all other 34 real data sets, the numerical results based on Eq. 6 outperform the asymptotic solution shown in Eq. 7. Detailed description of these data sets can be found in
Materials and Methods
.
is the empirical result of the Heaps' exponent obtained by the least square method. The effective number of the 34th data set is only two digits since the size of this data set is very small. Except the 4th data set, in all other 34 real data sets, the numerical results based on Eq. 6 outperform the asymptotic solution shown in Eq. 7. Detailed description of these data sets can be found in
Materials and Methods
.
