Recursions for statistical multiple alignment

Abstract

Algorithms are presented that allow the calculation of the probability of a set of sequences related by a binary tree that have evolved according to the Thorne–Kishino–Felsenstein model for a fixed set of parameters. The algorithms are based on a Markov chain generating sequences and their alignment at nodes in a tree. Depending on whether the complete realization of this Markov chain is decomposed into the first transition and the rest of the realization or the last transition and the first part of the realization, two kinds of recursions are obtained that are computationally similar but probabilistically different. The running time of the algorithms is 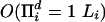, where L_i is the length of the ith observed sequences and d is the number of sequences. An alternative recursion is also formulated that uses only a Markov chain involving the inner nodes of a tree.

Proteins and DNA sequences evolve predominantly by substitutions, insertions, and deletions of single letters or strings of these elements, where a letter is either a nucleotide or an amino acid. During the last two decades, the analysis of the substitution process has improved considerably and has been based increasingly on stochastic models. The process of insertions and deletions has not received the same attention and is presently being analyzed by optimization techniques, for instance maximizing a similarity score as first used by Needleman and Wunsch (1).

Thorne, Kishino, and Felsenstein (2) proposed a well defined time-reversible Markov model for insertions and deletions [denoted more briefly as the Thorne, Kishiro, and Felsenstein (TKF) model] that allowed a proper statistical analysis for two sequences. Such an analysis can be used to provide maximum likelihood sequence alignments for pairs of sequences or to estimate the evolutionary distance between two sequences. Recently, an algorithm was presented by Steel and Hein (3) that allows statistical alignment of sequences related by a star-shaped tree, a tree with one inner node. Hein (4) formulated an algorithm that calculates the probability of observing a set of sequences related by a given tree in time O((Π_i L_i)²), where L_i is the length of the ith sequence. This is also the time required by Steel and Hein's algorithm (3). Holmes and Bruno (5) used the algorithm by Hein (4) to design a Gibbs sampler that has the potential of analyzing a higher number of sequences than the exact algorithms. The present work accelerates, extends, and formalizes the algorithm in ref. 4. In particular, the time requirement for the algorithm presented here is reduced to O(Π_i L_i).

The TKF model is formulated in terms of links and associated letters. To each link is associated a letter that undergoes changes, independently of other letters, according to a reversible substitution process (identical to the site-substitution process, where insertions and deletions are not allowed). A link and its associated letter are deleted after an exponentially distributed waiting time with mean 1/μ. While a link is present, it gives rise to new links at the rate λ. A new link is placed immediately to the right of the link from which it originated, and the associated letter is chosen from the stationary distribution of the substitution process. At the left of the sequence is a so-called immortal link that never dies and gives rise to new links at the rate λ, preventing the process from becoming extinct.

For the TKF model on a tree, the defining parameters are the death rate μ and the birth rate λ, as described above, together with a time parameter τ for each edge of the tree. The time parameter τ defines how long the process runs along a given edge. When the process splits into two subprocesses at an inner node, the two subprocesses are independent.

The main probabilistic aspects of the TKF model are given by Eqs. 2–4 and 8 below. The structure of probabilities 3 and 4 allows us to write the joint probability of observed sequences at the leaves of a tree together with the alignment and the unobserved sequences at inner nodes of the tree as a Markov chain along the sequences observed, until the process reaches an absorbing state. The process of observed sequences therefore becomes a hidden Markov chain. Having obtained this identification, we can use traditional methods for obtaining a recursion for the calculation of the probability of the observed sequences. In particular, we state two recursions, one corresponding to splitting the process according to the first state of the Markov chain, and the other corresponding to splitting the process according to the last state of the Markov chain. In Approach 1, a state of the hidden Markov chain describes an element in the alignment for the whole tree, which gives a recursion with time complexity O(Π_i L_i) when implemented using dynamic programming. In Approach 2, we take a state of the hidden Markov chain to be an element in the alignment of the tree consisting of inner nodes only. This gives a recursion with time complexity O((Π L ² i i)); however, this can be reduced to O(Π_i L_i), and actually we obtain a recursion with slightly fewer terms than that considered in Approach 1.Westartin Preliminaries by defining the states of our hidden Markov chain and finding the transition probabilities of the Markov chain. This section introduces necessary notation to allow for a precise mathematical formulation.

Preliminaries

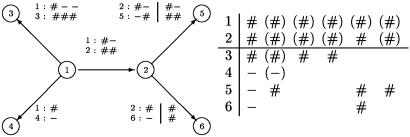
Notation. We consider a tree with d′ inner nodes and d leaves. The inner nodes are numbered from 1 to d′, with 1 being the root and where the ancestor a(i) of i is to be found in {1, 2,..., i – 1}. The leaves are numbered from d′ + 1 to d′ + d, with the descendants of inner node i being numbered before the descendants of inner node j for j > i. For a tree with two inner nodes and four leaves, the numbering can be seen in Fig. 1.

Fig. 1.

A tree with four leaves, where the link a root 1 survives at inner node 2 and produces a new link at leaf 2.

The evolutionary time distance from the ancestor a(z) of a node z to the node z is τ(z). The observed sequences are S_j for j = d′ + 1,..., d′ + d, where S_j is the observed sequence at the leaf j. The length of S_j is L_j, and the ath entry of S_j is denoted S_j(a). We write S_j(a: b) for entries from a to b with a and b included. We let S denote the collection of sequences, and for two d-dimensional vectors u, v indexed by j = d′+ 1,..., d′+ d and with integer entries S(u: v) denote the collection of subsequences S_j(u_j: v_j). To compare two d-dimensional vectors u, v, the notation

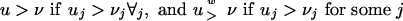is used, with similar definitions for other relations. To shorten the formulae, we write for two vectors, K, l, with l ≥ 0, S[K, l] = S((K – l + 1): K). Finally, L is the vector with entries L_j.

The notation 1(E) is used for the function that is 1 when the expression E is true and 0 otherwise. We use the symbol # for a link, and when following the fate of a link along the tree, we write # at node i if the link is present, and we write – at node i if the link died along the edge from a(i) to i.

Markov Structure of the TKF Model for Two Sequences. In this subsection, the TKF model from time zero to time τ is considered. We rewrite the probabilities for the deletion of a link and for the number of new links that appear before time τ in such a way that we recognize a Markov structure along the sequences with states

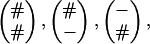[1]

corresponding to survival of the link, deletion of the link, and insertion of a new link.

Let V = 1 if the link survives, and let V = 0 if the link dies. Because the death rate is μ, we have

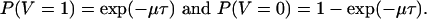[2]

Let N be the number of new links after time τ. From Thorne, Kishino, and Felsenstein (2), we have

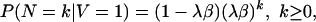[3]

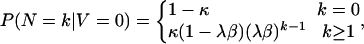[4]

where

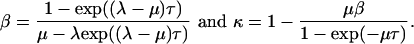From these formulae, we find

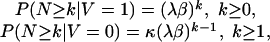and this implies

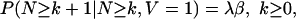[5]

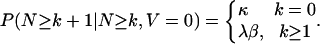[6]

The important point for establishing a Markov structure along the sequences is that Eqs. 5 and 6 are equal and independent of k for k ≥ 1. The independence of k gives the Markov structure for the number of new links, that is, a new link is added with probability λβ, and we stop adding new links with probability 1 – λβ. We can thus generate V and N by a Markov chain with transition probabilities

[7]

To interpret the whole alignment as a Markov chain, we note that the number K of links at stationarity has the following distribution. (see Thorne, Kishino, and Felsenstein, ref. 2),

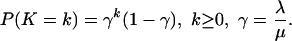[8]

Again this corresponds to a Markov chain where we add a link with probability γ, and we stop adding more links with probability 1 – γ. Having reached the stop state in system 7, we thus add a new link at time zero with probability γ and start a new round of the Markov chain in Eq. 7. We can combine this into a Markov chain on the states in Eq. 1 together with an End state as follows:

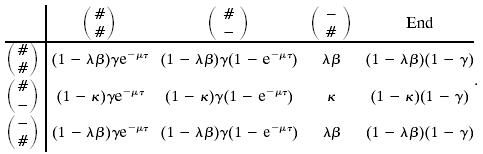[9]

As an example, the (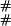),()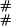 entry corresponds to going to the stop in Eq. 7 from (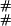), adding a link at time zero with probability γ, and going to (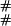), from start in Eq. 7.

When considering the TKF model on a tree, we will need the terms in Eq. 7 for each edge of the tree. Because we number the edges by the node at the end of the edge, we introduce for each node j > 1 the terms

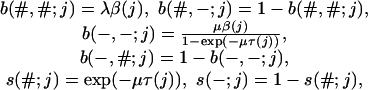where β(j) = {1 - exp((λ - μ)τ(j))}/{μ - λ exp((λ - μ)τ(j))}.

States. Because the probability of an alignment on the tree is the product of the probabilities of the pairwise alignments along the edges, we can use the hidden Markov structure presented in Markov Structure of the TKF Model for Two Sequences for pairwise alignment to obtain the hidden Markov structure for alignment on the tree. To obtain this, we need to choose states for the hidden Markov model on the tree that allow us to identify the states of the hidden Markov model for the pairwise alignments along the edges.

When translating a set of pairwise alignments between the nodes (a(j), j), 2 ≤ j ≤ (d + d′) into a sequence of states for the multiple alignment, we will use the convention that if a birth at node i and a birth at node j > i both are the result of a birth at node z < i, then the birth at node j will appear before the birth at node i in the sequence.

A state represents two things, a new event in part of the tree and a “history” in the complementary part of the tree. The two together give information on which new events are possible in the next state. Astate ξ consists of some subsets of nodes together with a value ξ(z) ∈ {#, –} for the nodes z in these subsets. The new event attached toastate ξ is a birth of a link at some node t(ξ) and, if t(ξ) is an inner node, the survival (ξ(z) = #) or nonsurvival (ξ(z) = –) along the tree down from t(ξ). We let T(ξ), respectively L(ξ), be the set of inner nodes z > t(ξ), respectively leaves, where we have survival or where the link died on the edge leading to the node. The history corresponds to a birth at node 1 and the survival (ξ(z) = #) or nonsurvival (ξ(z) =–) along inner nodes z < t(ξ), with the property that the link survived at the ancestor a(t(ξ)). We let H(ξ) be the set of inner nodes z < t(ξ) where the link survived or died on the edge leading to the node. Furthermore, if t(ξ) is a leaf, the history contains an inner node h(ξ) < a(t(ξ)), h(ξ) ∈ H(ξ) with ξ(h(ξ)) = # and a set HL(ξ) of leaves z > t(ξ) being descendant of h(ξ) and for which the link at h(ξ) survived or died on the edge leading to the leaf. For a state where t(ξ) is an inner node, the next state can have a birth of a new link in any of the nodes in H(ξ) ∪ {t(ξ)} ∪ T(ξ) ∪ L(ξ), and for a state with t(ξ) a leaf, a new link can be born at the nodes in H(ξ) ∪ HL(ξ) ∪ {t(ξ)}. Note that the history is defined in such a way as to respect our convention of the ordering of the births.

To exemplify the definitions above, let us consider the tree in Fig. 1 with two inner nodes. We represent the states as six-dimensional columns with values # or – in {t(ξ)} ∪ T(ξ) ∪ L(ξ), with values (#) or (–)in H(ξ) ∪ HL(ξ), and with no value in the remaining nodes. All 45 possible states are listed in Table 1. Column 1 of Table 1 gives the 16 states corresponding to a birth at node 1 that survived at inner node 2. That the birth is at node 1 leaves no room for a history. Column 4 gives the two states corresponding to a birth at leaf 4 with H(ξ) = {1, 2}, h(ξ) = 1, and HL(ξ) = {3}. There are no values at leaves 5 and 6 due to our convention of the ordering of the births. Column 9 gives the four states corresponding to a birth at inner node 2. Here there are no values at leaves 3 and 4 due to our convention. In Fig. 1, the translation between the set of pairwise alignments and the states of the multiple alignment is illustrated. Fig. 1 displays the situation where there is one link only at node 1. This link survives at inner node 2 and produces a new link at node 2. The original link does not survive at leaves 4–6, but produces a new link at leaf 5. The original link survives at leaf 3 and produces two new links at this leaf. The new link at inner node 2 survives in both leaves 5 and 6 and produces a new link at leaf 5. The set of states in the multiple alignment is shown in Fig. 1 Right. The first state is the birth of the link at node 1 together with the survival and nonsurvival of this link. State 2 is the birth at node 5 coming from the original link at node 1. States 3 and 4 are the two births at node 3. State 5 is the birth of a new link at node 2 together with the survival at nodes 5 and 6. Note that there are no values in this state at nodes 3 and 4 due to the convention that a birth at inner node 2 implies that all births at nodes 3 and 4 have been handled. Finally, the last state is the birth at node 5 originating from the new link at node 2.

Table 1.

States of the Markov chain for the tree in Fig. 1

	Column number
Node	1	2	3	4	5	6	7	8	9	10	11
1	#	(#)	(#)	(#)	(#)	#	(#)	(#)	(#)	(#)	(#)
2	#	(#)	(#)	(#)	(#)	-	(-)	(-)	#	(#)	(#)
3	a3	(a3)	(a3)	(a3)	#	a3	(a3)	#
4	a4	(a4)	(a4)	#		a4	#
5	a5	(a5)	#						a5	(a5)	#
6	a6	#							a6	#
	16	8	4	2	1	4	2	1	4	2	1

Any of the variables a_i can be either # or -. The last row gives the number of states of the indicated form.

As mentioned in the beginning of this subsection, we get a Markov chain because we can identify all the pairwise alignments along the edges from the states we use. To illustrate this, let us write down the probability of the alignments in Fig. 1 as follows:

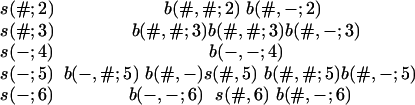[10]

Here each row represents the probability of the alignment along one of the edges. The terms in a row have been spread out to align terms vertically, as explained below. The terms s(#; j) and s(–; j) are the two entries in the first row of Eq. 7 corresponding to survival and nonsurvival of a link along the edge leading to node j, b(#, #; j), b(#, –; j) are the two entries from the second and fourth row of Eq. 7, and b(–, #; j) and b(–, –; j) are the two entries from the third row of Eq. 7. The first row of Eq. 10 gives the probability of the alignment between nodes 1 and 2, which is given through the survival of the link together with the probability of a birth of a new link and the probability of no further links. The product of the terms in each column in Eq. 10 represents a transition probability in the chain with 45 states, except for the first column that has to be combined with the probability related to leaving a previous state, and the last column that has to be combined with the probability related to the next link at root 1. As can be seen, each column is a function of the corresponding consecutive set of states in Fig. 1.

When stating the transition probabilities, it is convenient to have the following notation. For a state ξ, we let γ = γ(r, ξ) be the state we enter when having a birth at the leaf r. If t(ξ) is an inner node r ∈ L(ξ), H(γ) = H(ξ) ∪ {t(ξ)} ∪ T(ξ), h(γ) = t(ξ), HL(γ) = {z ∈ L(ξ)|z < r}, and γ(z) = ξ(z) for nodes in these sets. If t(ξ) is a leaf r ∈ HL(ξ) ∪ {t(ξ)}, H(γ) = H(ξ), h(γ) = h(ξ), HL(γ) = {z ∈ HL(ξ)|z < r}, and γ(z) = ξ(z) for nodes in these sets. The set of all states is denoted Ξ, and the subset of states ξ with t(ξ) an inner node is denoted Ξ₁.

Transition Probabilities. A transition probability p(x, y) of going from state x to state y can be written formally as p(x, y) = stop · new · survival, where stop gives the probability of no new links at certain nodes, new gives the probability of a new link at a particular node, and survival gives the probability of the fate of the new link. We thus find for a state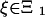

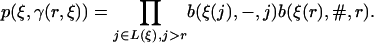[11]

For a state ξ with t(ξ) a leaf, we get with s = t(ξ)

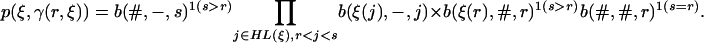[12]

For two states ξ, η ∈ Ξ₁, a transition from ξ to η is possible only if η corresponds to a new link at one of the inner nodes from which ξ allows the introduction of new links. This can be formulated formally as

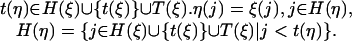In this case, the transition probability is

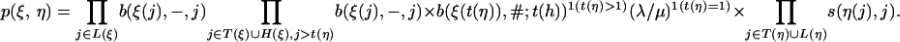[13]

When t(ξ) is a leaf and t(η) is an inner node, the transition from ξ to η requires

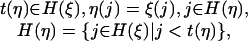and the transition probability p(ξ, η) is

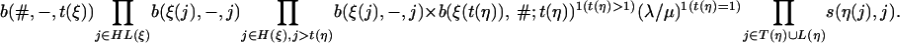[14]

For a transition to the end state, only the first line of Eqs. 13 and 14 should be used, multiplied by (1 – λ/μ), and with t(η) = 1. Finally, the transition probabilities from the immortal state I can be calculated as if I corresponds to the state ξ₀ with a new link at node 1 that survives in all of the tree.

Algorithms

In this section, we present two algorithms for computing the probability of the observed sequences S_j, for j = d′ + 1,..., d′ + d, being related by the given evolutionary tree. Both algorithms are based on the hidden Markov chain described in the previous section but differ in their choice of states. In the first algorithm, the states describe the alignment for both inner nodes and leaves. The running time is 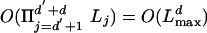, where L_max is the maximum length of the observed sequences. In the second algorithm, the states describe the alignment for inner nodes only. The running time is now 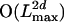, but the algorithm can be rewritten to obtain an 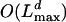running time as in the first approach. The principle for deriving the algorithms is classical and very well known: we consider what happens in either the first or last step of the Markov chain.

Approach 1: Inner Nodes and Leaves. Notation. We consider a Markov process x₀, x₁,..., x_N that starts in the initial state I and stops at a random time N + 1 in the end state E. Thus x₀ = I, x_i ∈ Ξ, for i = 1,..., N, and x_N+1 = E. The transition probability going from x to y is p(x, y) as described in Transition Probabilities. A state ξ ∈ Ξ₁, corresponding to the birth of a link at an inner node, emits a letter in those observed sequences S_z for which z ∈ L₁(ξ) = {u ∈ L(ξ)|ξ(u) = #}. A state ξ ∉ Ξ₁ emits a letter in the sequence S_t(ξ) only. For any state x ∈ Ξ, we let

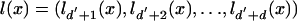[15]

be a vector indexed by the numbering of the observed sequences and consisting of ones in those coordinates for which x emits a letter and zeroes in the other coordinates:

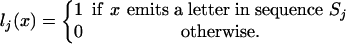[16]

For the state x_i in the hidden Markov chain, we use the shorthand notation lⁱ for the vector l(x_i). The lengths Lⁱ of the sequences emitted by the first i states x₁,..., x_i can then be written as 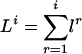. With this notation, the state x_i emits the letters 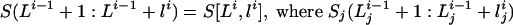is the empty set if lⁱ_j = 0. The probability that a state x emits the vector of letters s (with the possibility that some of the coordinates of s are equal to the empty set) is p_e(s|x).

Backward recursion. For an arbitrary vector K ≥ 0 and state x₀ ∈ Ξ, we define F(K|x₀) = P(S(K + 1: L)|x₀), that is, the probability that the sequences S((K + 1): L) are produced by a set of states x₁, x₂,... given that the Markov chain starts in the state x₀. Clearly, P(S(1: L)|x₀ = I) = F(0|I). Summing over the states of the Markov chain F(K|x₀) is given by

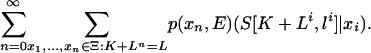[17]

When K <^w L and K ≤ L, the recursion for F(K|x₀), with 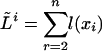, is

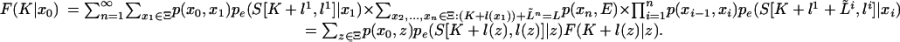[18]

When K = L, the recursion is

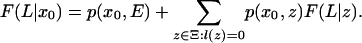[19]

Recursion 18 states that the probability of the sequences S((K + 1): L) produced by states x₁, x₂,..., given that we start in state x₀, is a sum over the possible states of x₁. Each term in the sum is the product of the transition probability of going from x₀ to x₁, the emission probability for those letters emitted by x₁, and the probability of the remaining sequences S((K + l(x₁) + 1): L) given that we start in x₁. If in recursion 18 we replace the summation by the max operation, we obtain a recursion for finding the alignment with the highest probability. This is known as the Viterbi algorithm in the hidden Markov model literature.

Hein, Jensen, and Pedersen (6) also derive a forward recursion by separating out the contribution from x_n instead of x₀. Computationally, there is no difference between the forward and backward recursions. However, the latter has an interpretation as a probability, thereby making it easier to understand.

Emission probabilities. For a full description of the TKF model, we need a model for the substitution process. We let 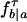be the probability for the substitution of a letter a by b over a time period τ. The stationary probabilities for this transition matrix are denoted by π.

When a state corresponds to a birth of a new link in one of the leaves only, that is, t(ξ) is a leaf, the emitted vector s has a letter at the node t(ξ) only, and the emission probability is simply the stationary probability π(s(t(ξ))). For a state ξ ∈ Ξ₁ corresponding to a birth of a new link at inner node t(ξ), the emitted vector s has letters at those nodes z ∈ L(ξ) for which ξ(z) = #. With a(j), the ancestor of a node j, and with

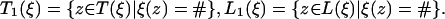[20]

we can write the emission probability as

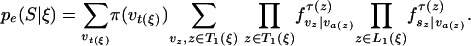[21]

This formula simply says that the probability of the emitted letters s_z, z ∈ L₁(ξ) is the sum of the joint probability of the ancestral and emitted letters over the possible values of the ancestral letters. Implementation and analysis. Let us briefly discuss how to implement the recursion given by Eqs. 18 and 19. There is a complication, in that there will always be terms on the right-hand side of the equations for which K + l(z) = K or l(z) = 0. The states ξ ∈ Ξ₁ for which l(ξ) = 0 are characterized by having ξ(z) =– for all z ∈ L(ξ), that is, the new link does not survive at any of the leaves. Let us denote this class of states by C. Imagine that for some K, the term F(K̃|x) has been calculated for all K̃ >^w K, K̃ ≥ K and all x ∈ Ξ. For each x ∈ C, recursion 18 gives

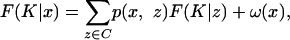[22]

with ω(x) known. Let Q be the matrix with entries p(z₁, z₂), z₁, z₂ ∈ C. Then, because the entries are nonnegative and the sum along a row is < 1, the matrix I_C – Q, where I_C is the identity matrix, is invertible, and the set of linear equations 22 has a unique solution. Having solved this system of equations, we can next calculate F(K|x) for x ∉ C directly from Eq. 18, or from Eq. 19 when K = L. Also in the case of the Viterbi algorithm for finding the alignment with the highest probability, we must, for a given K in the recursion, first solve for the states in C. The boundary conditions for the recursion are F(K|x) = 0 when K >^w L.

To run the algorithm, we need to calculate F(K|x) for any K ≤ L and for any x ∈ Ξ. The number of steps needed is therefore of the order N Π^d_i=1 L_i, where N is the number of elements in the set Ξ.

For illustration purposes, we have implemented recursion 18 as well as the Viterbi algorithm and an algorithm for simulating alignments conditional on the observed sequences for the case of four observed sequences. No attempt to optimize the program has been made, and the program therefore runs only on short sequences. As an example, we use a set of simulated sequences kindly supplied by Yun Song (Oxford University, Oxford). The parameters used in the simulation are λ = 0.05, μ = 0.052, and the Jukes–Cantor model for substitution where the rate of leaving a state is 0.3. All edges of the tree have lengths 1. We use the same parameters when finding the maximal alignment. The true alignment that generated the sequences and the maximal alignment can be seen in Table 2. We have also included an alignment obtained from the clustal w program by Higgins, Thompson, and Gibson (7). The total probability of the observed sequences is 7.62 × 10^–41, as obtained from recursion 18, and the probability of the maximal alignment is 2.04 × 10^–43, contributing only 0.27% to the total probability.

Table 2. Example of alignment.

True	Maximal	clustal w
TTATAT-G-ACTTG-CC-GG	T-TATA-TGACTTGCCGG	TTATAT--GAC-TTGC-CGG
CT-TCG-G-ACGTG-GC-TC	C-T-TC-GGACGTGGCTC	CT-T-C-GGACGTGGCTC--
CCAAAC-GGACGTTAC--GC	CCAAAC-GGACGTTACGC	CCAAAC-GGACGTTACGC
-AAAACAG-GACTTAT-A-C	A-AAACAGGAC-TTATAC	-AAAACAGGAC-TTATAC--

Four sequences and their true alignment that generated the sequences, the maximal alignment obtained from the Viterbi algorithm, and the alignment obtained from the CLUSTAL W program (www.ebi.ac.uk/clustalw).

The maximal alignment and the clustal w alignment agree on aligning GAC in the middle. We have run 500 simulations of the conditional alignment given the observed sequences, and in 78% of the cases, we find that GAC is aligned. clustal w aligns the last C of the four sequences, and this is not seen in the maximal alignment. In the 500 simulations from the conditional alignments, we never encountered a case where the last C was aligned. Generally, the possibility of simulating alignments from the conditional distribution given the observed sequences allows us to make statements on the reliability of features seen in an alignment.

Approach 2: Inner Nodes Only. Notation. In Approach 1, a state described a column of the alignment for all of the inner nodes and leaves, and a state emitted at most one letter in each of the observed sequences. In this section, we will instead let the states describe the inner nodes only, which in turn necessitates the emission of arbitrary long subsequences among the observed sequences. This implies an extra sum in the recursion, thus seemingly making the recursion more complicated. However, we can rewrite the recursion, ending up with a recursion of the same complexity as before and with fewer terms than in Approach 1.

More precisely, a state ξ is a birth of a new link at an inner node and is characterized by the node t(ξ) at which the link is born; the set T(ξ) of inner nodes describes the fate of the link, and the set H(ξ) gives the history of the new link. As before, L(ξ) is the set of leaves descending from t(ξ) or from the nodes in T₁(ξ) (see Eq. 20). As in Eq. 15, l(x) denotes the lengths of the emitted subsequences. Contrary to Eq. 16, l(x) is no longer determined by the state x; the state determines only at which nodes it is possible to emit letters:

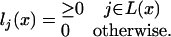[23]

We again use lⁱ = l(x_i), furthermore take l⁰ ≥ 0 to be the length of the subsequence emitted by the immortal link, and define 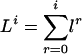to be the lengths of the sequences emitted by the first i states. The emission probability q_e(K, l|x) is now both the probability of emitting subsequences of length l_j, j = d′ + 1,..., d′ + d and the probability that the emitted letters are S_j((K_j – l_j + 1): K_j). To state this probability, we define

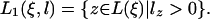In the formula below, u denotes the subset of the leaves L₁(ξ, l) at which the link survives from the ancestral inner nodes. To shorten the formula, we define q(#; z) = s(–; z)b(–, #; z), q(–; z) = s(–; z)b(–, –; z), 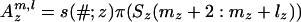, and 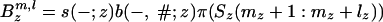, where π(S_j(a: b)) = Π^b_i=a π(S_j(i)). Then the probability that the state ξ emits the subsequences S(m + 1: m + l) is q_e(m + l, l|ξ), given by

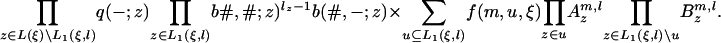[24]

The function f(m, u, ξ) is the emission probability for the first letter at those leaves where we have survival of the link and is given by p_e(s|ξ) from Eq. 21, with L₁(ξ) replaced by u and s_z replaced by S_z(m_z + 1). Furthermore,

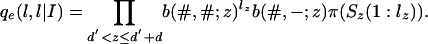Backward recursion. The backward recursion is obtained by defining

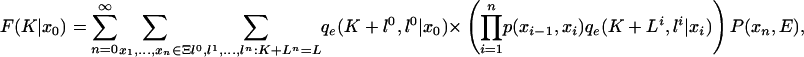[25]

which equals P(S(K + 1: L)|x₀). Separating out the sum over the first state x₁, we find

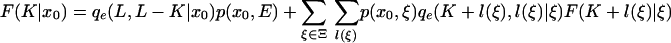[26]

for K <^w L and K ≤ L, and when K = L, the recursion is

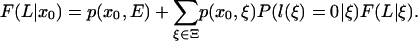[27]

A forward recursion can be derived in the same way. The details are described by Hein, Jensen, and Pedersen (6).

Reduction of complexity. For the recursions described in the previous subsection, we need to calculate F(K|x) for any value of K ≤ L. This takes of the order 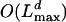steps. Each step here, however, involves the sum over l (see Eq. 26) and therefore requires of the order 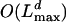steps. The time complexity of the algorithms is thus of the order 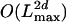. The algorithms are therefore inferior to those given in Approach 1. It turns out, though, that we can rewrite the algorithms in such a way that the resulting time complexity becomes 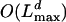and where the constant factor hidden by the O notation is slightly smaller than for the algorithms of Approach 1. We start by inserting Eq. 24 into recursion 26.

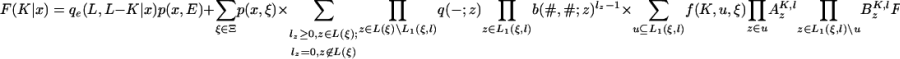[28]

where, as before, u is the subset of the leaves L₁ (ξ, l) at which we have survival from the ancestral inner node. If we let w be the subset of the leaves L(ξ)\u at which there is no survival, but the number of new links is positive, and we introduce the subset v of u ∪ w at which l_z ≥ 2, this gives

[29]

where 1(u ∪ w) is 1 when z ∈ (u ∪ w) and 0 when z ∉ (u ∪ w). The function G is defined as

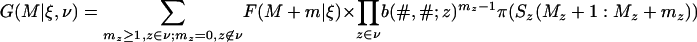[30]

for a nonempty subset v of L(ξ), and G(M|ξ, [null]) = F(M|\ξ).

We can obtain a recursion for G by splitting the sum in Eq. 30 into Σ_ṽ⊆v Σ_{mz≥2,z∈ṽ;mz=1,z∈(v\ṽ);mz=0,z∈/v}, where ṽ can be the empty subset. This gives

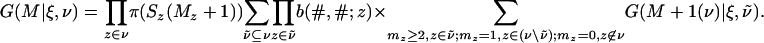[31]

Combining Eqs. 29 and 31, we have established a recursion involving the functions F(K|ξ) and G(K|ξ, v). For the tree in Fig. 1, the recursions of Algorithms involves 45 terms, whereas the number of terms for the recursions in this section is 24.

Discussion

This work presents algorithms that have the same complexity as the traditional nonstatistical multiple alignment algorithm in Sankoff (8). The statistical alignment approach to sequence analysis differs relative to the optimization approach in focusing on obtaining the probability of the sequences under the given model, rather than obtaining an alignment. Among molecular biologists, however, it is popular to consider the actual alignment, and the one chosen is typically the alignment that contributes the most to the probability of the observed sequences. The latter can be calculated by simple modifications of the central recursions of this work, where a summation operator is substituted by a maximization operator. Several additional problems have to be solved to make the algorithm of this paper useful in real data analysis. Besides actually implementing the algorithm, it needs to be coupled to a numerical optimization method to find maximum likelihood estimates of the unspecified parameters, such as branch lengths, substitution parameters, and insertion and deletion rates. This method can then be used to analyze up to, say, four sequence of realistic lengths (hundreds of base pairs/amino acids). Elementary computational tricks can extend this to six or seven sequences; beyond this, radically different methods will have to be applied. Jensen and Hein (9) suggested a simulation technique where the basic step is the simulation of the alignment of a three-star tree. The Gibbs sampler proposed by Holmes and Bruno (5) is based on samplings that require pairwise alignments only. This is a faster operation, whereas the Gibbs sampler proposed by Jensen and Hein (9) achieves a more efficient mixing per move. From the perspective of a biologist, the underlying model for this paper can be criticized. First, the assumption that all insertions/deletions are only one nucleotide/amino acid long does not conform to the biological reality and should be relaxed. Second, the assumption that all positions in a sequence evolve according to the same rates is also unrealistic. Formulating models and ways to calculate the relevant probabilities in such models is a major challenge to the field if a statistical approach to alignment is to be of widespread use.