Figure 4.

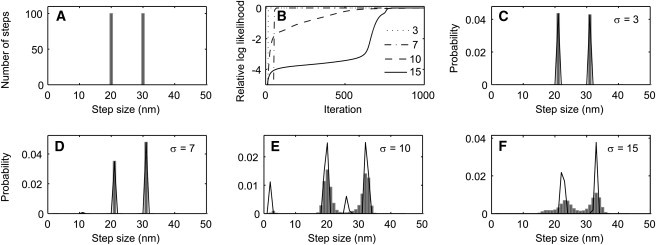
Estimation of a discrete step-size distribution in the presence of various levels of measurement noise; results from one representative simulation. A 2000-point time course was simulated consisting of 200 steps of either 20 or 30 nm and geometrically distributed dwell times with a mean of 10 sample points. (A) Step-size histogram of the 200 generated steps. (B) Convergence of L with a one-state HMM when the simulated time-course had 3, 7, 10, or 15 nm RMS of added Gaussian noise. The value of L after 1000 iterations was taken to be the maximum value. (C–F) Estimated step-size distributions from data having the indicated noise standard deviations σ. The final estimated step-size distributions c(w) (solid lines) and the distributions obtained after partial convergence, when L was 1 log-unit below its final value (solid bars), are plotted . The mean step sizes are recovered with high accuracy up to σ = 15 nm, although at a noise level of 10- or 15-nm spurious peaks in the distribution also appear. In this problem (n = 1, m = 160, T = 2000), each iteration required 1 s of CPU time using a 2 GHz processor.