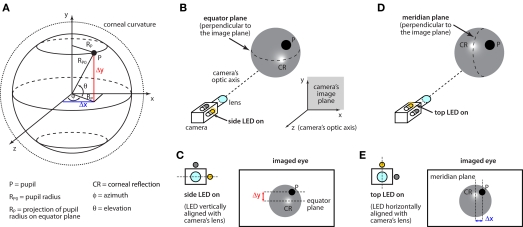
Figure 3.

Eye coordinate system and measurements. (A) The pupil (P) moves over the surface of a sphere (solid circle) of radius R_P0. Such a sphere is contained within a larger sphere – the extension of the corneal curvature (dotted line). The two spheres are assumed to have the same center (see text). The pupil position is measured in a polar coordinate system, whose origin is in the center of the corneal curvature. The orientation of the reference system is chosen such that the z axis is parallel to the optic axis of the camera and, therefore, the (x, y) plane constitutes the camera's image plane (see inset in B). The goal of the eye-tracking system is to estimate the pupil's elevation (θ) and azimuth (ɸ). This is achieved by measuring the distance Δy of the pupil from the equator plane (i.e., the plane that is perpendicular to the image plane and horizontally bisects the eye), and the distance Δx of the pupil's projection on the equator plane from the meridian plane (i.e., the plane that is perpendicular to the image plane and vertically bisects the eye). (B) In our imaging system, two infrared LEDs flank the imaging camera. When the side LED (which is vertically aligned with the camera's lens) is turned on, its reflection on the corneal surface (CR) marks the position of the equator plane. (C) Δy is measured as the distance between P and CR, when the side LED is turned on. (D) When the top LED (which is horizontally aligned with the camera's lens) is turned on, its reflection on the corneal surface (CR) marks the position of the meridian plane. (E) Δx is measured as the distance between P and CR, when the top LED is turned on.