Do Siblings’ Fertility Decisions Influence Each Other?

Abstract

Individuals’ fertility decisions are shaped not only by their own characteristics and life course paths but also by social interaction with others. However, in practice, it is difficult to disentangle the role of social interaction from other factors, such as individual and family background variables. We measure social interaction through the cross-sibling influences on fertility. Continuous-time hazard models are estimated separately for women’s first and second births. In addition to individual socioeconomic variables, demographic variables, and an unobserved factor specific to each sibling pair, siblings’ birth events and their timing enter as time-varying covariates. We use data from longitudinal population-wide Norwegian administrative registers. The data cover more than 110,000 sibling pairs and include the siblings’ fertility, education, income, and marital histories. Our results indicate that cross-sibling influences are relatively strong for the respondents’ first births but weak for the second parity transition.

Studies on fertility timing in developed countries give a strong explanatory role to individual life course transitions. These include such transitions as the end of educational enrollment, the start of or a change in career, geographical mobility, and transitions related to entry into and exit from marital and nonmarital coresidential partnerships. The postponement of and increasing variability in some of these processes has often been associated with the observed delay in childbearing. To account for fertility preferences in general, family background variables—or more generally, early life experiences—constitute key indicators (Axinn, Clarkberg, and Thornton 1994). However, individuals’ fertility behavior depends not only on family background variables and their life course paths but also on the behavior and characteristics of individuals with whom they interact in their families of origin as well as those with whom they are connected through social networks.

Several authors have emphasized the importance of social interactions for fertility choices (Bongaarts and Watkins 1996; Montgomery and Casterline 1996). Social interactions have at least three aspects: the exchange of information, the joint evaluation of its meaning, and social influence that constrains or encourages action (Bongaarts and Watkins 1996). A comprehensive survey on fertility and social interactions is documented by Kohler (2001). To understand the divergence in the demographic behavior of different populations with relatively similar environmental conditions, Kohler argued for a combination of economic fertility theory (based on individual optimal and rational decision rules) and theories on social interaction (which incorporate the behavior of other members of the community/society). The relevance of social interactions in the context of lowest-low fertility is emphasized in Kohler, Billari, and Ortega (2002). They found that all lowest-low fertility countries—that is, all countries with a total fertility rate (TFR) of less than 1.3—have experienced a sharp increase in the age at first birth. Further, they argued that this postponement cannot be explained by changing socioeconomic incentives alone: social interactions, either impersonal (e.g., through the labor market) or personal ones (e.g., through peer groups) must have induced multiplier effects or multiple equilibria. A further interesting demonstration of how social interaction can affect demographic behavior was given by Åberg (2003), who examined how the high school peers of young Swedes influenced their propensity to marry. She found positive effects of the proportion of peers married on the marriage rate, indicating that social interaction in part drives individuals’ marital decisions.

The measurement of social interaction and its influence on fertility decisions often fails because of the lack of appropriate data. In this article, we propose to use cross-siblings’ influences to measure social interaction effects in fertility behavior. Sibling effects on other social and demographic phenomena have been the focus of a large number of earlier studies. For example, Haurin and Mott (1990) investigated the cross-sibling effects on timing of sexual initiation, and East (1998) and East and Jacobson (2001) investigated the impact of teenage mothers on their youngest sibling’s pregnancy risk. Powers and Hsueh (1997) used a bivariate latent variable approach to study socioeconomic effects on the timing of a premarital birth. Later, Powers (2001, 2005) showed the effects of both socioeconomic indicators and family structure on the risk of a premarital birth. In fact, Rodgers and Rowe (1993) argued that regarding adolescent sexuality, siblings’ influence is greater than the influence by other peer groups.

In this article, we take a similar approach and test whether a sibling’s fertility behavior is related to the individual’s own fertility. Inspired by the theory of social comparison (Festinger 1954), which concludes that “[I]ndividuals tend to alter their behaviour or attitude to conform to those of others they perceive as similar in social structural positions or who share some characteristics that are relevant to the behaviour in question,” we argue that the cross-sibling influences on fertility rates can be substantial as a consequence of imitation, third-party pressures, and the exchange of information between siblings.

THEORETICAL CONSIDERATIONS ON SIBLING EFFECTS ON FERTILITY

In this section, we review theoretical arguments linking siblings’ fertility behaviors. We discuss three alternative, albeit not necessarily exclusive, mechanisms through which the fertility experiences of a sibling may affect a woman’s fertility.

A threefold argument about the existence of a correlation between siblings’ fertility desires and intentions is provided by Axinn et al. (1994); siblings have a common genetic component: siblings share socioeconomic characteristics and also environmental factors, such as schools, friends, and neighborhoods, through socialization. But, in addition to these factors that often go unmeasured, the authors argue that siblings may “provide salient behavioural examples to their brothers and sisters” (Axinn et al. 1994:68); that is, siblings serve as role models for their brothers and sisters. Such cross-sibling effects represent intrafamily social interaction mechanisms as opposed to external personal or impersonal social interactions. This argument on how intrafamily social interaction mechanisms may alter individuals’ fertility behavior is echoed in the literature on teenage childbearing: “. . . older siblings have the capacity to shape the sexual attitudes and norms of the younger children in the family, attitudes and norms that are thought to be key for younger siblings’ actual sexual behavior” (East 1998:66). The idea is partly based on the social learning theory proposed by Bandura (1977), in which he proposed three requirements for people to learn and model behavior. The requirements were observation of others’ behavior, the ability to reproduce that behavior, and motivation to adjust one’s own behavior in the direction of the others.

Although the example arguments put forward in the literature on teenage childbearing refer to siblings who live in the same household as adolescents, it is reasonable to extend this idea to situations in which the two siblings live in separate households but have some degree of contact with each other and each other’s families. Brothers and sisters are also likely to be relatively important peers for an individual in adulthood. Siblings might have a close relationship with the individual, nurtured over years of exposure, and these relationships may also become stronger throughout the life course as family relations are reinforced through transition rituals, such as weddings, baptisms and funerals. On the other hand, the cumulative contingencies of the life course might also weaken the bond between siblings. Regardless of how sibling relationships develop across the life course, their overall importance has been underlined by a wide range of psychological and sociological studies (Cicerelli 1995; Lamb and Sutton-Smith 1982). Finally, an important point is that social interaction effects arise not only from positive communication and exchange but also from siblings’ negative exchanges, such as jealousy, which play an important role (East 1998).

Siblings’ experiences will be well known to the individual and are therefore an important source of information on life course transitions, such as union formation and fertility (Bernardi 2003). Thus, when a woman observes her sibling pass through the transition from childless to parenthood through a higher-parity transition (and possibly also an adoption process), this life event might influence the individual’s desire to have own children. Our first hypothesis is that social interaction, as represented by the cross-sibling effects, has a measurable effect on first-birth rates.

Cross-sibling effects may be at their strongest for the first birth. Our reasoning behind this is as follows. The transition into motherhood constitutes a unique experience in one’s life course. Social influence might play an important role to resolve the uncertainty associated with the consequences of motherhood. By learning how siblings cope with their new role as mothers, and by experiencing the company of young children and possibly being involved in the childcare of the sister’s baby (East 1998), the desire for motherhood might be triggered. At higher-order parities, the woman and her partner have obtained experience with having and caring for a baby. At this stage of the life course, social interaction with siblings and others may be less important for the exchange of information about fertility and pregnancies. After all, the woman has already had such an experience herself. Thus, progression to a second or higher-order child may constitute a transition that is rather influenced by own socioeconomic characteristics and, to a lesser extent, by factors external to the woman and her household. Another reason to expect a smaller impact of the sibling’s fertility decisions for higher-order births is what could be called “life course bifurcation.” With progressing time, the siblings might take similar but not identical life course decisions: their situations might diverge to an extent such that their influence on each other is reduced or disappears. As both siblings progress through their life course experiencing various demographic and economic events that have implications for fertility-related decision making, such as union formation and disruption or employment and education events, the variance across siblings in the timing of same-order births is likely to increase. For their first birth, the variance in siblings timing will be low, when all other relevant factors (such as their ages and age difference) are controlled for. This argument of path-dependency in life courses is similar to what life course researchers working on negative socioeconomic and demographic outcomes have denoted as “cumulative contingencies” (Mayer 1986). Thus, our second hypothesis is that cross-sibling effects are stronger for the first birth than they are for subsequent births.

Moreover, it is easily conceivable that these relations depend on the time passed since the sibling’s birth of a child. For example, it is likely that a birth to a sibling might have a positive effect on an individual’s hazard of birth in the short run yet have no effect or a negative effect in the long run. The third hypothesis that we put forward is thus that the effect of a sibling’s birth is immediate, but the effect becomes less important in the long run.

In addition to intrafamily mechanisms of social interaction, cross-sibling effects on fertility may be associated with parental pressure and life-course sequencing norms. A large literature exists on the potential effect that parents might have on their adult children’s childbearing and family decisions: for example, studies examining mothers of child bearing teenagers suggest that mothers treat their childbearing teenagers differently from their childless siblings (East and Jacobson 2001,East and Jacobson 2003). Additionally, studies of mothers’ preferences for family behaviors suggest that mothers affect daughters by guiding them toward different paths to adulthood (Barber 2000). For example, parents may exert pressure on their children favoring entry into parenthood to provide grandchildren (Bernardi 2003). After one of two siblings has a child, their parents have the desire for at least one grandchild fulfilled. This could lower the pressure on the sister that still is childless, but it is also conceivable that the pressure might be even stronger after the birth of a niece or nephew because the woman now is “lagging behind” her sister. Originating from the woman’s failure to meet expectations of role transitions, such an effect would most likely be found for the transition to parenthood (i.e., first birth), and less likely be found for second births.

METHODS AND DATA

Our strategy is to model a woman’s births by using continuous-time piecewise linear hazard models, where the dependent variable is a hazard, or an instantaneous rate, that might vary over time. Her sibling’s fertility outcomes enter the right side of the equation as time-dependent variables together with other relevant controls. We also include a stable common unobserved factor, which is unique to each sibling pair (e.g., factors that the siblings share, such as characteristics of their family, genes, and so on).

Available Data

The data come from Norwegian administrative registers, which cover all who at some point resided in Norway since 1963. A system of personal ID numbers uniquely identifies each individual and provides links between an individual and his/her parents. This facilitates proper identification of siblings and their parents in the population register.

In this article, we will consider only sibships of two (i.e., persons with only one sister or brother). The reason for this restriction is that including sibships three or higher would make data construction and modeling unnecessarily complex. This implies, of course, that we can neither generalize to all individuals nor to individuals with multiple siblings. A further restriction is that both siblings must have been born between 1955 and 1975. Their age difference is thus also restricted to a maximum of 19 years. After sibships and siblings are identified, we link (again using the personal ID number system) further information from various registers to the data set. This information includes, but is not limited to, the siblings’ fertility histories, time series of their income, educational attainment, educational enrollment, and marital status. The information on marital status, unfortunately, does not distinguish between singles and individuals who are cohabiting. Cohabitation is very popular in Norway, and a majority of children are born out of wedlock. However, there are few reasons to believe that this problem represents a serious threat to the validity of our results.

Selected descriptive statistics of the data are given in Table 1. Our final data set contains records of 111,582 sibships, with information on both siblings in each record. Most siblings are quite close in age, with about one-half having an age difference of 2–3 years. In total, 144,120 first-birth spells are included in the estimation of our first-birth model. The corresponding number for second births is 108,647. During their exposure to first and second births, 70% or more of women had a sibling who had a first birth. Note that apart from the woman’s logged income, the distributions of control variables are calculated on the basis of all person-months of exposure. As we follow each individual woman from age 15 onward, there is quite a long period for almost every woman spent in the single state with low education and low income.

Table 1.

Data Overview and Selected Descriptive Statistics

Variable	First Birth	Second Birth
Number of Sibships in Estimation	111,582
Age Gap Between Siblings (in % of all sibships)
10 or more years	1.6
9 years	1.0
8 years	1.7
7 years	3.0
6 years	5.4
5 years	9.9
4 years	17.5
3 years	24.5
2 years	23.8
1 year	10.5
0 years	1.1
Number of Spells Used in Estimation	144,120	108,647
Sibling’s Birth Outcomes (%)
First birth	70	73
Second birth	51	55
Third birth	17	18
Distributions of Other Included Covariates
Mean of logged income (SD)	2.87 (1.64)	3.59 (1.35)
Cohort (%)
55–59	14.3	22.3
60–64	23.6	27.8
65–69	33.2	31.2
70–74	28.8	18.2
Educational attainment (%)
Primary	15.3	8.7
Secondary	60.3	61.3
Some college	21.7	26.3
College graduate	2.7	3.7
Educational enrollment (%)
No	72.6	91.6
Yes	27.4	8.4
Marital status (%)
Single	93.3	51.5
Married	5.5	40.0
Previously married	1.2	8.7

Estimation, Model, and Variable Specifications

Continuous-time hazard models are estimated for the first- and second-birth rates. Each birth rate is assumed to be piecewise linear in the log hazard. That means that in defined intervals, the log hazard is increasing or decreasing linearly with an unknown coefficient. The baseline coefficients, which are (1) age at first birth for the first-parity transition, and (2) time since last birth for higher-parity transitions, are estimated along with other parameters of the model. Note that the duration in both cases is the duration from entry into the risk set (age 15 for the first birth; the time of first birth plus three months for the second birth) up to a conception leading to a live birth. Thus, the duration of pregnancy does not contribute to the duration variable. The women included in the estimation are all followed from age 15 and censored when they reach age 45. The models on first and second birth risks are almost identical, with the only differences being in the baseline pattern (different nodes for the spline) and the inclusion of a spline capturing effects of the woman’s age in the model for the second birth. Both models are estimated by using aML v2.09 (Lillard and Panis 2002). Mathematically, the models for the two rates follow these forms:

$$\text{log}\hspace{0.17em}h(t_{ij})={\gamma }_1^{\text{'}}D(t_{ij})+{\gamma }_2^{\text{'}}P(t_{ij})+{\mathbf{\beta }}_1^{\text{'}}{\mathbf{\text{X}}}_{ij}+{\mathbf{\beta }}_2^{\text{'}}{\mathbf{\text{Z}}}_{ij}(\mathbf{\text{t}})+\sum _{s=1}^3{\lambda }^{\text{'}}{E}_s(t_{ij})+{\varepsilon }_j$$ (1)

$$\text{log}\hspace{0.17em}h(t_{ij})={\gamma }_1^{\text{'}}D(t_{ij})+{\gamma }_2^{\text{'}}A(t_{ij})+{\gamma }_3^{\text{'}}P(t_{ij})+{\mathbf{\beta }}_1^{\text{'}}{\mathbf{\text{X}}}_{ij}+{\mathbf{\beta }}_2^{\text{'}}{\mathbf{\text{Z}}}_{ij}(\mathbf{\text{t}})+\sum _{s=1}^3{\lambda }^{\text{'}}{E}_s(t_{ij})+{\eta }_j.$$ (2)

Subscripts i and j denote the sibling and the sibship. All the parameters vary across Eqs. (1) and (2). The terms D(t_ij), A(t_ij) and P(t_ij) are piecewise linear splines for the main duration baseline, the woman’s age, and period. The terms γ′₁–γ′₃ represent the vectors of corresponding coefficients. X and Z(t) represent observed time-constant and time-varying covariates, and β′₁ and β′₂ represent the corresponding regression coefficients. The term E_s(t) represents a piecewise linear spline for sibling’s birth s, and λ′ is an associated vector of coefficients. The total sibling influence is parameterized as a set of as many as three such splines, one for each of the sibling’s childbirths, that begins when the sibling’s first childbirth takes place. The spline has two nodes, at 12 and 36 months, and thus three slopes. This means that the effect, if any, is allowed to vary with time, allowing us to uncover any time dependencies in the influence of sibling’s fertility outcomes on a woman’s rate of first and second birth. For every birth that a sibling experiences, one spline enters the model additively. Consider this example: woman (A) has a sister (B) who gives birth to two children within a three-year period. In the time leading to the sister B’s first birth, woman A’s fertility is not affected by any sibling effect. After B’s first birth, A’s fertility rate will be affected by the effect of one spline, with a magnitude of the effect depending on how much time passed since that birth took place. When B’s second baby is born, however, A’s fertility rate will be affected by the cross-sibling influence coming from the births of both the first and the second child. The effects will be different because the time that has passed since the sibling’s birth events is different.

In each model, we also include a family-specific unobserved factor that is shared by the individual and her sibling. By including this random effect, we control for time-constant unobserved factors that the siblings share because of their similar socialization, childhood experience, and other characteristics either socially and biologically (genetically) transmitted from their parents. Each of the two random variables (denoted ɛ_j and η_j in Eqs. (1) and (2)) is assumed to have a normal distribution, with a mean of zero and a variance to be estimated. To properly estimate the variance of the distribution, we must have at least two observations for some sibships. In addition, we include a number of other independent variables because some of these might confound the relationship between the sibling birth and own fertility, and others might temper the effects of the sibling influence. Included are educational attainment, current educational enrollment, logged income, and dummy variables for being married or previously married. All these variables are time varying and are annually updated after 1980, although income and marital status are time varying from 1970. Finally, we also include dummy variables for five-year cohort groups, the siblings’ birth order, the sibship sex mix, and the age difference in years between the focal individual and her sibling.

An important aspect is that we estimate the models for women only. The reason for this is the very different age profiles and relevant control variables for men’s fertility compared with women’s fertility. This means that for mixed-sex sibships (brother and sister), we use only one of the siblings (the woman) included in the estimation. The other (male) sibling will not contribute to the estimation apart from the effects of his fertility outcomes on his sister’s likelihood of conception. Thus, the unobserved factor is identified solely on the basis of observations of women. All-male sibships are then, of course, excluded from the analysis. This implies that i can vary from 1 to 2 in female-female sibships and is by definition 1 in female-male sibships, while j takes values from 1 to the number of all sibships included in the model.

Finally, there are some concerns related to historical period. The general conditions for having children may vary over time with business cycles, expansion of the Norwegian parental leave system, and so on. These factors affect all individuals’ fertility rates at the same time. Therefore, we control for shifts in fertility rates between periods. We include a piecewise linear spline that allows for almost any type of period variation in fertility.

A Note on Identification of Cross-Sibling Effects

Social interaction effects constitute an important field of research in social sciences. However, in practice, it is often difficult for social scientists to disentangle the role of social interaction from other factors, such as individual and family background variables as well as macro-level indicators that may also shape fertility decisions.

The focus of this article is on the relationship between one person’s fertility and the fertility of that person’s sibling. The most intuitive way of modeling such influences is to model the outcome of one individual as a function of the earlier behavior of one or more other individuals, as we do here. Independent of whether any such relationship arises through imitation, social pressure, information exchange, or some other form of social interaction, the association between own and sibling’s fertility will fall into the category of endogenous effects as discussed by Manski (1995). Endogeneity, in this respect, refers to the fact that sibling’s fertility influences a woman’s fertility but also appears as a dependent variable on the left side of our regressions. The identification of such endogenous effects has been shown to be very problematic for continuous and discrete outcomes (Kravdal 2003). Manski (1995) argued that there might be more promise in identifying endogenous effects with dynamic models, such as the hazard rate models that we apply here.

RESULTS AND DISCUSSION

Table 2 shows our main results for the hazard of a first and second birth, net of control variables, and the complete set of parameter estimates are listed in Table 3. As seen in Table 2, we find significant effects of the sibling’s fertility on women’s first-birth rate. All estimates of parameters for the effect of a sibling’s birth on the woman’s fertility rate are statistically significant. The first parameter for the initial 12-month period after the birth is positive, and the parameters for the subsequent periods are negative. For second births, however, the parameter estimate for the second and third years following the sibling’s birth is insignificant, and that for the third year onward is barely significant. The magnitude of the estimates is also much smaller than for the first birth.

Table 2.

Parameter Estimates for the Influence of a Sibling’s Birth Events on the Log-Hazard of Conception Leading to a Live Birth, Net of Control Variables

Parity Transition	Time Since Sibling’s Birth
	Up to 12 Months	12 to 36 Months	36 Months Onward
First Birth	0.0702***	–0.0246***	–0.0007***
Second Birth	0.0043***	–0.0003	–0.0001*

Note: All parameters are spline slopes indicating change in log-hazard per month.

^*p < .05;

^**p < .01;

^***p < .001

Table 3.

Complete Results From Hazard Models of First- and Second-Birth Rates

Variable	Category/Slope	First-Birth Model		Second-Birth Model
		Parameter	SE	Parameter	SE
Intercept		–5.68	0.92	–3.35***	0.38
Duration Spline (age or time since first birth)		0.02***	0.00	0.07***	0.00
		0.01***	0.00	–0.02***	0.00
		0.00***	0.00	–0.01***	0.00
		–0.01***	0.00
		–0.02***	0.00
Age Spline	Up to 35			0.00***	0.00
	35 and older			–0.03***	0.00
Period Spline
	1970–1975	–0.01***	0.00	–0.02***	0.01
	1975–1980	–0.02***	0.00	0.00	0.00
	1980–1985	0.00***	0.00	0.01***	0.00
	1985–1990	–0.01***	0.00	–0.01***	0.00
	1990–1995	0.01***	0.00	0.01***	0.00
	1995–2003	0.00***	0.00	0.00***	0.00
Mother’s Birth Cohort	Up to 1919	–0.08***	0.02	0.05**	0.02
	1920–1934	0.00		0.00
	1935–1949	0.22***	0.01	–0.05***	0.01
	1949 and later	0.60***	0.02	–0.01	0.03
Marital Status	Not married	–1.06***	0.01	–0.49***	0.01
	Married	0.00		0.00
	Previously married	–0.69***	0.03	–0.54***	0.02
Educational Attainment	Primary	0.04***	0.01	–0.18***	0.01
	Secondary	0.00		0.00
	Some college	0.02***	0.01	0.33***	0.01
	College graduate	0.11***	0.02	0.47***	0.02
Educational Enrollment	No	0.00		0.00
	Yes	–0.49***	0.01	–0.42***	0.02
Log Income		0.28***	0.00	0.07***	0.00
Birth Cohort	1955–1959	0.00		0.00
	1960–1964	0.11***	0.01	0.10***	0.02
	1965–1969	0.13***	0.02	0.15***	0.03
	1970–1974	0.05	0.03	0.10***	0.04
Sibship Position	Has younger sister	0.00		0.00
	Has older brother	0.07	0.06	0.05	0.07
	Has younger brother	0.05***	0.01	0.01	0.01
	Has older sister	–0.02	0.06	0.02	0.07
Sibling’s Birth Event Spline	0–12	0.0702***	0.0058	0.0043***	0.0012
	12–36	–0.0246***	0.0029	0.0003	0.0006
	36+	–0.0007***	0.00003	0.0001*	0.00005
Age Difference of Siblings	–10 or more years	0.36***	0.05	0.03	0.06
	–9 years	0.22***	0.06	–0.04	0.07
	–8 years	0.22***	0.06	–0.02	0.07
	–7 years	0.17***	0.05	0.06	0.06
	–6 years	0.19***	0.05	–0.01	0.06
	–5 years	0.19***	0.05	–0.01	0.06
	–4 years	0.18***	0.05	0.05	0.05
	–3 years	0.18***	0.05	0.08	0.05
	–2 years	0.16***	0.05	0.09*	0.05
	–1 years	0.18***	0.05	0.08	0.06
	0 years	0.00		0.00
	1 years	0.16***	0.04	0.07	0.05
	2 years	0.10**	0.04	0.05	0.05
	3 years	0.07*	0.04	0.03	0.05
	4 years	0.07	0.04	0.00	0.05
	5 years	0.06	0.04	–0.01	0.05
	6 years	0.05	0.05	–0.02	0.05
	7 years	0.01	0.05	–0.06	0.06
	8 years	0.04	0.05	–0.06	0.06
	9 years	–0.04	0.06	–0.02	0.07
	10 or more years	–0.07	0.06	–0.14**	0.07
Family-Specific Heterogeneity		0.27***	0.02	0.30***	0.02
Log-Likelihood		–618,651		–401,574

Notes: All parameters for variables referred to as splines are slopes indicating change in log-hazard per month. The duration spline has knots at different places in the two models. Each estimated parameter represents a slope between two knots. For first births, the knots are at 20, 25, 30, and 35 years of age. For second births, the knots are at two and five years passed since coming under risk for the first birth.

^*p < .05;

^**p < .01;

^***p < .001

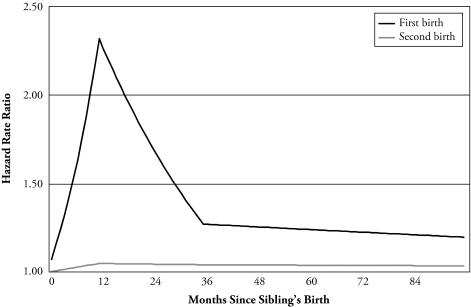
The results are displayed graphically in Figure 1, where we plot the obtained estimates of the cross-sibling influence on fertility for the first- and second-birth (or conception) risks over the first eight years after a sibling’s birth. The slope for the first year after the sibling’s birth is positive and leads to a cumulative increase in the log-hazard of first conception by 0.07 per month. One year after the birth of the sibling’s child, the risk starts to decline. During the next two years, the component of the log-hazard of conceiving her first birth that is attributable to the sibling’s fertility decreases by 0.025 for every month passed. After three years, the risk is much closer to the risk for women who still have a childless sibling. It continues to decline over the following years. These results suggest that important cross-sibling influences exist on the transition to motherhood, as our first hypothesis states.

Figure 1.

Influences of a Sibling Birth on a Woman’s Hazard of First and Second Conception Leading to a Live Birth, Net of Control Variables

A comparison between the results for first- and second-birth rates supports our second hypothesis that argues for cross-sibling effects to be at their strongest for the transition to motherhood—that is, the first-birth rate—compared with the transition to parity 2. The differences between the effects are striking. If we consider the effects of sibling’s fertility when they are at their strongest, the relative risk of a first birth is more than double and the relative risk of a second birth is only 5% higher than for those with childless siblings (cf. Figure 1). Another possible reason to expect a smaller effect on second-birth rates is norms on birth spacing. If norms exist for close spacing of the first and second births, there will be little room for a sibling effect on second births.

Our results also lend support to our third hypothesis. The sibling effects for the first birth decline steeply 12 months after the conception. We thus conclude that the cross-sibling impact on fertility is immediate: that is, a sister or brother having children affects a woman’s fertility in the short run and is less important in the long run. The effect of a sibling’s birth on the first-birth rate seems to become negative in the very long run.

The results are obtained with data on pairs of siblings, which implies that generalizations to individuals with no siblings may be problematic. It is likely, however, that effects similar to those we describe in this study operate in other, nonfamily close relationships. Although individuals without siblings cannot be affected by the intrasibship mechanisms, they may be affected by the behavior of others.

Most of the other variables included in the model behave as expected (see Table 3). The duration patterns conform to what we have seen in other studies of first- and second-birth rates from Norway and comparable countries. Educational enrollment has a negative effect on birth rates, and educational attainment shows up as a positive predictor. This effect is strongest for second births and has been found to be a result of selectivity by Kravdal (2001). Coefficients for the various marital states also fall into the expected pattern of married women having a higher fertility than divorced and single women. Period effects show a decrease in first-birth rates until 1980. Any pattern beyond this is hard to identify from the results. For the age variable, we find that the hazard of a second birth for women at risk declines quickly after 35 years of age. Having a relatively young mother seems to increase the risk of a first birth substantially. This suggests the existence of an intergenerational transmission of fertility behavior. Women who are currently enrolled in school have a substantially lower rate of first births than those who are not.

It is important to be aware of how our selection of sibships of two who were born within certain cohorts will affect our results. Being a child of a mother of two children when larger families were the norm could very well affect the woman’s childbearing decisions. For example, the mothers of the siblings in our data set are likely to include disproportionate numbers of working women and women with higher educational attainment because they restricted their fertility to only two children. Finally, this restriction might limit the external validity of our findings. Individuals with either a lower number of siblings or a higher number of siblings might react differently to a sibling’s birth than individuals who have only one brother or sister.

CONCLUSIONS

This article provides an analysis of how a woman’s fertility decisions are influenced by her sibling’s fertility outcomes. Continuous-time hazard models were estimated for the first- and second-birth rate. Our results suggest that cross-sibling effects exist on the Norwegian first-birth rate. The corresponding results for the second-birth rate are close to negligible. This indicates that the social interactions, however they operate, play their most important role at the onset of motherhood but are less important for later births. Our findings also lend support to the idea that uncertainty around the process of entering parenthood can be reduced by observing a sibling’s experience with the same transition. The fertility experiences of a woman’s sibling seem mostly to have an immediate and less-permanent effect on the woman’s fertility.

Future research needs to identify the mechanisms through which peer groups effects—such as the link between siblings’ fertility decisions—operate. Serious limitations to this type of inquiry remain, and the actual mechanism behind any sibling effect will, in most cases, remain invisible to researchers. This study, for example, does not establish whether sibling effects arise because of social imitation or information exchange. Qualitative evidence might point to what mechanisms are most important. Moreover, because siblings are a special group of peers, our results should not be generalized to apply to peer group effects overall. However, the fact that we could discern a rather pronounced influence on siblings’ fertility indicates that peer group effects should not be neglected in fertility research. As a next step, new data that also include information on the fertility of close relatives, friends, and other colleagues need to be gathered, particularly in developed countries where these kinds of data are still largely missing. Finally, the finding that individuals’ birth rates depend positively on siblings’ fertility might lead to a rather pessimistic implication in low-fertility countries that are characterized by increasing shares of families with one child only. In such a situation, the positive influence of a sibling’s fertility behavior is not present, possibly driving down fertility even further. The fertility trap hypothesis put forward by Lutz, Skirbekk, and Testa (2006) argued that such a development might take place, and our work sheds light on one of the mechanisms behind it.