Abstract
The stabilization of RNA tertiary structures by ions is well known, but the neutral osmolyte trimethylamine oxide (TMAO) can also effectively stabilize RNA tertiary structure. To begin to understand the physical basis for the effects of TMAO on RNA, we have quantitated the TMAO-induced stabilization of five RNAs with known structures. So-called m-values, the increment in unfolding free energy per molal of osmolyte at constant KCl activity, are ~0 for a hairpin secondary structure and between 0.70 and 1.85 kcal/mol/m for four RNA tertiary structures (30 – 86 nts). Further analysis of two RNAs by small angle X-ray scattering and hydroxyl radical probing shows that TMAO reduces the radius of gyration of the unfolded ensemble to the same endpoint as seen in titration with Mg2+, and that the structures stabilized by TMAO and Mg2+ are indistinguishable. Remarkably, TMAO induces the native conformation of a Mg2+ ion chelation site formed in part by a buried phosphate, even though Mg2+ is absent. TMAO interacts weakly, if at all, with KCl, ruling out the possibility that TMAO stabilizes RNA indirectly by increasing salt activity. TMAO is, however, strongly excluded from the vicinity of dimethylphosphate (unfavorable interaction free energy +211 cal/mol/m for the potassium salt), an ion that mimics the RNA backbone phosphate. We suggest that formation of RNA tertiary structure is accompanied by substantial phosphate dehydration (loss of 66 – 173 water molecules in the RNA structures studied), and that TMAO works principally by reducing the energetic penalty associated with this dehydration. The strong parallels we find between the effects of TMAO and Mg2+ suggest that RNA sequence is more important than specific ion interactions in specifying the native structure.
Keywords: hydration, dimethylphosphate, RNA folding, linkage relations
INTRODUCTION
Osmolytes are small organic molecules that, together with ions, are accumulated or synthesized by cells to maintain an appropriate turgor pressure.1; 2 The propensity of many osmolytes to affect protein stability has been extensively studied.3; 4; 5 So-called protecting or compatible osmolytes tend to be excluded from solvation layers around the protein backbone, which creates an energetic penalty for exposing peptides to solvent when high concentrations of osmolyte are present. These osmolytes therefore favor protein folding into more compact structures with buried (solvent-inaccessible) backbone.6; 7; 8; 9 The protecting osmolyte trimethylamine oxide (TMAO) is particularly effective in forcing thermodynamically unstable proteins to fold into native, functional structures.10; 11 In a survey of osmolyte effects on RNA stability, we found that TMAO effectively stabilized all the RNA tertiary structures examined, but had a small destabilizing effect on secondary structure.12 We hypothesized that TMAO stabilizes RNA by an analogous mechanism as deduced for proteins, viz., unfavorable interactions between TMAO and the sugar-phosphate backbone stabilize more compact conformations of an RNA.
In this work, we quantitate the stabilization of four different RNA tertiary structures by TMAO in KCl solutions, and in closer examination of two of these RNAs find strong parallels between the effects of Mg2+ and TMAO: both promote more compact conformations of partially unfolded RNAs, and ultimately stabilize the identical tertiary structure. While Mg2+ favors compact RNA conformations by reducing electrostatic repulsion between phosphates, we suggest that TMAO reduces the energetic penalty associated with phosphate dehydration. This suggestion is supported by our measurement of a strong exclusion of TMAO from the vicinity of an RNA backbone mimic, dimethylphosphate, and estimates of the number of hydrating water molecules that are released upon folding of RNA tertiary structures. Our conclusions emphasize the role of phosphate desolvation in the formation of RNA tertiary structure, and the dominant role of sequence (rather than specific ion interactions) in specifying the native structure.
Background
Linkage relations for salt and osmolyte effects on RNA stability
RNA stability is very sensitive to salt concentration. Osmolytes therefore have the potential to shift RNA folding equilibria in two ways: directly, by favorable or unfavorable interactions with the RNA itself, and indirectly, via osmolyte – ion interactions that change the effective concentration of the ions. In this section, we summarize the thermodynamic framework we use to distinguish the effects of salt and osmolyte on RNA folding. Note that we use molal concentrations throughout this work, rather than the more familiar molar units. One reason for doing so is that water concentration is a constant in molal units. Titration of osmolyte into a salt solution of constant molality therefore does not change the mole ratio of salt to water.
We define an observed equilibrium constant for RNA unfolding as Kobs= mU/mF, where mF and mU are molal concentrations of folded and “unfolded” RNA conformations, respectively. The equilibrium may be between a duplex and single-stranded RNA or between the native tertiary structure and a partially unfolded RNA with substantial secondary structure. (Partially unfolded states of an RNA have sometimes been called intermediate or I states, to distinguish them from a single stranded, fully unfolded conformation.13 For convenience, we use U to refer to either partially or fully unfolded RNAs, depending on the folding reaction under consideration.) The solutes of interest here, salt and osmolyte, affect Kobs because of their differential interactions with folded and unfolded states of the RNA. All ions interact with RNA by long-range electrostatic forces, attractive for cations and repulsive for anions, although other factors (such as hydration changes) may also come into play for cations. Osmolytes compete with water for solvation of the RNA; they may be either accumulated or excluded from the RNA surface depending on whether the affinity of different RNA groups (bases, sugars, phosphates) is greater for osmolyte or water, respectively. For either ions or osmolytes, it is convenient to characterize the RNA – solute interaction in terms of an interaction coefficient,
| (1) |
where mS is the molality of a solute, mRNA is the RNA molality, and μS is the solute chemical potential. (In eq 1 and all following partial derivatives, temperature and pressure are also held constant.) The solute s may be the cation, anion, or osmolyte (here abbreviated +, −, or TMAO). Each Γs corresponds to the change in molal concentration of solute necessary to maintain its chemical potential (μs) at a constant value when the concentration of the RNA changes.
Linkage relations 14; 15 equate changes in the interaction coefficient with the sensitivity of the folding reaction to solute activity (as). For solutions containing TMAO and KCl, the relations are
| (2a) |
| (2b) |
where a± is the mean ionic activity of KCl and the superscripts F and U signify folded and unfolded forms of an RNA, as defined above. (Kobs for a nucleic acid conformational change tends to follow a power law with respect to its dependence on salt activity, which is conveniently expressed as the log-log relation in eq 2b; osmolyte effects on ln(Kobs) tend to be approximately linear in osmolyte activity.) The ΔΓ terms may be thought of as the uptake or release of TMAO or KCl that accompanies the RNA folding reaction. Note that both cations and anions participate in the folding reaction; the term 2ΔΓ± is used to emphasize that there must be identical uptake or release of cations and anions to maintain charge neutrality.16
RNA stability may be measured as a function of TMAO concentration at a constant KCl concentration, or vice versa, but eqs 2a and 2b are in terms of TMAO and KCl activities. To use the linkage relations, we have to first relate changes in concentration (e.g., ∂lnmKCl) to changes in activity (∂lnaKCl), and then take into account any mutual interaction between TMAO and KCl that would cause the activity of KCl to change when its concentration is held constant and TMAO is titrated (eq 2a; there is a reciprocal problem in maintaining constant aTMAO in eq 2b). There are limiting cases in which we are able to apply the linkage relations to experimental data. One is the salt dependence in the absence of TMAO:
| (3) |
SKobs is the experimentally determined dependence of ln(Kobs) on ln(mKCl); it is constant within experimental error with the RNAs and salt concentration ranges used here (0.025 – 0.8 m). ε± is related to the dependence of the KCl activity coefficient on KCl concentration; from literature data, a value of −0.106 is appropriate for KCl concentrations up to ~0.5 m, and −0.107 for concentrations between 0.1 and 0.8 m.16
Two useful quantities are derived from a limiting value of ΔΓTMAO. We first assume (following the work of Hong and Record17; 18) that the activity coefficient of TMAO is constant with respect to TMAO molality in the limit of low TMAO concentration (but still large excess over RNA). The activity coefficient then factors out of eq 2a when mTMAO → 0,
| (4) |
It is still necessary to relate the derivative at constant salt activity to one at constant concentration. An additive correction factor (derived in 17; 18) accounts for any effect of TMAO on the KCl activity:
| (5a) |
| (5b) |
μKCl-TMAO is the chemical potential derivative that quantifies interactions between KCl and TMAO; its measurement by osmometry is described below. (The limit mTMAO → 0 applies to the value used for μKCl-TMAO.) Equation 5a was multiplied by −RT (R is the gas constant, T the temperature) and combined with eq 4 to put the expression in terms of the observed folding free energy, ΔG°obs (eq 5b). This form of the equation is the same as the “m-value” frequently used to report the effects of osmolytes on protein stability, with the exception that molal concentrations are used here, instead of the more common molarities.5; 8; 19
Protecting osmolytes such as TMAO tend to be excluded from the surface of a protein or RNA (Γs is negative). If an osmolyte is so strongly excluded that the concentration of osmolyte within a solvation layer around the macromolecule is negligible compared to osmolyte concentration in bulk solvent, then it is simple to relate the number of excluded osmolyte molecules, Γs, to the number of water molecules from which the osmolyte is excluded, B1:
| (6) |
This formula has been derived in several different ways; see 15 for references and comments. Combining eqs 5a and 6, the release or uptake of waters of solvation associated with a folding reaction is
| (7) |
where 55.5 is the molality of water. As with eq 4, eq 7 applies in the limit mTMAO → 0. ΔB1 will be larger than calculated by eq 7 if TMAO is not completely excluded from solvation layers around the RNA.
Measurement of TMAO-solute interactions by vapor pressure osmometry
Vapor pressure osmometry (VPO) measures the partial pressure of water in equilibrium with a solution. The result of the measurement is reported as the solution osmolality,
| (8) |
where m•water ≡ 55.5 mol/kg, the molality of water, and awater is the thermodynamic activity of water in the solution being measured, as derived from the ratio of the partial pressure of the solution to that of pure water. Osmolality is identical to molality if the solute(s) present in solution behave ideally, i.e. the activity coefficient of each solute γi = 1. According to the Gibbs-Duhem equation for a two-component solution, any deviation from ideal behavior of one component is accompanied by a reciprocal deviation by the other component. Thus, the dependence of the solution osmolality on solute concentration can be used to calculate the solute activity coefficient.20
In solutions with several solutes, the deviation of the measured osmolality from ideality contains information about interactions between all the different solutes. In principle, the strengths of all the interactions can be quantified from water vapor pressure measurements alone, as long as a large enough matrix of solute concentrations is measured to high enough accuracy.21 As a practical matter, only pairwise interactions in a three-component system (water plus two solutes) can reliably be extracted. The data analysis needed to obtain the relevant parameters has been discussed extensively.22; 23; 24 Briefly, the osmolality (Osm) of solutions with varying concentrations of two solutes is compared with the osmolalities of solutions containing only one solute to obtain the difference ΔOsm,
| (9) |
where the subscripts 2 and 3 refer to the two solutes (water is component 1). The chemical potential derivative μ23 is defined and related to ΔOsm measurements by24; 25
| (10) |
μ23 can be decomposed into two terms,
| (11) |
is derived from the ideal mixing entropy and is independent of the chemical nature of the solutes; the excess potential originates in the interactions between solutes that cause the solution to deviate from thermodynamic ideality.23; 25 For the concentration ranges of solutes used in the VPO experiments reported here, the contribution of the mixing entropy is small, for neutral solutes and −0.0342 for the salt K-DMP (see eq 5 of reference 25).
RESULTS
RNAs selected for this study
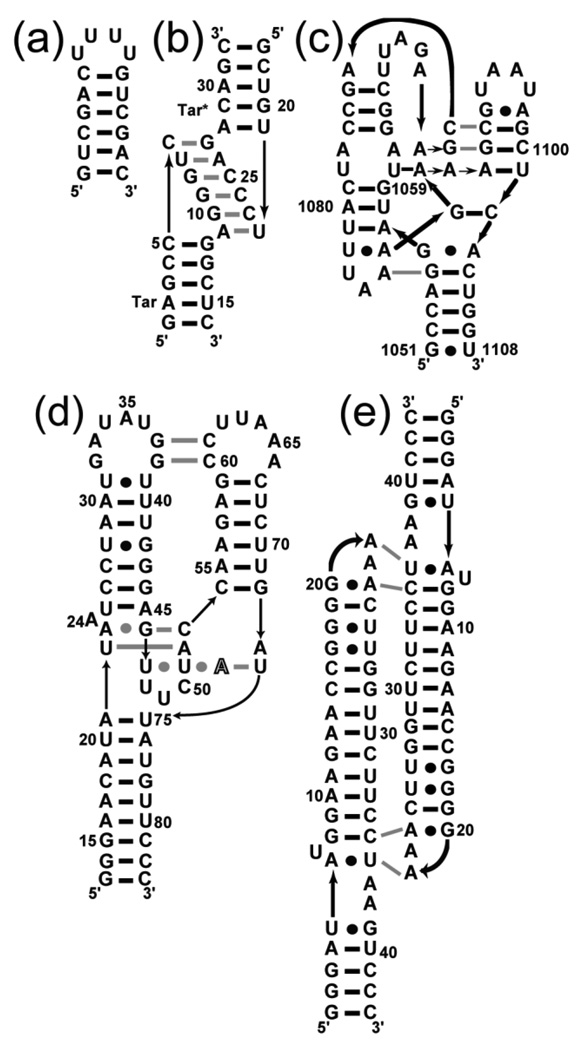
Five RNAs (Figure 1) were chosen to investigate the effects of TMAO on structure stability. A short hairpin was designed to be a representative secondary structure with both A-U and G-C base pairs (Figure 1A). The other four RNAs all contain naturally-occurring tertiary structure elements, and were selected on the basis of two criteria. First, in order to measure the effect of various concentrations of TMAO and KCl on the RNA stability, the tertiary folding transition had to be resolvable in the UV melting profile of each RNA. Second, the RNAs were chosen to demonstrate a range of folding strategies as suggested by differences in their structural complexity, their ionic requirements for folding, and the degree to which the phosphate backbone is solvent-inaccessible in the native structure. Three of the RNAs adopt native structures under moderate monovalent salt conditions in the absence of Mg2+: the tar-tar* kissing loop is a small complex of two RNA hairpins (Figure 1B);26 a homodimeric tetraloop-receptor complex (TLR RNA) reproduces a common tertiary structural motif (Figure 1E)27; 28 and is selectively stabilized by K+ binding at a chelation site;29 and the aptamer domain of the A-riboswitch contains two sets of tertiary interactions (Figure 1D),30; 31 one of which is formed around a purine ligand. The fourth RNA, a 58 nucleotide fragment of ribosomal RNA (58mer RNA, Figure 1C) is stabilized by chelation of both K+ and Mg2+ and strongly dependent on Mg2+ for stability.32; 33 This rRNA fragment is also the most compact RNA in this study, in the sense that it exposes less surface area to solvent (per nucleotide) than any of the others.12
Figure 1.
Schematics of the secondary and tertiary structures of the RNAs used in this study. Horizontal black bars and bullets represent Watson-Crick and non-canonical base pairs, respectively. Gray lines symbolize base-base tertiary interactions and black lines with arrow-heads represent 5’-3’ backbone connectivity. (a) A designed hairpin. (b) The tar-tar* kissing-loops complex. (c) Nucleotides 1051–1108 of the E. coli 16S rRNA, with a mutation (U1061A) that stabilizes tertiary structure 37 (58mer RNA). (d) The aptamer domain of the adenine-binding riboswitch with adenine ligand depicted in outline typeface (A-riboswitch). (e) The tetraloop-receptor RNA (TLR).
TMAO and salt dependences of folding four RNAs
We used UV melting profiles to follow the effects of TMAO on RNA stability 12 (see Materials and Methods for details). To allow for the possibility of synergistic or antagonistic effects between salt and TMAO, melting experiments were performed in the presence of increasing KCl molality at various fixed TMAO concentrations (Figure 2, and see Supplementary Information). To keep the analysis confined to a two-dimensional matrix of salt vs. TMAO concentrations, Mg2+ has not been included in any of these experiments. Four of the RNAs in Figure 1 were investigated this way. More extreme TMAO and salt concentrations are needed to fold the 58mer rRNA in the absence of Mg2+; it is considered separately below.
Figure 2.
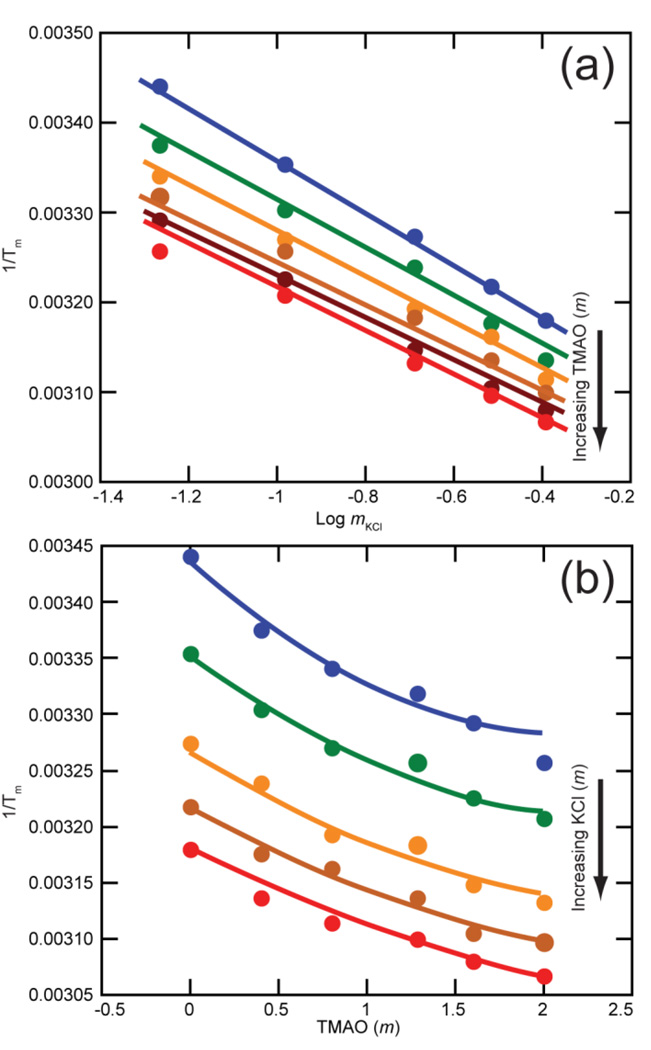
Salt and TMAO dependences of tertiary structure stability of the A-riboswitch aptamer domain, plotted as (1/Tm) obtained from melting experiments. The two panels show the same set of 30 different conditions. The drawn curves are least squares best fits all derived from the same three dimensional surface specified by six fitting parameters (see Materials and Methods). (a) KCl dependence at fixed TMAO concentrations: blue, no TMAO; green, 0.4 m; orange, 0.8 m; brown, 1.284 m, dark brown, 1.6 m; red, 2.0 m. (b) Data from panel A replotted to show TMAO dependence at fixed K+ concentrations: blue, 54 mm; green, 104 mm; orange, 204 mm; brown, 304 mm; red, 404 mm. Each melt sample contained 50 mm KMOPS pH 7.0, 5 µm DAP and 2 µm EDTA along with additional KCl and TMAO to give the indicated concentrations. Errors bars are smaller than the size of data points.
After extracting the melting temperature (Tm) of the first (tertiary) melting transition from the melting profiles, data for the A-riboswitch show a typical semi-logarithmic dependence of (1/Tm) on the KCl molality (Figure 2A). The dependence of (1/Tm) on TMAO molality is best described by a second order polynomial (Figure 2B), with higher TMAO concentrations being proportionately less stabilizing, per molal of osmolyte. The entire TMAO-salt data set was globally fit to one set of six parameters (see Materials and Methods). In the analysis that follows, (1/Tm) was transformed into ln(Kobs) using an average ΔH° of folding obtained by analysis of the melting curves (Table 1; see Materials and Methods). Kobs is the observed equilibrium constant for an unfolding transition; therefore ln(Kobs) decreases as an RNA becomes more stable. In the limit of low TMAO concentrations, three empirical quantities derived from the parameter set are of interest (Table 1): the dependence of ln(Kobs) on salt concentration in the absence of TMAO, called SKobs (eq 3); the dependence of ln(Kobs) on TMAO molality at a fixed 200 mm KCl concentration, [∂ln(Kobs)/∂mTMAO]mKCl; and an interaction term that gives the effect of TMAO (in the limit of low concentrations) on SKobs. Results for the tar-tar* and TLR RNAs (Supplementary Information Figure S1) were qualitatively similar to those shown for the A-riboswitch ; all three of these RNAs are stabilized by TMAO (Table 1). TMAO had only a slight destabilizing effect on the hairpin, and the salt dependence of the hairpin stability was virtually unaffected by TMAO (Table 1).
Table 1.
Parameters for KCl and TMAO effects on RNA unfolding reactionsa
| RNA: | Hairpin | A-riboswitch | tar-tar* | TLR | units |
|---|---|---|---|---|---|
| SKobsb | −0.59 ± 0.08 | −4.03 ± 0.49 | −2.13 ± 0.19 | −3.99 ± 0.40 | - |
| (∂lnKobs/∂mTMAO)mKClc | 0.09 ± 0.06 | −3.12 ± 0.41 | −1.19 ± 0.14 | −2.47 ± 0.27 | m−1 |
| Salt-osmolyte interactiond | - | 0.90 ± 0.13 | 0.38 ± 0.06 | 1.00 ±0.11 | m−1 |
| ΔH°e | 54.7 ± 3.9 | 63.2 ± 7.7 | 29.2 ± 2.6 | 30.0 ± 3.0 | kcal/mol |
| 2ΔΓ±f | −0.66 ± 0.08 | −4.50 ± 0.55 | −2.38 ± 0.21 | −4.47 ± 0.45 | ions per RNA |
| (∂ΔG°/∂mTMAO)aKClg (m-value) | −0.05 ± 0.04 | 1.85 ± 0.25 | 0.70 ± 0.08 | 1.46 ± 0.16 | kcal/mol/m |
| ΔB1h | −5 ± 3 | 173 ± 23 | 66 ± 8 | 137 ± 15 | H2O per RNA |
The first three rows of tabulated parameters were derived from sets of Tm values derived from melting curves done in a matrix of KCl and TMAO concentrations. The hairpin RNA parameters were obtained by linear least squares fitting at various fixed TMAO concentrations and the assumption of a zero salt-osmolyte interaction term; data sets for the other RNAs were globally fit to a single equation. See Materials and Methods for further details. Errors include the error associated with the global fit analysis and the uncertainty in ΔH°.
∂ln(Kobs)/∂ln(mKCl) evaluated in the absence of TMAO (coefficient a0 multiplied by (ΔH°/R), see eq 12 of Materials and Methods).
Derivative evaluated at 200 mm KCl in the limit of zero TMAO (eq 14).
Coefficient a1 multiplied by (ΔH°/R); see eq 12 and Materials and Methods.
Unfolding transition ΔH° and the associated error were obtained by averaging values returned in fitting two-state transitions to melting profiles (see Materials and Methods); the exception is the TLR RNA, for which ΔH° from scanning calorimetry experiments was previously reported.12
Derived from SKobs by eq 3.
Dependence of the folding free energy on TMAO molality at constant KCl activity in the limit of low TMAO concentration, called the m-value in the text (see eq 4 and 5).
ΔB1 is the minimum number of water molecules that become inaccessible to TMAO upon unfolding of the RNA (eq 7).
Two thermodynamic quantities listed in Table 1 are derived from the empirical parameters and describe the sensitivity of the RNA folding reaction to either salt or TMAO. One is 2ΔΓ±, the number of ions released upon unfolding (eq 3) in the absence of TMAO. The other quantity, (∂ΔG°obs/∂mTMAO)aKCl, is similar to the “m-value” standardly used to characterize the effects of osmolytes on protein folding (see Background, eq 5b), but differs in being expressed in molal instead of molar concentration units. In calculating the m-value, an additive correction term is needed to transform the TMAO dependence of the RNA stability measured at constant KCl concentration to the same dependence taken at constant KCl activity (eq 5). Measurement of the TMAO – KCl interaction energy necessary to calculate this correction is considered below; the term makes a negligibly small contribution to the reported m-values, on the order of 0.001 kcal/mol/m. (About 10% of the reported m-value errors reported in Table 1 comes from estimated errors in the measurement of the TMAO – KCl interaction energy.) The m-values we measure are qualitatively different between the hairpin secondary structure (~ 0 kcal/mol/m) and the RNAs with tertiary structure (0.70 to 1.85 kcal/mol/m, Table 1). For comparison, some molar m-values for TMAO stabilization of proteins are 1.64 kcal/mol/m (reduced ribonuclease A, 124 residues) and 2.37 kcal/mol/m (staphylococcal nuclease, 149 residues).10 On a per residue basis, TMAO is a more effective stabilizer of RNAs than proteins.
In all three RNAs with tertiary structure, the positive salt – TMAO interaction factor (Table 1) means that TMAO concentration reduces the magnitude of ion release (2ΔΓ±). We attribute this reduction to an effect of TMAO on the extension of the partially unfolded RNA in solution, bringing it closer to the native state charge density (see Discussion). Lastly, the estimated number of solvating water molecules that are taken up when the RNA unfolds is derived from the limiting value of ∂ln(Kobs)/∂mTMAO by eq 7 (Table 1). The calculation assumes that TMAO is strongly excluded from these waters, a point which is considered in the Discussion.
Isothermal determination of the A-riboswitch m-value
The derivation of the thermodynamic parameters in Table 1 from Tm data assumes the parameters are temperature independent. The ΔH° values for RNA unfolding derived from the melting profiles do not show any trend with Tm or TMAO concentration, within error, but the possibility remains that TMAO could become a more (or less) effective stabilizer at higher temperatures. For the A-riboswitch, we found salt (50 mm K+) and ligand (10 µm adenine) concentrations at which the RNA is predominantly in the unfolded form, but folds to the native structure upon titration with TMAO at constant temperature (22.5 °C) (Materials and Methods and Supplementary Figure S2). The m-value (0.69 ± 0.04 kcal/mol/m) at the midpoint of the titration (1.47 ± 0.31 m TMAO) was determined by standard methods.19 (The large error in the midpoint comes from uncertainties in baselines over the accessible range of TMAO concentrations.) From the global fit analysis of Tm data (Figure 2), the m-value at the same salt and TMAO concentrations is 0.92 ± 0.36 kcal/mol/m, which is higher than the isothermally-determined value but within experimental error. The overall range of Tm data used in the global fit analysis is 17 – 54 °C, though the interpolated m-value for 50 mm K+ and 1.47 m TMAO is most strongly affected by Tms near 30 °C. We conclude that the m-values compiled in Table 1 are not very strongly biased by temperature effects, though it is still possible that m-values vary significantly over the full temperature range covered by the data in Figure 2.
TMAO dependence of 58mer RNA stability
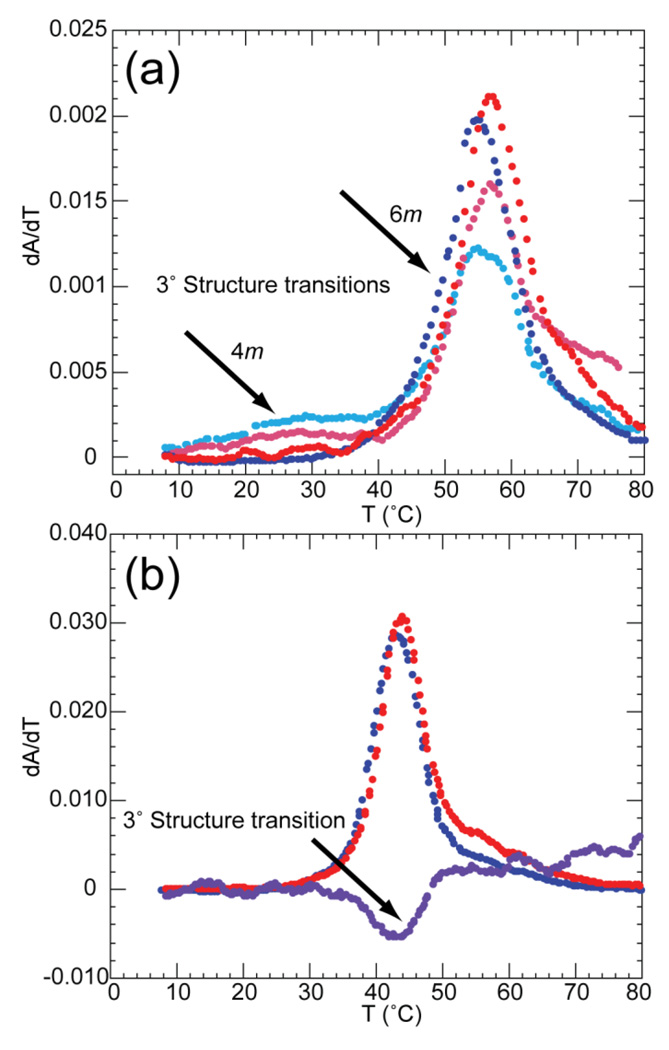
Among the RNAs in Figure 1, the 58mer rRNA fragment (Figure 1C) is unique in having a chelated Mg2+ buried within its structure.34 In the absence of Mg2+, the RNA folds only under extreme conditions, e.g. 1.6 M NH4Cl.35; 36 We find that high concentrations of TMAO can substitute for Mg2+ in promoting the native 58mer RNA structure (Figure 3). The tertiary unfolding transition in this RNA is characterized by an increase in absorbance at 260 nm, a minimal change at 280 nm, and a decrease at 295 nm.33; 37 In 400 mm K+ and 4 m TMAO, the tertiary structure unfolding is apparent as a resolved transition at ~30 °C (Figure 3A). Raising the TMAO concentration to 6 m simultaneously raises the Tm of the tertiary transition and decreases the stability of the higher temperature secondary structure transitions. The tertiary structure no longer unfolds as a distinct transition, though the small displacement of the peaks at 260 and 280 nm indicates that tertiary unfolding precedes subsequent unfolding steps. At higher concentrations of TMAO, most of the RNA unfolds in a single transition (Figure 3B); the presence of a hypochromic change at 295 nm confirms the existence of the tertiary structure under these conditions (7.7 m TMAO, 52.4 mm K+). As the K+ concentration is raised, less TMAO is needed to induce formation of the tertiary structure; e.g., at 1 m K+ only ~3 m TMAO is needed to see the tertiary unfolding transition (Tm ~35 °C, data not shown).
Figure 3.
Melt profiles of 58mer RNA in various TMAO and salt concentrations. A) Data sets were collected at 260 (blue) and 280 (red) nm in buffer containing 400 mm K+, 2 µm EDTA and either 100 mm K-MOPS pH 6.8 with 4 m TMAO (light shades), or 160 mm K-MOPS pH 6.8 and 6 m TMAO (dark shades). B) Data were collected at 260 (blue), 280 (red), and 295 (purple) nm in the presence of 52.4 mm K+, 2 µm EDTA, 182 mm K-MOPS and 7.7 m TMAO. Arrows indicate the change in ratio of absorbance at 260/280nm (A) or 295nm signal (B) corresponding to melting of tertiary structure.
By assuming that the enthalpies of the unfolding transitions do not change with salt or osmolyte concentration, we extracted ΔG° for tertiary structure unfolding from melting data obtained between 4 and 6 m TMAO (see Materials and Methods). At a constant 400 mm K+, ∂ΔG°/∂mTMAO for RNA unfolding is approximately 1.1 kcal/mol/m; at 600 mm K+, it is 1.4 kcal/mol/m. These “m-values” are not exactly the same as the free energy derivative reported for the other RNAs in Table 1, as they have not been extrapolated to the limit of low TMAO concentrations. Because we have seen with other RNAs that higher concentrations of TMAO tend to be less effective on a per molal basis, these numbers may underestimate the magnitude of the osmolyte stabilizing effect with the 58mer RNA.
TMAO-solute interactions
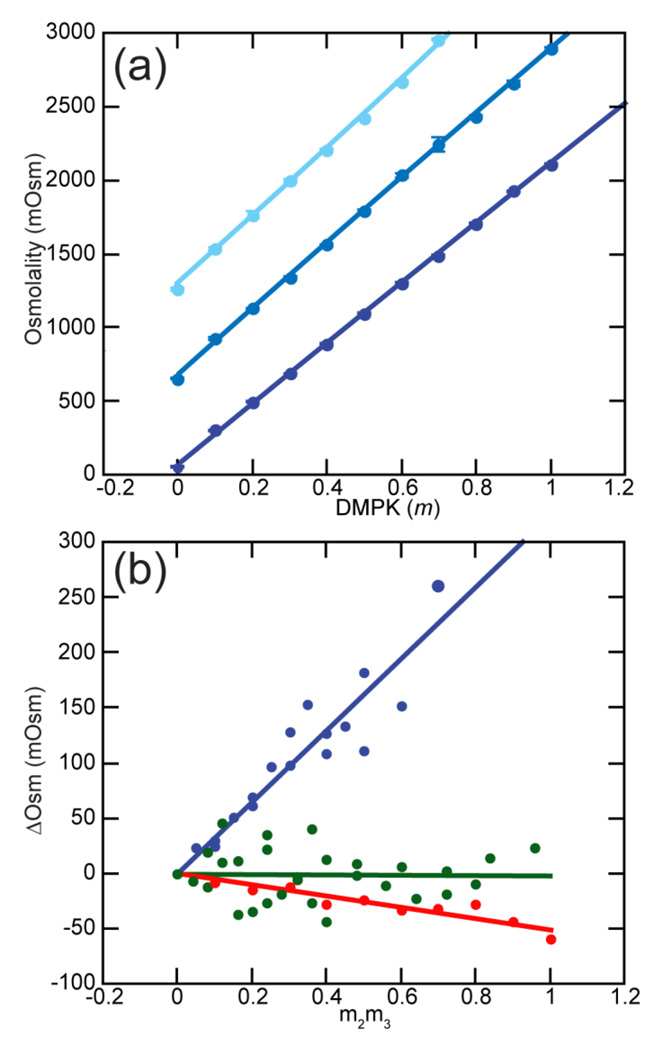
To ask if the observed stabilizing effect of TMAO on RNA tertiary structures can be interpreted in terms of TMAO interactions with specific groups, we used VPO to measure the interactions between TMAO and several small molecules mimicking RNA bases, ribose sugar, or phosphate backbone. The methodology is described in the Background section and developed in detail elsewhere (see 24 and references therein). Figure 4A shows typical VPO data obtained with the potassium salt of dimethylphosphate (K-DMP), which was synthesized to reproduce an isolated phosphodiester of the RNA backbone (see Materials and Methods). The VPO instrument reports the osmolality of a solution, which is the concentration of an ideal solute that would be required to produce the observed water vapor pressure. For K-DMP, there is a nearly linear dependence of the osmolality on the actual solution molality (Figure 4A). When TMAO is included the slope of the plot becomes slightly steeper, which indicates a repulsive (unfavorable) interaction between TMAO and the K-DMP ions; that is, TMAO and K-DMP interact more strongly with water than with each other. A convenient way to show these small differences and quantify the strength of the interaction is the plot in Figure 4B; the slope of the plot is the quantity μ23/RT as defined in eq 10 (Table 2). The interaction free energy between TMAO and K-DMP is given by the related quantity , the excess chemical potential derivative (eq 11). TMAO is found to have a strongly unfavorable interaction with K-DMP, 211 cal/mol/m (Table 2). This positive free energy is especially notable in comparison to the weak overall interactions of TMAO with KCl (Table 2 and see below). TMAO must have a much more unfavorable interaction with the DMP− anion than with Cl−.
Figure 4.
Vapor Pressure Osmometry (VPO) measurements and analysis. (a) Osmolality of potassium dimethylphosphate (K-DMP) with (from bottom to top) 0, 0.5, or 1.0 m TMAO. Fitted curves are second order polynomials. Error bars are shown, but are generally smaller than the data points. (b) The non-additivity of TMAO and solute osmolalities (ΔOsm) plotted according to eqs 7–8. Lines are linear least squares fits; the slopes are reported in Table 3 as μ23/RT. Blue, TMAO and K-DMAP; green, TMAO and KCl; red, TMAO and glycerol.
Table 2.
TMAO-solute interaction free energies
| Solute | μ23/RT, m−1 | , cal/mol/m (25 °C) |
|---|---|---|
| purine | 0.1425 ± 0.018 | 94.7 ± 10.6 |
| cytidine | 0.161 ± 0.024 | 106 ± 14 |
| uridine | 0.145 ± 0.017 | 96 ± 10 |
| glycerol | −0.0503 ± 0.0072 | −17.3 ± 4.2 |
| Potassium dimethylphosphate | 0.322 ± 0.027 | 211 ± 16 |
| KCl | −0.0018 ± 0.015 | - |
| amino acid side chain | ΔGtransfer, cal/mol/mb | |
| Ala | −13.6 | |
| Leu | 10.8 | |
| Phe | −8.65 | |
| Trp | −141.8 | |
| Tyr | −106.0 | |
| His | 39.0 | |
| Arg | −101.4 |
μ23/RT is the slope of ΔOsm (eq 7) plotted as in Figure 4B. is calculated from μ23/RT at 25 °C and includes a correction for the ideal entropy of mixing. See Background (eq 7–9) and Materials and Methods for details.
Transfer free energies based on relative solubilities of amino acids in water and 1 M TMAO, taken from reference 8. The transfer free energy of glycine has been subtracted, so ΔGtransfer applies to the amino acid side chain. The partial molar volume of TMAO68 was used to transform ΔGtransfer from molar to molal units.
Additional VPO measurements were made with compounds representative of the base and sugar components of an RNA (Table 2). A base soluble enough for VPO measurements is purine, 38 which has a significant unfavorable interaction with TMAO. The nucleosides cytidine and uridine also show positive interaction free energies (Supplementary Data Figure S3). Lastly, glycerol was examined as a model for TMAO interactions with the ribose sugar; it has small but favorable interactions with TMAO (Table 2 and Figure 4B).
For comparison, free energies for the transfer of amino acid side chains from water to 1 m TMAO, based on solubility measurements reported by Auton & Bolen,8 are included in Table 2. These free energies are similar to the chemical potential derivatives obtained from VPO experiments. Interactions with aliphatic and aromatic carbons are weak, but there are strongly favorable interactions with tryptophan and tyrosine side chains. All the data in Table 2 can be qualitatively rationalized by the assumptions that net favorable interactions take place between TMAO and hydrogen bond donors, while TMAO is strongly excluded (unfavorable, positive free energies) from the vicinity of hydrogen bond acceptors. For instance, tryptophan and tyrosine side chains and purine all have one hydrogen bond donor, but purine also has three hydrogen bond acceptors and thus a net unfavorable interaction with TMAO. The relation between this pattern of TMAO interactions and RNA helix stability is elaborated in the Discussion.
TMAO-KCl interactions are weak
RNA stability is strongly dependent upon the thermodynamic activity of salt present in solution; therefore, any interaction of TMAO with salt will shift the RNA folding equilibrium simply because of the change in salt activity. Based on VPO measurements (Figure 4A), μ23 for TMAO - KCl interactions is not significantly different from zero (Table 2) and no correction need be made to (∂ΔGobs/∂mTMAO)mKCl to obtain the m-value (eq 5b). This result is consistent with the weak interactions measured between glycine betaine, an osmolyte that is chemically similar to TMAO, and KCl (28.4 cal/mol/m) or NaCl (−43.8 cal/mol/m).24 We conclude that essentially all the effects of TMAO on RNA stability that we measure (Table 1) originate from favorable and unfavorable interactions of the osmolyte with the RNA.
TMAO reduces the overall dimensions of partially unfolded RNAs
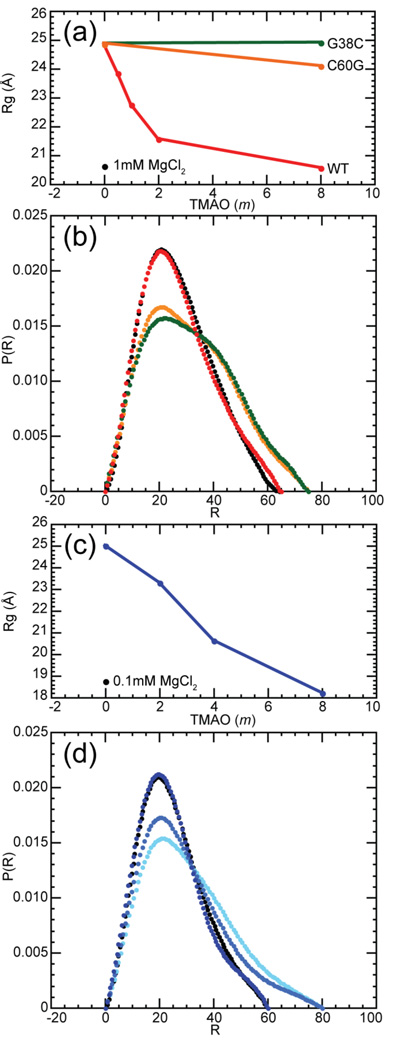
Protecting osmolytes such as TMAO reduce the radius of gyration (Rg) of denatured proteins.39 The Rg of the ensemble of RNA structures from which folding takes place is also sensitive to solvent conditions, notably to the concentration of Mg2+ but also to monovalent ions.40; 41; 42; 43; 44 To determine whether TMAO also affects the overall dimensions of partially folded RNAs, small angle X-ray scattering (SAXS) measurements were made on two of the RNAs in Figure 1, the A-riboswitch and the 58mer rRNA fragment. In the absence of TMAO, the Rg of the A-riboswitch is nearly 25 Å. Increases in TMAO concentrations reduce Rg to 20.6 Å, nearly the same radius as observed when 1 mM MgCl2 is added under the same buffer conditions (50 mM K+, Figure 5A) and close to the Rg calculated from the A-riboswitch crystal structure (20.3 Å). (Because scattering measurements were made in the absence of ligand, the compact A-riboswitch structures we observe cannot have the native conformation of the purine binding pocket. The tertiary contacts between the two hairpin loops nevertheless form when millimolar concentrations of Mg2+ are present.31) Two A-riboswitch variants were also assayed, G38C and C60G (see sequence in Figure 1D). These mutations disrupt the formation of a base pair between the hairpin loops and strongly destabilize the tertiary structure (reference 45 and unpublished data). In the absence of the osmolyte, these two variants display radii of gyration identical to that of the wild-type RNA (25 Å), but even at 8 m TMAO their radii are unchanged (G38C) or only slightly reduced (C60G). Thus, it appears that TMAO only reduces the dimensions of the A-riboswitch RNA if the correct tertiary structure can form. TMAO also reduces the dimensions of the 58mer rRNA fragment from around 25 Å to 18.2 Å, a radius similar to the one observed in the presence of 100 µm Mg2+ in the same buffer (60 mm K+) (Figure 5B).
Figure 5.
Dimensions of A-riboswitch and 58mer RNAs at various TMAO and Mg2+ concentrations, as determined by SAXS. (a) Rg of the A-riboswitch wildtype sequence (red) and two folding-impaired variants, C60G (orange) and G28C (green), in 182 mm KMOPS pH 6.8, 2 µm EDTA, 50 mm K+, and various molalities of TMAO. For comparison purposes, Rg in the same buffer containing 1 mM Mg2+ (black point) is also indicated. (b) Distance distribution functions of the A-riboswitch with 8 m TMAO (red) or 1mm Mg2+ (black), and of the G38C (green) and C60G variants (orange) with 8 m TMAO. Other buffer components are the same as in panel (a). (c) Rg of the 58mer RNA (blue) in 182 mm MOPS pH 6.8, 2 µm EDTA, 50 mm K+, and various molalities of TMAO. For comparison purposes, Rg in the same buffer containing 0.1mm Mg2+ (black) is also indicated. In both panels (a) and (c), error bars are smaller than the size of the data points. (d) Distance distribution function of the 58mer rRNA in 2 m TMAO (light blue), 4 m TMAO (medium blue), 8 m (dark blue), and 0.1 mm Mg2+ (black). Other buffer components are the same as in panel (c).
The distance distribution profile derived from the scattering profile contains more information about the shape of the RNAs than Rg, which is derived from only the smallest scattering angles. The wild-type A-riboswitch profiles are very similar whether a compact form was induced by the presence of TMAO or Mg2+; the variant sequences show a broader distribution of distances (Figure 5C and Supplementary Data Figure S4). Similarly, the 58mer rRNA structures stabilized by 8 m TMAO or 100 µM Mg2+ are nearly indistinguishable (Figure 5D).
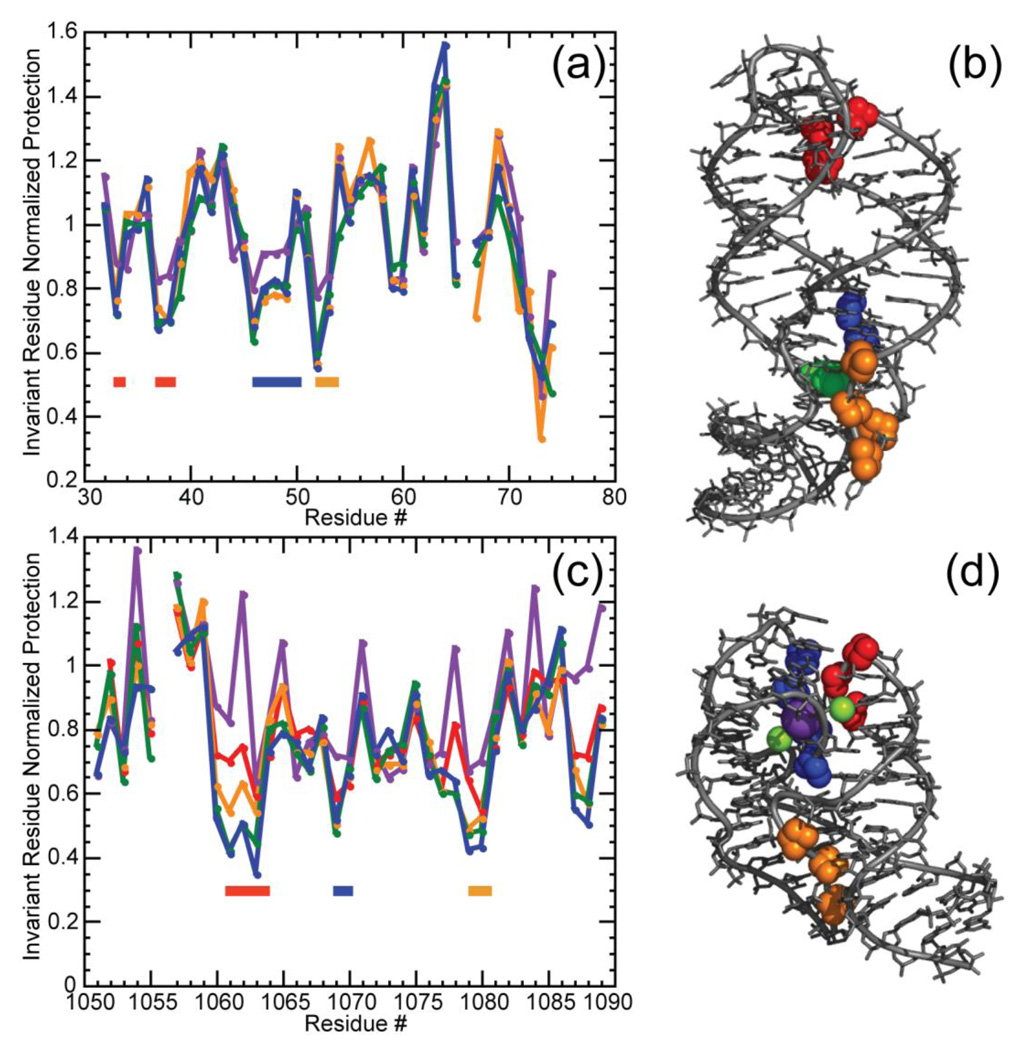
Hydroxyl radical probing of TMAO-stabilized tertiary structures
To further compare the Mg2+- and TMAO-stabilized structures of the A-riboswitch and 58mer RNAs, we probed the accessibility of the backbone to hydroxyl radical. This free radical reacts with DNA and RNA sugars and serves as a probe of solvent accessibility to the backbone at nucleotide resolution; tertiary structure formation is usually associated with reduced ribose reactivity.46; 47 In the case of the A-riboswitch, sugars at positions associated with the interacting hairpin loops (33, 37, 38) and the adenine binding pocket (46–49, 52 and 53) all become similarly protected from reaction upon addition of either 5 mm Mg2+ or 8 m TMAO; 5 m TMAO is almost identically effective (Figure 6A, B). (Because ligand was not included in these experiments, the organization of the binding pocket region may not be the same as observed in the crystal structure.) In a similar way, the 58mer rRNA fragment shows protection of a number of riboses associated with tertiary structure (18–21, 35–37, 45–47) (Figure 6C, D). There is a clear trend of increasing protection as a function of TMAO concentration (most easily observable for residues 18–21); an essentially identical reactivity pattern is seen with either 8 m TMAO or 5 mm Mg2+ (60 mm K+).
Figure 6.
Normalized data for the reactivity of the A-riboswitch (a, b) and 58mer rRNA fragment (c, d) towards hydroxyl radical. Gel band intensities have been normalized as described (Materials and Methods). (a) Reactivity of the A-riboswitch was assayed in K-MOPS buffer pH 6.8, 50 mm K+ plus no TMAO (purple); 5 m TMAO (yellow); 8 m TMAO (green) or 5 mm MgCl2 (blue). MOPS anion concentrations were 20 mm (no TMAO or MgCl2), 125 mm (5 m TMAO) or 182 mm (8 m TMAO). Regions of increased protection compared to the unfolded conformation are indicated by colored bars corresponding to residues depicted in panel (b). (b) Residues protected from hydroxyl radical displayed on the A-riboswitch crystal structure (1Y26) where residues 33, 37 and 38 are colored in red, 46 to 49 are displayed in blue, and 52 and 53 are shown in yellow. The adenine ligand is depicted in green. (c) Reactivity of the 58mer RNA obtained in K-MOPS buffer pH 6.8, 60 mM K+ plus no TMAO (purple); 4 m TMAO (red), 5 m TMAO (yellow), 8m TMAO (green); or 5 mm MgCl2 (blue). MOPS anion concentrations were 20 mm (no TMAO or MgCl2), 100 mm (4 m TMAO) 125 mm (5 m TMAO) or 182 mm (8 m TMAO). Regions of increased protection compared to the unfolded conformation are indicated by colored bars corresponding to residues depicted in panel (d). (d) Representation of residues protected from hydroxyl radical on the 58mer rRNA crystal structure (1HC8) where residues 18 to 21 are colored in red, 35 to 37 are depicted in blue and 45 to 47 are indicated in yellow. Residues 14 in the 58mer and 66 in the A-riboswitch were impossible to quantify accurately and were not plotted. Protection assessments for residues at the 3’end, which correspond nucleotides at the bottom of the gel, were also unreliable.
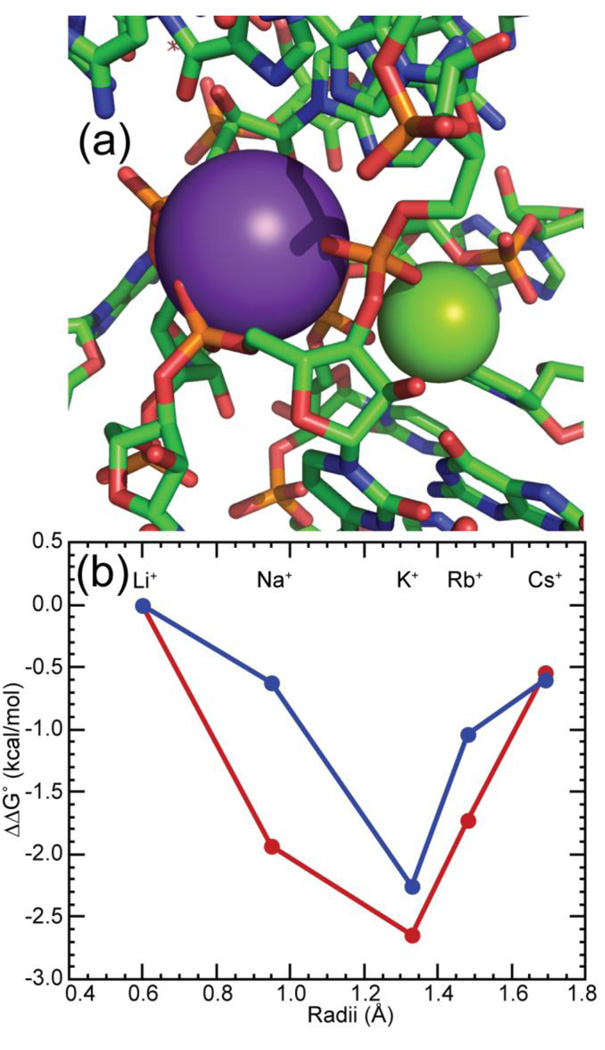
Monovalent ion specificity of 58mer RNA folding
The 58mer RNA is selectively stabilized by K+ in preference to larger or smaller group I ions,36 most likely reflecting the specificity of the K+ chelation site seen in the crystal structure (Figure 7A).32 The binding pocket for this ion is part of an unusual tertiary structure in which four phosphates are turned towards the RNA interior and line cavities containing chelated Mg2+ and K+ ions; A1073 contributes one anionic oxygen to each chelation site. Thus it was of interest to know whether the monovalent ion specificity would persist when the tertiary structure is stabilized by TMAO, or whether the lack of a chelated Mg2+ would cause a rearrangement of the buried phosphates. We observe a similar preference for K+ over most other group I ions, whether the structure is stabilized by TMAO or by Mg2+ (Figure 7B). (Na+ is significantly more effective with the TMAO-stabilized structure; perhaps the ion is able to bind specifically in or near the Mg2+ chelation site.) This result is consistent with the same protection of A1073 from hydroxyl radical reaction in either TMAO- or Mg2+- stabilized RNAs.
Figure 7.
The 58mer RNA ion-binding pocket confers a specific monovalent ion requirement for optimal stability. (a) View of the crystal structure of the 58mer RNA (1HC8) regions surrounding chelated K+ (violet sphere) and Mg2+ (green sphere) ions. Anionic oxygens of A1073 contact either the K+ or Mg2+ ion. (b) Relative free energy changes for folding the 58mer rRNA fragment with either 0.5 mM MgCl2 (blue) or 6 m TMAO (red) added to buffer with different group I ions (1 m M+, 150 mm M-MOPS pH 6.8, 2 µm EDTA). The ionic radii are taken from Pauling.69
DISCUSSION
Effects of TMAO on RNA structure and stability
TMAO is an effective stabilizer of protein native structure;6; 9 it also favors more compact (smaller Rg) conformations of unfolded proteins.39 In this work, we find that TMAO has similar effects on RNAs with tertiary structure. Before discussing these effects, we note an important control observation: the activity of KCl is negligibly perturbed by TMAO (Table 2). Therefore, the effects of TMAO on RNA stability are not an indirect effect of changes in the “effective concentration” (thermodynamic activity) of the salt, and we do not expect TMAO to alter the distribution of monovalent ions around an RNA. With this convenient simplification in mind, we consider three aspects of the effects of TMAO on RNA structure and stability.
First, we confirmed our previous observation12 that TMAO perturbs the stability of RNA secondary structure to only a small degree. The Tm of a synthetic hairpin was nearly unaffected by TMAO (Table 1), and slight destabilization of secondary structure transitions was seen in all of the RNAs tested (e.g., Figure 3). We attribute this lack of effect to a fortuitous cancellation of favorable and unfavorable interactions, primarily with base hydrogen bond acceptors and donors. TMAO is a very polar molecule and should be a good hydrogen bond acceptor;48 it is therefore unsurprising that hydrogen bond donors (e.g. glycerol, Table 2) have some preference for interacting with TMAO over water. Conversely, TMAO is incapable of donating a hydrogen bond and should not compete well with water for hydrogen bond acceptors such as uridine carbonyls. Although other factors undoubtedly contribute, we suppose that a major reason for the net exclusion of TMAO from purine and the nucleosides we tested is the presence of more hydrogen bond acceptors than donors on the bases. Detailed studies of glycine betaine, another trimethylamine protecting osmolyte, have similarly found a favorable interaction of the compound with hydrogen bond donors (e.g., amide nitrogen) and unfavorable interaction with hydrogen bond acceptors (e.g., amide oxygen).24 (The balance of favorable and unfavorable interactions is such that glycine betaine destabilizes RNA secondary structure.12; 49) Denaturation of an RNA duplex to single strands is accompanied by the exposure of equal numbers of base hydrogen bond acceptors and donors to solvent. We hypothesize that favorable TMAO interactions with base hydrogen bond acceptors are approximately canceled by unfavorable interactions with hydrogen bond donors, leaving RNA duplex stability nearly unaffected.
Hydrogen bond surfaces exposed upon unfolding of tertiary structures may include ribose 2' OH as well as base acceptors and donors. The rather weak, favorable interaction of TMAO with hydroxyl (glycerol, Table 2) may not cancel the strongly unfavorable interactions that probably take place with base hydrogen bond acceptors. However, exposure of 2' OH to solvent is unlikely to account for the effects of TMAO on the tertiary structures examined here. The TLR motif, for example, has a single 2' OH hydrogen bonded to a donor N1 and acceptor N6 of two adenine bases. Exposure of these three hydrogen bonding groups to TMAO should have little net effect on the stability of the RNA, and certainly cannot account for the m-value we observe.
Second, TMAO reduces the dimensions of partially unfolded RNAs. X-ray scattering experiments show that the average Rg of the unfolded form of either the A-riboswitch or 58mer RNAs is gradually reduced as TMAO is added, until the RNA has nearly the same dimensions as seen with Mg2+ present. This observation is consistent with the finding that the unfolding reaction becomes less salt dependent (fewer ions are released) as TMAO is added (Table 1, the salt-TMAO interaction factor is positive). The less extended the unfolded state, the closer it is in charge density to the native conformation and the smaller the overall uptake of ions upon folding. The lack of any effect of TMAO on the average extension of mutant RNAs unable to form the native tertiary structure shows that TMAO does not indiscriminately restrict the RNA to more compact conformations. Instead, the data suggest that the RNA transiently samples conformations with native tertiary contacts, and that TMAO shifts the distribution of conformations towards ones with native-like structures. In a similar way, Mg2+ promotes more compact conformations of the A-riboswitch RNA, but has little effect on the dimensions of the C60G or G38C mutants (D. Leipply & D.E.D., unpublished data).
Third, TMAO stabilizes the correct RNA tertiary structure. By two criteria, the native structures stabilized by TMAO are the same as those observed in the presence of Mg2+: the distance distribution profiles from SAXS experiments are essentially identical whether the structure has been stabilized by TMAO or Mg2+ (Figure 5), and hydroxyl radical probing gives the same pattern of nucleotide reactivity (Figure 6).
TMAO exclusion from RNA phosphates and changes in RNA hydration
The propensity of TMAO to stabilize native protein structures has been attributed to the strong exclusion of TMAO from the peptide backbone (83.5 cal/mol/m), which favors the burial of peptides in the protein interior over their exposure to solvent.8 The even stronger exclusion of TMAO from backbone phosphate (211 cal/mol/m, Table 2) suggests that a similar mechanism could be at work in RNA: the energetic cost of phosphate desolvation is reduced when TMAO is part of the solvent. We argue that this mechanism is the only plausible way TMAO could be stabilizing RNA tertiary structures: as pointed out in the above section, the net interactions of TMAO with base surfaces must change very little when RNA structures form, and we find no suggestion of strong TMAO interactions with backbone sugars (Table 2). If TMAO – phosphate interactions drive the RNA stabilizations we measure, to what extent must phosphate hydration be changing?
The unfolding of an RNA tertiary structure increases the volume of water from which TMAO is excluded (both ∂lnKobs/∂mTMAO, Table 1, and ΔΓTMAO, eq 5, are negative). The value of ΔΓTMAO sets a lower limit on the uptake of water that accompanies RNA unfolding, which is listed in Table 1 as ΔB1 (see eq 7); it ranges from 66 to 173 waters per RNA. Based on the above argument about the stabilization of RNA tertiary structure by TMAO exclusion from phosphate, we suggest that these ΔB1 values primarily report the increase in phosphate hydration that accompanies disruption of RNA tertiary structure. Though ΔB1 is nominally a lower limit on water uptake, it will be close to the actual value if TMAO is completely excluded from the water of hydration. It is reasonable to assume that this is the case. TMAO exclusion from phosphate anionic oxygen is comparable to that of the related osmolyte glycine betaine, for which measurements with double stranded DNA50 and phosphate24 are consistent with complete exclusion. The same measurements imply that a hydration layer two to three water molecules thick around anionic oxygens, or about 17 water molecules per nucleotide of duplex DNA, is inaccessible to the osmolyte. Using this number as a guide to what might be expected for phosphate hydration at the surfaces of partially unfolded RNAs, the three RNAs with tertiary structure in Table 1 have totals of 510 to 1462 hydrating waters, which are reduced by 10 – 15% by tertiary structure formation. Because some fraction of the nucleotides in these RNAs are in helical segments that are unperturbed by tertiary structure formation (e.g., the stems of the tar and tar* hairpins), some phosphates must be much more extensively dehydrated than this average value. Our results therefore imply that significant changes in phosphate hydration accompany RNA tertiary structure formation.
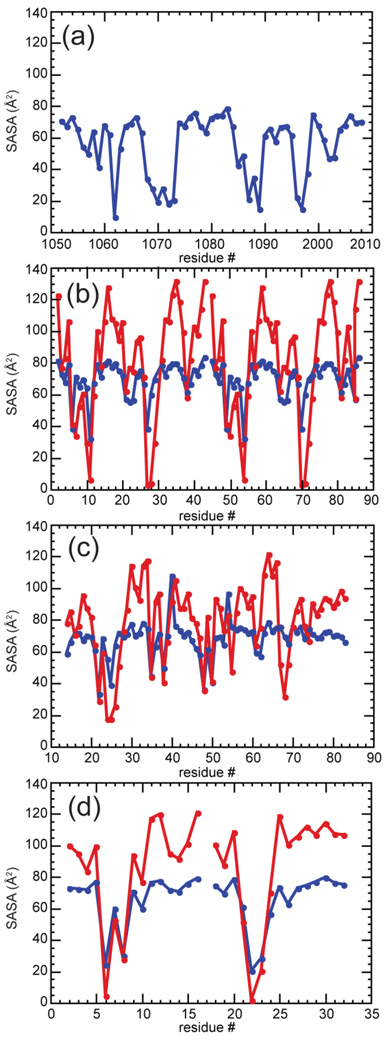
Solvent accessibility of phosphates in RNA tertiary structures
As a another way to evaluate phosphate hydration in RNA tertiary structures, we have calculated the solvent-accessible surface area (SASA) of backbone phosphates (the sum of anionic oxygens and phosphorus, excluding ester oxygen) for each RNA by standard methods (see Materials and Methods; total surface areas are listed in Table 3 and plots of individual residues are shown in Figure 8). Following studies of the effects of TMAO and other osmolytes on protein folding and protein-DNA binding equilibria,8; 24 we ask whether the free energy of stabilization contributed by TMAO is proportional to the change in the phosphate SASA that accompanies folding. Based on our measurement of TMAO - K-DMP interactions and a value of 85 Å2 for the SASA of the DMP phosphorus and anionic oxygens, we estimate a proportionality factor of 2.48 cal/Å2/m to use in calculating an m-value from changes in phosphate SASA (Table 3). (This calculation assumes that TMAO interactions with both K+ and methyl groups are negligible.*)
Table 3.
Changes in phosphate SASA accompanying RNA unfoldinga
| RNA | PO2 SASA (native), Å2 |
PO2 SASA (unfolded), Å2 |
Δ(SASA), Å2 | estimated m-value, kcal/mol/m |
|---|---|---|---|---|
| 58mer RNA | 3136 | 3534–4007 | 398 or 871 | 0.99 or 2.16 |
| tar-tar* | 1968 | 1860 – 2108 | −92 or 141 | −0.23 or 0.35 |
| TLR | 758 (receptor) 388 (GAAA) | 722 (receptor) 391 (GAAA) | −67 | −0.17 |
| A-riboswitch | 4768 | 4401–4991 | −367 or 223 | −0.91 or 0.55 |
Solvent accessible surface areas of backbone phosphate (phosphorus and the two non-bridging oxygens) for native RNA structures were calculated from PDB files specified in the legend to Figure 8. For TLR RNA, surface areas corresponding to the receptor (nucleotides U5 – G9 and C34 – G39 for chain A; U48 – G52 and C77 – G82 for chain B) and the tetraloop hairpin (nucleotides G19 – C24 for chain A; G62 – C67 for chain B) are reported separately. The unfolded TLR RNA surface areas are derived from models as described in the text. Note that these numbers are for each subunit whereas the total change in SASA is for the complex. The values given for unfolded tar-tar*, A-riboswitch and 58mer RNA used the per-nucleotide SASA previously calculated for canonical A-form RNA (the smaller value) or single-stranded RNA.12 The contribution of phosphate exposure to the m-value for RNA unfolding in TMAO were calculated using the proportionality 2.48 cal/Å2/m.
Figure 8.
Solvent accessible surface areas (SASA) of phosphates groups for four RNAs with tertiary structure (Figure 1). (a) 58mer rRNA (1HC8), (b) the two monomers from the tetraloop-receptor RNA complex (2JYF), (c) A-riboswitch (1Y26), and (d) Tar-tar* (1KIS). Blue data points indicates SASA obtained with a probe radius of 1.4 Å whereas red points correspond to a probe radius of 2.8 Å.
Of the four RNA tertiary structures examined, only the 58mer shows dramatic (and nearly complete) burial of several phosphates, most of which contact chelated ions (Figure 8A). To estimate the change in solvent accessible phosphate surface area, we use average values for either single stranded or double helical RNA (previous computed in reference 12) as surface areas that should bracket the extent of phosphate exposure in an unfolded RNA. The range of calculated m-values (0.99 – 2.16 kcal/mol/m, Table 3) overlaps the range of the estimated m-values (1.1 to 1.4 kcal/mol/m, corresponding to 102 – 130 waters taken up). As previously mentioned, these estimates may underestimate the limiting sensitivity of the RNA to TMAO. Nevertheless, the extent of phosphate burial adequately rationalizes the m-value.
None of the other three RNAs shows enough burial of phosphate surface area to account for measured m-values using a proportionality based on model compound (K-DMP) interaction energies. The most egregious case is the TLR RNA, which docks a very stable hairpin structure, the GAAA tetraloop, with a receptor. Contacts between the two RNA segments consist entirely of hydrogen-bonding and stacking between bases with no involvement of the backbone.51; 52; 53 As the structure of the tetraloop probably does not change upon docking27 and the structure of the receptor in the absence of tetraloop is known from NMR studies,52 we have a good model for the undocked structure. There is actually a small decrease in phosphate exposure of the separate components compared to the complex, which predicts a negative m-value (Table 3). The calculated m-values for tar-tar* and A-riboswitch RNAs, based on single-strand and duplex models for the unfolded RNAs, also underestimate the measured m-values significantly.
We suspect that, in these three RNAs, the accessibility of phosphate to water is not a good measure of the extent of phosphate dehydration. Dimerization of the TLR RNA places two helices in close proximity (Figure 1E), where several phosphates come fairly close together (2.6 to 4.5 Å between anionic oxygens). If the water excluded to TMAO extends over a layer two to three molecules thick around phosphate anionic oxygens,24;50 then bringing two phosphates into a position in which they share hydrating water molecules must substantially decrease the volume of water that is excluded to TMAO. When a sphere twice the diameter of water is used as a more realistic assessment of solvent changes around phosphates, six phosphates now appear "inaccessible" (Figure 8B). With the A-riboswitch RNA, tertiary structure formation brings the backbones of two helical segments close together (nucleotides 26 with 68–69); a turn of the backbone in the adenine binding pocket brings two phosphate oxygens within 3.6 Å (nucleotides 21–22). These two regions are identified by their lack of accessibility to a 2.8 Å sphere (Figure 8C). The two backbones of the tar-tar* RNA also bring several phosphate oxygens less than a water molecule diameter apart (Figure 8D).26;54
From these examinations of RNA structures, it seems that tertiary structure formation is frequently accompanied by the formation of phosphate – water networks, in which adjacent phosphates might share an inner shell of water but lose outer shells. The isolated phosphate of K-DMP may not be an appropriate compound for modeling the energetics of TMAO exclusion from these kinds of networked structures. The one case in which we calculated a reasonable m-value based on SASA calculations, the 58mer RNA, is also an RNA in which several phosphates become completely buried and desolvated. In this situation, the exclusion of TMAO from K-DMP might be expected to reproduce the energetics of phosphate burial.
Lastly, we note a parallel between protein and RNA folding studies: both are limited by the availability of good models for the ensemble of unfolded or partially unfolded conformations from which folding takes place.55; 56 Among the RNAs discussed here, only for the TLR RNA do we have a good model based on experimental data.
Parallels between TMAO- and Mg2+-induced RNA folding
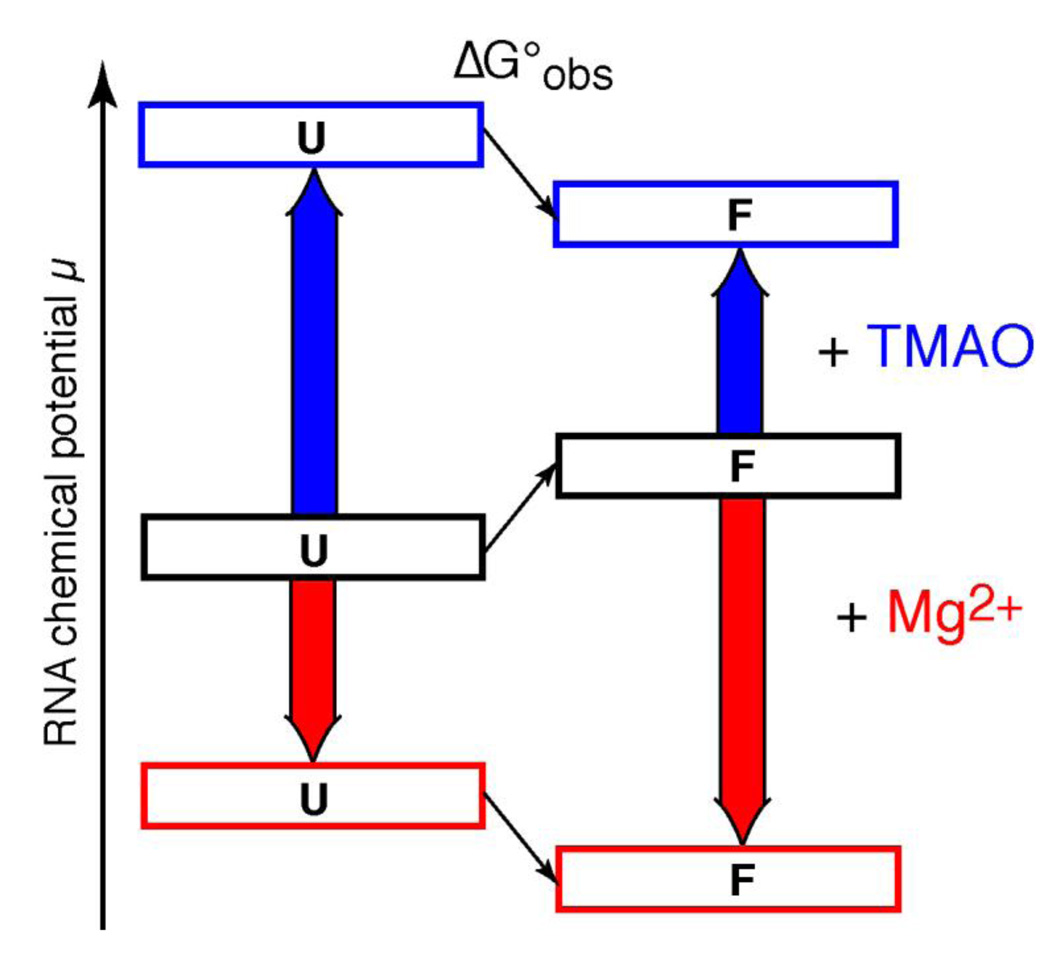
It is interesting to note that Mg2+ strongly influences RNA folding, with exactly the same outcomes as seen with TMAO: it favors compact or “collapsed” forms of partially unfolded RNAs41 and stabilizes RNA tertiary structure much more effectively than secondary structure.57 However, the mechanisms by which a divalent cation and a neutral osmolyte affect RNA must be completely different, as diagramed in Figure 9. Mg2+ interacts favorably with both folded and unfolded forms of an RNA, primarily by strong attraction to the negative electrostatic field created by phosphates. However, interactions with the more compact native structure are stronger and lower its free energy relative to an unfolded state.33 In contrast, TMAO interacts unfavorably with both unfolded and folded RNA structures, but unfolded conformations expose more phosphate to solvent and have a more positive interaction free energy with TMAO. In a sense, Mg2+ "pulls" the folding equilibrium towards the native state by virtue of favorable interactions with the native RNA, while TMAO "pushes" the same equilibrium because of repulsive (unfavorable) interactions with partially unfolded RNA.
Figure 9.
Contrasting mechanisms by which Mg2+ and TMAO may stabilize the same RNA tertiary structure. The relative free energy (chemical potential) of folded (F) and unfolded (U) forms of a hypothetical RNA tertiary structure are diagrammed. In buffer, the U form of the RNA is represented as more stable than F (black boxes; the observed folding free energy, ΔG°obs, is positive). Mg2+ interacts strongly (red arrows) with both U and F forms of the RNA, but preferentially stabilizes the native structure (red boxes; ΔG°obs is now negative). TMAO interactions with both U and F forms are strongly unfavorable (blue arrows), but the U form is more strongly affected because of its more extensive exposure of phosphates to solvent. Therefore ΔG°obs becomes negative (blue boxes).
The case of the buried Mg2+ in the 58mer RNA is an example of how Mg2+ and TMAO can promote the same RNA structure by entirely different mechanisms. Four phosphates create two ion chelation sites in this RNA, one for K+ and one for Mg2+ (Figure 7A). The same selectivity for K+ and the same hydroxyl radical sensitivity is seen whether the Mg2+ site is occupied by ion or simply stabilized by TMAO (Figure 6C and 7B). In other work, we find that high concentrations of L11 protein (normally associated with this RNA domain in ribosomes) trap the RNA in its native conformation in the absence of Mg2+, with the sole exception of nucleotide A1073, which retains the reactivity of unfolded RNA to hydroxyl radical. K+ selectivity has been lost in this complex, presumably because of the non-native structure at A1073 (D. Leipply & D.E.D., ms. submitted).
We infer that there is a strong driving force for the A1073 phosphate to stay exposed to solvent, both because of electrostatic repulsion from nearby phosphates and from the energetic cost of phosphate dehydration, and suggest that the substantial free energy cost of burying this phosphate can be paid in two ways. One way is for Mg2+ to occupy the chelation site and reduce electrostatic repulsion among the phosphates; the favorable electrostatic energy of ion binding must be enough to overcome the dehydration penalty. The other way is for TMAO to reduce the dehydration penalty; the electrostatic repulsion between phosphates in the unoccupied site still remains, but is now insufficient to disrupt the native conformation. The surprising implication is that TMAO exclusion from this site generates stabilizing free energies as large as Mg2+ binding.
In summary, the parallel effects of Mg2+ and TMAO suggest that RNA phosphates present two different kinds of barriers to formation of tertiary structures: strong electrostatic repulsion between phosphates and strong interactions with water (hydration) both favor non-native, extended conformations of an RNA. Those barriers may be reduced because of net favorable interactions of ions with the native structure or because of unfavorable interactions with protecting osmolyte by the partially unfolded RNA (Figure 9). In either case, the same native structure is adopted, implying that the native tertiary structure is primarily specified by the RNA sequence. Ions and osmolyte facilitate RNA folding but do not organize the native structure, in the cases examined here.
MATERIALS AND METHODS
Chemicals and solutions
All solutions were prepared using distilled deionized water at 18.3MΩ resistivity. MOPS, potassium chloride, sodium chloride, and rubidium chloride (all >99.5% pure) were purchased from Fluka. Lithium chloride, cesium chloride, and EDTA (also >99.5% pure) were obtained from Sigma-Aldrich. Lithium hydroxide, sodium hydroxide, potassium hydroxide, rubidium hydroxide, cesium hydroxide (all 99.99% pure) and trimethyl phosphate (>99% pure) were purchased from Aldrich. Trimethylamine oxide dihydrate (TMAO) (≥99% pure) was purchased from Fluka; contaminating amines were removed by treating ~10 m TMAO (~175 g total) for several hours at room temperature with approximately 5 g of granular activated carbon (Darco, 20–40 mesh, Aldrich), followed by vacuum filtration using 0.22 µm Durapore membrane filters (Millipore). This procedure was repeated until no amine smell was detectable. The solution was then deionized using 2 g of mixed bed resin (AG 501-X8, 20–50 mesh, Bio Rad), divided into aliquots and stored at −80°C until used. By atomic absorbtion, the stock solution was less than 0.16 µM in Mg2+, which after dilution contributes less than 0.06 µm Mg2+ to a 2 m TMAO solution. This amount of Mg2+ is far less than the RNA concentrations typically used in melting experiments (~1 µm). The final concentrations of TMAO solutions were determined by stoichiometric titration with standardized HCl. We also confirmed that the vapor pressure of our potassium chloride solutions corresponded to literature values.25; 58
Potassium dimethylphosphate was synthesized by mixing equimolar amounts of trimethyl phosphate (Sigma-Aldrich) and KOH (Fluka) in 80% ethanol/water solution as described,59 with the exception that NaOH was substituted by KOH. Hydrolysis was allowed to proceed for at least four hours. The solution was then concentrated under vacuum, redissolved in water and subsequently passed through an ion exchange column (DOWEX 50WX8, Dow) to insure that that all the dimethyl phosphate was in the K+ salt form. The resulting solution was concentrated under vacuum until solid. No impurities were detected by phosphorus or proton NMR spectroscopy. Due to the hygroscopic nature of this salt, it was first stored in pre-weighed microtubes in a dessicator containing phosphorus pentoxide powder (98+%, A.C.S. Reagent, Sigma-Aldrich). Tubes were weighed under the dry atmosphere of a glove box every few days over the course of three weeks, until the weight stabilized. A 10 m stock was obtained by adding an appropriate weight of water to each tube, and the samples were stored at −80 °C.
The short hairpin oligonucleotides tar and tar* (Figure 1A, B) were purchased from Dharmacon and deprotected according the manufacturer's directions. Oligonucleotide length homogeneity was confirmed by denaturing polyacrylamide gel electrophoresis. The 58-mer rRNA fragment (Figure 1C), the tetraloop-receptor complex (Figure 1E), and the A-riboswitch aptamer domain (Figure 1D) were prepared by in vitro transcription with T7 RNA polymerase from linearized plasmid DNA and purified by denaturing polyacrylamide gel electrophoresis followed by electroelution, as described.12; 33 Before use, RNAs were extensively equilibrated with the appropriate buffers, using Amicon Ultra centrifugal filter devices (Millipore, Billerica, MA). Buffers for UV melting, VPO, and SAXS measurements are specified in the figure legends. MOPS buffer was adjusted to pH 7.0 or 6.8 with KOH (K-MOPS) or, for experiments done with other group I ions, the appropriate alkali metal hydroxide. The total K+ ion concentration is noted; it is the sum of K+ added from the K-MOPS buffer plus KCl.
All solutions with osmolyte were prepared in molal concentration units (moles solutes/Kg solvent) so that osmolyte and salt concentrations could be varied independently. Stock solution densities were used to calculate the volume of each needed to prepare samples for experiments. To determine densities, pipettors were first calibrated using the density of water at 20°C (0.997 g/mL). Then, precisely one mL of each solution was weighed on an analytical balance (Mettler Toledo).
UV thermal analysis
Melting experiments were performed in a Cary 400 spectrophotometer with 1 cm path length cuvettes. Absorbance data were collected at 260 and 280 (as well as 295 in the case of the 58mer rRNA fragment) nm from 5° to 95° C for the hairpin and the A-riboswitch, and from 2° to 95°C in the case the tar-tar* and the tetraloop-receptor complexes. Absorbance data for the small hairpin, which melts in a single transition, were analyzed by standard methods incorporating low and high temperature baselines as fitted variables.60 Data for the other RNAs studied were plotted as the first derivative of absorbance with respect to temperature (a melting profile). To simplify data analysis, sequential two-state transitions, defined by Tm, ΔH° (assumed to be independent from temperature), and amplitude of absorbance changes, were fit globally to both the 260 and 280 nm or 260 and 295nm data as described.61 Low temperature baselines for RNAs with tertiary structure are frequently small or zero, and only in a few cases were manually adjusted to optimize the fitted curve. Three transitions were fit to the tar-tar* and tetraloop-receptor data. Four transitions were used to fit the profile the 58mer rRNA as reported.29; 36 For this RNA, the enthalpies of the unfolding transitions obtained from experiments at 4 m TMAO were used to fit the data at 6 m TMAO, in accord with the observation that H° does not change with salt or osmolyte concentration.12 Characteristics of the A-riboswitch in melting experiments have recently been reported.31 The Tm of the first unfolding transition depends on the concentration of ligand (in this case, 2,6-diamino-purine, DAP) as expected for unfolding of tertiary structure; depending on the salt and osmolyte concentrations, we fit the melting profiles with either two or three transitions.
The averages and standard deviations of Tm and ΔH° for each RNA in the absence of osmolytes were previously determined;12; 29 ΔH° values agree within error with the values found in the presence of TMAO. Errors in Tm for individual melting curves were determined by a bootstrap method,61; 62 and were generally smaller than the plotted points (Figures 2 and S1). Global fitting of (1/Tm) as a function of both mTMAO and ln(mKCl) was performed with Pro Fit 6.1 using the following polynomial equation with six independent variables:
| (12) |
The six fitted coefficients were then multiplied by ΔH°/R to obtain derived parameters in terms of ln(Kobs). Errors reported in Table 2 were propagated using both the uncertainties in the fitted coefficients and in ΔH°; the latter were larger. The salt dependence at a specified TMAO concentration (cf. eq 3) is given by:
| (13) |
and in the absence of TMAO is just a0 (SKobs). The dependence of ln(Kobs) on osmolyte concentration at a specified KCl (cf. eq 5a) concentration is:
| (14) |
and the salt-TMAO interaction term in the limit of low TMAO concentration is a1.
A global fit of hairpin RNA 1/Tm values using eq 10 was unreliable because the salt – osmolyte interaction term (a1) was poorly determined. We therefore report parameters derived from the average slope of (1/Tm) vs. mTMAO or (1/Tm) vs. ln(mKCl) for this RNA in Table 2.
Isothermal titrations
Titrations of the A-riboswitch with TMAO were monitored by circular dichroism. The titrated solution had an initial concentration of 130 mm K-MOPS pH 7.0, 50 mm K+, 1 µm A-riboswitch RNA, and 10 µm adenine ligand. The titrant was the same, but with TMAO at a final concentration of 8.5 m. The RNA sample was first denatured for 10 minutes at 65°C, and brought to room temperature for approximately 10 minutes before titration was initiated. Titrations were performed at precisely 22.5°C with an Aviv Model 400 CD Spectrometer. A Hamilton Microlab 500 automated titrator was used to perform 37 injections. Data were collected at 268 nm with a bandwidth of 2 nm and averaging time of 30 sec. Titration data were fit to an equation with six variables specifying the slopes and intercepts of baselines for the unfolded and folded RNAs and a TMAO-dependent equilibrium constant expressed in terms of the midpoint of the titration and the m-value.
Vapor Pressure Osmometry
A Wescor VAPRO 5520 (Logan, UT) at ambient temperature (22.5°C) was used for all measurements. Three identical sample solutions in microtubes were assembled from water and stock solutions of known molality and density. Triplicate measurements of osmolality were made on each sample, for a total of nine readings. To minimize the concentration of protonated TMAO, 50 mm K-MOPS pH 7.0 was included in all samples. Controls done in the presence and absence of buffer showed a strictly additive effect of K-MOPS on the measured osmolalities. Data obtained in the presence and absence of TMAO were analyzed as described in Background (eq 7–9).
Hydroxyl radical footprinting
RNA for footprinting experiments was dephosphorylated for 5’ labeling by reaction with calf intestinal phosphatase at 37 °C for one hour, followed by phenol-chloroform extraction and ethanol precipitation to remove the enzyme and recover the RNA. 80 pmol of RNA was then end-labeled in 20 µL reactions with 10 µL γ32P-ATP (6000 Ci/mmol, from Perkin Elmer) and 10 units of polynucleotide kinase in the appropriate kinase buffer (NEB). Samples were gel-purified post-labeling on 12 or 16% denaturing acrylamide gels, and RNA recovered by freeze-thaw and ethanol precipitation. Each footprinting reaction contained 106 cpm of RNA in K-MOPS buffer and the desired amount of TMAO or Mg2+. On ice, H2O2 was added to 0.03%, and the Fe-EDTA complex to 1 mM ferrous ammonium sulfate and 2 mM EDTA, after degassing the solution. Reactions were quenched after 1 minute with thiourea. RNA was recovered by ethanol precipitation and resuspended in10 µL formamide loading buffer. 5 µL of each sample, along with unreacted, alkaline hydrolysis, and T1 digest controls, were loaded on a denaturing sequencing gels (12% for A-riboswitch RNA, 16% for 58mer RNA) and run for 3 hours at 70 watts. The gel was then transferred to Whatman filter paper, dried, and exposed to a phosphorimager screen for 18 hours before being imaged. The cleavage products in the sequencing gels were quantified using SAFA.63 Five invariant residues (C1064, A1067, C1075, U1083, G1091, and G1099) were chosen to normalize the band intensities in the 58mer. Four invariant residues (U36, G43, U62, G78) were chosen to normalize the band intensities in the adenine riboswitch.
Small Angle X-ray scattering
Small-angle X-ray scattering (SAXS) experiments were performed at beamlines 12-ID and 18-ID of the Advanced Photon Source (APS) at Argonne National Laboratory. The wavelength of incident X-ray radiation was set to 1.033 Å (a beam energy of 12 keV), the exposure time was 0.15 seconds, and samples were flowed through an X-ray flow cell while in the path of the beam to avoid radiation damage. RNA samples for the measurements were extensively exchanged into the appropriate KMOPS buffer supplemented with the salt and osmolyte concentrations of interest. The ambient temperature of the experiment was ~29 °C; samples were allowed to temperature equilibrate for an hour prior to beam exposure.
Twenty images were collected for each sample or buffer solution in order to obtain good statistics. Aberrant data sets were removed, and the remaining two-dimensional images from the CCD were reduced to one-dimensional scattering profiles using the program MarDetector (from Dr. David Tiede, unpublished). The resulting data sets were averaged prior to background subtraction of the buffer. The scattering profile of the RNA was then calculated using the following equation:
| (15) |
where I(q) is the appropriate scattering intensity at momentum transfer vector q = 4π sin(θ/γ) (where 2θ is the scattering angle) and α is scaling factor that takes into account the partial molar volume of RNA. The radius of gyration (Rg) was obtained from linear fits of the data with q*Rg < 1.2), using the Guinier approximation:
| (16) |
The program GNOM was used to compute distance distribution functions, P(r), from the scattering profiles.64 The Dmax parameter was systematically varied until consistent solutions were attained. The Rg values calculated from integration of P(r) agreed well (within 10%) with those obtained from Guinier analysis, validating the choice of Dmax. CRYSOL65 was used to calculate the expected Rg of native A-riboswitch (1Y26) and 58mer RNA (1HC8) from the indicated PDB files.
SASA calculations
Surface area calculations were performed using the program Surface Racer66 with the Richards parameters67 and probe radii of 1.4Å or 2.8Å.
Supplementary Material
Acknowledgements
This work was supported by NIH grants RO1 GM58545 and T32 GM008403 (Program in Molecular Biophysics). We thank Sean Campbell and Kenny Xu for assistance with VPO measurements, and Drs. Xiaobing Zuo and Sonke Seifert for help with collection and analysis of the scattering data.
Abbreviations used
- TMAO
trimethylamine oxide
- DAP
2,6-diamino-purine
- CD
circular dichroism
- SAXS
small angle X-ray scattering
- VPO
vapor pressure osmometry
- TLR
tetraloop receptor RNA
- K-DMP
potassium dimethylphosphate
- SASA
solvent-accessible surface area
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Supplementary Data
Supplementary data can be found online at doi _________. The file includes plots of the dependences of ln(Kobs) on salt or TMAO concentrations for the hairpin, tar-tar* complex, and TLR RNA (Figure S1), isothermal titrations monitored by CD for the A-riboswitch (Figure S2), osmolality vs. m2m3 plots for uridine, cytidine, and purine with TMAO (Figure S3); and the distance distribution function of the A-riboswitch at various TMAO concentrations (Figure S4).
It is not possible to measure μ23 for individual ions, only the sum of the anion and cation contributions. In calculating the proportionality factor for backbone phosphate, we are assuming that the measured μ23/RT ≈ 0 for KCl results from a 0 value for both K+ and Cl−. In an extensive study of glycine betaine with various compounds and salts, Capp et al.24 derived a self-consistent set of μ23 values in which μ23/RT was assigned to 0 for Na+; μ23/RT then took on the values −0.03 for Cl− and +0.09 for K+. As TMAO is chemically similar to glycine betaine and has a net weaker interaction with KCl, it seems reasonable to assume that interactions with either K+ or Cl− will be small compared to the magnitude of the interaction with DMP−. We have also neglected the exclusion of TMAO by the two methyl groups of DMP−; aliphatic carbons interact with glycine betaine an order of magnitude more weakly than anionic oxygen.24
References
- 1.Yancey PH, Clark ME, Hand SC, Bowlus RD, Somero GN. Living with water stress: evolution of osmolyte systems. Science. 1982;217:1214–1222. doi: 10.1126/science.7112124. [DOI] [PubMed] [Google Scholar]
- 2.Cayley DS, Guttman HJ, Record MT., Jr Biophysical characterization of changes in amounts and activity of Escherichia coli cell and compartment water and turgor pressure in response to osmotic stress. Biophys J. 2000;78:1748–1764. doi: 10.1016/s0006-3495(00)76726-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Liu Y, Bolen DW. The peptide backbone plays a dominant role in protein stabilization by naturally occurring osmolytes. Biochemistry. 1995;34:12884–12891. doi: 10.1021/bi00039a051. [DOI] [PubMed] [Google Scholar]
- 4.Timasheff SN. Control of protein stability and reactions by weakly interacting cosolvents: the simplicity of the complicated. Adv Protein Chem. 1998;51:355–432. doi: 10.1016/s0065-3233(08)60656-7. [DOI] [PubMed] [Google Scholar]
- 5.Courtenay ES, Capp MW, Saecker RM, Record MT., Jr Thermodynamic analysis of interactions between denaturants and protein surface exposed on unfolding: interpretation of urea and guanidinium chloride m-values and their correlation with changes in accessible surface area (ASA) using preferential interaction coefficients and the local-bulk domain model. Proteins Suppl. 2000;4:72–85. doi: 10.1002/1097-0134(2000)41:4+<72::aid-prot70>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 6.Bolen DW, Baskakov IV. The osmophobic effect: natural selection of a thermodynamic force in protein folding. J Mol Biol. 2001;310:955–963. doi: 10.1006/jmbi.2001.4819. [DOI] [PubMed] [Google Scholar]
- 7.Felitsky DJ, Cannon JG, Capp MW, Hong J, Van Wynsberghe AW, Anderson CF, Record MT., Jr The exclusion of glycine betaine from anionic biopolymer surface: why glycine betaine is an effective osmoprotectant but also a compatible solute. Biochemistry. 2004;43:14732–14743. doi: 10.1021/bi049115w. [DOI] [PubMed] [Google Scholar]
- 8.Auton M, Bolen DW. Predicting the energetics of osmolyte-induced protein folding/unfolding. Proc Natl Acad Sci U S A. 2005;102:15065–15068. doi: 10.1073/pnas.0507053102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bolen DW, Rose GD. Structure and energetics of the hydrogen-bonded backbone in protein folding. Annu Rev Biochem. 2008;77:339–362. doi: 10.1146/annurev.biochem.77.061306.131357. [DOI] [PubMed] [Google Scholar]
- 10.Baskakov I, Bolen DW. Forcing thermodynamically unfolded proteins to fold. J Biol Chem. 1998;273:4831–4834. doi: 10.1074/jbc.273.9.4831. [DOI] [PubMed] [Google Scholar]
- 11.Baskakov IV, Kumar R, Srinivasan G, Ji YS, Bolen DW, Thompson EB. Trimethylamine N-oxide-induced cooperative folding of an intrinsically unfolded transcription-activating fragment of human glucocorticoid receptor. J Biol Chem. 1999;274:10693–10696. doi: 10.1074/jbc.274.16.10693. [DOI] [PubMed] [Google Scholar]
- 12.Lambert D, Draper DE. Effects of Osmolytes on RNA Secondary and Tertiary Structure Stabilities and RNA-Mg2+ Interactions. J Mol Biol. 2007;370:993–1005. doi: 10.1016/j.jmb.2007.03.080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pan T, Sosnick TR. Intermediates and kinetic traps in the folding of a large ribozyme revealed by circular dichroism and UV absorbance spectroscopies and catalytic activity. Nat Struct Biol. 1997;4:931–938. doi: 10.1038/nsb1197-931. [DOI] [PubMed] [Google Scholar]
- 14.Wyman J. Heme Proteins. Adv Protein Chem. 1948;4:407–531. doi: 10.1016/s0065-3233(08)60011-x. [DOI] [PubMed] [Google Scholar]
- 15.Record MT, Jr, Zhang W, Anderson CF. Analysis of effects of salts and uncharged solutes on protein and nucleic acid equilibria and processes: a practical guide to recognizing and interpreting polyelectrolyte effects, Hofmeister effects, and osmotic effects of salts. Adv Protein Chem. 1998;51:281–353. doi: 10.1016/s0065-3233(08)60655-5. [DOI] [PubMed] [Google Scholar]
- 16.Leipply D, Lambert D, Draper DE. Ion–RNA Interactions: Thermodynamic Analysis of the Effects of Mono- and Divalent Ions on RNA Conformational Equilibria. Methods in Enzymology. 2009;469:433–463. doi: 10.1016/S0076-6879(09)69021-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hong J, Capp MW, Saecker RM, Record MT., Jr Use of urea and glycine betaine to quantify coupled folding and probe the burial of DNA phosphates in lac repressor-lac operator binding. Biochemistry. 2005;44:16896–16911. doi: 10.1021/bi0515218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hong J. Solute probes of changes in water accessible biopolymer surface: Development and application to Lac Repressor. Madison: University of Wisconsin; 2004. [Google Scholar]
- 19.Pace CN. The stability of globular proteins. CRC Crit Rev Biochem. 1975;3:1–43. doi: 10.3109/10409237509102551. [DOI] [PubMed] [Google Scholar]
- 20.Robinson RA, Sinclair DA. The Activity Coefficients of the Alkali Chlorides and of Lithium Iodide in Aqueous Solution from Vapor Pressure Measurements. J Am Chem Soc. 1934;59:1830–1835. [Google Scholar]
- 21.Pitzer KS. Thermodynamics. 3rd edit. Nw York: McGraw-Hill, Inc.; 1995. [Google Scholar]
- 22.Robinson CV, Stokes RH. Activity coefficients in aqueous solutions of sucrose, mannitol and their mixtures at 25°. J Phys Chem. 1961;65:1954–1958. [Google Scholar]
- 23.Cannon JG, Anderson CF, Record MT., Jr Urea-amide preferential interactions in water: quantitative comparison of model compound data with biopolymer results using water accessible surface areas. J Phys Chem B. 2007;111:9675–9685. doi: 10.1021/jp072037c. [DOI] [PubMed] [Google Scholar]
- 24.Capp MW, Pegram LM, Saecker RM, Kratz M, Riccardi D, Wendorff T, Cannon JG, Record MT., Jr Interactions of the osmolyte glycine betaine with molecular surfaces in water: thermodynamics, structural interpretation, and prediction of m-values. Biochemistry. 2009;48:10372–10379. doi: 10.1021/bi901273r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hong J, Capp MW, Anderson CF, Record MT. Preferential interactions in aqueous solutions of urea and KCl. Biophys Chem. 2003;105:517–532. doi: 10.1016/s0301-4622(03)00112-1. [DOI] [PubMed] [Google Scholar]
- 26.Chang K-Y, Tinoco I. The Structure of an RNA "Kissing" Hairpin Complex of the HIV TAR Hairpin Loop and its Complement. J Mol Biol. 1997;269:52–66. doi: 10.1006/jmbi.1997.1021. [DOI] [PubMed] [Google Scholar]
- 27.Davis JH, Tonelli M, Scott LG, Jaeger L, Williamson JR, Butcher SE. RNA helical packing in solution: NMR structure of a 30 kDa GAAA tetraloop-receptor complex. J Mol Biol. 2005;351:371–382. doi: 10.1016/j.jmb.2005.05.069. [DOI] [PubMed] [Google Scholar]
- 28.Zuo X, Wang J, Foster TR, Schwieters CD, Tiede DM, Butcher SE, Wang YX. Global molecular structure and interfaces: refining an RNA:RNA complex structure using solution X-ray scattering data. J Am Chem Soc. 2008;130:3292–3293. doi: 10.1021/ja7114508. [DOI] [PubMed] [Google Scholar]
- 29.Lambert D, Leipply D, Shiman R, Draper DE. The influence of monovalent cation size on the stability of RNA tertiary structures. J Mol Biol. 2009;390:791–804. doi: 10.1016/j.jmb.2009.04.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Serganov A, Yuan YR, Pikovskaya O, Polonskaia A, Malinina L, Phan AT, Hobartner C, Micura R, Breaker RR, Patel DJ. Structural basis for discriminative regulation of gene expression by adenine- and guanine-sensing mRNAs. Chem Biol. 2004;11:1729–1741. doi: 10.1016/j.chembiol.2004.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Leipply D, Draper DE. The dependence of RNA tertiary structure stability on Mg2+ concentration: interpretation of the Hill equation and coefficient. Biochemistry. 2010;49:1843–1853. doi: 10.1021/bi902036j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Conn GL, Gittis AG, Lattman EE, Misra VK, Draper DE. A compact RNA tertiary structure contains a buried backbone-K+ complex. J Mol Biol. 2002;318:963–973. doi: 10.1016/S0022-2836(02)00147-X. [DOI] [PubMed] [Google Scholar]
- 33.Grilley D, Soto AM, Draper DE. Mg2+-RNA interaction free energies and their relationship to the folding of RNA tertiary structures. Proc Natl Acad Sci U S A. 2006;103:14003–14008. doi: 10.1073/pnas.0606409103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Misra VK, Draper DE. A thermodynamic framework for Mg2+ binding to RNA. Proc Natl Acad Sci U S A. 2001;98:12456–12461. doi: 10.1073/pnas.221234598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bukhman YV, Draper DE. Affinities and Selectivities of Divalent Cation Binding Sites Within an RNA Tertiary Structure. J Mol Biol. 1997;273:1020–1031. doi: 10.1006/jmbi.1997.1383. [DOI] [PubMed] [Google Scholar]
- 36.Shiman R, Draper DE. Stabilization of RNA tertiary structure by monovalent cations. J Mol Biol. 2000;302:79–91. doi: 10.1006/jmbi.2000.4031. [DOI] [PubMed] [Google Scholar]
- 37.Lu M, Draper DE. Bases defining an ammonium and magnesium ion-dependent tertiary structure within the large subunit ribosomal RNA. J Mol Biol. 1994;244:572–585. doi: 10.1006/jmbi.1994.1753. [DOI] [PubMed] [Google Scholar]
- 38.Ts'o POP, Melvin IS, Olson AC. Interaction and Association of Bases and Nucleosides in Aqueous Solutions. J Am Chem Soc. 1963;85:1289–1296. doi: 10.1021/ja00950a045. [DOI] [PubMed] [Google Scholar]
- 39.Qu Y, Bolen CL, Bolen DW. Osmolyte-driven contraction of a random coil protein. Proc Natl Acad Sci U S A. 1998;95:9268–9273. doi: 10.1073/pnas.95.16.9268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Allen SH, Wong KP. The role of magnesium and potassium ions in the molecular mechanism of ribosome assembly: hydrodynamic, conformational, and thermal stability studies of 16 S RNA from Escherichia coli ribosomes. Arch Biochem Biophys. 1986;249:137–147. doi: 10.1016/0003-9861(86)90568-0. [DOI] [PubMed] [Google Scholar]
- 41.Buchmueller KL, Webb AE, Richardson DA, Weeks KM. A collapsed non-native RNA folding state. Nat Struct Biol. 2000;7:362–366. doi: 10.1038/75125. [DOI] [PubMed] [Google Scholar]
- 42.Perez-Salas UA, Rangan P, Krueger S, Briber RM, Thirumalai D, Woodson SA. Compaction of a bacterial group I ribozyme coincides with the assembly of core helices. Biochemistry. 2004;43:1746–1753. doi: 10.1021/bi035642o. [DOI] [PubMed] [Google Scholar]
- 43.Takamoto K, Das R, He Q, Doniach S, Brenowitz M, Herschlag D, Chance MR. Principles of RNA compaction: insights from the equilibrium folding pathway of the P4-P6 RNA domain in monovalent cations. J Mol Biol. 2004;343:1195–1206. doi: 10.1016/j.jmb.2004.08.080. [DOI] [PubMed] [Google Scholar]
- 44.Grilley D, Misra V, Caliskan G, Draper DE. Importance of Partially Unfolded Conformations for Mg(2+)-Induced Folding of RNA Tertiary Structure: Structural Models and Free Energies of Mg(2+) Interactions. Biochemistry. 2007;46:10266–10278. doi: 10.1021/bi062284r. [DOI] [PubMed] [Google Scholar]
- 45.Lemay JF, Penedo JC, Tremblay R, Lilley DM, Lafontaine DA. Folding of the adenine riboswitch. Chem Biol. 2006;13:857–868. doi: 10.1016/j.chembiol.2006.06.010. [DOI] [PubMed] [Google Scholar]
- 46.Celander DW, Cech TR. Visualizing the higher order folding of a catalytic RNA molecule. Science. 1991;251:401–407. doi: 10.1126/science.1989074. [DOI] [PubMed] [Google Scholar]
- 47.Balasubramanian B, Pogozelski WK, Tullius TD. DNA strand breaking by the hydroxyl radical is governed by the accessible surface areas of the hydrogen atoms of the DNA backbone. Proc Natl Acad Sci U S A. 1998;95:9738–9743. doi: 10.1073/pnas.95.17.9738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Noto R, Martorana V, Emanuele A, Fornill SL. Comparison of the Water Perturbations induced by Two Small Organic Solutes : Ab initio Calculations and Molecular Dynamics Simulation. J Chem Soc Faraday Trans. 1995;91:3803–3808. [Google Scholar]
- 49.Schwinefus JJ, Kuprian MJ, Lamppa JW, Merker WE, Dorn KN, Muth GW. Human telomerase RNA pseudoknot and hairpin thermal stability with glycine betaine and urea: preferential interactions with RNA secondary and tertiary structures. Biochemistry. 2007;46:9068–9079. doi: 10.1021/bi602637v. [DOI] [PubMed] [Google Scholar]
- 50.Hong J, Capp MW, Anderson CF, Saecker RM, Felitsky DJ, Anderson MW, Record MT., Jr Preferential interactions of glycine betaine and of urea with DNA: implications for DNA hydration and for effects of these solutes on DNA stability. Biochemistry. 2004;43:14744–14758. doi: 10.1021/bi049096q. [DOI] [PubMed] [Google Scholar]
- 51.Costa M, Deme E, Jacquier A, Michel F. Multiple tertiary interactions involving domain II of group II self-splicing introns. J Mol Biol. 1997;267:520–536. doi: 10.1006/jmbi.1996.0882. [DOI] [PubMed] [Google Scholar]
- 52.Cate JH, Gooding AR, Podell E, Zhou K, Golden BL, Kundrot CE, Cech TR, Doudna JA. Crystal structure of a group I ribozyme domain: principles of RNA packing. Science. 1996;273:1678–1685. doi: 10.1126/science.273.5282.1678. [DOI] [PubMed] [Google Scholar]
- 53.Adams PL, Stahley MR, Kosek AB, Wang J, Strobel SA. Crystal structure of a self-splicing group I intron with both exons. Nature. 2004;430:45–50. doi: 10.1038/nature02642. [DOI] [PubMed] [Google Scholar]
- 54.Lebars I, Legrand P, Aime A, Pinaud N, Fribourg S, Di Primo C. Exploring TAR-RNA aptamer loop-loop interaction by X-ray crystallography, UV spectroscopy and surface plasmon resonance. Nucleic Acids Res. 2008;36:7146–7156. doi: 10.1093/nar/gkn831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Creamer TP, Srinivasan R, Rose GD. Modeling unfolded states of peptides and proteins. Biochemistry. 1995;34:16245–16250. doi: 10.1021/bi00050a003. [DOI] [PubMed] [Google Scholar]
- 56.Shortle D, Ackerman MS. Persistence of native-like topology in a denatured protein in 8 M urea. Science. 2001;293:487–489. doi: 10.1126/science.1060438. [DOI] [PubMed] [Google Scholar]
- 57.Stein A, Crothers DM. Conformational Changes of Transfer RNA. The Role of Magnesium(II) Biochemistry. 1976;15:160–167. doi: 10.1021/bi00646a025. [DOI] [PubMed] [Google Scholar]
- 58.Robinson CV, Stokes RH. Electrolyte Solutions. Second Revised Edition. Minoeola, NY: Dover Publications; 2002. [Google Scholar]
- 59.McIvor RA, McCarthy GD, Grant GA. Preparation and toxicity of some alkyl thiophosphates. Can J Chem. 1956;34:1819–1832. [Google Scholar]
- 60.Petersheim M, Turner DH. Base-stacking and Base-Pairing Contributions to Helix Stability: Thermodynamics of Double-Helix Formation with CCGG, CCGGp,CCGGAp, CCGGUp, and ACCGGUp. Biochemistry. 1983;22:256–263. doi: 10.1021/bi00271a004. [DOI] [PubMed] [Google Scholar]
- 61.Draper DE, Bukhman YV, Gluick TC. Thermal Methods for the Analysis of RNA Folding Pathways. In: Beaucage SL, Bergstrom DE, Glick GD, Jones RA, editors. Current Protocols in Nucleic Acid Chemistry. New York: John Wiley & Sons; 2000. section 11.3. [DOI] [PubMed] [Google Scholar]
- 62.Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C. Cambridge: Cambridge University Press; 1992. [Google Scholar]
- 63.Das R, Laederach A, Pearlman SM, Herschlag D, Altman RB. SAFA: semi-automated footprinting analysis software for high-throughput quantification of nucleic acid footprinting experiments. Rna. 2005;11:344–354. doi: 10.1261/rna.7214405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Svergun DI, Koch MJH. Small-angle scattering studies of biological macromolecules in solution. Reports Prog Phys. 2003;66:1735–1782. [Google Scholar]
- 65.Svergun DI, Barberato C, Koch MJH. CRYSOL- A program to evaluate x-ray solution scattering of biological macromolecules from atomic coordinates. Journal of Applied Crystallography. 1995;25:495–503. [Google Scholar]
- 66.Tsodikov OV, Record MT, Jr, Sergeev YV. Novel computer program for fast exact calculation of accessible and molecular surface areas and average surface curvature. J Comput Chem. 2002;23:600–609. doi: 10.1002/jcc.10061. [DOI] [PubMed] [Google Scholar]
- 67.Richmond TJ, Richards FM. Packing of alpha-helices: geometrical constraints and contact areas. J Mol Biol. 1978;119:537–555. doi: 10.1016/0022-2836(78)90201-2. [DOI] [PubMed] [Google Scholar]
- 68.Courtenay ES, Capp MW, Anderson CF, Record MT., Jr Vapor pressure osmometry studies of osmolyte-protein interactions: implications for the action of osmoprotectants in vivo and for the interpretation of "osmotic stress" experiments in vitro. Biochemistry. 2000;39:4455–4471. doi: 10.1021/bi992887l. [DOI] [PubMed] [Google Scholar]
- 69.Pauling L. The Nature of the Chemical Bond. Ithaca, NY: Cornell University Press; 1960. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.