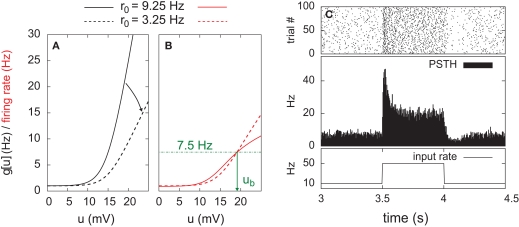
Figure 1.

Stochastic neuron model. (A) The gain function g(u) (Eq. 4, solid line here) shows the momentary rate of a non-refractory neuron as a function of the membrane potential u. (B) The mean rate 〈g[u(t)]M(t)〉 of a neuron with refractoriness and adaptation is lower (solid red line). The baseline potential u_b used in the simulation is defined as the membrane potential that yields a spontaneous firing rate of 7.5 Hz (green arrow and dashed line). In some simulations, we need to switch off adaptation, but we want the same holding potential u_b to evoke the same 7.5 Hz output firing rate. The slope r₀ of the gain function is therefore rescaled (A, dashed curve) so that the frequency curves in the adaptation and no-adaptation cases (B, solid and dashed red curves) cross at u = u_b. (C) Example response property of an adaptive neuron. A single neuron receives synaptic inputs from 100 Poisson spike trains with a time-varying rate. The experiment is repeated 1000 times independently. Bottom: the input rate jumps from 10 to 50 Hz, stays there for half a second and returns back to 10 Hz (bottom). Middle: Peri-stimulus time histogram (PSTH, 4 ms bin). Top: example spike trains (first 100 trials).