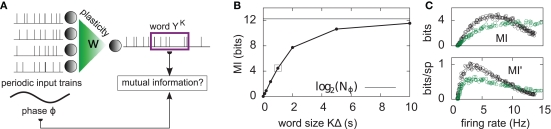
Figure 2.

Information transmission through a noisy postsynaptic neuron. (A) Schematic representation of the feed-forward network. Five-second input spike trains repeat continuously in time (periodic input) and drive a noisy and possibly adapting output neuron via plastic synapses. It is assumed that an observer of the output spike train has access to portions Y^K of it, called “words,” of duration T = KΔ. The observer does not have access to a clock, and therefore has a flat prior expectation over possible phases before observing a word. The goodness of the system, given a set of synaptic weights w, is measured by the reduction of uncertainty about the phase, gained from the observation of an output word Y^K (mutual information, see text). (B) For a random set of synaptic weights (20 weights at 4 mV, the rest at 0), the mutual information (MI) is reported as a function of the output word size KΔ. Asymptotically, the MI converges to the theoretical limit given by log₂(N_φ) ( 12.3 bits. In the rest of this study, 1-s output words are considered (square). (C) Mutual information (MI, top) and information per spike (MI’, bottom) as a function of the average firing rate. Black: with SFA. Green: without SFA. Each dot is obtained by setting a fraction of randomly chosen synaptic efficacies to the upper bound (4 mV) and the rest to 0. The higher the fraction of non-zero weights, the higher the firing rate. The information per spike is a relevant quantity because spike generation costs energy.