Multi-Organ Segmentation from Multi-Phase Abdominal CT via 4D Graphs using Enhancement, Shape and Location Optimization

Abstract

The interpretation of medical images benefits from anatomical and physiological priors to optimize computer-aided diagnosis (CAD) applications. Diagnosis also relies on the comprehensive analysis of multiple organs and quantitative measures of soft tissue. An automated method optimized for medical image data is presented for the simultaneous segmentation of four abdominal organs from 4D CT data using graph cuts. Contrast-enhanced CT scans were obtained at two phases: non-contrast and portal venous. Intra-patient data were spatially normalized by non-linear registration. Then 4D erosion using population historic information of contrast-enhanced liver, spleen, and kidneys was applied to multi-phase data to initialize the 4D graph and adapt to patient specific data. CT enhancement information and constraints on shape, from Parzen windows, and location, from a probabilistic atlas, were input into a new formulation of a 4D graph. Comparative results demonstrate the effects of appearance and enhancement, and shape and location on organ segmentation.

1 Introduction

In current CT-based clinical abdominal diagnosis, radiologists rely on analyzing multiphase CT data, as soft tissue enhancement can be an indicator of abnormality. This makes multi-phase data (with/without contrast) readily available. Diagnosis also relies on the comprehensive analysis of groups of organs and quantitative measures of soft tissue, as the volumes and shapes of organs can be indicators of disorders.

Computer-aided diagnosis (CAD) and medical image analysis traditionally focus on organ- or disease-based applications. However there is a strong incentive to migrate toward the automated simultaneous segmentation and analysis of multiple organs for comprehensive diagnosis or pre-operative planning and guidance. Additionally, the interpretation of medical images should benefit from anatomical and physiological priors, such as shape and appearance; synergistic combinations of priors were seldom incorporated in the optimization of CAD.

The segmentation of abdominal organs was initialized from probabilistic atlases in [10] using relationships between organs and manual landmarks. Alternatively, multidimensional contrast-enhanced CT data were employed in [5,7,13]. In [5,13] the segmentation used independent component analysis in a Bayesian framework. A 4D convolution was proposed in [7] constrained by a historic model of abdominal soft tissue enhancement. These intensity-based methods are hampered by the high variability of abdominal intensity and texture. More recently, a hierarchical multi-organ statistical atlas was developed [9]; the analysis was restricted to the liver area due to large variations to be statistically modeled for inter-organ relationships.

On a different note, graph cuts [2] have become popular for image segmentation, due to their ability to handle highly textured data via a numerically robust global optimization. A major drawback remains the manual initialization of such applications [4,8,16]. In [1,6] model-based information was included for the heart and kidney; however the models were aligned using markers. Compact shape priors were used in [4], but medical data often involves complex shapes. A shape model was also integrated in [15] as a density estimation for shape priors, initially proposed for level sets in [3], but a symmetric shape distance can be biased if shape initialization is poor.

We propose a new formulation of a 4D directional graph to automatically segment abdominal organs, at this stage the liver, spleen, and left and right kidneys using graph cuts. The approach is optimized to medical images through the use of location probabilistic priors that are intrinsic to medical data, an enhancement constraint characteristic to the clinical protocols using abdominal CT, and an asymmetric shape distance that avoids shape bias to build Parzen windows. The method is optimized globally and starts with historic (entire patient population) 4D intensity data to automatically initialize the graph, then migrating to patient specific information for better specificity. Comparative results at different stages of the algorithm show the effects of appearance, shape and location on the accuracy of organ segmentation.

2 Methods and Materials

Data, Preprocessing and Model Initialization

Eight random abdominal CT studies (normal and abnormal) were obtained with two temporal acquisitions. The first image was obtained at non-contrast phase (NCP) and a second at portal venous phase (PVP) using fixed delays. The CT data were collected on LightSpeed Ultra and QX/I scanners [GE Healthcare] at multiple time points. Image resolution ranged from 0.62 to 0.82 mm in the axial view with a slice thickness of 5 mm. The algorithm was trained and tested with a leave-one-out strategy.

The liver, spleen, and left and right kidneys were manually segmented (by two research fellows supervised by a board-certified radiologist) in the 8 CT cases using the PVP CT volumes to provide a gold standard for testing the method. Histograms of the segmented organs (objects) and background in NCP and PVP were computed and modeled as sums of Gaussians, as in Figure 1. While there are partial overlaps between the object and background distributions (especially at NCP), the combination of multi-phase data ensures a better separation.

Figure 1.

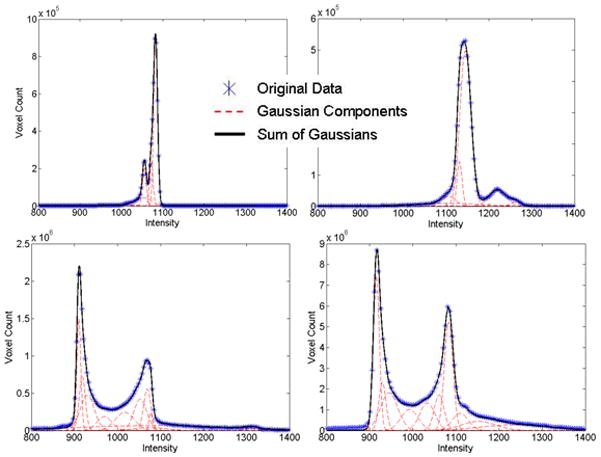
Fitted sums of Gaussians to historic data of organs/objects (top row) and background (bottom row). NCP data is shown on the left column and PVP data on the right. Historic data we refer to the training cases in the leave-one-out strategy.

Although images were acquired during the same session and intra-patient, there was small, but noticeable abdominal inter-phase motion, especially associated with breathing. The preprocessing follows the work in [7]. Data were smoothed using anisotropic diffusion [12]. NCP data were registered to the PVP images. The demons non-linear registration algorithm was employed [14], as the limited range of motion ensures partial overlaps between organs over multiple phases. The deformation field F of image I to match image J is governed by the optical flow equation

$$F=\frac{(I-J)\nabla J}{{\left|\right|\nabla J\left|\right|}^2+{(I-J)}^2};$$ (1)

A probabilistic atlas (PA) was constructed from a different set of 10 non contrast CT from healthy cases, independent from the data above, with manually segmented liver, spleen and kidneys. Organ locations were normalized to an anatomical landmark (xiphoid) to preserve spatial relationships and model organs in the anatomical space. The tip of the xiphoid (an ossified cartilaginous extension below the sternal notch) was extracted manually in the data used in the location model. A random image set was used as reference and the remaining images registered to it. Structural variability including the size of organs was conserved by a size-preserving affine registration. The location bias was minimized by the normalization by the xiphoid. The 10 unprocessed CT data were further used to build shape constraints via a Parzen window distribution, as explained in the construction of the 4D graph.

4D Convolution

From smoothed historic data of contrast-enhanced CT, the min and max intensities for the organs were estimated: min_i,t = μ_i,t − 3σ_i,t and max_i.t = μ_i,t + 3σ_i,t, where i=1..3 for liver, spleen and kidneys, μ_p,t and σ_p,t represent the mean and standard deviation, and t=1,2 for NCP and PVP. As in [7], a 4D array K(x,y,z,t)=I_t(x,y,z) was created from multi-phase data. A convolution with a 4D filter f labeled only regions for which all voxels in the convolution kernel satisfied the intensity constraints. L represents the labeled image and l_j the labels (j=1..4 for liver, spleen, left kidney and right kidney).

$$L(x,y,z)=(K\circ f)(x,y,z,t)=\{\begin{array}{l}{l}_j,if\underset{t}{\cap }\left({min}_{jt}\le K(x,y,z,t)\le {max}_{jt}\right)\hfill \\ 0,\mathit{otherwise}\hfill \end{array};$$ (2)

The labeled organs in L appear eroded as a result of the 4D convolution. In our method, L provided seeds for objects (I_o) in the 4D graph and was used to estimate the patient-specific histograms. The eroded inverted L provided the background (I_b) seeds and the related histograms. To report the segmentation results by 4D convolution (see Results), L was dilated to compensate for the undersegmentation of organs.

4D Graph

Graph cuts (GC) were chosen for the inherent capability to provide a globally optimal solution [2]. The input to our problem is two sets of registered abdominal CT scans per patient: the NCP and PVP sequences. Hence every voxel p in the graph has two intensity values $I_{\mathit{ncp}}^p$ and $I_{\mathit{pcp}}^p$. Let A = (A₁, A₂, …, A_p, …, A_P) be a binary vector with components A_p that can be either objects of interest (i.e. liver, spleen and kidneys) denoted by O or background B, where B∩O= Ø. Typical graphs perform data labeling (t-links), via log-likelihoods based solely on 2D or 3D interactive histogram fitting, and penalize neighborhood changes (n-links) through likelihoods from the image contrast [2]. We first extend the formulation to analyze 4D data, and then incorporate penalties from the contrast enhancement of CT soft tissue, Parzen shape windows, and location from a priori probabilities. While location knowledge was incorporated in the labeling of objects, shape information penalized boundaries not resembling the references. The cost function E to minimize becomes

$$E(A)=E_{\mathit{data}}(A)+E_{\mathit{enhance}}(A)+E_{\mathit{location}}(A)+{\sum }_{i=1}^4\left(E_{\mathit{boundary}}(A)+E_{\mathit{shape}}(A)\right);$$ (3)

The first three terms define the objects (t-links) and the last two energies find the cuts (n-links) with i=1..4 for liver, spleen, left kidney and right kidney. In this application, E_data is a regional term that computes penalties based on 4D histograms of O and B; the probabilities P of a voxel to belong to O or B are computed from patient specific histograms of NCP and PVP data.

$$\begin{array}{l}{E}_{\mathit{data}}(A)=\lambda \sum _{p\in O}{R}_p(O)+(1-\lambda )\sum _{p\in B}{R}_p(B);\\ R_p(O)=-ln\left(\sqrt{P_{\mathit{ncp}}(I_{\mathit{ncp}}^p\mid O)P_{\mathit{pvp}}(I_{\mathit{pvp}}^p\mid O)}/\left(\sqrt{P_{\mathit{ncp}}(I_{\mathit{ncp}}^p\mid O)P_{\mathit{pvp}}(I_{\mathit{pvp}}^p\mid O)}+\sqrt{P_{\mathit{ncp}}(I_{\mathit{ncp}}^p\mid B)P_{\mathit{pvp}}(I_{\mathit{pvp}}^p\mid B)}\right)\right);\end{array}$$ (4)

E_enhance penalizes regions that do not enhance rapidly during the acquisition of NCP-PVP CT data (i.e. muscles, ligaments and marrow). σ_ncp and σ_pvp are the standard deviations of noise associated with NCP and PVP.

$$E_{\mathit{enhance}}(A)=\sum _{p\in P}1/\left(1+E_p^2\right),\text{with}{E}_p=\frac{{\left(I_{\mathit{pvp}}^p-I_{\mathit{ncp}}^p\right)}^2}{2{\sigma }_{\mathit{ncp}}{\sigma }_{\mathit{pvp}}}.$$ (5)

Similarly, location constraints from a normalized probabilistic atlas (PA) were implemented in $E_{\mathit{location}}(A)=-{\displaystyle \sum _{p\in P}}ln(S_p(p\mid O))$, where S_p represents the probability of p to belong to O. S_p was obtained by registering PA to the test images by a sequence of coarse-to-fine affine registrations.

E_boundary assigns penalties for 4D heterogeneity between two voxels p and q, with q∈N_p a small neighborhood of p. λ, μ and δ are constants and weigh the contribution from object/background, and the directionality of the graph at boundaries/shape, respectively (all set to value 0.5 for equal contributions). dist(p, q) is the Euclidean distance between p and q.

$$\begin{array}{l}{E}_{\mathit{boundary}}(A)=\mu \sum _{\{p,q\}\in N_p}{w}_{\{p\to q\}}+(1-\mu )\sum _{\{p,q\}\in N_p}{w}_{\{q\to p\}};\\ \mathit{Initialize}{w}_{\{p\to q\}}=w_{\{q\to p\}}=\{\begin{array}{ll}0,\hfill & {\mathit{ifA}}_p=A_q\hfill \\ exp\left(-\frac{\left|I_{\mathit{ncp}}^p-I_{\mathit{ncp}}^q\right|·\left|I_{\mathit{pvp}}^p-I_{\mathit{pvp}}^q\right|}{2{\sigma }_{\mathit{ncp}}{\sigma }_{\mathit{pvp}}}\right)\frac{1}{\mathit{dist}(p,q)},\hfill & \mathit{otherwise}\hfill \end{array};\\ IF\left((I_{\mathit{pvp}}^p-I_{\mathit{pvp}}^q)>{\sigma }_{\mathit{pvp}}OR(I_{\mathit{ncp}}^p-I_{\mathit{ncp}}^q)>{\sigma }_{\mathit{ncp}}\right)\mathit{THEN}{w}_{\{q\to p\}}=1;\mathit{ELSE}{w}_{\{p\to q\}}=1.\end{array}$$ (6)

The last condition in (6) penalizes transitions from dark (less enhanced) to brighter (more enhanced) regions considering image noise, to correct the edges of O. This is an intrinsic attribute of medical data (e.g. the abdominal muscles are darker than O). Additional penalties were implemented from the seeds for O and B from I_o and I_b.

Shape constraints were introduced using Parzen windows [11] estimated from the reference liver shapes from the 10 non-contrast CT data. First, the result of the 4D convolution (L) was used to align the shape references using scaling, rotation and the location of the centroids. An asymmetric normalized dissimilarity measure D was used to avoid the bias introduced by L; H is the Heaviside step function

$$D(s_1,s_2)=\int {(H(s_1)-H(s_2))}^{2}H(s_1)dx/\int H(s_1)dx.$$

The Parzen shape probability PS of s given n shape references was calculated [3] to encourage cuts that minimize the shape dissimilarity

$$\begin{array}{l}PS(s)={\sum }_{i=1}^{n}exp(-D(s,s_i)/2{\sigma }^2)/n;{\sigma }^2={\sum }_{i=1}^n\underset{j\ne i}{min}D(s_j,s_i)/n;\\ \text{then}{E}_{\mathit{shape}}(A)=\delta \sum _{\{p,q\}\in N_p}{v}_{\{p\to q\}}+(1-\delta )\sum _{\{p,q\}\in N_p}{v}_{\{q\to p\}};\text{with}\\ v_{\{p\to q\}}=v_{\{q\to p\}}=\{\begin{array}{ll}0,\hfill & if{A}_p=A_q\mathit{orPS}{(s)}^p=PS{(s)}^q\hfill \\ max(PS{(s)}^p,PS{(s)}^q)/\mathit{dist}(p,q),\hfill & \mathit{otherwise}\hfill \end{array};\\ IF\left(PS{(s)}^p>PS{(s)}^q\right)\mathit{THEN}{v}_{\{q\to p\}}=1;\mathit{ELSE}{v}_{\{p\to q\}}=1.\end{array}$$ (7)

We compared results obtained after the 4D convolution to those achieved using intensity-based 4D GC, and after including shape and location correction. The influence of patient specific versus population (historic) statistics on the accuracy of organ segmentation was also analyzed. We computed the Dice coefficient, volume error, root mean square error, and average surface distance. Non-parametric statistical tests (Wilcoxon paired test) were performed to assess the significance of segmentation improvement at different steps of the algorithm at 95% confidence interval.

3 Results

Quantitative results from applying our method to the segmentation of liver, spleen and kidneys are shown in Table 1 at different stages of the algorithm. Figure 2 presents a typical example of liver, spleen and kidneys segmentation. Another example is shown in 3D in Figure 3 along with the errors between manual and automated segmentations.

Table 1.

Statistics (mean±std) for the liver, spleen, left kidney and right kidney segmentation results from data of low resolution (5mm slice thickness). Columns present the Dice coefficient (DC), volume estimation error (VER), root mean square (RMSE) error and average surface distance (ASD). 4D C represents the convolution, GCI is GC based solely on image intensity (including 4D appearance and enhancement) and 4D GCSL includes shape and location constraints. Highlighted cells mark the organs where a significant improvement was obtained relative to the previous step of the segmentation algorithm (p<0.05).

	ORGAN	DC (%)	VER (%)	RMS (mm)	ASD (mm)
4D C (Historic Data)	LKidney	88.7±3.7	10.9±8.9	2.3±0.4	1.1±0.3
	RKidney	89.6±3.4	13.6±6.8	2.1±0.5	1.1±0.3
	Spleen	79.9±10.1	14.9±16.9	4.5±1.9	2.7±1.7
	Liver	89.1±3.7	7.3±4.6	6.7±1.5	3.4±1.0
4D GCI (Patient Data)	LKidney	92.6±2.4	5.4±6.9	1.8±1.2	0.8±0.6
	RKidney	92.8±1.9	5.6±5.8	1.8±0.8	0.8±0.4
	Spleen	89.6±2.7	11.4±6.9	3.0±1.4	1.5±0.9
	Liver	94.0±1.2	6.2±2.8	4.4±2.0	1.8±0.7
4D GCSL (Patient Data)	LKidney	91.9±2.4	4.5±4.6	1.7±0.5	0.8±0.3
	RKidney	92.6±1.3	5.2±2.9	1.7±0.4	0.8±0.3
	Spleen	90.7±1.4	8.2±5.0	2.2±1.0	1.2±0.5
	Liver	94.9±0.8	4.1±2.0	3.4±1.8	1.4±0.4

Figure 2.

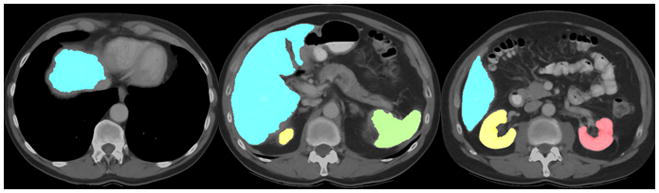
A typical example of liver (blue), spleen (green), right kidney (yellow) and left kidney (red) automated segmentation on 2D axial views of the CT data.

Figure 3.

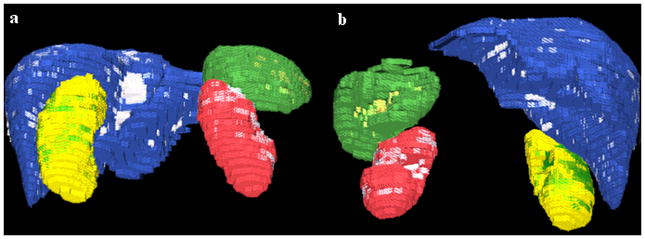
3D images of the automatically segmented abdominal organs; (a) is a posterior view and (b) an anterior view. The liver ground truth is blue with segmentation errors in white; spleen is green with errors in yellow; right kidney is yellow with errors in green; left kidney is red with errors in white. The pixilation is due to image low resolution (5mm slice thickness).

The use of 4D graph-cuts (GC) improved the results significantly over those of the 4D convolution for all organs, as seen in Table 1. Employing shape and location information brought a further significant improvement for the segmentation of the spleen and liver. Significantly better segmentations by using patient specific data over historic data were noted for both kidneys (not shown in Table 1).

4 Discussion

We proposed a new formulation for a 4D graph-based method to segment abdominal organs from multi-phase CT data. The method extends basic graph cuts by using: 1) temporal acquisitions at two phases and enhancement modeling; 2) shape priors from Parzen windows; and 3) location constraints from a probabilistic atlas. Enhancement information allowed improving regional bias within tissues, thereby better modeling the biological properties. Location probabilistic priors, intrinsic to medical data, and shape information from the asymmetric computation of Parzen shape windows (to avoid shape bias) supplied additional constraints for the global optimization of the graph. A Parzen distribution was preferred as a non-parametric probability model that converges to the true density with increasing number of samples.

Livers, spleens and kidneys were segmented from multi-phase clinical data following the typical acquisition protocol of abdominal CT images. An automated initialization of the graph was employed. Historic data from a patient population were used to initialize the graph based on an adaptive 4D convolution. Then patient specific image characteristics were estimated for improved specificity and input into the directional graph. Results from image data with low spatial resolution showed overlaps over 90% and average surface distances less than 1.5mm for all organs.

The method avoided the inclusion of heart segments in the segmentation of liver, but had the tendency to underestimate organ volumes, in particular that of the spleen. Parts of the inferior vena cava may be erroneously segmented in the mid-cephalocaudal liver region, especially when contrast enhancement is low, and represent one of the sources of error in the liver segmentation (Figure 3). Partial volume effects (low image resolution), small registration errors, and the estimation of object and background distributions may also contribute to undersegmentation. Results are expected to be superior on data with high spatial resolution.

As expected, using graph cuts based only on intensity significantly improved the segmentation of all four abdominal organs over the 4D convolution. However, moving from historic to patients specific statistics only improved the segmentation of kidneys, probably due to the prevalence of liver and spleen statistics in the object (O) histogram. Optimizing the graph with shape and location contraints brought a significant improvement only in the segmentation of spleen and liver, as kidneys, already well segmented at the previous step of the algorithm due to strong image contrast at edges from fast enhancement, vary less in shape. In the future we will include more shape/location references and variation to improve the segmentation.