Water in the polar and nonpolar cavities of the protein interleukin-1β

Abstract

Water in the protein interior serves important structural and functional roles, and is also increasingly recognized as a relevant factor in drug binding. The nonpolar cavity in the protein interleukin-1β has been reported to be filled by water based on some experiments and simulations, and to be empty based on others. Here we study the thermodynamics of filling the central nonpolar cavity and the four polar cavities of interleukin-1β by molecular dynamics simulation. We use different water models (TIP3P and SPC/E) and protein force fields (amber94 and amber03) to calculate the semi-grand partition functions term by term that quantify the hydration equilibria. We consistently find that water in the central nonpolar cavity is thermodynamically unstable, independent of force field and water model. The apparent reason is the relatively small size of the cavity, with a volume less than ∼80 ų. Our results are consistent with the most recent X-ray crystallographic and simulation studies, but disagree with an earlier interpretation of nuclear magnetic resonance (NMR) experiments probing protein-water interactions. We show that, at least semi-quantitatively, the measured nuclear Overhauser effects indicating the proximity of water to the methyl groups lining the nonpolar cavity can, in all likelihood, be attributed to interactions with buried and surface water molecules near the cavity. The same methods applied to determine the occupancy of the polar cavities show that they are filled by the same number of water molecules observed in crystallography, thereby validating the theoretical and simulation methods used to study the water occupancy in the nonpolar protein cavity.

1. Introduction

Water has long been known to play important structural and functional roles in proteins. In particular, buried water molecules may stabilize the structure of a protein by acting as a bridge between protein hydrogen bond acceptors and donors. In addition, water can participate in enzymatic functions, not only as a local dielectric but also as a mediator for proton transfer reactions. Despite the importance of water in biomolecular systems, studies of the interior hydration of proteins remain challenging for both experiment and simulation. On the experimental side, it often proves difficult to detect and characterize relatively small and mobile water molecules against a dominant background of bulk water.^1-6 On the computational side, interior water does not readily equilibrate with the bulk phase,⁷ and thus requires special treatment.^8-13 As a consequence of these challenges, important detail is often lacking in the many biological processes thought to involve structural water. These challenges are highlighted best by the interior hydration of interleukin-1β (IL-1β), with sharply conflicting results between different experiments,^14-20 as reviewed recently by Matthews and Liu,⁶ and between different simulations.^8,21-23

IL-1β is an immunomodulator with wide-ranging biological activities, including the stimulation of B-lymphocyte proliferation and of interleukin-2 and c-jun transcription. The 17 kDa protein IL-1β resembles a tetrahedron, formed by 12 β-strands arranged in three pseudo-symmetric topological units, each comprising 5 β-strands of which two are shared between units. IL-1β has a central nonpolar cavity that is large enough to potentially hold up to four water molecules (Figure 1), and four smaller polar cavities. The hydration of the polar cavities is well characterized by both crystallography^14-17,20 and NMR.^3,24 Each polar cavity contains at least one water molecule involved in bridging backbone hydrogen bonding interactions. But there has been some controversy about the presence of water molecules in the central nonpolar cavity and their thermodynamic stability. Four independently determined crystal structures^14-17 did not show the presence of any water molecules within the central nonpolar cavity. The absence of water may not seem entirely surprising, as atoms with root-mean-square fluctuations >1 Å (with crystallographic B factors >80 Ų) will make a negligible contribution^6,25 to Bragg reflections at resolutions higher than 4.5 Å. Since conventional high-resolution crystallography neglects data beyond 6-10 Å, one would not necessarily expect to detect disordered water molecules within the nonpolar cavity. NMR studies using 2D ¹²C-filtered H₂O-nuclear (NOE) and rotating frame (ROE) Overhauser enhancement-¹H-¹³C heteronuclear single quantum coherence spectroscopy demonstrated the existence of 95 cross-peaks that could be unambiguously attributed to direct through-space interactions with bound water.¹⁸ Of these, 65 involved protons in close proximity (<4 Å) to 10 crystallographically conserved water molecules participating in bridging backbone hydrogen bonds. 26 NOE/ROEs to water were also observed for the methyl groups of Leu10, Leu18, Leu26, Leu26, Leu69, Leu80, Ile122 and Val132 and some associated methine and methylene groups. These residues line the central nonpolar cavity and their side chains are directed towards the interior of the cavity. 24 of these 26 protons are further than 4 Å from individual crystallographically conserved water molecules, and 16 are further than 5 Å. It was therefore concluded that the NOE/ROEs involving the 8 methyl-containing residues might arise from disordered water within the central nonpolar cavity.¹⁸ However, it has to be emphasized that while NMR can demonstrate that a proton is close to water it cannot ascertain directly the exact location of that water molecule.

Figure 1.

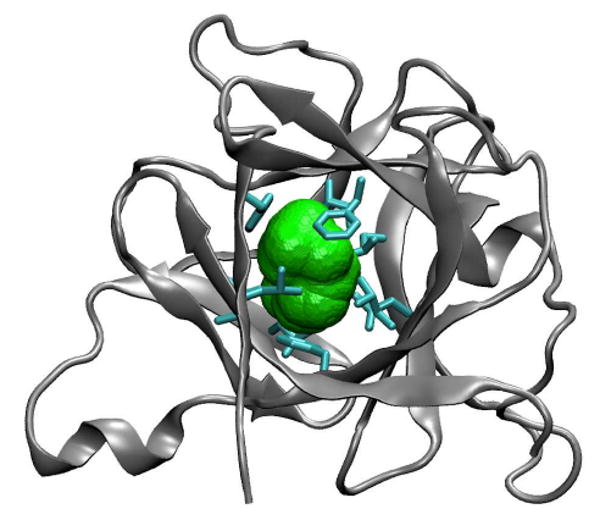
Structure of IL-1β (PDB code 6I1B²⁴), with nonpolar residues (cyan) lining the central cavity (green). For a spherical probe of radius 1.4 Å, the volume accessible to the probe center is ∼10 ų, and the volume covered by the probe sphere (shown in green) is ∼140 ų. In the most recent crystal structure of IL-1β by Quillin et al.²⁰ (PDB code 2NVH) the volume covered by a probe sphere of 1.4 Å radius is ∼40 ų. In the other crystal structures,¹⁴-¹⁷,⁴⁷ the volume varies between ∼45 and ∼80 ų. In the amber03/TIP3P MD simulations with occupancy N=0, starting from the NMR structure 6I1B,²⁴ the volume fluctuates about a mean of ∼80 ų. The larger cavity volume in the NMR structure 6I1B²⁴ is partly a reflection of the fact that it was refined before the use of compactness restraints.⁴⁸

Two alternative crystallographic approaches were taken to probe for the possible presence of water within the nonpolar cavity. An earlier study¹⁹ involved a theoretically based crystallographic phase technique in which the phases of the low resolution data were computed and iteratively refined on the basis of the existing high-resolution crystal structures. This analysis suggested that the central cavity was occupied by a water dimer with an occupancy of ∼70%, corresponding to an average density about half that of liquid water (i.e., the cavity could be regarded as either half full or half empty). A more recent study²⁰ made use of experimental phases derived by combining native and platinum multiwavelength anomalous dispersion data to circumvent issues arising from model bias and concluded that the occupancy of the solvent in the nonpolar central cavity is equal or close to zero. In contrast, the polar cavities in IL-1β were found to contain the expected number of ordered water molecules.^6,20

From early molecular dynamics studies Zhang and Hermans⁸ and Yin²⁶ concluded that the nonpolar cavity of IL-1β was empty. Somani et al.²² concluded from different MD studies that the central nonpolar cavity could stably accommodate four water molecules, which exist preferentially as clusters formed by hydrogen bonding between the water molecules and by interactions with the aromatic rings of the cavity walls. One and two water molecules are highly mobile and positionally disordered, as suggested previously by the NMR studies.²⁷ Using a Gaussian approximation for the energy distribution of cavity water Somani et al.²² calculated the excess chemical potential of water molecules as a function of the occupancy using the SPC model for water, and concluded that four water molecules are needed to hydrate the cavity in a thermodynamically stable manner for which the free energy of transfer is about -15 kJ/mol. According to their analysis, 1-3 water molecules are thermodynamically unstable in the central nonpolar cavity. In contrast, Oikawa and Yonetani²³ used thermodynamic integration and reported that the transfer free energy into the nonpolar cavity was unfavorable for occupancies ranging from 1 to 4 water molecules.

Clearly both the experimental and theoretical evidence for water within the nonpolar cavity of IL-1β is at best ambiguous. In this study we therefore set out to determine the free energies of transfer of water from the bulk phase into both the nonpolar and polar cavities of IL-1β using the methods developed by us earlier to study the hydration of cavities in the T4 lysozyme mutant L99A,¹² the thermostable protein tetrabrachion,²¹ and of water encapsulated in fullerenes and artificial cavities of varying polarity.^13,28 We use both the TIP3P²⁹ and SPC/E³⁰ models for water and find that the Gaussian approximation for the removal energy distributions of cavity water is not sufficiently accurate to determine reliable free energies of transfer from the excess chemical potential of cavity water. We also estimate the energy and entropy of transfer of water into the nonpolar cavity in IL-1β and find that although the energy of transfer of two or more molecules is favorable, the entropy of transfer is unfavorable to the extent that the free energy of transfer is also unfavorable for all cavity occupancies ranging from one to five water molecules. This is in contrast to the filling of the nonpolar cavity in tetrabrachion,²¹ where the energy-entropy balance is tilted in favor of a stable cluster of 7-8 water molecules even at elevated temperatures. We also find that the same methods applied to the four polar cavities in IL-1β confirm the presence of thermodynamically stable water molecules (with negative free energies of transfer) in agreement with the experimental X-ray results. In light of these simulation results, and by reinterpreting the earlier NMR data,¹⁸ we conclude that the nonpolar cavity of IL-1β is indeed “hydrophobic,” i.e., not significantly filled by water at ambient conditions.

2. Methods

Theory

Water exchange between the cavity and the bulk solvent is expected to be slow on the simulation timescale. To establish an equilibrium between the water-filled and empty states, we thus employ the semi-grand-canonical formalism used previously to study the interior hydration of lysozyme¹² tetrabrachion,²¹ and nonpolar cavities²⁸ as described in ref 13. In short, we consider a spherical observation volume V that covers the cavity of interest. The probability p(N) of observing exactly N water molecules in the volume V then satisfies

$$\frac{P(N+1)}{P(N)}=\frac{\rho V{e}^{\beta {\mu }_{\text{bulk}}^{\text{ex}}}}{N+1}{\langle e^{-\beta (U_{N+1}-U_N)}\rangle }_N,$$ (1)

where $z=\rho e^{\beta {\mu }_{\text{bulk}}^{\text{ex}}}$ is the activity of water, ρ is the number density in the bulk, and ${\mu }_{\text{bulk}}^{\text{ex}}$ is the corresponding excess chemical potential, with β = 1/k_BT and T the absolute temperature and k_b Boltzmann's constant. The factor ${\langle e^{-\beta (U_{N+1}-U_N)}\rangle }_N\equiv exp(-\beta {\mu }_{N,N+1}^{\text{ex}})$ can be determined from a combination of test-particle insertion into the ensemble with exactly N water molecules in the cavity, and virtual particle-removal from a system with N+1 water molecules. Specifically, we use Bennett's method of overlapping histograms³¹ for the normalized distributions p_ins,N(ΔU) and p_rem,N+1 (ΔU) of particle insertion and particle removal energies ΔU = U_N+1 − U_N, respectively:

$$\frac{p_{\text{ins},N}(\Delta U)}{p_{\text{rem},N+1}(\Delta U)}=e^{\beta \Delta U}{\langle e^{-\beta (U_{N+1}-U_N)}\rangle }_N.$$ (2)

In a plot of ln (p_ins,N / p_rem,N+1) against ΔU, the intercept with ΔU = 0 gives the excess chemical potential of the confined water, $-\beta {\mu }_{N,N+1}^{\text{ex}}=ln{\langle exp[-\beta (U_{N+1}-U_N)]\rangle }_N$. Furthermore, we can test whether the confined water is in proper thermal equilibrium by verifying that the data lie on a straight line with slope β. This procedure is repeated for different values of N. From a combination of all the data, recursive application of eq 1, and normalization of P(N), we then build up the free energy as a function of the cavity occupancy. The difference in the Helmholtz free energy is ΔA_N = −k_BT ln P(N) / P(0) + pV_N,bulk, where the pV term is negligible here at ∼1 atm pressure.

If the binding energy distributions p_ins,N(ΔU) and p_rem,N+1 (ΔU) are sufficiently close to Gaussian, one can also estimate the factor 〈e^{−β(U_N+1−U_N)}〉_N from low-order perturbation theory.^22,32,33 Specifically, for a Gaussian, one obtains ${\mu }_{N,N+1}^{\text{ex}}\approx {\langle \Delta U\rangle }_N-\beta {\langle {\mathbf{\left(}\Delta U-{\langle \Delta U\rangle }_N\mathbf{\right)}}^2\rangle }_N/2$. However, in practice the binding energy distributions tend to be broad with non-Gaussian tails that contribute significantly to the average, for which empirical corrections have been suggested.^22,33

Molecular dynamics simulations

We performed three sets of molecular dynamics simulations with different force fields for the protein and different water models, combining amber94³⁴ and TIP3P water,²⁹ amber94 and SPC/E water,³⁰ and amber03³⁵ with TIP3P water. In all simulations, we used the Sander program in the Amber9 suite.³⁶ The time step was 1 fs in the amber94 simulations, and 2 fs in the amber03 simulation. Bonds involving hydrogen atoms were constrained with SHAKE.³⁷ In the amber03 simulation, the temperature was maintained at 300 K by using Langevin dynamics with a collision frequency of 2/ps; and the pressure was maintained at 1 bar using the Berendsen weak coupling algorithm³⁸ with a time constant of 1 ps. In the two amber94 simulations, the temperature and pressure were 298.15 K and 1 atm, maintained by a Berendsen thermostat and barostat, respectively.³⁸ The non-bonded real-space cutoff was set at 10 Å. Particle-mesh Ewald summation³⁹ was used to treat the long-range electrostatic interactions. For each of the different occupancy states of the nonpolar cavity, simulations were run for times between 9.8 and 12 ns (amber03), and for 5 ns (amber94).

In all simulations, we used the protein data bank (PDB) structure 6I1B as the starting structure, as obtained by solution NMR experiments.²⁴ The seven water molecules in the experimental structure were retained in all simulations (except when the hydration of the respective polar cavity was probed). In the amber03 simulations, the fully surface exposed His30 was protonated at the N_ε atom, resulting in an overall neutral protein. In the amber94 simulations, a neutralizing sodium ion was added to the solution, with His30 uncharged. The protein was solvated with 7338 water molecules in the amber94 simulations, and 4551 water molecules in the amber03 simulations.

To perform simulations with fixed numbers N of water molecules in the respective cavity of IL-1β, we employed two different strategies. In all simulations, appropriate numbers N of water molecules were initially taken from the bulk phase and placed into the cavity. The system was subsequently equilibrated for a few hundred picoseconds. In the amber94 simulations, if a water molecule escaped from the nonpolar cavity it was put back to the center, followed by additional equilibration. To prevent such water escape in the amber03 simulations, a restraining potential was added. This potential was flat up to a distance of 5 Å from the center of the cavity, and then rose quadratically. Only structures with water in the flat, unbiased part of the potential were considered for analysis. Cavity centers were defined through the geometric mean of nearby C_α atoms. For the large nonpolar cavity in the amber03 simulations, we used the C_α atoms of Leu10, Leu60, Phe112, Val132, and Phe146. In the amber94 simulations, the C_α atoms of Leu18, Leu26, Phe42, Leu69, Leu80, and Il122 were used in addition, together with a slightly larger radius of 6 Å defining the probe volume V.

Comparison to NMR NOE measurements

To compare our simulations of the hydrated IL to the NMR measurements of water-protein interactions, we used a simplified model in which we calculate an effective, NOE-weighted distance,

$$r_{\text{eff},i}=\langle {\left[{\sum }_{\alpha }{\sum }_j{r}_{i_{\alpha }j}^{-6}/3\right]}^{-1/6}\rangle ,$$ (3)

between the three protons α of methyl group i lining the nonpolar cavity, and the water protons j. The average is over the ensemble of simulation structures. For reference, we also evaluate these averages for different crystal structures (using the water oxygen and methyl carbon atoms instead of the unresolved protons) and the NMR structure with water. For an effective distance r_eff,i less than about 5 Å, we can expect an NOE signal in the NMR measurements. This simplified analysis ignores the dynamics of the proton-proton distance vectors, and the coupling between the protons. For a single proton-proton pair involving a cavity methyl proton and an NMR-detected water, we found that inclusion of dynamics⁴⁰ reduced the NOE intensity by less than a factor of two. With couplings between the large number of protons at the surface expected to partly compensate this effect, we here use only the simplified estimate involving the static ensemble.

3. Results and Discussion

Nonpolar cavity

First we verify that the water molecules in the nonpolar cavity are properly equilibrated. By comparing the distributions of insertion energies from simulation structures with N water molecules in the cavity to the distributions of removal energies with N+1 water molecules, we can directly test whether the different simulations are consistent with each other, and whether the energies are indeed Boltzmann distributed. Figure 2a shows the distributions of water insertion and removal energies for N=0 and 1, respectively. We find that p_rem,1(ΔU) agrees very well with $p_{\mathit{\text{ins}},0}(\Delta U)exp\left[-\beta (\Delta U+{\mu }_{0,1}^{ex})\right]$, as required by eq 2, over virtually the entire range of overlap (with p_ins,0(ΔU) varying over more than six orders of magnitude). We find similar agreement for the pairs of insertion and removal distributions. As shown in Figure 2b, the logarithm of the ratio of insertion and removal probability distributions is a linear function of the energy ΔU, with the required slope of β. From the intercept of the linear fits with fixed slope β, we extract the excess chemical potentials ${\mu }_{N,N+1}^{ex}$ entering into eq 1 for the ratio of the occupancy probabilities.

Figure 2.

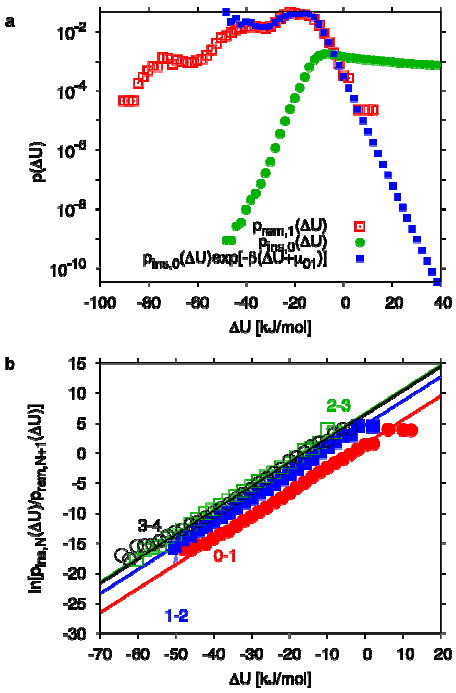
Distribution of water insertion and removal energies. (a) Distribution of removal energies p_rem,1(ΔU) (open squares) and insertion energies p_ins,0(ΔU) (circles), and reweighted distribution $p_{\mathit{\text{ins}},0}(\Delta U)exp\left[-\beta (\Delta U+{\mu }_{0,1}^{ex})\right]$ (filled squares), obtained from amber03. (b) Logarithm of the ratio of the normalized distributions of insertion and removal energies for transitions between N=0 and 1 (filled circles), 1 and 2 (filled squares), 2 and 3 (open squares), and 3 and 4 (open circles). Also shown are straight-line fits with fixed slope β, and intercept $\beta {\mu }_{N,N+1}^{ex}$.

By combining the results for N=0, 1, 2, 3, and 4, followed by normalization, we obtain the occupancy probabilities P(N). From the P(N), we calculate the water transfer free energies. Figure 3 shows the resulting free energies ΔA_n of transferring N water molecules from bulk into the nonpolar cavity of IL-1β, defined as ΔA_N = −k_BT ln P(N) / P(0), ignoring a small pV term.⁴¹ The results for the different combinations of protein force fields and water models are consistent, with only modest force-field associated differences in the transfer free energy. All simulations show that filling the nonpolar cavity of IL-1β with water is thermodynamically unfavorable. The highest free energy penalty of about 5-6 k_BT is encountered by the first water molecule entering the cavity. This penalty is large despite the fact that the first water molecule is relatively free to move around in the cavity and can even form transient interactions with a structural water molecule that contribute to the low-energy shoulders in the distribution shown in Figure 2a. Subsequent water molecules face lower costs of about 2 k_BT each, reflecting the fact that they can form hydrogen bonds with the water molecules already in the cavity. Overall, transferring water molecules into the nonpolar cavity is uphill in free energy over the entire range of occupancies considered. We have also performed simulations with N=5, and found this filling state to be unstable. Therefore we conclude that according to all simulation models, the nonpolar cavity of IL-1β is predicted to be empty.

Figure 3.

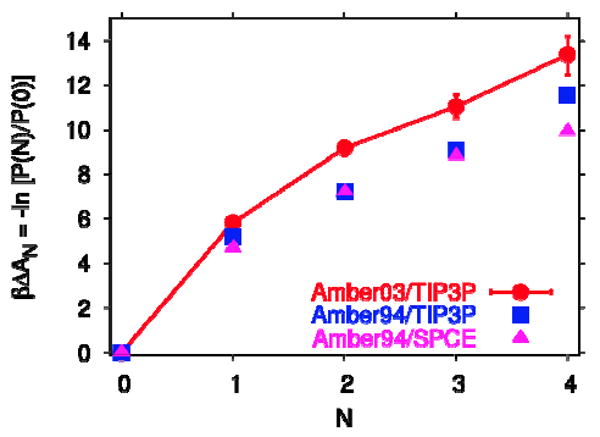
Free energy ΔA_n of transferring N water molecules from bulk into the nonpolar cavity of IL-1β, obtained from the logarithm of P(N)/P(0). Results are shown for simulations using the amber03 force field with TIP3P water (circles), amber94 with TIP3P water (squares), and amber94 with SPC/E water (triangles). Lines are guides to the eye.

Is this due to unfavorable energy or entropy of transfer into the nonpolar cavity? To answer this question we estimate the energy of transfer from the difference in the energy required to remove all N water molecules collectively from the cavity (N=1 to 4) and the energy of N water molecules in the bulk phase:²¹

$$\Delta U_N/N\approx {\langle U_{\mathit{\text{rem}},N}\rangle }_N/N-{\langle U_{\mathit{\text{rem}},1}\rangle }_{\mathit{\text{bulk}}}/2.$$ (4)

The first average is over the removal energy of the entire N-water cluster from the cavity, and the second average is over the removal energy of a single water molecule from the bulk phase. This relation is correct in the absence of reorganization energies, which is a reasonable assumption for nonpolar cavities. From the difference between the transfer energy and the transfer free energy we obtain the transfer entropy, ΔS_N = (ΔU_N − ΔA_N) / T. Our results are displayed in Figure 4 which show that although filling with 1 and 2 water molecules is energetically unfavorable, it becomes energetically favorable when the occupancy N is increased to 3 and 4, likely due to increased hydrogen bonding between the water molecules in the cavity.²⁸ The favorable energy at the higher cavity occupancy is outweighed by the unfavorable entropy and overall the free energy of transfer is always positive, as shown in Figure 3. A four-molecule water cluster is actually observed in our simulations (Figure 8) and by others, but in our study, unlike that of Somani et al.,²² this cluster is thermodynamically unstable at room temperature. A structurally similar four-molecule water cluster in the larger nonpolar cavity of tetrabrachion is also unstable at 298 K (see Table 2 of ref 21), but much less so, by about 1 k_BT instead of >10 k_BT here. Although the energies of transfer per water molecule are comparable (about -5.7 vs -5.2 kJ/mol here), the corresponding entropy of transfer into the nonpolar cavity within tetrabrachion is less negative (-2.31 k_B vs. -5.15 k_B) because the greater cavity size results in larger translational and rotational entropy of the water cluster. This comparison illuminates the entropic influence of cavity size on the free energy of water transfer into a nonpolar cavity and illustrates the fine balance between energy and entropy in determining the conditions of thermodynamic stability of water in nonpolar cavities.

Figure 4.

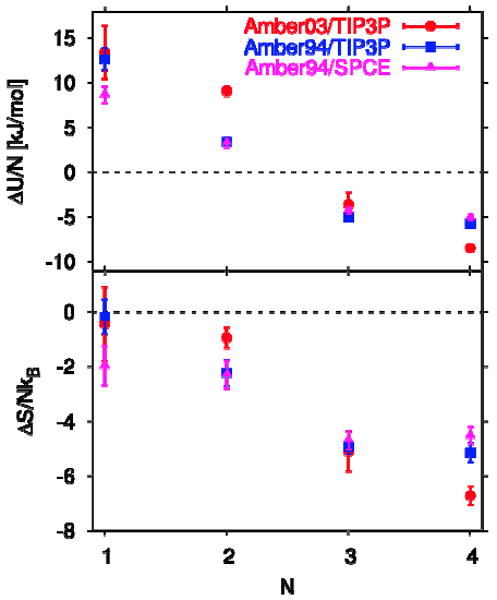
(a) Energy ΔU_n /N and (b) entropy ΔS_n /Nk_B per molecule of transferring N water molecules from bulk into the nonpolar cavity of IL-1β, estimated under the assumption of negligible protein reorganization energy.²⁶ Results are shown for simulations using the amber03 force field with TIP3P water (circles), and the amber94 force field with TIP3P (squares) and SPC/E water (triangles).

Figure 8.

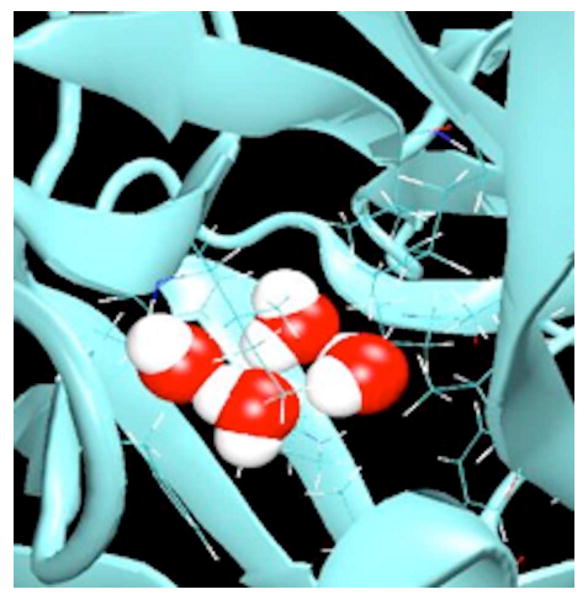
Hydrogen bonded tetramer formed by four water molecules in the central nonpolar cavity of IL-1β at 298 K.

Comparison to X-ray crystallography

Based on a careful examination of previous crystal structures, and a refinement of a new crystal structure with experimentally determined phases²⁰ Matthews and collaborators confirmed their earlier conclusion of an empty cavity,⁴² and also provided a rationale for the apparent electron density seen in an earlier study that used low-resolution data in the refinement.¹⁹ Our simulation finding of an empty nonpolar cavity is fully consistent with the crystallographic studies of Matthews and collaborators.^6,20

To extend this quantitative comparison to experiment, and to check that the simulation methodology is correct, we also studied the polar cavities of IL-1β. The crystal structure determined by Quillin et al.²⁰ (PDB code 2NVH) identifies four polar cavities, designated as 1 to 4, respectively (Figure 1 and Table 4 of ref 20), two cavities containing two water molecules each, and two containing one water molecule. As shown in Figure 5, our calculated transfer free energies of water into the polar cavities of the NMR structure are consistent with occupancies determined in the X-ray studies of Quillin et al.,²⁰ except that in cavity 4, where the most probable water occupancy number varies between one and two in two calculations based on simulations of 5 ns length, possibly due to small changes in protein conformation. The energies of transfer per water molecule (-22 to -90 kJ/mol in the different polar cavities, ignoring possible reorganization energies associated with changes in the protein structure in different hydration states) are an order of magnitude larger than they are for transfer into the nonpolar cavity, and so are the entropies of transfer (ΔS/Nk_B = -7 to -29), but here the compensation between energy and entropy works in favor of filling by one or two water molecules. In our simulations, the predicted hydration of both the polar and nonpolar cavities in IL-1β is thus fully consistent with the X-ray crystal data of Quillin et al.²⁰

Figure 5.

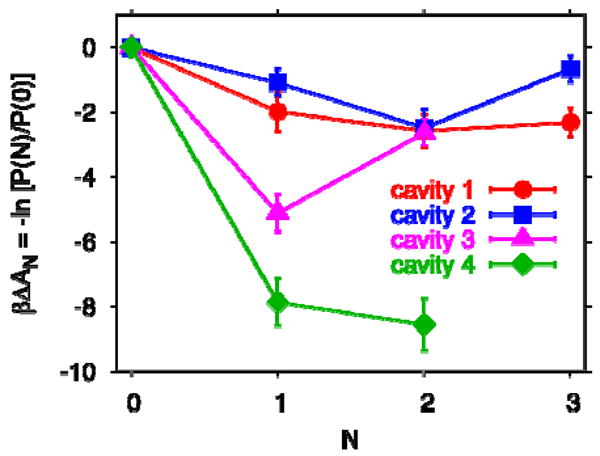
Free energies ΔA_n of transferring N water molecules from bulk into the polar cavities 1-4 of IL-1β, numbered according to Quillin et al.,²⁰ obtained from simulations using the amber94 force field with TIP3P water. Lines are guides to the eye.

Comparison to NMR

To compare our simulations to the NMR hydration study,¹⁸ we have calculated effective distances between the methyl protons of the residues lining the nonpolar cavity, and the water protons, including water in the polar cavities and in the surrounding solvent. Even with the nonpolar cavity being empty, we find that ∼90% of the effective proton-proton distances r_eff,i defined in eq 3 are at or below 5 Å (Figure 6). We have performed a similar analysis also on five different crystal structures with varying degrees of hydration. With proton positions not resolved, we used the distances between the methyl carbon and water oxygen atoms. For the MD simulation, the results obtained under this assumption are very similar to those for actual proton-proton distances (Figure 6). We find that the effective distances to water in the crystal largely follow those seen in the simulations, and that ∼60% of these distances are at or below 5 Å. For the NMR structure,²⁴ the effective distances are considerably larger, reflecting the fact that it contains only six water molecules buried in polar cavities, but no surface water. These results suggest that most, if not all, of the observed NOEs¹⁸ from water protons to methyl groups lining the cavity signals can be explained by interactions with nearby buried and surface water molecules, and likewise a significant fraction of the ROEs, which have a shorter range of less than ∼4 Å. We note, however, that if we use the ensembles with N=1 or 2 water molecules in the nonpolar cavity, instead of the structures with an empty cavity, the effective distance r_eff,i between water and the methyl groups i lining the cavity, as defined in eq 3, drops by about 0.5-1 Å, corresponding to a ∼4-fold increase in predicted NOE intensities.

Figure 6.

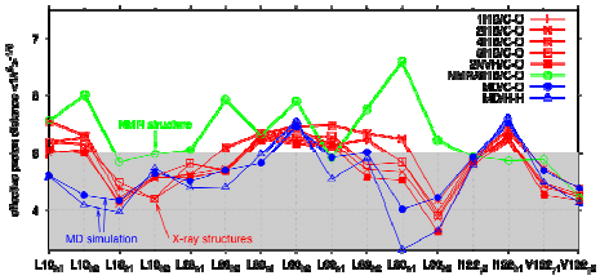
NMR NOE analysis. The effective distance between water protons and the methyl protons of nonpolar residues lining the cavity is shown for the MD simulations with an empty nonpolar cavity (blue) using actual proton distances (open triangles) and methyl carbon-oxygen distances (filled circles). Also shown are results for five different crystal structures (red; curves labeled by the corresponding PDB codes) and the NMR structure (green) with only six water molecules, calculated by using the methyl carbon-oxygen distances. Lines are guides to the eye.

Matthews et al.⁴² pointed out that the methyl carbons of Val-58 showed interactions with water, despite being buried. This was explained by Ernst et al.²⁷ by flexibility in the protein surface allowing water access. Indeed, in our simulations we find effective proton-proton distances of about 4 and 5 Å between the Val-58 methyl group and water, again consistent with the observed NMR water-methyl NOEs.¹⁸

Comparison to other simulation studies

The thermodynamics of transfer of water from the bulk phase into the nonpolar cavity of IL-1β has been studied by Zhang and Hermans⁸ and by Somani et al.²² and, more recently, by Oikawa and Yonetani²³ using molecular dynamics simulations. The methods used are different from our scheme based on the evaluation of the semigrand partition function for cavity water. From calculations of the energy of transfer, Zhang and Hermans⁸ concluded that the nonpolar cavity of IL-1β is insufficiently polar to contain water. Through studies of buried water in several other proteins, they suggest that a minimum of about -50 kJ/mol for the interaction energy of cavity water with the protein is necessary to drive a water molecule into a cavity, in rough agreement with our calculations for polar cavities. They maintain that the hydrogen bond network between water molecules in the cavity cannot compete with the network in bulk water, and that the contribution to the free energy of transfer from this source is small. In contrast, we found here and previously for tetrabrachion²⁶ that water-water interactions can be important factors driving the filling of large nonpolar cavities. Zhang and Hermans⁸ also assume that the entropy of transfer is small, even for polar cavities, which is not supported by our rough estimates for the polar cavities of IL-1β, and the free energy of transfer of water into the cavity is therefore dominated by the corresponding energy. Following these arguments, all nonpolar cavities in proteins, including IL-1β, would be empty, in contrast to the experimental⁴³ and computational findings for tetrabrachion.²⁶

In contrast to Zhang and Hermans⁸, Somani et al.²² predict that the cavity of IL-1β is filled by water. Somani et al.²² studied the transfer of one to four water molecules (N= 1 to 4) into the nonpolar cavity of the 9ILB¹⁹ structure of IL-1β, and found that up to 3 water molecules are thermodynamically unstable in the cavity, but that the addition of a fourth shifts the transfer free energy from unfavorable (positive ΔA_n) states to a favorable one (negative ΔA_n). Their analysis is based on the assumption that the binding energies of cavity water are Gaussian. We find that in the nonpolar cavity of IL-1β that a single Gaussian is a rather poor approximation (Figure 7), in particular in the high-energy tail most relevant for the transfer free energy.³² For a more accurate estimate, a multistate Gaussian description would be needed.⁴⁴ We also find some differences between the binding-energy distributions displayed in Figure 8 of ref 22 and ours, especially for N=1 (single occupancy). Somani et al.²² calculated an “excess chemical potential” μ^ex of cavity water from the average binding energy 〈u〉_N of a single water molecule in a cavity with N water molecules, and the variance ${\sigma }_N^2$ of u, ${\mu }^{\text{ex}}=16.7\text{kJ}/\text{mol}+{\langle u\rangle }_N+0.5{\sigma }_N^2/k_{B}T$. The first term in this expression is an ad-hoc correction factor corresponding to the free energy of transferring a hard sphere from an ideal gas into water, with a diameter of 2.7 Å, roughly matching the size of a water molecule. For the transfer free energy ΔA_n, in our notation, they then use $\Delta A_N/N={\mu }^{ex}-{\mu }_{\mathit{\text{bulk}}}^{ex}$. This expression for the transfer free energy of cavity water ignores the fact that the transfer is sequential, and that the Gaussian formula should thus be applied for the steps from 0 to 1, from 1 to 2, etc.; and it also assumes a constant “entropic” term of 16.7 kJ/mol that entirely ignores the size of the cavity. Whereas a Gaussian approximation can under some circumstances be used to approximate the Boltzmann average in eq 1 and 2, −kT ln〈exp[−β(U_N+1−U_N)]〉_N ≈ 〈U_N+1 − U_N〉 − βσ²/2, it has to be applied sequentially (i.e., for N=0→1, 1→2, etc.) and with the volume-dependent prefactor given in eq 1. We therefore conclude that the finding of a 4-water filled cavity in IL-1β is likely based on incorrect assumptions.

Figure 7.

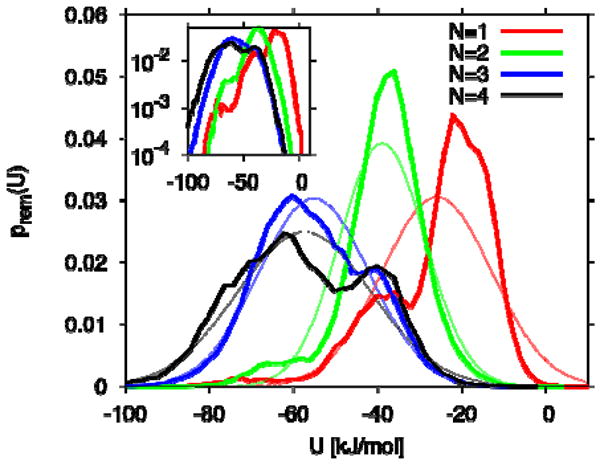
Distribution of removal energies for water in the nonpolar cavity of IL-1β. Results are shown for N=1 to 4 (thick lines; curves peaking from right to left). Thin lines show the corresponding Gaussian distributions. The inset shows the distributions on a logarithmic scale.

Very recently, Oikawa and Yonetani²³ evaluated the transfer free energy of TIP3P water into the nonpolar cavity of IL-1β, represented by both rigid and unrestrained models for the 9ILB¹⁹ structure of this protein. By using the method of Roux et al.⁹ and thermodynamic integration they calculated the free energy difference between a cavity filled with N water molecules and an empty one. A harmonic restraint on cavity water to prevent expulsion from the cavity was used, similar to the flat-bottomed potential used in some of our simulations. The free energies of transfer are positive (unfavorable) and in qualitative agreement with our calculations for the unrestrained 6I1B structure of the protein. Flexibility in the protein exposes polar groups and embedded water near the cavity walls, thereby increasing cavity polarity and transient hydrogen bond formation. Consistent with this interpretation, we also obtain conformations with low water removal energies, even in the singly occupied nonpolar cavity (Figures 2a and 7). These interactions reduce the free energies of transfer, but the differences are small for N=1. At higher occupancies (N≥2), local expansion of the cavity is a likely additional effect that explains the more favorable transfer free energies compared to a rigid protein. But despite these contributions, their main conclusion is that the transfer free energy of water into the nonpolar cavity of IL-1β is unfavorable for all reported occupancies from N=1 to 4. Oikawa and Yonetani do not report data for the transfer of one and two water molecules (N=1 and 2) into the cavity of their unrestrained model of the 9ILB¹⁹ structure of IL-1β since the water molecules apparently left the cavity during the MD simulations despite the restraining potential employed, unlike cavity water in the rigid model (see Figure 4 of ref 23, but note a possible inconsistency in the caption, with the figure suggesting that water escapes from N=2 and 3, not N=3 and 4).We have obtained data for all occupancies from N=1 to 4, by either returning ejected water back into the cavity followed by re-equilibration, or by applying a restraining potential at the edges, as stated earlier. The free energies of transfer of one and four water molecules into the nonpolar cavity of the unrestrained model (9ILB¹⁹; see Figure 4 of ref 23) are ∼16.7 kJ/mol (∼6.7 k_BT) and ∼46 kJ/mol (∼18.4 k_BT) respectively, and are larger by about 2 k_BT per cavity water molecule than our calculations for the unrestrained 6I1B structure (see Figure 3). These differences are more likely due to differences in theoretical methodology rather than differences between the crystal (9ILB¹⁹) and NMR (6I1B²⁴) structures of IL-1β. In particular, the use of thermodynamic integration to “grow in” water makes it difficult for a gradually inserted water molecule to exchange position with already present water molecules, and sample the entire cavity. As a result, one would expect a bias toward more unfavorable transfer free energies, which would explain the differences to our work. Nevertheless, the main conclusion by Oikawa and Yonetani²³ of an empty cavity in IL-1β is fully consistent with our findings.

The thermodynamic instability of water in the nonpolar cavity in IL-1β can be traced to its relatively small volume. Already for the transfer of a single water molecule into the empty cavity, we estimate a slightly unfavorable (negative) entropy (Figure 4B). Likely reasons are, first, that the water-accessible volume of the cavity is only about twice the partial molar volume of bulk water; and, second, that the water molecule in the cavity can make transient interactions with one of the structural water molecules, as evidenced by the low-energy shoulders in the removal energy distribution Both effects are enhanced as additional water molecules form hydrogen-bonded clusters that fill up the small cavity volume. The observed decrease in the relative entropy of transfer (Figure 4) with occupancy is thus the result of a reduction in translational entropy, as the remaining available volume shrinks with increasing occupancy, and of a reduction in both translational and rotational entropy, as water molecules become increasingly localized through hydrogen bonding and cluster formation in the densely filled cavity. A similar decrease in the entropy was observed for the nonpolar cavity in tetrabrachion, where we also tested the approximation eq 4 used to calculate the transfer energies and entropies.²¹ The somewhat more positive (favorable) entropies in tetrabrachion are a result of its significantly larger cavity size compared to IL-1β.

Dunitz⁴⁵ has provided rough bounds on the entropy of water molecules filling a cavity, -3.5 < Δs_n/Nk_B < 0. However, these numbers are based on heuristic arguments and should be taken with care. For one, the estimated bounds apply to cavities that are actually filled at equilibrium under ambient conditions, whereas here we probe the transfer into a cavity that turns out to be mostly empty at equilibrium based on our calculations. Furthermore, the entropy of transfer will depend sensitively on a number of factors, in particular the size, polarity, and filling state of the cavity. Enthalpy-entropy compensation arises from trade-offs between favorable energies of interaction with the protein, or with water molecules already in the cavity, and associated losses in entropy. Consistent with our simulation results for tetrabrachion²¹ and for IL-1β, one would in particular expect the entropy per water molecule to go down as additional water molecules enter the cavity and form new hydrogen bonds that restrict their translational and rotational movement.

The energies of transfer from the bulk phase into the nonpolar cavity of IL-1β are unfavorable (positive) for single and double occupancy (Figure 4). With the entropies of transfer being negative, single and double occupancy states are therefore thermodynamically unfavorable. Although the energies of transfer of three and four molecules from the bulk phase into the cavity are favorable (negative), they are not large enough to surmount the unfavorable entropies of transfer. In contrast, for the nonpolar cavity of tetrabrachion,²¹ comparable energies of transfer proved sufficient to induce filling because the entropic penalty was smaller for the cavity with a significantly larger volume compared to the one in IL-1β.

4. Conclusions

We conclude from our molecular dynamics simulations and theoretical analysis that water molecules in the central cavity of IL-1β are thermodynamically unstable. The transfer free energy from the bulk phase into the central cavity of IL-1β is positive and increases monotonically with the number N of water molecules in the cavity over the entire range, up to N=4. This result is independent of the force field for protein and water used. The calculated free energy penalty for hydration is substantial. So while it is possible that the energetics could be altered by the inclusion of polarizability in the simulation force field, we do not expect such changes to be large enough to alter the main conclusion. Nevertheless, it will be interesting to reexamine the problem with simulation models in which the interactions between water and the aromatic and aliphatic side chains lining the cavity are treated more accurately than in the fixed-charge force fields used here. Our finding of an empty nonpolar cavity in IL-1β is consistent with the experimental studies of Quillin et al.²⁰ and is in qualitative agreement with simulations carried out independently by Yin²⁶ and by Oikawa and Yonetani.²³ At least semi-quantitatively, we can also explain the observed NOE and ROE NMR couplings between the protons of nonpolar groups lining the cavity and water²⁷ as arising from interactions with buried and surface water. Besides actual water penetration, additional contributions to the measured couplings²⁷ could arise from transient excursions of water molecules in the polar cavities of the protein.

The apparent reason for the absence of water in the nonpolar cavity of IL-1β is its relatively small size of between 40 and 80 ų in different X-ray structures, ∼80 ų in our simulations, and ∼120 ų in an NMR structure (Figure 1). Even the somewhat larger nonpolar cavity in T4 lysozyme, with a volume of ∼170 ų, was previously found to be empty at ambient conditions by both experiment and simulation,^12,46 where filling with water was observed only at elevated hydrostatic pressures of >1 kbar. In small nonpolar cavities, the loss of interaction energy with bulk water cannot be fully offset by the gains in entropy and in energy from water-cluster formation. We conclude from the simulations here of IL-1β, and before of T4-lysozyme^12,46 and tetrabrachion²¹ that nonpolar cavities in proteins are not stably hydrated if they can hold only about four water molecules. In contrast, the cavities of fullerenes, with their more densely packed carbon walls, were found to be stably hydrated by a four-water cluster.²⁸

Our results for the four polar cavities are also consistent with the experimental findings of Quillin et al.,²⁰ with one or two water molecules in each of them at equilibrium. Despite the large negative (unfavorable) entropy of transfer, filling is driven by the negative energy of transfer which is an order of magnitude larger per water molecule than it is for water transferred into the nonpolar cavity and much greater than the unfavorable contribution from the entropy of transfer.