Terminology for mass transport and exchange

Abstract

Virtually all fields of physiological research now encompass various aspects of solute transport by convection, diffusion, and permeation across membranes. Accordingly, this set of terms, symbols, definitions, and units is proposed as a means of clear communication among workers in the physiological, engineering, and physical sciences. The goal is to provide a setting for quantitative descriptions of physiological transport phenomena.

THE SET OF SYMBOLS is an extension of those proposed by Wood (11), Gonzalez-Fernandez(3), Zierler (12), Kedem and Katchalsky (5), and Bassingthwaighte et al. (1). The extensions provide a set of symbols common to studies of transcapillary and cellular exchange and indicator-dilution studies. The rationale is to provide a self-consistent set of symbols covering broad aspects of circulatory flows, hydrodynamics, transcapillary and membrane transport. As the various previously rather separate aspects of these fields become intermeshed, the size of the required sets of symbols has enlarged to a point where the “standard” symbol for one group of users has a quite different “natural” meaning to another. This problem has necessitated some arbitrariness, but we have attempted to subscribe to the dominant usage so as to minimize changes in habits.

Care has been taken to provide each term with 1) a name, 2) a definition in words (and sometimes equations), 3) a unique symbol whenever possible, and 4) units mainly in centimeter-gram-second system but with some translation to approved International System of units (SI). Physical constants are listed separately.

An important feature of this list is the provision of operational terminology for the general description of the behavior of linear stationary systems. The use of the time-domain impulse response or transport function, h(t), etc., follows from the work of Stephenson (10), Meier and Zierler (6), and Zierler (12) and is reviewed by Bassingthwaighte and Goresky (2).

A system is diagramed in Figure 1. Most analysis is based on two fundamental assumptions, that the system is both linear and stationary. When both hold, superposition is applicable. In general, we also consider the system to be mass conservative; that is, indicator and solvent are neither formed nor consumed.

FIG. 1.

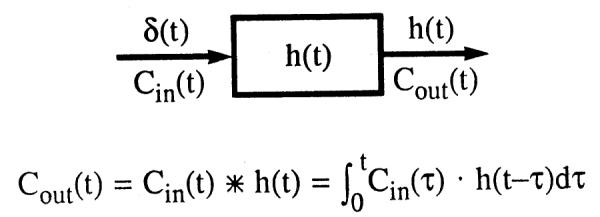
Block diagram of a linear stationary system. Response to ideal impulse input δ(t) at the entrance is h(t), the transport function. When input is of another form, C_in(t), then outflow response C_out(t) is the convolution of C_in(t) and h(t).

A linear system is one in which inputs and outputs are additive. Defining C_in(t), as concentration-time curve at the input to a segment of the circulation and C_out(t) as the concentration-time curve occurring in response to it at the outlet, the relationship is denoted by

$${\mathrm{C}}_{\text{in}}\left(t\right)\to {\mathrm{C}}_{\text{out}}\left(t\right)$$

Given a second pair with the same relationship ${\mathrm{C}}_{\text{in}}^{\prime }\left(t\right)\to {\mathrm{C}}_{\text{out}}^{\prime }\left(t\right)$, then in a linear system, these can be summed or multiplied by a scalar

$$\begin{array}{cc}\hfill {\mathrm{C}}_{\text{in}}\left(t\right)+{\mathrm{C}}_{\text{in}}^{\prime }\left(t\right)\to {\mathrm{C}}_{\text{out}}\left(t\right)& +{\mathrm{C}}_{\text{out}}^{\prime }\left(t\right)\text{or}\hfill \\ \hfill & k{\mathrm{C}}_{\text{in}}\left(t\right)\to k{\mathrm{C}}_{\text{out}}\left(t\right)\text{linearity}\hfill \end{array}$$

A stationary system is one in which the distribution of transit times through the system is constant from moment to moment; that is, flows and volumes are constant everywhere in the system. Stationarity implies that the response to a given input is independent of a shift in the timing of the input by an arbitrary time, t_o,

$$\begin{array}{ccc}\text{If}\hfill & \hfill {\mathrm{C}}_{\text{in}}\left(t\right)\to {\mathrm{C}}_{\text{out}}\left(t\right)\hfill & \hfill \hfill \\ \text{then}\hfill & \hfill {\mathrm{C}}_{\text{in}}(t_{\mathrm{o}}+t)\to {\mathrm{C}}_{\text{out}}(t_{\mathrm{o}}+t)\hfill & \hfill \text{stationarity}\hfill \end{array}$$

When the input system is an ideal unit impulse, the Dirac delta function, δ(t), then the output is the transport function, h(t). When the input is of general form, C_in(t), and h(t) is known, then the form of the output, C_out(t), can be calculated using the convolution integral given in Fig. 1.

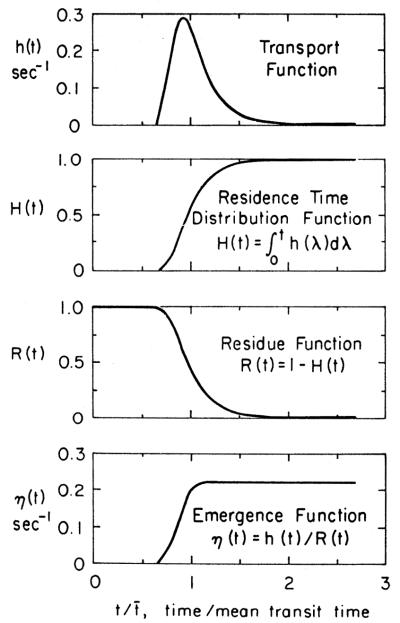
A probability density function h(x) or w(x) is a weighting function or a frequency function that gives the probability of occurrence of an observation or measure as a linear function of the quantitative measure, x. The sum of probabilities of all the observations is unity; therefore the units of the density function are fraction per unit of the measure [e.g., the transport function h(t)]. A typical form of h(t) for transport through an organ is given in Fig. 2, accompanied by closely related general functions.

FIG. 2.

Relationships between h(t), H(t), R(t), and η(t). Curve of h(t) is in this instance given by a unimodal density function having a relative dispersion of 0.33 and a skewness of 1.5. However, the theory is general and applies to h(t)s of all shapes. Tail of this h(t) curve becomes monoexponential and hence η(t) becomes constant.

Subscripts

A	Arterial
B	Blood
C or cap	Capillary, or the region of blood-tissue ex-  change
cell	Cell
D	Diffusive, or indicating a permeant tracer
ECF	Extracellular fluid
F	Flow or filtration
i,j	Indices in series or summations or elements  of arrays
in or i	Into or inside or inflow
ISF or I	Interstitial fluid space, the  extravascular extracellular fluid
m	Membrane
out or o	Out of or outside or outflow
P	Plasma
RBC	Red blood cell
R	Reference, nonpermeant tracer
S	Solute
T	Total
v	Venous
W	Water

Principal Symbols

a	Activity, molar; a = φC, an activity coefficient  times a concentration
A	Area of indicator concentration-time curve excluding recirculation $\text{A}={\int }_0^{\infty }\mathrm{C}\left(t\right)\mathrm{d}t,\text{mol}·s·l^{\mathrm{-1}}$
C	Concentration, mol/l; Cc(x, t) concentration  in the capillary plasma at position x at time  t (mol·1−1). Also [Na+] = sodium concentra-  tion. The relationship between an outflow  concentration-time curve Cout(t) and the  inflow curve Cin(t) in a stationary system is  given by the convolution integral: ${\mathrm{C}}_{\text{out}}\left(t\right)={\int }_0^{t}h(t-\tau ){\mathrm{C}}_{\text{in}}\left(\tau \right)d\tau ={\mathrm{C}}_{\text{in}}\left(t\right)\ast h\left(t\right)$ where τ  is a variable used in the integration. The  asterisk denotes convolution
C̄s	Concentration of solute, the average of the  concentrations on the two sides of a mem-  brane, molal, used in irreversible thermo-  dynamic equations. Note that this average  does not represent the mean concentration  within the membrane when both convection  and diffusion occur through a channel of  finite length
CV	Coefficient of variation, dimensionless. See  also RD; both are the standard deviation  divided by the mean of a density function
D	Diffusion coefficient, cm2·s−1; Do, in free  (aqueous) solution; Db for observed bulk  diffusion coefficient through tissue; Dcell for  intracellular; DI for interstitial
E	Electrical potential, volts; Em, membrane po-  tential; EN, “Nernst” potential, occurring  with a difference in concentration of an  ion on the two sides of a membrane, EN =  (RT/zF)loge(Cin,/Cout)
E(t)	Extraction, dimensionless, is the fraction of a  specific substance removed during transit  through an organ. The calculation may be  made relative to a reference substance that  remains in the blood or relative to the inflow  concentration. E(t) = [hR(t) – ho(t)]/hR(t)  and is the instantaneous apparent frac-  tional extraction of a permeating species,  subscripted D, relative to a nonpermeating  reference substance, subscripted R, at each  time t, calculated from paired outflow dilu-  tion curves. This differs from a steady-state  extraction, E, calculated from the arterio-  venous difference, E = (CA – Cv)/CA, for a  substance that is consumed during transor-  gan passage. E(tpeak) is the value of E(t)  obtained at the time of the peak of the curve  for the nonpermeating reference tracer,  hR(t). Emax is the maximum value of the  instantaneous extraction, E(t). Enet(t) is an  integral extraction, ${\int }_0^t(h_{\mathrm{R}}-h_{\mathrm{D}})\mathrm{d}\tau ∕{\int }_0^t{h}_{\mathrm{R}}\mathrm{d}\tau =({\mathrm{R}}_D-{\mathrm{R}}_{\mathrm{R}})∕(1-{\mathrm{R}}_{\mathrm{R}});$ when the  reference tracer has all emerged, then  Enet(t) = RD(t), the retained fraction of a  permeant solute
ECF	Extracellular fluid, interstitial fluid + plasma
f	Frictional coefficient, g·cm equals (g·cm2 s−1)/(cm·  s−1), following Spiegler (9)
fexcl	Excluded volume fraction, the fraction of sol-  vent in a defined space that is not available  to a particular solute, dimensionless
f i	Relative regional flow in the jth region of an  organ divided by the mean flow for the  organ per gram of tissue, dimensionless
F	Flow, cm3·s−1 or cm3·min−1
FB	Blood flow to an organ, cm3·g−1·min−1  (= F/W, where W = organ weight)
Fs, Fp	Flow of solute-containing mother fluid, cm3·  g−1·min−1. When solute is excluded from  red blood cells, Fs = FB(1 – Hct) = Fp, the  plasma flow. (In modeling analysis, this is  the flow of fluid containing solute available  for exchange.)
FER(t)	Fractional escape rate at time t for indicator  contained in a system regardless of time of  entry, s−1. With an impulse input, δ(t), then  FER(t) = η(t), the emergence function. In  general, FER = (dq/dt)/q = d logeq/dt,  where q is the system’s content of a sub-  stance and dq/dt = F[Cin(t) – Cout(t)]
h(t)	Transport function, fraction/unit time (s−1),  is the fraction of indicator injected at the  inflow at t = 0, arriving at the outflow at  time t. It is the unit impulse response, the  frequency function of transit times, or the  probability density function of transit  times. The transport function, h(t), has the  shape of the concentration-time curve that  would be obtained by flow-proportional  sampling at the output if indicator were  injected in ideal fashion into the inflow, i.e.,  across a cross section with indicator amount  at each point in proportion to local flow, as  defined by Gonzalez-Fernandez (3), and re-  circulation absent. Under such conditions  h(t) = F·C(t)/qo, where qo is the mass  injected at t = 0. Subscripting denotes re-  gion (e.g., A, V, or cap) or solute character-  istic (R for intravascular or D for permeant)
H(t)	Cumulative residence time distribution func-  tion (dimensionless) of a system; it repre-  sents the fraction of an ideally injected  tracer that has exited from the system since  t = 0. It is also the response to a step input.  Formally, $H\left(t\right)={\int }_0^{t}h\left(\tau \right)\mathrm{d}\tau =1-R\left(t\right)$,  where R(t) is the residue function
Hct	Hematocrit, the fraction of the blood volume  that is erythrocytes, dimensionless
ISF	Interstitial fluid, the extravascular extracel-  lular fluid
J	Flux, usually moles per unit surface area  of membrane per second, mol·s−1·cm−2.  Jnet 1→2 is net flux from side 1 to side 2. In  the notation of irreversible thermody-  namics the equations of Kedem and Katch-  alsky (5) and Katchalsky and Curran (4)  for water and solute transport across an  ideal membrane composed of infinitely thin  impermeant material pierced by aqueous  channels (the K and K membrane) are $$\begin{array}{cc}\hfill & J_{\mathrm{V}}=L_{\mathrm{p}}\Delta \mathrm{p}+L_{\mathrm{p}D}\Delta \pi \hfill \\ \hfill & J_{\mathrm{D}}=L_{\mathrm{D}\mathrm{p}}\Delta \mathrm{p}+L_D\Delta \pi \hfill \end{array}$$  where JD is a solute velocity relative to the  solvent velocity, Jv, which is in turn relative  to the membrane. [Although these expres-  sions are incomplete in that the forces on  the membrane, in effect a second solute,  should also be considered (8), they provide  an elementary conceptual approach to an  idealized system.] Jv and JD may be  properly regarded as flows rather than mass  fluxes
J V	Solvent velocity or volume flux per unit mem-  brane surface area relative to a membrane,  cm·s−1 or cm3 · s−1 per cm2 area $$J_{\mathrm{V}}=J_{\mathrm{W}}{\tilde{\mathrm{V}}}_{\mathrm{W}}+J_{\mathrm{S}}{\tilde{\mathrm{V}}}_{\mathrm{S}}\simeq J_{\mathrm{W}}{\tilde{\mathrm{V}}}_{\mathrm{W}}$$
J D	Solute movement relative to solvent, cm3 ·s−1  per cm2 surface area or cm·s−1. For the  Kedem-Katchalsky (K-K) ideal membrane  $J_{\mathrm{D}}=J_{\mathrm{S}}∕{\stackrel{‒}{\mathrm{C}}}_{\mathrm{S}}-{\tilde{\mathrm{V}}}_{\mathrm{W}}{J}_{\mathrm{W}}$ See JS
J W	Water flux across a membrane, mol·s−1·cm−2.  For the K-K membrane $J_{\mathrm{W}}=-{\tilde{\mathrm{V}}}_{\mathrm{S}}{J}_{\mathrm{S}}∕{\tilde{\mathrm{V}}}_{\mathrm{W}}$
J S	Solute flux across a membrane, mol·s−1·cm−2.  For the K-K membrane $J_{\mathrm{S}}={\stackrel{‒}{\mathrm{C}}}_{\mathrm{S}}(1-\sigma ){\mathrm{J}}_{\mathrm{V}}$.  Also $$\begin{array}{cc}\hfill J_{\mathrm{S}}∕{\stackrel{‒}{\mathrm{C}}}_{\mathrm{s}}& =(L_{\mathrm{p}}+L_{D_{\mathrm{p}}})\Delta \mathrm{p}+(L_{\mathrm{p}D}+L_D)\Delta \pi ,\text{or}\hfill \\ \hfill J_{\mathrm{S}}& ={\stackrel{‒}{\mathrm{C}}}_{\mathrm{S}}(1-\sigma )J_{\mathrm{V}}+\omega \Delta \pi \hfill \end{array}$$
k	Rate constant for an exchange process, usu-  ally s−1; k(C) is concentration-dependent  rate
k F	Filtration coefficient, cm3·s−1·cmm−2 (mmHg)−1;  kF = Lp. See Lp and also PF
K m	Michaelis constant, molar. For a reaction $$\mathrm{E}+\mathrm{S}\underset{k_{-1}}{\overset{k_1}{\leftrightharpoons }}\mathrm{ES}\stackrel{k_2}{\to }\mathrm{E}+\mathrm{P}$$  then Km = (k−1 + k2)/k1, which in the limit  where k2 << k−1 becomes the original appar-  ent dissociation constant, k−1/k1, which at  equilibrium = [E]·[S]/[ES]. (E, enzyme; S,  substrate; P, product)
l, L	Length, cm
L	Conductance (general) per unit area as in J =  LX; flux = conductance times driving force
L p	Pressure filtration coefficient or hydraulic  conductance; the flow of pure solvent across  a membrane per unit area per unit pressure  difference, e.g., cm·s−1(mmHg)−1; also, $L_{\mathrm{p}}=\tilde{\mathrm{V}}{P}_{\mathrm{F}}∕RT=k_{\mathrm{F}}$
L pD	Osmotic coefficient; the flow of solution across  a membrane per unit area per unit osmotic  pressure difference. Same units as Lp; also,  LpD = σLp
L Dp	Ultrafiltration coefficient; the conductance  for the hydrostatically driven flow of solute  relative to that of solvent, per  unit area per unit hydrostatic pressure difference. Same  units as Lp. By Onsager reciprocity, LDp =  LpD. (For an ideal semipermeable mem-  brane, σ = 1, ω = 0, and −LpD = Lp = LD =  −LDp)
LD	Coefficient for diffusional mobility per unit  osmotic pressure. Same units as LP. See ω  and P
M	Molarity, moles of solute per liter of solution.  Also mM, 10−3 M and μM, 10−6 M. (Molality  is moles of solute per kilogram of solvent.  The use of molal units gives consistency in  transient states; for example, the molal con-  centration of solute 1 is not changed by the  removal of solute 2, but the molar concen-  tration may be raised or lowered)
Mean	$\stackrel{‒}{X}$, the mean of a density function, ω(x), is  calculated by $$\begin{array}{c}\hfill \stackrel{‒}{x}={\int }_0^{\infty }x\cdot w\left(x\right)\mathrm{d}x/{\int }_0^{\infty }w\left(x\right)\mathrm{d}x\text{or}\hfill \\ \hfill =\sum _i{x}_i\cdot w\left(x_i\right)\Delta x_i∕\sum _{i}w\left(x_i\right)\Delta x_i\hfill \end{array}$$  Same as α1
ni	Same as α1 Moles of substance i in a solution. See mole  fraction xi
N	Number of observations or number of ele-  ments in a series, i = 1 to N
p	pressure, mmHg or Pa (1 Torr = 1 mmHg).  See osmotic pressure, π
P	Permeability coefficient for a solute traversing  a membrane, cm·s−1; equivalent to a diffu-  sion coefficient for a solute in a membrane  divided by the thickness. P = ωRT. P0, PL,  permeabilities at the arterial and venous  end of a capillary of length L, respectively.  P(x) for 0 < x < L for permeability at  position x. (Usually observed as a product,  PS, with the membrane surface area, S)
Pe	Peclet number, ratio of a convective to a dif-  fusive velocity, dimensionless
P F	Filtration permeability, $L_{\mathrm{p}}RT∕{\tilde{\mathrm{V}}}_{\mathrm{w}}$, cm·s−1.  [The conversion factor $RT∕{\tilde{\mathrm{V}}}_{\mathrm{w}}$ at 20°C, from  the experimental units for Lp or kF, is (18.36  mmHg·cm3·mol−1)/( 18 cm3·mol−1) equals  1.02 mmHg]
PS	Permeability-surface area product of a barrier,  cm3·g−1·s−1 or cm3·g−1·min−1. PScap for  capillary (the same as capillary diffusion  capacity), PScell for parenchymal cell
q	Mass, g or mol. q(t) is mass (or content of  tracer) in region or organ (at time t). q0,  mass of indicator injected at t = 0
r, R	Radius or radial distance, cm. RC, capillary  radius
RD	$\text{Relative dispersion}\left(\text{dimensionless}\right)=\mathrm{SD}∕\text{mean}=\sqrt{{\mu }_2∕{\alpha }_1}$. Same as coefficient of var-  iation
R(t)	Residue function (dimensionless) is the com-  plement of H(t), i.e., R(t) = 1 – H(t). It  represents the fraction of injectate in the  system at time t after an impulse input at  time zero, i.e., the probability of a tracer  residing in the system for time t or greater
S	Surface area. SC and Scell for capillary and cell  surface areas, cm2·g tissue−1
SD	Standard deviation = square root of the vari-  ance of a density function, ${\mu }_2^{1∕2}$. Also $\mathrm{SD}=\sqrt{{\alpha }_2-{\alpha }_1^2}$ (units are those of the independent variable)
SEM	Standard error of the $\mathrm{SD}=\sqrt{N}$, where  N = number of observations
t, Δt	Time, s; Δt is a finite time interval
$\stackrel{‒}{t}$	Mean transit time, s. $\stackrel{‒}{t}={\int }_0^{\infty }t\cdot h\left(d\right)\mathrm{d}t={\int }_0^{\infty }R\left(t\right)\mathrm{d}t$
t a	Appearance (a) time; the time at which the  first detectable indicator (or a concentra-  tion of, for example, 1% of the peak) passed  through the system
t 0	Zero time; midpoint of pulse injection for in-  dicator-dilution studies or beginning of con-  stant-rate injection
t peak	Time from injection to peak of indicator-di-  lution curve (modal time)
V	Volume, cm3 or ml; in a solution, $\mathrm{V}=\Sigma n_i{\tilde{\mathrm{V}}}_i$,  the sum of the products of the mole fraction  times the partial molar volume for each  contained species
Vregion	Anatomic volumes within regions of an organ,  i.e., VC, capillary; VI, interstitial fluid; Vcell,  parenchymal cells, cm3·(g tissue of the  organ)−1
vregion	Fractional regional volumes of distribution  available to a particular solute, i.e., vC,  within the capillary; vI, interstitial fluid  space; and vcell, parenchymal cells. At equi-  librium, for a substance passively exchang-  ing between plasma and ISF, vI is the ratio  of the concentration in VI to that in the  plasma and is equal to the partition co-  efficient λ = CI/Cp. For steady-state proc-  esses producing transmembrane fluxes,  the effective volume of distribution is not  the same as the equilibrium ratio, i.e.,  vI ≠ λ
ν F	Velocity of fluid flow, cm·s−1
V’	Volumes of distribution, cm3·g−1. ${\mathrm{V}}_{\mathrm{C}}^{\prime }$, in cap-  illary; ${\mathrm{V}}_{\mathrm{I}}^{\prime }$, in ISF; and ${\mathrm{V}}_{\text{cell}}^{\prime }$, in parenchymal  cell. These are the anatomic volumes times  the fractional volume of distribution, e.g.,  ${\mathrm{V}}_{\mathrm{I}}^{\prime }={\mathrm{v}}_{\mathrm{I}}{\mathrm{V}}_{\mathrm{I}}$. Commonly used ratios are $\gamma ={\mathrm{V}}_{\mathrm{I}}^{\prime }∕{\mathrm{V}}_{\mathrm{c}}^{\prime }$ and $ϴ={\mathrm{V}}_{\text{cell}}^{\prime }∕{\mathrm{V}}_{\mathrm{C}}^{\prime }$
${\tilde{\mathrm{V}}}_i$	Partial molar volume of solute i, cm3/mol; the  increment in the volume of a solution per  mole of added solute, e.g., ${\tilde{\mathrm{V}}}_{\mathrm{w}}\simeq 18{\mathrm{cm}}^3\cdot {\mathrm{mol}}^{-1}$
W	Mass, g (“weight,” mass times gravitational  acceleration)
ω(x)	Weighting function or probability density  function of variable x
ωi or ωi(f)	Weighting or fraction of total in the ith group.  Units are fraction per unit of f. Given a  density function of regional flows, ω(f), in  its finite histogram representation ωiΔfi, is  the fraction of the mass of the organ having  a flow fi, the average of the flows grouped  as the ith class. The fraction of the total  flow going to the regions falling into the ith  class is ωifiΔfi
x	Distance, cm; e.g., distance along the capillary  from inflow, x = 0, to outflow, x = L
$\stackrel{‒}{x}$	Mean of a density function, ω(x); see mean  and moments, α
X	Generalized driving force
xi	Mole fraction of component i; i.e., moles of  the ith component divided by the total moles  in the system, = ni/n, where n is the total
z	Valence of an ionic solute, number of unpaired electrons (or missing electrons) per molecule

Greek symbols

α0, α1, αn	Moments about zero for a probability density  function. (Units are tn when t is the inde-  pendent variable.) [α0 = area; α1 = mean;  for the density function h(t), ${\alpha }_n={\int }_{-0}^{+\infty }{t}^{n}h\left(t\right)\mathrm{d}t$. See central moments, μ
β n–2	Dimensionless parameters of shape of density  function calculated from the central mo-  ments, $={\mu }_n∕{\mathrm{SD}}^n={\mu }_n∕{\mu }_2^{n∕2}$. “β1” is skewness  (or asymmetry); β1 is zero for all symmet-  rical functions, positive for right skewness.  “β2” is kurtosis (or flatness). β2 = 3.0 for  normal density function; β2 > 3 for lepto-  kurtosis (highpeakedness), and <3 for  platykurtosis
γ	Ratio of interstitial volume of distribution  to intracapillary volume of distribution,  ${\mathrm{V}}_{\mathrm{I}}^{\prime }∕{\mathrm{V}}_{\text{cap}}^{\prime }$
Δ	Difference
δ(t)	Unit impulse func-  tion, or Dirac delta function, has unity area, an infinite amplitude  at t = 0, and is zero at all other times. It is  the limit of any symmetrical unimodal den-  sity function of unity area as its width ap-  proaches zero. For delta function occurring  at a nonzero time t0, it is written δ(t – t0)
∊	Epsilon, vanishingly small difference
ζ	Tortuosity of diffusion pathway. ζ is ratio of  apparent path length to measured length of  diffusion pathway, dimensionless; thus the  effective diffusion coefficient, D = D0/ζ2  where D is the free aqueous diffusion coef-  ficient
η	Viscosity, poise (P) = dyn/cm2 = g·s−1·cm−1.  Water viscosity = 0.01002 P at 20°C.  Plasma viscosity ≈ 0.011
η(t)	Equals h(t)/R(t) (fraction/s); the emergence  function, the specific fractional escape rate  following an impulse input. Of the particles  residing in the system for t seconds after  entering, η(t) is the fraction that will depart  or escape in the tth second. In chemical  engineering it is known as the intensity  function (7), and in population statistics as  the risk function, the death rate of those  living at age t. Also, η(t) = (dR/dt)/R(t) =  −d logeR(t)/dt. See FER(t)
Θ	Ratio of intracellular volume of distribution  to intracapillary volume of distribution,  ${\mathrm{V}}_{\text{cell}}^{\prime }∕{\mathrm{V}}_{\text{cap}}^{\prime }$, dimensionless
λ, λij	Partition coefficient, a dimensionless ratio  of Bunsen solubility coefficients in two  phases. λij is the ratio of solubility in region  or solvent i to the solubility in region j. The  reference region j is usually the plasma. At  equilibrium, λij is the ratio of concentra-  tions
μ	Chemical potential for a solute in a solution,  N·m−2; μ = μ0 + RT In a, where the activity  a is a concentration times an activity coef-  ficient and μ0 is the potential at a reference  state of temperature and pressure
μ n	nth central moment of a density function,  h(t), a moment around the mean, $\stackrel{‒}{t}$. ${\mu }_n={\int }_{-\infty }^{\infty }{(t-\stackrel{‒}{t})}^{n}h\left(t\right)\mathrm{d}t$. Units are those of t to  the nth power
μ2, μ3, μ4	μ2 is variance, the second moment of a density  function around the mean, $={\alpha }_2-{\alpha }_1^2$. Also  ${\mu }_3={\alpha }_3-3{\alpha }_1{\alpha }_2+2{\alpha }_1^3$ and ${\mu }_4={\alpha }_4-4{\alpha }_1{\alpha }_3+6{\alpha }_1^2{\alpha }_2$. See also βn
π	Osmotic pressure, Pa or N·m−2 or mmHg, is  the pressure that would have to be exerted  on a solution to prevent pure water from  entering it from across an ideal semiperme-  able membrane, i.e., a membrane permeable  to solvent only. π = CRT is Van’t Hoff’s  law for ideal dilute solutions, and across a  membrane impermeable to solute. π =  φCRT is preferred to account for activity  coefficients less than unity. When the sol-  ute can permeate the membrane, the effec-  tive π = σφCRT. Osmotic pressure, a colli-  gative property of solutions, is related to  actual pressure rn the same fashion as a  freezing point is to actual temperature. On-  cotic pressure is a term, now obsolete al-  though historically useful, for the osmotic  pressure associated with the presence of  large, relatively impermeant molecules such  as plasma proteins. It should now be re-  placed by more exact terms, e.g., across  some specific membrane the effective Δπ  equals $RT{\phi }_{i=1}^{i=N}{\sigma }_i{\varphi }_i\Delta {\mathrm{C}}_i$, where the effects of  concentration differences for a set of N  solutes are summed.
ρ	Density, g·cmm−3. (Specific gravity is density  relative to density of water)
σ	Reflection coefficient, in notation of irrevers-  ible thermodynamics, dimensionless; σ =  –LpD/Lp or, experimentally, σ = –JD/Jv for  ΔC8 = 0. The effective osmotic pressure  across a membrane is σΔπ, mmHg; i.e., σ =  (observed osmotic pressure)/CRT
τC	Capillary mean transit time, t̄c, used in Krogh  cylinder capillary-tissue models with plug  flow velocity profiles
φ	Activity coefficient, the ratio of apparent  chemically effective concentration to the  actual concentration in a solution, in the  absence of chemical binding, dimensionless.  The osmotic activity coefficient φ = π/CRT
ψ	Electrical potential, V
ω	Solute permeability coefficient, ω = P/RT,  mol·cm−2. s−1 ·(mmHg)−1. In the notation of  irreversible thermodynamics ω = (LD – RT/F  σ2Lp)C̄s, where C̄s, is the average solute con-  centration across the membrane

Physical Units, Constants

A	Ampere, unit of electrical current, coulomb  per second (C·s−1)
Å	Ångstrom, 10−10 m or 0.l nm
C	Charge, coulomb, ampere· second (A. s)
°K	Degrees of temperature, Kelvin (absolute); °C  for degrees Celsius = 273.15 + °K
dyn	Dyne, force, g·cm·s−2 = 10−5 N (newton)
eq	Equivalent weight = molecular weight/va-  lence. One equivalent carries 9.65 × 104 C  of charge
e	Elementary charge, 1.6021892 × 10−19 C
erg	Energy, dyn·cm = g·cm2·s−2 = 10−7 J
F	Faraday constant, 9.648456 × 104 elementary  charge. eq−1 = 96,484.6 C· mol−1 = NAe
g	Acceleration due to gravity = 980.665 cm·s−2
h	Planck’s constant (energy quantum) =  6.626176 × 10−27 erg·s = 6.626 × 10−34 J·s
η	Viscosity; 1 poise (P) = 1 cm−1· g·s−1 = 0.1  Pascal·second (Pa·s)
I	Current, amperes
J	Joule = Watt·second (W ·s) = ampere·volt·  second (A·V·s) = 107 erg = 107 cm2g·s−2
k	Boltzmann constant, 1.380662 × 10−23 J. °K−1  = R/NA, the gas constant over Avogadro’s  number = 1.37900 × 10−16 cm2·g·s−2·°K−1
1, liter	Liter = 1 dm3 = 1,000 cm3. Also milliliter (ml)  and microliter (μl)
M	Mol/l (molarity)
mol/kg	Mol solute/kg solvent (molality)
N	Newton = 105 dyn = 105 cm·g·s−2
N A	Avogadro’s number, 6.022045 × 1023 mol−1,  the number of molecules contained in 1 mol
ns, nw	Number of moles of solute and water
P	Pressure (= force per unit area), N·m−2 or Pa  (Pascal). (1 Pa ≡ 1 N·m−2 ≡ 10 g·cm−1·s−2  ≡ 10−2 mbar ≡ 0.10197 mmH20 ≡ 7.5 ×  10−3 mmHg ≡ 9.869 × 10−6 atm; or 1 atm =  101325 Pa = 760 Torr; 1 cmH20 (at density  1 g·cm−3) = 98.0665 Pa = 981 g·cm−1·s−2;  1 mmHg = 1.00000014 Torr = 133.322 Pa  = 1,333 g·cm−1 · s−2
ρ	Density, g·cm−3. Water (3.98°C, 1 atm) =  0.999972 g·cm−3. Mercury (0°C, 1 atm) =  13.59508 g·c−3
R	Resistance, electrical (Ω), or electrophysiolog-  ical (Ω/cm2) or vascular (a pressure divided  by a flow)
R	Universal gas constant = 8.31441 J.mol−1  °K−1 = 8.3144 × 107 cm2 ·g·s−2 ·mol−1 °K−1  = 0.082 1· atm· mol−1 °K−1 = 0.0623 mmHg·  mmol−1· °K−1 = 8.31441 × 10−7 erg·mol−1·  °K−1
RT	Energy/mol, gas constant × absolute temper-  ature; e.g., at 37°C or 310.16°K, RT = 19.34  × 106 mmHg· cm3· mol−1
RT/F	24.84 mV at 15°C.26.62 mV at 37°C. Values  of loge,10 RT/F at 15, 20, 25, 30, and 37°C  are 57.2, 58.2, 59.2, 60.2, and 61.3 mV
STP	Standard temperature and pressure (ice point  of water, 0°C = 273.16°K; 760 mmHg = 1  atm = 1.01325 × 106 dyn·cm−2 = 1.013 ×  105 N· m−2)
T	Temperature, absolute, in degrees Kelvin  (°K); 0°C = 273.16 °K
V	Volts; millivolt, mV; microvolt, μV
Ṽ i	Partial molar volume, ml/m01 =  (∂V/∂ni)T,p,njj≠i = change of volume of total  system per mole additional solute i, at T, p,  and constant presence of other components  j, and at the particular concentration ni/V.  (ṼW is the partial molar volume of water;  close to 18 ml/mol for physiological solu-  tions)
Watt	Unit of power, joules per second, J·s−1
Work	Work is energy × time or force × distance ×  time, erg·s or J· s or cm2g·s−1
Ω	Ohm, unit of electrical resistance; V/I