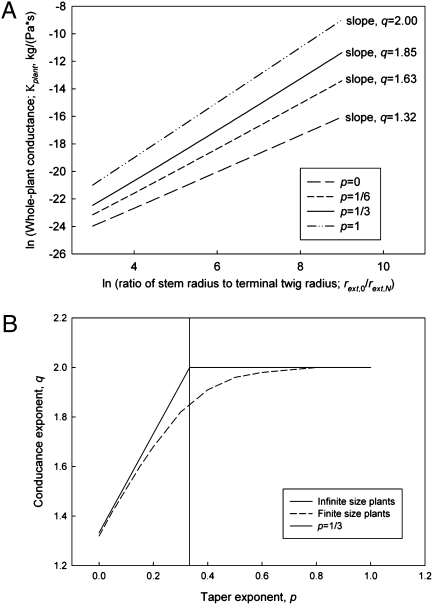
Fig. 2.

(A) Plots of the logarithm of conductance [kg/(Pa·s)] vs. the logarithm of the ratio of base radius to terminal twig radius. We chose taper exponents of p = 0, 1/6 (WBE model), 1/3 (our model), and 1. We used n_ext = 2, r_ext,N = 0.5 mm, l_ext,N = 5 mm, μ = 10⁻⁶ kg/(mm·s), ρ = 1 g/cm³, r_int,N = 0.01 mm, 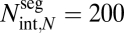, and a size range of r_ext,0 = 1 cm to r_ext,0 = 4 m for our parameters. The corresponding effective conductance exponent, q, is given beside each line. (B) Plot of the conductance exponent, q, vs. the taper exponent p. For plants of infinite size, the asymptotic relation is q = 4/3 + 2p for p ≤ 1/3 and q = 2 for p ≥ 1/3. For a realistic size range of r_ext,0 = 1 cm to r_ext,0 = 4 m (finite-size plants), q varies continuously with p. Nevertheless, the point of maximum curvature (i.e., the magnitude of the second derivative) occurs at p = 1/3, seemingly always an important transition point in the scaling of whole-plant conductance.