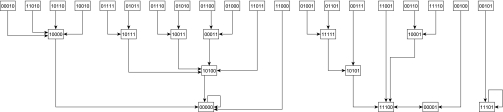
Fig. 2.

The state transition network that corresponds to the interaction network shown in Fig. 1. Dynamically, the presence or absence of a species at time 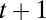is determined by the species that target it and are present at time t. Here, the effect of a negative edge is equal to that of a positive edge, and a species must have more active positive incoming edges than negative at time t to be present at time t + 1 (Materials and Methods). The 32 possible community states are identified with a binary number (present = 1, absent = 0) where the values correspond to (from left to right) plant 1, 2, 3 and pollinator 1, 2. Edges indicate the succession of the system's states in the absence of outside influence. The system admits two steady states, 00000 (presence of no species) and 11101 (absence only of pollinator 1), and one cycle of length 2, 11100 ↔ 00001 (the system oscillates between all plants and no pollinators and only pollinator 2). Note that due to the artificial nature of this example interaction network, this limit cycle is highly unrealistic, and such limit cycles are extremely uncommon in larger, more realistic interaction networks.