Fig. 1.

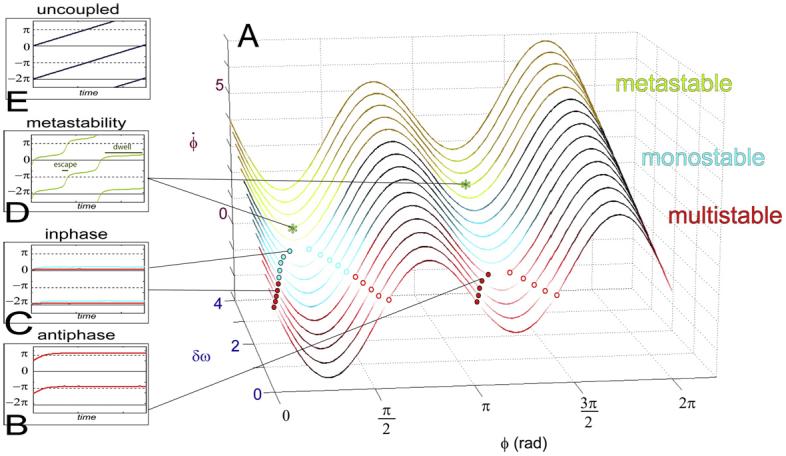
A simple theoretical model of brain coordination dynamics exhibits multistability, adaptive phase shifts, critical phase transitions and metastability. Each source element is capable of intrinsic oscillation. The key collective variable that characterizes the coordination between source elements is the relative phase. (A) Shows the flows of the relative phase (ϕ) for varying parameter values of δω (difference between each element's intrinsic oscillatory frequency) and for fixed coupling values. Boxes show the corresponding phase behavior as a function of time. Flow lines passing through $\stackrel{.}{\varphi }=0$ define the fixed points of the coordination dynamics (places where the rate of change of the relative phase is null). Stable fixed points (attractors) are shown as filled circles; unstable fixed points (repellers) as open circles. Red flow lines are multistable: depending on initial conditions, trajectories of the relative phase are attracted near antiphase (B) or inphase (C, red). When the pair of fixed points near antiphase collides and disappears, a bifurcation occurs to the monostable regime in which the relative phase is exclusively attracted near inphase (C, blue). Green flow lines (A) belong to the metastable regime. All the fixed points have disappeared and only “remnants” remain. Coordinative tendencies emerge with successive dwellings near inphase and antiphase (D). For reference, relative phase of uncoupled sources is shown in (E). One can readily see that metastability (A) lies between fully coupled, integrated states (C, D) and totally uncoupled, segregated states (E).