Hopping around an entropic barrier created by force

Abstract

We use Langevin dynamics to investigate the role played by the recently discovered force-induced entropic energy barrier on the two-state hopping phenomena that has been observed in single RNA, DNA and protein molecules placed under a stretching force. Simple considerations about the free energy of a molecule readily show that the application of force introduces an entropic barrier separating the collapsed state of the molecule, from a force-driven extended conformation. A notable characteristic of the force induced barrier is its long distances to transition state, up to tens of nanometers, which renders the kinetics of crossing this barrier highly sensitive to an applied force. Langevin dynamics across such force induced barriers readily demonstrates the hopping behavior observed for a variety of single molecules placed under force. Such hopping is frequently interpreted as a manifestation of two-state folding/unfolding reactions observed in bulk experiments. However, given that such barriers do not exist at zero force these reactions do not take place at all in bulk.

Introduction

In 1978 George Bell proposed what became the paradigm for the effect of force on the energy landscape of a molecule [1]. In his view, a force perturbation, F, linearly tilts the two-state free energy of a molecule along the pulling coordinate x, by an amount F·x. While it was originally intended to describe bond rupture events over short length scales, this model has been adopted to analyze force-spectroscopy measurements on single RNA, DNA and protein molecules that extend by up to tens of nanometers [2; 3; 4]. Liphardt et al. were the first to report that a simple RNA hairpin would hop under force between folded and unfolded states separated by distances of up to 26 nanometers [2]. These observations were followed by a series of experiments probing the energy landscape of a wide range of RNA and DNA hairpins [4; 5]. Similar two-state hopping behavior under force was also observed in proteins as varied as RNAse H [3] calmodulin [6], ankyrin and β-catenin [7]. In all these cases a signature feature of the hopping experiments were the long distances to transition state that made the observed kinetics highly force dependent where a 1-2 pN change was enough to tilt the probability of unfolding from 0 to 1 [2; 3; 4; 5]. Remarkably, good agreement was found between the values of ΔG obtained by extrapolating the rates of hopping to zero force and those of untethered molecules [2; 3; 4; 5]. Thus, the hopping kinetics could be readily compared with that observed in bulk, suggesting that both types of experiments sampled the same energy barriers (Figure 1A). However, is it physically possible for an untethered molecule to have a thermodynamically stable state that is tens of nanometers away from its native folded state? This proposition contradicts over a century of studies of polymer physics showing that free polymers collapse readily, and that the entropic costs of extending them is very high [8]. Here we use Langevin dynamics to probe the behavior of a single protein while it hops around the force-induced entropic barrier under constant velocity conditions. Such hopping transitions have been frequently misinterpreted as a signature of two-state folding/unfolding reactions. Here, for the first time, we clarify their origin.

Figure 1.

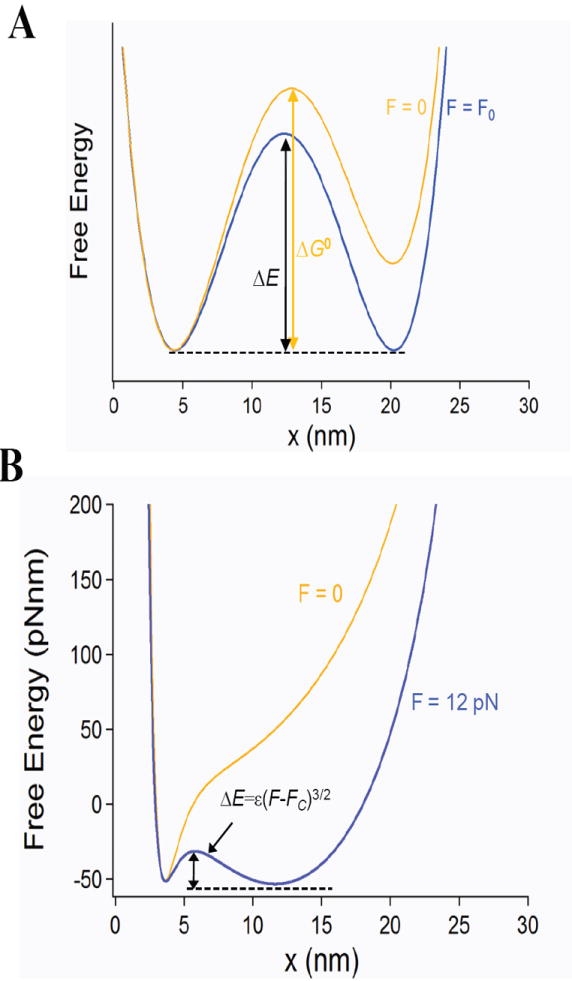
The free energy landscape of a molecule under force. A) Typical energy landscape representation commonly used to interpret force spectroscopy data, showing a putative thermodynamic state that is tens of nanometers away from its native folded state that is apparent both under general force F₀ and also in the absence of force. B) Free energy representation of an extending molecule that can be simply modeled as the sum of an entropic term (WLC) and an enthalpic term accounting for the short range interactions that define the collapsed protein. The free energy of a simple molecule in bulk (F=0) contrasts with the same molecule under a force of F=12 pN. The energy cost of extending is calculated from the WLC model of polymer elasticity (L_c=30 nm, p =0.4 nm), the drive to collapse is represented by a Morse potential (U_min= 60 pNnm, x₀=4 nm). Notice the absence of a stable extended state for F=0. Under a constant stretching force of 12 pN a new entropic energy barrier appears separating the entropic minima at 15 nm, from the collapsed minima at 4 nm. This barrier is completely absent below the critical force F_c.

Materials and Methods

Langevin dynamics

Our Langevin simulations followed the procedures described in Berkovich et al. [9], but modified for constant velocity, ν, conditions. Our system is composed of a stiff linker in series with the molecule and in series with the probe. All three systems equilibrate at the same force. The linker is a random coil described by its contour length and persistence length, L_l = 150 nm and P_l = 10 nm respectively. The molecule is the one represented by the free energy shown in Figure 1 B. The molecule is described by L_m = 30 nm and P_m = 0.4 nm together with an attractive enthalpic potential (Morse) with the parameters U₀ = 60 pNnm, a collapsed minimum of R_c = 4 nm and b = 2. The probe is treated as a simple harmonic potential with a spring constant k_s that varies depending on the type of experiment being simulated. The force applied depends on the displacement of the probe, x₃, with respect to its vertex (x₀). In all cases, while the type of linker and spring constant of the probe varies, the molecule is the same throughout.

The dynamics of the end-to-end length of the linker, x₁, is described by

$$\frac{{\mathit{dx}}_1}{\mathit{dt}}=\frac{1}{\varsigma }(f_1+\mathrm{\Gamma }(t)+k_S{x}_3)$$ (1)

where

$$f_l={\frac{{\mathit{dU}}_l}{\mathit{dx}}\mid }_{x_1}{=\frac{k_{B}T}{P_l}[\frac{1}{4}{(1-\frac{x}{L_l})}^{-2}-\frac{1}{4}+\frac{x}{L_l}]\mid }_{x_1}$$ (2)

Here ς = k_BT/D is the friction coefficient where k_B is Boltzmann’s constant, T is the absolute temperature and D=1500 nm²/s is the self-diffusion coefficient Γ(t) is the fluctuating random force which is a white noise with a Gaussian distribution defined by 〈Γ(t)〉 = 0 and 〈Γ(t)Γ(t’)〉 = 2ςk_BTδ(t−t’). The brackets <…> denote a statistical average over an ensemble of particles and δ(t) is the Dirac delta function.

The dynamics of the end-to-end length of the molecule, x₂, is described by

$$\frac{{\mathit{dx}}_2}{\mathit{dt}}=\frac{1}{\varsigma }(f_m+\mathrm{\Gamma }(t)+k_S{x}_3)$$ (3)

where

$$f_m={\frac{{\mathit{dU}}_m}{\mathit{dx}}\mid }_{x_2}={-3U_0\frac{b}{R_C}{e}^{-2\frac{b}{R_C}(x-R_C)}\left(1-e^{-2\frac{b}{R_C}(x-R_C)}\right)\mid }_{x_2}+{\frac{k_{B}T}{P_m}\left[\frac{1}{4}{\left(1-\frac{x}{L_m}\right)}^{-2}-\frac{1}{4}+\frac{x}{L_m}\right]\mid }_{x_2}$$ (4)

The constant velocity condition is defined by;

$$x_1+x_2+x_3=\mathit{vt}$$ (5)

Iteratively solving equations 1 to 5 produces the time evolution of x₁, x₂ and x₃, from which we obtain all the behaviors described in this paper.

Simulations under conditions similar to those employed in Optical Tweezers and AFM experiment

Figure SI 1 in the supporting material shows force and extension traces of a simulation where the molecule is attached to a long rigid linker (P_l = 10 nm and L_l = 150 nm) and extended at constant velocity (ν = 50 nm/s) with a soft cantilever (k_S = 0.05 pN/nm). These parameters were chosen to simulate the conditions that are common to optical tweezers experiments [2]. In these simulations, the molecule was extended until the restoring force reached a certain predefined value (11.4 pN in the figure) after which the total length (x₁ + x₂ + x₃) was held constant by setting ν = 0. Hopping is observed in both the force measured as well as in the end-to-end length of the molecule (x₂). Under these conditions the hops in force are small (<0.5 pN) while the hops in length are large (>10nm). In these experiments F_1/2 defines the force at which the molecule spends equal time in the extended and collapsed state.

Simulations under conditions similar to AFM (Figure SI 2) were performed with a stiffer probe (6 pN/nm), a shorter but softer linker (Lc_l =5 nm and P_l = 0.4 nm) and very low pulling speeds (1 nm/s) in order to approximate the conditions used in the AFM experiments of Junker et al. [6].

Results

As we recently showed [9], the free energy of an extending molecule can be simply modeled as the sum of an entropic term described by the Worm like Chain model (WLC) of polymer elasticity, plus an attractive enthalpic term accounting for the short range interactions that cause a molecule to collapse. In Figure 1 B we follow the design of Berkovich et al. [9] to calculate the free energy of a generic molecule with a contour length of 30 nm and a collapsed length of 4 nm. This simplified polymer model applies to any untethered molecule in solution. This model is restricted to the collapse behavior of a molecule and does not include the internal barriers that define the final folding transition. As the free energy profile shows (Figure 1 B), in the absence of a perturbation, molecules cannot stably extend by tens of nanometers, as it would be inferred from the energy landscape shown in Figure 1 A, which is typically used to interpret single molecule folding data [3; 4]. Two recent papers [9; 10] have shown that under force-clamp conditions, a new energy barrier forms between a force-dependent entropic minimum and the enthalpic minimum of the collapsed molecule (ΔE, Figure 1 B). The entropic minimum marks the average end-to-end length of a molecule at a given force F. It was shown that the magnitude of this new barrier was very sensitive to the stretching force following ΔE=ɛ(F-F_c)2/3 where F_c is the critical force below which the barrier disappears [9]. Figure 1 B shows the free energy barrier (ΔE) that results from applying 12 pN to the generic untethered molecule (F=0). Key features of this newly discovered barrier are the very long distances between minima as well as to the respective transition states.

The entropic barrier that forms when force is applied to a molecule is not unique to force-clamp conditions. Under constant velocity conditions, perturbation of the molecule by the harmonic potential of the probe creates a similar entropic barrier that changes as the probe is moved. Here we use Langevin dynamics to examine the behavior of a molecule while it hops around the entropic barrier that forms under constant velocity conditions. In our simulations (see Materials and Methods section) we use conditions that approach those used in optical tweezers studies including a soft probe (k_s=0.05 pN/nm) and long stiff linkers (L_contour=150 nm) [11]. Figure 2 A shows that as the molecule is extended at a constant velocity of 10 nm/s the force rises until a peak value followed by a two state hop between the enthalpic and entropic minima, settling in the “unfolded’ state as the protein is extended further. Upon retraction, the molecule collapses back through the same path and at some force it jumps back to the “folded” state. If the pulling speed is increased (100 nm/s, 500 nm/s) the hops disappear and the “unfolding” and “folding“ forces become more widely separated as the molecule moves further away from equilibrium [2]. If the extension is arrested and held constant just before the force peak, a remarkable series of hops both in force and length are observed (Figure SI 1), mimicking those observed experimentally [2; 3; 4; 5; 6]. For softer springs (e.g. k_s=0.05 pN/nm), the magnitude of the force hops is small and the hops in length are large (Figure 2 B), approaching constant force conditions. The same molecule probed with stiffer springs (e.g. k_s=6 pN/nm) produces the opposite, where the hops in force are largest and the hops in length are small in amplitude (Figure SI 2). Slight adjustments in the extension at which the molecule was held resulted in different forces which rapidly tilt the hopping probability upwards or downwards (Figure 2 B).

Figure 2.

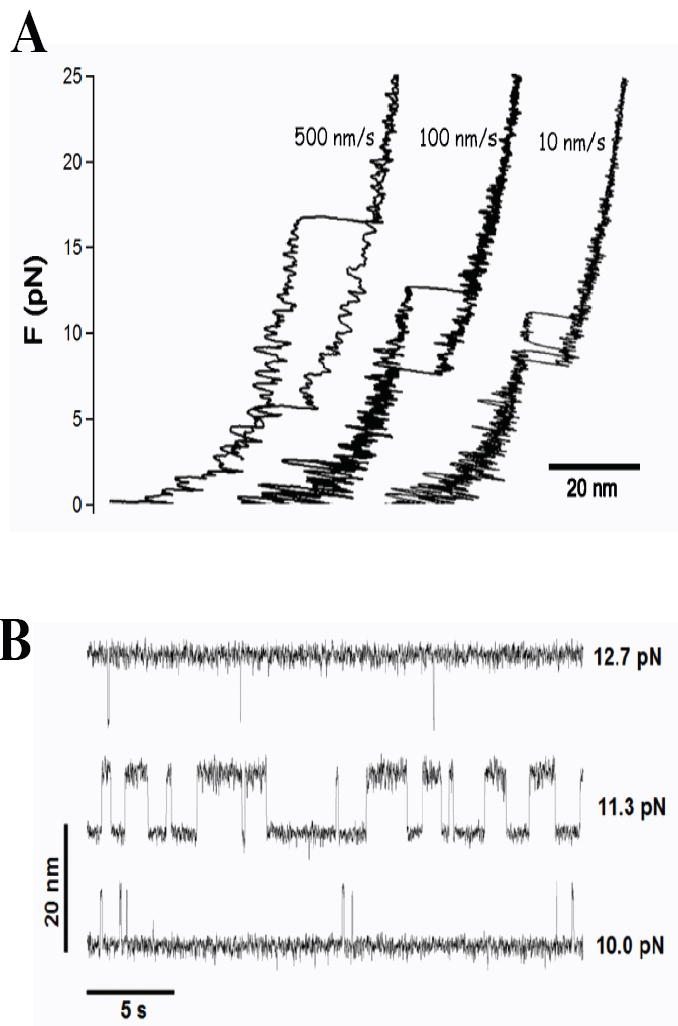
Langevin dynamics demonstrating the behavior of a molecule as it crosses the entropic barrier created by the pulling probe. The simulation shows “unfolding” and “refolding” events and hopping across the entropic barrier. The perturbing probe has a spring constant of k_s=0.05 pN/nm and a stiff DNA-like linker (L_c=150 nm, p =10 nm) was added to approximate the experimental conditions used in optical tweezers experiments. A) Force-extension experiments at constant velocity; ν =500, 100 and 10 nm/s. B) By arresting the extension at different points it is possible to observe hops in length at different forces.

The measured hopping frequency (dwell times) and force dependency are highly sensitive to linker lengths and stiffness of the pulling device as you expect from the touchy tuning of an oscillator. In this sense, the observed hopping kinetics can be considered to be an artifact. Thus, paradoxically, two investigators probing the same molecule using force probes with different spring constants may measure very different kinetics and free energy profiles from their experiments (Figure 3 and [12]). Indeed, under constant velocity conditions the curvature of the probe potential (e.g. stiffness of the pulling spring) has a large effect on the entropic barrier that forms (Figure 4). Passive-force clamp [13] or the slow active feedback common to optical tweezers experiments [11] will also distort the perturbing potential with unknown effects on the entropic energy barrier described here. Given that the entropic barrier is largest under true force-clamp conditions (Figure 4), it may be the case that an investigator using a stiff force probe (e.g. 6 pN/nm) will observe rapid hopping of a molecule across a much reduced entropic barrier. Such hopping would drastically slow down or altogether disappear when switching to the force clamp mode, due to the much larger entropic barrier that forms (Figure 4). However, if softer probes are used (e.g. 0.1 pN/nm), there will not be much difference between force-clamp and constant velocity conditions [14].

Figure 3.

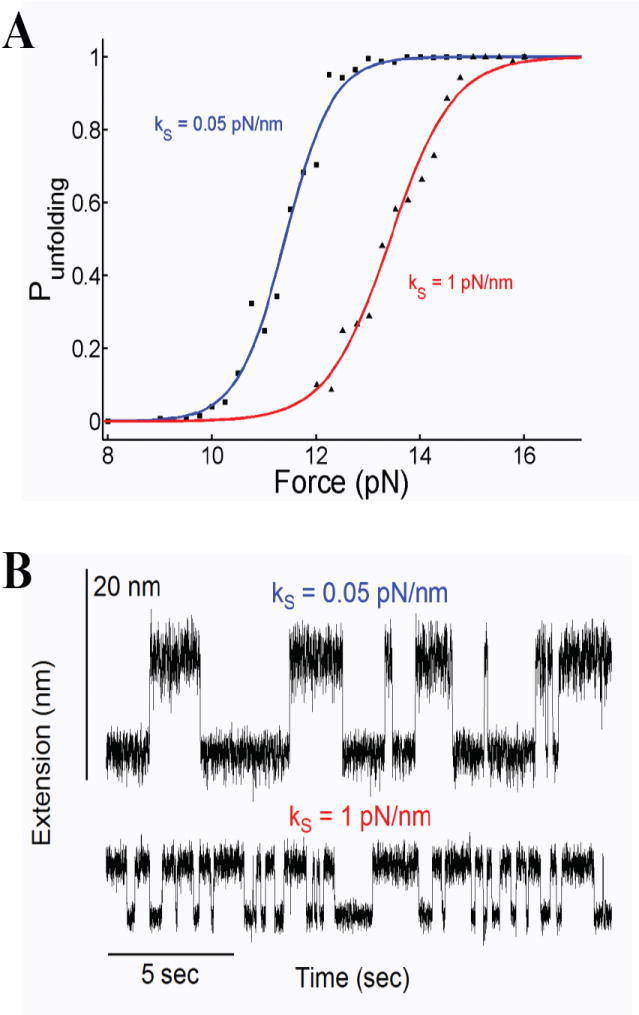
Effect of the spring constant on the hopping dynamics. A) Probability of unfolding as a function of force. The data was obtained for two different spring constants showing the large effects that the experimental conditions have on the hopping kinetics and the reconstructed free energy barrier. The data shows a steep dependency on force which is well describe by a sigmoid. We analyze these data using the form $P(F)={(1+\exp [-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathit{kT}$}\right.(F-F_{1/2})\mathrm{\Delta }x\left]\right)}^{-1}$ as used by Liphardt et al. [2]. Fits of P(F) to the data obtained with k_s = 0.05 pN/nm measured values of F_1/2 = 11.4 pN, ΔG = 103 pN nm and Δx = 9.06 nm. Remarkably, the same experiments repeated with k_s = 1 pN/nm now measure different values with F_1/2 = 13.4 pN, ΔG = 92 pN nm and Δx = 6.83 nm for the same molecule. B) The corresponding end-to end distances at F_1/2 for the two cases showed in A).

Figure 4.

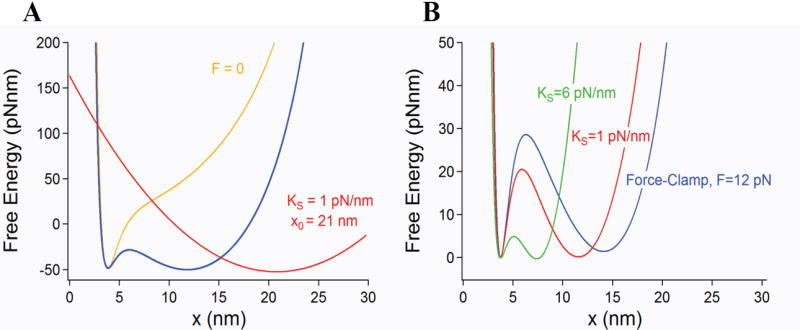
Free energy of a single molecule perturbed by an harmonic potential. This is the most typical experimental configuration both for optical tweezers and AFM experiments. A) A force probe modeled as a harmonic potential (red trace) is moved along the pulling coordinate x at a velocity ν. The harmonic potential of the probe deforms the free energy of the relaxed molecule (yellow trace) creating an entropic barrier (blue trace) that is similar but smaller than that obtained under constant force conditions. B) The magnitude of the resulting barrier is dependent on the curvature of the potential (spring constant) of the pulling probe. The figure shows barriers calculated for k_s=1 (red) and 6 (green) pN/nm which are always smaller and shorter than that obtained under force–clamp conditions. The barriers are compared under conditions where the entropic and enthalpic minima have approximately the same energy at F_1/2. As the spring constant of the probe is increased, the magnitude of the entropic barrier decreases and the distance between the entropic and enthalpic minima also becomes shorter. This is caused by the changing curvature of the perturbing potential which has a large influence on the shape and size of the resulting entropic barrier. The largest barrier is encountered under force-clamp conditions where it becomes independent of the linkers and spring constant of the probe.

Discussion

The force/length hops that we observe in our simulations (Figure 2) undoubtedly result from thermally driven transitions across the entropic barrier created by pulling a molecule with a spring. It is interesting to consider here that the continuous collapse plateau observed in force-quench experiments [9; 15; 16], and the two state hopping observed in constant velocity experiments [2; 3; 4; 5; 6; 7] are both manifestations of the same entropic barrier. Indeed, the long distances to transition state and overall elongation of the molecules measured in those hopping experiments is readily explained now by the appearance of the entropic barrier. More importantly, the barrier around which the hopping occurs vanishes completely at zero force and therefore these reactions do not take place at all in bulk experiments where molecules are free in solution [9; 10]. Hence, any estimate of ΔG values from hopping across such entropic barrier will not be relevant to bulk equilibrium. Owing to its long distances, the entropic barrier created by pulling manifests itself at low forces in the 5-20 pN range depending on the experimental conditions (Figure 2). Thus, hopping observed in this range of forces might be caused by such a barrier. Therefore, extra testing would be needed to determine if the measured barrier is purely entropic, as shown here.

So far we have shown that the simple collapse behavior of a molecule under force can be easily confused with the folding/unfolding reactions measured in bulk (Figure 2). Then, how do we reconcile these observations with those made in bulk? A more complete representation of the free energy of a protein along the pulling coordinate x requires the addition of an inner barrier representing the native and unfolded states of a protein, as shown in Figure SI 3. The figure shows a first barrier between the native state (N) and an unfolded molten globule state (MG), which is very close in distance to the native state [17]. Of most interest is to study these inner barriers which are molecule/structure specific and occur over short distances. These short-length inner barriers are the ones typically probed by force spectroscopy at high forces [18], FRET [19] and SAXS[20].

Force spectroscopy extends the range of end-to-end distances over which molecules are probed, but also introduces a new entropic energy barrier which is distinct from those probed in bulk and that vanishes at zero force. Such barrier, encountered in the low force regime, is therefore a generic property of all tethered molecules placed under force. However, the role played by this barrier in-vivo, if any, remains to be determined.