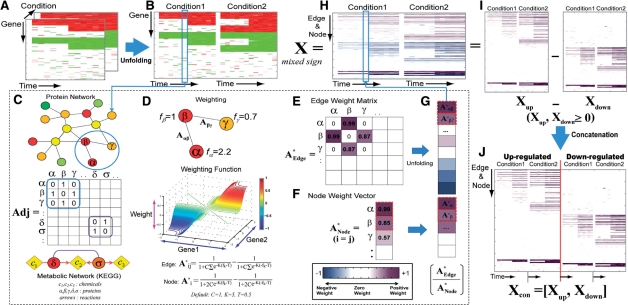
Fig. 1.

Construction of an activation weight matrix. PNA first transforms multi-dimensional expression data into log2-fold changes (A) and unfolds it into a two-dimensional matrix (B). We then represent the edges with the adjacency matrix Adj (C). Using a weighting function (D), the PNA then computes both edge (A^*_Edge) and node (A^*_Node) activity weights (E and F), unfolds the A^*_Edge into a vector and concatenates it with A^*_Node, resulting in a weight vector for each condition (G and H). For the ONMF analysis, we represented the activity weight matrix (X) with X = X_up−X_down (I) and then concatenated X_up and X_down to result in X_con = [X_up, X_down] (J).