Abstract
1:1 Equilibrium constants, K, for the association of hydrogen bond bases and hydrogen bond acids have been determined using solvent octan-1-ol at 298 K for 30 acid-base combinations. The values of K are much smaller than those found for aprotic, rather non-polar solvents. It is shown that the log K values can satisfactorily be correlated against αH2*βH2, where αH2 and βH2 are the 1:1 hydrogen bond acidities and basicities of solutes. The slope of the plot, 2.938, is much smaller than those for log K values in the non-polar organic solvents previously studied. An analysis of literature data on 1:1 hydrogen bonding in water yields a negative slope for a plot of log K against αH2*βH2, thus showing how the use of very strong hydrogen bond acids and bases does not lead to larger values of log K for 1:1 hydrogen bonding in water. It is suggested that for simple 1:1 association between mono-functional solutes in water, log K cannot be larger than about −0.1 log units. Descriptors have been obtained for the complex between 2,2,2-trifluoroethanol and propanone, and used to analyze solvent effects on the two reactants, the complex, and the complexation constant.
Introduction
A direct measure of hydrogen bonding between a hydrogen bond acid, A-H, and a hydrogen bond base, :B, is the equilibrium constant, K, for eq 1 in a specified solvent. The acid and the base are normally present at low concentration to avoid any self-association. In this work, we shall use molar concentrations so that the units of K are dm3mol−1; the temperature is always 298 K
| (1) |
Joesten and Schaad 1 carried out a very valuable survey of equilibrium constants for over 150 acids against a very large number of bases, mostly reported using tetrachloromethane as the solvent, and Green 2 surveyed equilibrium constants for C-H acids against a variety of bases, again mostly with solvent tetrachloromethane. In spite of this wealth of information, little was done to codify the data. Abboud and Bellon 3 had pointed out that under some circumstances it would be possible to use log K values for a series of bases against several reference acids to establish a general scale of hydrogen bond basicity, but it was not until 18 years later that general scales of hydrogen bond acidity and hydrogen bond basicity were established, as follows.
If values of log K are determined for a series of hydrogen bond acids against a standard base in, say, tetrachloromethane, the series of log K values represents the relative hydrogen bond acidity of the series of acids. Abraham et al. 4, 5 showed that when 45 such series of log K values were plotted against each other, they formed 45 straight lines that intersected at a point where all the log K values = −1.1 (with the K-values of the molar scale). This enabled a general hydrogen bond acidity scale, KHA, to be defined through eq 2, where LB and DB are coefficients that refer to a given base. The log KHA values were then converted into a more practical scale through eq 3; addition of 1.1 ensures that the origin of the scale is now at zero instead of −1.1, and the factor 4.636 simply gives a convenient spread of values. Eq 3 represents the definition of the term αH2 which now forms a scale of solute hydrogen bonding in 1:1 complexes.
| (2) |
| (3) |
In exactly the same way, 6, 7 when various series of log K values for hydrogen bond acids against 34 hydrogen bond bases were plotted against each other, all the lines intersected again at −1.1, and a general scale of solute 1:1 hydrogen bond basicity was defined through eqs 4 and 5.
| (4) |
| (5) |
Finally, the entire series of 1312 equilibrium constants used to construct eqs 2–5 could be used to obtain an equation, eq 6, from which it was possible to predict thousands of log K values in tetrachloromethane at 298 K for various combinations of hydrogen bond acids and hydrogen bond bases. 8
| (6) |
In eq 6, N is the number of data points, R is the correlation coefficient and SD is the standard deviation. Some time later, Raevsky et al. 9 devised an equivalent scale, but in terms of Gibbs energies rather than log K values.
Marco et al. 10 have obtained an equation of the general type of eq 6, that is eq 7, for 1:1 complexation in the gas phase, an equation is known for complexation in 1,1,1-trichloroethane, 11 and Abraham and Berthelot 12 have used literature data to obtain coefficients in eq 7 for the solvents carbon disulfide, cyclohexane and 1,2-dichloroethane and we have obtained coefficients for a number of solvents for which equilibrium constants were available as follows: perfluorohexane, 13 hexane or heptane, 1, 14–18 benzene, 1, 14–22 benzonitrile, 23 chlorobenzene, 1, 24, 25 bromobenzene, 1, 26 and an updated equation for 1,1,1-trichloroethane. 11, 27 The coefficients in eq 7 are given in Table 1.
TABLE 1.
| Solvent | c | m | N | R2 | SD | Ref |
|---|---|---|---|---|---|---|
| gas phase | −0.870 | 9.130 | 23 | 0.974 | 0.200 | 10 |
| perfluorohexane | −1.100 | 8.560 | 14 | 0.288 | This work | |
| hexane/heptane | −1.252 | 7.967 | 65 | 0.878 | 0.337 | This work |
| carbon disulfide | −1.120 | 8.010 | 12 | 0.982 | 0.130 | 12 |
| cyclohexane | −0.954 | 7.674 | 430 | 0.975 | 0.174 | 12 |
| tetrachloromethane | −1.094 | 7.354 | 1312 | 0.991 | 0.093 | 8 |
| tetrachloroethene | −1.087 | 7.382 | 79 | 0.993 | 0.107 | This work |
| o-dichlorobenzene | −1.215 | 7.204 | 32 | 0.962 | 0.171 | This work |
| 1,1,1-trichloroethane | −1.098 | 6.763 | 94 | 0.957 | 0.164 | This work |
| chlorobenzene | −1.110 | 6.860 | 14 | 0.971 | 0.145 | This work |
| bromobenzene | −1.100 | 6.730 | 6 | 0.098 | This work | |
| 1,2-dichloroethane | −1.270 | 6.260 | 70 | 0.940 | 0.140 | 12 |
| dichloromethane | −1.364 | 6.288 | 97 | 0.895 | 0.251 | This work |
| benzene | −0.582 | 5.624 | 83 | 0.905 | 0.226 | This work |
| chloroform | −1.100 | 4.697 | 27 | 0.374 | This work | |
| benzonitrile | −1.100 | 4.48 | 14 | 0.171 | This work | |
| octan-1-ol | −0.710 | 2.860 | 27 | 0.948 | 0.103 | This work |
Where c is fixed at −1.10, no value of R2 can be given.
| (7) |
These solvents, such as dichloromethane, trichloromethane, tetrachloroethene and benzene are all rather non-polar. Cook et al. 28 have recently obtained values of the 1:1 equilibrium constant for hydrogen bonding between the strong hydrogen bond acid, perfluoro-tert-butanol, and the strong hydrogen bond base, tri-n-butylphosphine oxide, in a variety of solvents including polar solvents such as dimethylsulfoxide and decan-1-ol. Values of K decrease very considerably from 105 in cyclohexane to 0.68 in DMSO and to 0.16 in decan-1-ol. Of course, it is impossible to obtain the coefficients in eq 7 with data on only one acid-base pair, but the results show that hydrogen bonding becomes increasingly unfavorable as the solvent becomes more polar.
Hunter 29 devised an extension of eq 7 to enable values of K to be predicted in solvents other than tetrachloromethane,
| (8) |
In eq 8, α = 4.1(αH2 + 0.33) and β = 10.3(βH2 + 0.06). The parameters αs and βs that characterize the solvent are actually solute parameters derived from αH2 and βH2 through the previous expressions. Equation 8 predicted values of log K for the perfluoro-tert-butanol/tri-n-butylphosphine oxide pair in non-polar and polar solvents in good agreement with experiment, except for the only hydroxylic solvent used, that was decan-1-ol.
We wished to determine 1:1 equilibrium constants for a variety of acid-base systems in an hydroxylic solvent to see if eq 7 still holds, and also to shed some light on hydrogen bonding in water. We selected (dry) octan-1-ol as a hydroxylic solvent some way towards the polarity of water, whilst still yielding equilibrium constants that could be measured. In addition, we have been investigating the chemosensory effects of volatile organic compounds, VOCs, on humans, 30 and it became necessary to attempt to find if the VOCs associated with each other at the site of action. Octan-1-ol was a solvent with solvation properties close to those of the receptor site, association through hydrogen bonding was likely to be the main associative process, and hence a study of hydrogen bonding in octan-1-ol was indicated. Note that through this work, we refer to dry octanol and not to water-saturated octanol.
Methodology
The compounds we wished to study were simple alkanols, fluoroalkanols, ketones, amides, etc. The usual infra-red method of obtaining equilibrium constants cannot be used with octan-1-ol solvent, several of the compounds have no chromophore thus ruling out methods that use UV/vis specta as the analytical method, and so we devised a new method that uses headspace gas liquid chromatography, GLC, as the analytical method. Before starting on experiments with octan-1-ol solvent, we determined a few equilibrium constants with hexadecane solvent as a check on the method.
Assume that a dilute solution of a solute X and an inert standard substance D in a given solvent is contained in a closed vial, so that X and D will distribute between the solvent and the gas phase above the solvent (the headspace). The equilibrium concentrations of X and D in solution are related to those in the headspace through
| (9) |
| (10) |
where KX and KD are the gas-solvent partition coefficients. When concentrations in the gas phase and in solution are in the same units, say mol dm−3, these coefficients are dimensionless. If a volume of the headspace is sampled and analyzed by GLC, the relative concentrations of X and D in the headspace will be related to their GLC peak areas, AX and AD through
| (11) |
where KGLC is a proportionality constant. Then the relative concentrations of X and D in solution are given by
| (12) |
| (13) |
where KG is a ‘global’ proportionality constant. Now if a non-volatile compound, Y, that hydrogen bonds with X is introduced into the solution, the free concentration of X will be reduced, whilst the concentration of D remains the same. The new concentration of X, CX(solution)’, is given by
| (14) |
Then from eqs 13 and 14, the final equation for X is,
| (15) |
The advantage of introducing an inert standard, D, is that the method does not depend on the volume of headspace analyzed, and the reduction in concentration of X due to complexation with Y can be determined simply from the GLC peak areas before and after introduction of Y, without any calibration at all. The only check required is that the GLC detector response should be linear over the concentration ranges of X and D used in the experiments. Of course, the initial concentration of X in solution must always be larger than the solution concentration of Y. In the present work, X was always a volatile hydrogen bond acid, and Y was an involatile hydrogen bond base.
Results and Discussion
The GLC method can, in principle, be used for any solvent and any pair of acids and bases. The only restriction is that GLC peaks of the volatile components X and D must be separated from the GLC solvent peak, which in the case of a volatile solvent will be very much larger than the peaks due to X and D. To obtain measurable equilibrium constants, we used quite strong hydrogen bond acids, including 1,1,1,3,3,3-hexafluoro-2-methylpropan-2-ol (HFMP), 1,1,1,3,3,3-hexafluoropropan-2-ol (HFIP), and perfluoro-tert-butanol (PFTB), and quite strong hydrogen bond bases. For each acid-base pair, the hydrogen bond acid was the volatile compound used for the GLC analysis. No experiments were carried out with PFTB against 1,1,3,3-tetramethylguanidine because the two appeared to react. Values of log K for the various pairs of acids and bases are given in Tables 2 and 3. Our estimated error in log K is 0.05 log units.
TABLE 2.
Values of log K for the 1:1 Hydrogen Bond Complexation of Solutes in Hexadecane Solvent at 298 K.
| Hydrogen bond acid | Hydrogen bond base | Log K | αH2 | βH2 |
|---|---|---|---|---|
| pentan-1-ol | nitrobenzene | −0.103 | 0.336 | 0.341 |
| pentan-1-ol | nonan-2-one | 0.470 | 0.336 | 0.510 |
| pentan-1-ol | acetophenone | 0.286 | 0.336 | 0.511 |
| pentan-1-ol | dimethylsulfoxide | 1.186 | 0.336 | 0.775 |
| pentan-1-ol | triethylphosphate | 1.450 | 0.336 | 0.793 |
TABLE 3.
Values of log K for the 1:1 Hydrogen Bond Complexation of Solutes in Octan-1-ol Solvent at 298 K.
| Hydrogen bond acid | Hydrogen bond base | Log K | αH2 | βH2 | αH2 *βH2 |
|---|---|---|---|---|---|
| 2-fluoroethanol | dimethylformamide | 0.026 | 0.396 | 0.663 | 0.262 |
| 2-fluoroethanol | dimethylacetamide | −0.023 | 0.396 | 0.730 | 0.289 |
| 2-fluoroethanol | dimethylsulfoxide | 0.099 | 0.396 | 0.775 | 0.307 |
| 2-fluoroethanol | triethylphosphate | 0.150 | 0.396 | 0.792 | 0.314 |
| 2-fluoroethanol | 1,1,3,3-tetramethylguanidine | 0.240 | 0.396 | 0.929 | 0.368 |
| 2-fluoroethanol | hexamethylphosphoramide | 0.520 | 0.396 | 1.000 | 0.396 |
| 2,2,2-trifluoroethanol | dimethylformamide | 0.436 | 0.567 | 0.663 | 0.376 |
| 2,2,2-trifluoroethanol | dimethylacetamide | 0.514 | 0.567 | 0.730 | 0.414 |
| 2,2,2-trifluoroethanol | dimethylsulfoxide | 0.505 | 0.567 | 0.775 | 0.439 |
| 2,2,2-trifluoroethanol | triethylphosphate | 0.484 | 0.567 | 0.792 | 0.449 |
| 2,2,2-trifluoroethanol | 1,1,3,3-tetramethylguanidine | 0.673 | 0.567 | 0.929 | 0.527 |
| 2,2,2-Trifluoroethanol | hexamethylphosphoramide | 0.780 | 0.567 | 1.000 | 0.567 |
| HFMPa | dimethylformamide | 0.664 | 0.655 | 0.663 | 0.434 |
| HFMP | dimethylacetamide | 0.757 | 0.655 | 0.730 | 0.478 |
| HFMP | dimethylsulfoxide | 0.798 | 0.655 | 0.775 | 0.506 |
| HFMP | triethylphosphate | 0.909 | 0.655 | 0.792 | 0.519 |
| HFMP | 1,1,3,3-tetramethylguanidine | 1.009 | 0.655 | 0.929 | 0.608 |
| HFMP | hexamethylphosphoramide | 1.261 | 0.655 | 1.000 | 0.655 |
| HFIPb | dimethylformamide | 0.957 | 0.771 | 0.663 | 0.511 |
| HFIP | dimethylacetamide | 0.994 | 0.771 | 0.730 | 0.563 |
| HFIP | dimethylsulfoxide | 1.042 | 0.771 | 0.775 | 0.597 |
| HFIP | triethylphosphate | 1.095 | 0.771 | 0.792 | 0.611 |
| HFIP | 1,1,3,3-tetramethylguanidine | 0.928 | 0.771 | 0.929 | 0.716 |
| HFIP | hexamethylphosphoramide | 1.544 | 0.771 | 1.000 | 0.771 |
| PFTBc | dimethylformamide | 0.851 | 0.88 | 0.663 | 0.583 |
| PFTB | dimethylacetamide | 0.962 | 0.88 | 0.730 | 0.642 |
| PFTB | dimethylsulfoxide | 0.824 | 0.88 | 0.775 | 0.682 |
| PFTB | triethylphosphate | 1.295 | 0.88 | 0.792 | 0.697 |
| PFTB | hexamethylphosphoramide | 1.691 | 0.88 | 1.000 | 0.880 |
1,1,1,3,3,3-Hexafluoro-2-methylpropan-2-ol (HFMP)
1,1,1,3,3,3-Hexafluoropropan-2-ol (HFIP).
Perfluoro-tert-butanol (PFTB).
The results for hexadecane solvent are straightforward. A regression on the lines of eq 6 leads to eq 16 where the coefficients are commensurate with those found for solvents hexane/heptane and cyclohexane. Although there are only five points, eq 16 demonstrates that our novel method of headspace analysis does indeed yield correct values of log K.
| (16) |
The log K values in octan-1-ol can be regressed against the term αH2 *βH2, see Table 3, and lead to eq 17
| (17) |
In eq 17 we omitted the pair of compounds HFIP/1,1,3,3-tetramethylguanidine and PFTB/dimethylsulfoxide, which were considerable outliers.
In order to increase the number of solvents for a comparison with octan-1-ol, we surveyed the literature and were able to retrieve enough log K values to obtain the coefficients in eq 7 for several other solvents, as shown in Table 1.
For a number of solvents we had to fix the constant, c = −1.10 to obtain any reasonable fit. The correlation coefficient then has no meaning. One reason for the somewhat poor statistics for some of the equations is that we have not considered any family dependencies. A more detailed analysis, for log K values in solvents for which there is considerable data, shows that the coefficients in eq 7 depend slightly on the nature of the hydrogen bond base.12 However the equations for the aprotic solvents in Table 1 confirm that the constant in eq 7 is always near to −1.10 for aprotic solvents that are not too polar.
We have equations for four of the solvents studied by Cook et al., 28 and can use our equations based on eq 7 to predict the log K values for complexation between perfluoro-tert-butanol (αH2= 0.88) and tri-n-butylphosphine oxide (βH2 = 0.934) as shown in Table 4. There is reasonable agreement between observed and predicted values.
TABLE 4.
Observed and Predicted log K values for 1:1 Hydrogen Bond Complexation between Perfluoro-tert-butanol and Tri-n-butylphosphine oxide
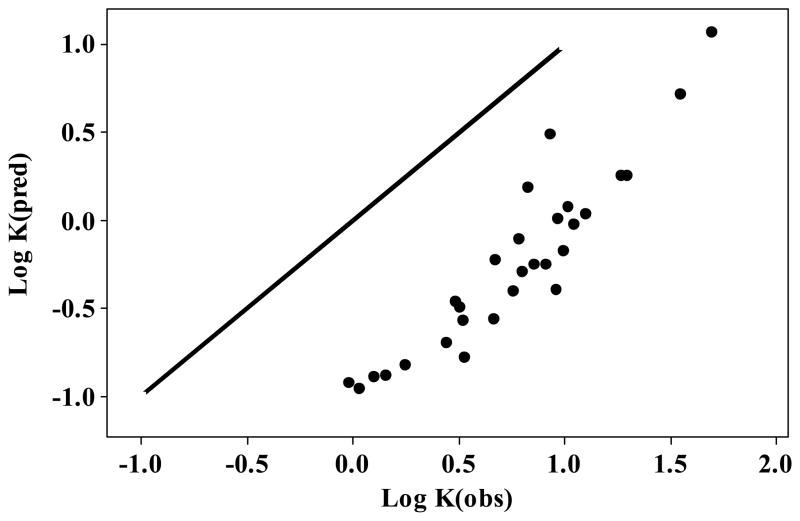
We can also use Hunter’s eq 8 to predict log K values in solvent octan-1-ol (αH2= 0.328 and βH2= 0.46). Fig 1 shows a plot of predicted log K values against the observed values given in Table 3; the line is that of unit slope. All the predicted values from eq 8 are far too small. It is not surprising that eq 8 fails to predict log K values in a hydroxylic solvent. Eq 8 uses αH2 and βH2 values for a compound as a solvent that are taken as values for the compound as a solute. Now this may be a useful approximation for aprotic compounds, but it is not a valid approximation for hydroxylic compounds that are associated as bulk liquids. A comparison of αH2 and βH2 values with the Kamlet-Taft acidities α1 and basicities β1 for solvents 31, 32 is shown in Table 5, and illustrates the differences for the alcoholic associated solvents.
FIGURE 1.
A plot of log K for 1:1 association in octan-1-ol predicted on eq 8, against observed values of log K, from Table 3; the line is that of unit slope.
TABLE 5.
Differences in Hydrogen Bond Acidity and Basicity for Associated Compounds
| Compound | α1 | αH2 | βH1 | βH2 |
|---|---|---|---|---|
| hexane | 0.00 | 0.00 | 0.00 | 0.00 |
| diethyl ether | 0.00 | 0.00 | 0.45 | 0.47 |
| triethylamine | 0.00 | 0.00 | 0.67 | 0.71 |
| methanol | 1.09 | 0.33 | 0.73 | 0.41 |
| ethanol | 0.88 | 0.33 | 0.80 | 0.44 |
| pentan-1-ol | 0.73 | 0.33 | 0.88 | 0.46 |
| water | 1.16 | 0.35 | 0.50 | 0.38 |
If eq 8 cannot be used to deal with log K values in octan-1-ol, it is very doubtful if it can be used for log K values in water. Unfortunately, there are very few measurements available for 1:1 hydrogen bond association in water between solutes with one site of action. Pekary 33 lists values for association between a number of phenols and pyridine, and Stahl and Jencks 34 collected literature data on association between neutral solutes and carboxylate anions, and also measured association constants between a number of protonated amines and the phenolate anion. They used an equation first proposed by Hine 35, 36 to analyze their data on association between the conjugate base of a proton acid and the conjugate acid of a proton base,
| (18) |
Hine 36 suggested that τ was between zero and 0.057 in water; and c was taken by Hine as log (55) = 1.74 and by Stahl and Jencks as log (2*55) = 2.04. Our values of αH2 and βH2 are related to equilibrium constants by a factor of 4.636, see eq 5. Since pKa is – log Ka, any equation on the lines of eq 18 but based on αH2 and βH2 rather than on pK values should have a slope between zero and −0.057* 4.636 = −0.264 for solvent water.
We give in Table 6 log K values of Pekary, 33 and those listed by Stahl and Jencks 34 and measured by them, together with the relevant values of αH2 and beta;H2. We have no values for ionic species, but we have recently obtained the overall hydrogen bond acidity, A, and the overall hydrogen bond basicity, B, for carboxylate anions, phenolate anions and protonated amine cations.37, 38 For monofunctional species, A and B (for solutes) can be used as approximations to αH2 and βH2 (for solutes). Stahl and Jencks34 give results for two monofunctional protonated amines, HOCH2CH2NH3+ and HONH3+ and a number of difunctional protonated amines such as +H3NCH2CH2CH2NH3+. We can take αH2 for HOCH2CH2NH3+ as A for CH3CH2CH2NH3+, but can make no approximation for the other protonated amines.
TABLE 6.
1:1 Hydrogen Bond Association Constants in Water at 298 K
| H-bond acid | H-bond base | K | log K | αH2 | βH2 | αH2*βH2 | Ref |
|---|---|---|---|---|---|---|---|
| phenol | acetate | 0.47 | −0.328 | 0.596 | 2.930 | 1.746 | 34 |
| formic acid | formate | 0.25 | −0.602 | 0.700 | 2.500 | 1.750 | 34 |
| acetic acid | acetate | 0.40 | −0.398 | 0.580 | 2.930 | 1.699 | 34 |
| RNH3+ | phenolate | 0.20 | −0.700 | 1.400 | 2.120 | 2.968 | 34 |
| phenol | pyridine | 0.60 | −0.222 | 0.596 | 0.625 | 0.373 | 33 |
| 4-methylphenol | pyridine | 0.69 | −0.161 | 0.569 | 0.625 | 0.356 | 33 |
| 2-iodophenol | pyridine | 0.57 | −0.244 | 0.400 | 0.625 | 0.250 | 33 |
| 4-iodophenol | pyridine | 0.61 | −0.215 | 0.679 | 0.625 | 0.424 | 33 |
The data in Table 6 yield eq 19, where the slope, m, is now negative and lies between zero and −0.264, exactly in accord with the suggestion of Hine.36 An explanation of the negative slope is that the stronger is the solute hydrogen bond acid or hydrogen bond base, the more it interacts with the water solvent than with the other solute base or acid.
| (19) |
Stahl and Jencks 34 also measured 1:1 hydrogen bond association constants of a series of bases against the ethylenediamine dication as the hydrogen bond acid. We have no value of αH2 for the dication, but give in Table 7 the log K values, together withβH2 for the hydrogen bond bases. What little correlation there is between log K and βH2 suggests that again the slope is negative.
TABLE 7.
1:1 Hydrogen Bond Association Constants in Water at 298 K against the Ethylenediamine Dication 34
| H-Bond base | log K | βH2 | pKa |
|---|---|---|---|
| 4-methoxyphenolate | −0.06 | 2.26 | 10.27 |
| phenolate | −0.09 | 2.12 | 9.99 |
| 4-chlorophenolate | −0.16 | 2.38 | 9.38 |
| 3-nitrophenolate | −0.21 | 2.25 | 8.36 |
| 4-acetylphenolate | −0.22 | 2.38 | 8.05 |
| 4-nitrophenolate | < −0.70 | 2.09 | 7.18 |
| benzoate | < −1.00 | 2.88 | 4.21 |
The negative slope in eq 7 for water solvent shows how difficult it is to measure 1:1 hydrogen bonding in water. For all the other solvents we have studied, the slope in eq 7 is positive, so that it is often possible to increase log K by using stronger hydrogen bond bases and hydrogen bond acids. However, as shown by Scott et al.,39 solutes that are proton acids such as 4-nitrophenol can yield proton transfer complexes and not hydrogen bond complexes in polar solvents. For water as solvent, it is not possible to increase log K simply by increasing the hydrogen bond acidity and basicity of the solutes. Even though eq 7 is approximate only, it suggests that log K cannot be greater than about - 0.1, whatever the strength of the hydrogen bond acid and hydrogen bond base, for 1:1 hydrogen bond association between mono-functional solutes in water. We stress that our assessment is specifically for 1:1 hydrogen bond association between solutes where there is only one site of attachment. Banerjee et al. 40 have suggested a very large equilibrium constant between methyl glyoxal and ascorbic acid in water, where there are multiple sites of attachment in the 1:1 complex.
Mitterhauszerová et al. 41 have found equilibrium constants for 1:1 complexation of 1-naphthol with purine derivatives in water, that are orders of magnitude larger than those found by Pekary 33 and Stahl and Jencks. 34 Thus for caffeine, K = 73. The results of Mitterhauszerova et al. 41 seem inconsistent with the analysis of Hine 35, 36 or the results of Pekary 33 and of Stahl and Jencks. 34 On the other hand, Cussler 42 has interpreted the diffusion experiments on ε-caprolactam in water carried out by Cussler and Dunlop 43 as evidence of a hydrogen bonded dimer with log K = −0.30. With αH2 = 0.383 and βH2 = 0.715 for the secondary amide N-methylacetamide, we can calculate from eq 19 that a 1:1 hydrogen bond complex would have log K = −0.19, in reasonable agreement with Cussler’s value. 42
It is of some interest to evaluate the factors that lead to the different values of log K found in the gas phase, in non-polar solvents and in solvents such as water and octanol-1-ol. As an example, we consider TFE and propanone, for which the 1:1 hydrogen bond association constant in the gas phase is 53.10 We can deduce the corresponding values in other solvents from eq 7, the coefficients in Table 1, and values of αH2= 0.567 for TFE and βH2= 0.497 for propanone. Then knowing the gas-solvent partition coefficients, L, from the gas phase to solvents (see eq 20, below), we can calculate the gas-solvent partition coefficients of the complex, as shown in Table 8. Note that we usually use K for the gas-water partition coefficient, but here we use L to avoid confusion with the 1:1 equilibrium constant. The values of log L are a quantitative measure of the solvation free energy of the various species, since ΔG°= −RTln L. As the solvent becomes more polar, so are the reactants more solvated. The complex is also more solvated in the polar solvents, but not as much as the reactants, thus leading to a diminution in values of log K.
TABLE 8.
The Solvation of Reactants and Complex in the 1:1 Hydrogen-Bonding of 2,2,2-Trifluoroethanol and Propanone
| Log L | ||||||
|---|---|---|---|---|---|---|
| Solvent | Log K | Log Ks/Kg | TFE | Propanone | Reactants | Complex |
| gas phase | 1.72 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| cyclohexane | 1.21 | −0.51 | 1.40 | 1.86 | 3.26 | 2.75 |
| hexane | 0.99 | −0.58 | 1.49 | 1.92 | 3.41 | 2.83 |
| CCl4 | 0.98 | −0.74 | 1.85 | 2.34 | 4.19 | 3.45 |
| benzene | 1.00 | −0.74 | 2.28 | 2.62 | 4.90 | 4.16 |
| chlorobenzene | 0.82 | −0.90 | 2.23 | 2.64 | 4.87 | 3.97 |
| bromobenzene | 0.80 | −0.92 | 2.17 | 2.62 | 4.79 | 3.87 |
| dichloromethane | 0.41 | −1.31 | 2.73 | 3.20 | 5.93 | 4.62 |
| trichloromethane | 0.22 | −1.50 | 2.65 | 3.26 | 5.91 | 4.41 |
| benzonitrile | 0.16 | −1.56 | 3.30 | 2.85 | 6.15 | 4.59 |
| octanol | 0.10 | −1.62 | 3.53 | 2.31 | 5.84 | 4.22 |
| water | −0.19 | −1.91 | 3.50 | 2.95 | 6.45 | 4.54 |
It is possible to estimate properties of the 1:1 complex itself. We have developed 44, 45 an equation for the correlation and estimation of gas-solvent partition coefficients, L, eq 20,
| (20) |
The dependent variable in eq 20 is log L for a set of solutes in a given solvent. The independent variables are solute descriptors as follows. 44, 45 E is an excess molar refraction in cm3 mol−1/10. S is a combined dipolarity/polarizability descriptor. A is the overall solute hydrogen bond acidity, B is the overall solute hydrogen bond basicity and L is the logarithm of the solute gas-hexadecane partition coefficient at 298K. It is important to note that these measures of overall solute hydrogen bond acidity and basicity (A and B) are not the same as the 1:1 hydrogen bond acidities and basicities. The set of coefficients, c, e, s, a, b and l characterise the given solvent and are determined by multiple linear regression analysis. Values of log L for 2,2,2-trifluoroethanol and for propanone in the various solvents were calculated from their known solute descriptors 44,45 and the known 46 solvent coefficients in eq 19. We have values of log L for the complex in eleven different solvents, Table 8, and for all these solvents we have an equation on the lines of eq 20. It is then possible to use the eleven equations and the eleven values of log L to calculate the unknown E, S, A, B and L values for the complex. These are in Table 9 together with values for TFE and propanone. Of considerable interest is that the complex still has the property of a hydrogen-bond acid, with A = 0.29; although this is considerably less than that of TFE, it is not far from the hydrogen-bond acidity of an alcohol.
TABLE 9.
Properties of the 1:1 Complex between 2,2,2-Trifluoroethanol and Propanone.
| Solute | E | S | A | B | L |
|---|---|---|---|---|---|
| 2,2,2-trifluoroethanol | 0.015 | 0.60 | 0.57 | 0.25 | 1.224 |
| propanone | 0.179 | 0.70 | 0.04 | 0.49 | 1.696 |
| complex | 0.373 | 0.99 | 0.29 | 0.46 | 2.657 |
| ethanol | 0.246 | 0.42 | 0.37 | 0.48 | 1.485 |
| tert-butanol | 0.180 | 0.30 | 0.31 | 0.60 | 1.963 |
We can now better understand the log L values in Table 8. The complex is neither a strong hydrogen-bond acid (A = 0.29) nor a strong hydrogen-bond base (B = 0.46), although it has considerable dipolarity/dipolarizability (S = 0.99). There are almost no interactions between the basic function in the complex and acidic functions in the aprotic solvents (only dichloromethane and trichloromethane have any hydrogen-bond acidity) and there are not very large interactions between the acidic function in the complex and the basic functions in the aprotic solvents. As the aprotic solvents become more polar, there will be enhanced dipole-dipole interaction, leading to a gradual increase in log L. In the case of octanol and water, there will be considerable acid-base and base-acid interactions, but in water, these are to a large extent offset by the hydrophobic effect – unlike nonaqueous solvents, the solubility of solutes in water decreases with size. Exactly similar analyses could be carried out for any of the 1:1 complexes between the hydrogen bond acids and hydrogen bond bases in Table 3.
We are now in a position to evaluate any possible influence of association of solutes on their chemosensory effects. We take octan-1-ol as a model biophase and use eq 7 to estimate the percentage association in octan-1-ol between typical volatile organic compounds, VOCs, for which odor detection thresholds, ODT, and nasal pungency thresholds have been determined for the vapors. Recent studies by Cometto-Muñiz and Abraham have shown that ODTs are mostly in the range of about 0.1–100 ppb (v/v) for VOCs, such as alkylbenzenes, 47 aliphatic aldehydes, 48 aliphatic ketones, 49 alcohols 50 and alkyl acetates. 51 For these solutes, the concentration in octan-1-ol is around 3,000 times that in the gas phase 52 when both concentrations are expressed in mol dm−3, so that the ODT thresholds correspond to octan-1-ol concentrations of 1.0 *10 −6 to 100*10−6 in mol dm−3. For a mixture of VOCs containing a hydrogen bond base such as butanone (βH2 = 0.48) and a hydrogen bond acid such as ethanol (αH2= 0.33) the association constant between the two solutes, from eq 17, is log K = - 0.27, so that at a concentration of 100*10−6 for each solute, less than 0.01% of the solute will exist as the 1:1 hydrogen bond complex. Nasal pungency thresholds, NPT, are much larger than the corresponding ODT values, by on average about three log units, 30 so that NPT thresholds correspond to octan-1-ol concentrations between 1.0 *10 −3 to 100*10−3 in mol dm−3. Then with log K as −0.27, at concentrations from 1.0 *10 −3 to 100*10−3 in each solute, the amount present as a 1:1 hydrogen bond complex will be from 0.05% to 5.0%. Thus if octan-1-ol can be taken as a reasonable model for the biological site of action for odor detection thresholds and nasal pungency thresholds, we can use eq 7 to deduce that there will be little association between VOCs at the site of action. This conclusion is important when assessing, via ODTs and NPTs, the rules governing the odor and nasal pungency potency of mixtures of VOCs. 53–55
Experimental Section
Octan-1-ol was stored over molecular sieve and transferred to flasks sealed with serum caps using hypodermic syringes in order to minimize contact with the atmosphere. Headspace analysis was carried out using a GLC column of 12% Carbowax 20M on Chromosorb W. The column temperature ranged from 363 K to 413 K depending on the analytes. Peak areas were calculated using an in-house computer program. The linearity of the GLC detector was checked as follows. Solutions of the hydrogen bond acid, X, and the inert standard decane, D, were made up by weight with concentrations ranging from about 0.02 to 0.5 mol dm−3. A 10 cm3 sample of the solution was added to a specially constructed flask of volume 150 cm3 with a narrow neck closed by a serum cap. The solutions were allowed to equilibrate at 298 K, 3 cm3 of the headspace was removed by means of a 5 cm3 gas-tight syringe and injected onto the GLC column. The only practical difficulty we encountered was in the thermostatting of the flasks used to contain the solvent mixtures. The tops of the flasks projected slightly above the water used in the thermostat with the result that any volatile component in solution could condense around the inside of the serum caps. To avoid this, the tops of the vials and serum caps were covered with a layer of thin plastic sheet over all of the thermostat so that the temperature of the serum caps did not drop below that of the thermostat liquid. We then extracted vapor samples by penetrating both the plastic sheet and the serum caps with the hypodermic syringe. The syringe was kept at 298 K prior to use in order to avoid condensation in the syringe. Plots of peak areas against solution concentrations were linear over the concentration range used for decane and for all the acids, X. Incidentally, this demonstrates that all the acids were unassociated in octanol at the concentrations used. For the typical acid, HFIP, the gas to octanol partition coefficient is 575 and so the solution concentrations correspond to concentrations in the gas phase of from 3.5*10−5 to 8.7*10−4 mol dm−3. Even at the highest gaseous concentration, eq 7 together with the constants in Table 1 for the gas phase, indicates that less then 0.1% of HFIP is associated in the gas phase. Self-association is more likely to take place in aprotic solvents such as n-hexadecane. To avoid such risk, the concentration of pentan-1-ol was kept close to 0.05 mol dm−3 in hexadecane. For the measurement of equilibrium constants, solutions of X and D were made up as above in two flasks which were then thermostatted for 30 min, and shaken from time to time. The involatile base, Y, was then added to one of the flasks so that the concentration of Y was always less than X. After another 60 min headspace samples were taken from each of the flasks and analyzed by GLC. A second set of samples was taken after another 30 min.
Conclusions
We have devised a new method for the determination of 1:1 hydrogen bond association constants between a hydrogen bond acid solute and a hydrogen bond base solute that can be used with octan-1-ol as a solvent. Analysis of 27 association constants leads to an equation on exactly the same lines as those for association in aprotic, rather non-polar, solvents, but with a much smaller slope. The equation shows that, in general, 1:1 hydrogen bonding in octan1-ol is much reduced compared to association in these aprotic solvents. Examination of literature data on 1:1 hydrogen bonding in water leads to the conclusion that not only is such hydrogen bonding much less than it is even in octan-1-ol, but that the extent of hydrogen bonding actually diminishes as the solutes become stronger hydrogen bond acids and stronger hydrogen bond bases. For simple 1:1 hydrogen bonding between mono-functional solutes, it seems impossible to obtain log K values greater than about −0.1 log units. The equation for association in octan-1-ol can be used to assess the extent of association between solutes in a biological phase.
Acknowledgments
We are grateful to Professor Michel Berthelot (University of Nantes - France) for his helpful comments and suggestions. This work has been supported in part by research grants R01 DC 002741 and DC 005003 from the National Institute on Deafness and Other Communication Disorders, National Institutes of Health, USA.
References
- 1.Joesten MD, Schaad LJ. Hydrogen Bonding. Marcel Dekker; New York: 1974. [Google Scholar]
- 2.Green RD. Hydrogen Bonding by C-H Groups. Macmillan; London: 1974. [Google Scholar]
- 3.Abboud JL, Bellon L. Ann Chim. 1970;5:63–74. [Google Scholar]
- 4.Abraham MH, Duce PP, Grellier PL, Prior DV, Morris JJ, Taylor PJ. Terahedron Lett. 1988;29:1587–1590. [Google Scholar]
- 5.Abraham MH, Grellier PL, Prior DV, Duce PP, Morris JJ, Taylor PJ. J Chem Soc Perkin Trans. 1989;2:699–711. [Google Scholar]
- 6.Abraham MH, Grellier PL, Prior DV, Morris JJ, Taylor PJ, Laurence C, Berthelot M. Terahedron Lett. 1989;30:2571–2574. [Google Scholar]
- 7.Abraham MH, Grellier PL, Prior DV, Morris JJ, Taylor PJ. J Chem Soc Perkin Trans. 1990;2:521–529. [Google Scholar]
- 8.Abraham MH, Grellier PL, Prior DV, Taft RW, Morris JJ, Taylor PJ, Laurence C, Berthelot M, Doherty R, Kamlet MJ, Abboud JLM, Sraidi K, Guiheneuf G. J Am Chem Soc. 1988;110:8534–8536. [Google Scholar]
- 9.Raevsky OA, Grigor’ev VYu, Kireev DB, Zefirov NS. Quant Struct-Act Relationships. 1992;11:49–63. [Google Scholar]
- 10.Marco J, Orza JM, Notario R, Abboud JLM. J Am Chem Soc. 1994;116:8841–8842. [Google Scholar]
- 11.Abraham MH, Berthelot M, Laurence C, Taylor PJ. J Chem Soc, Perkin Trans. 1998;2:187–191. [Google Scholar]
- 12.Abraham MH, Berthelot M. unpublished work. [Google Scholar]
- 13.Cabot R, Hunter CA, Varley LM. Org Biomol Chem. 2010;8:1455–1462. doi: 10.1039/b921003b. [DOI] [PubMed] [Google Scholar]
- 14.Demeter A, Bérces T. J Phys Chem A. 2005;109:2043–2049. doi: 10.1021/jp045495j. [DOI] [PubMed] [Google Scholar]
- 15.Dharmalingam K, Ramachandran K, Sivagurunathan P, Kalamse GM. J Chem Eng Data. 2007;52:265–269. [Google Scholar]
- 16.Dharmalingam K, Ramachandran K, Sivagurunathan P, Kalamse GM. Spectrochim Acta A. 2008;69:467–470. doi: 10.1016/j.saa.2007.04.023. [DOI] [PubMed] [Google Scholar]
- 17.Dharmalingam K, Jalbout A. J Mol Liq. 2008;141:17–18. [Google Scholar]
- 18.Sivagurunathan P, Khan FLA, Ramachandran K. Z Phys Chem (München) 2007;221:273–280. [Google Scholar]
- 19.Spencer JN, Sweigart JR, Brown ME, Bensing RL, Hassinger TL, Kelly W, Housel DL, Reisinger GW, Relfsnyder DS, Glelm JE, Peiper JC. J Phys Chem. 1977;81:2237–2240. [Google Scholar]
- 20.Spencer JN, Campanella CL, Harris EM, Wolbach WS. J Phys Chem. 1985;89:1888–1891. [Google Scholar]
- 21.Spencer JN, Modarress KJ, Nachlis WL, Hovick JW. J Phys Chem. 1986;90:4443–4447. [Google Scholar]
- 22.Spencer JN, Grushow A, Ganunis TF, Allott KN, Kneizys SP, Willis H, Puppala S, Salata CM, Zafar AI, Stein BJ, Hahn LC. J Soln Chem. 1989;18:471–480. [Google Scholar]
- 23.Biczok L, Gupta N, Linschitz H. J Am Chem Soc. 1997;119:12601–12609. [Google Scholar]
- 24.Joris L, Mitsky J, Taft RW. J Am Chem Soc. 1972;94:3438–3445. [Google Scholar]
- 25.Libuś W, Męcik M, Sułek W. J Soln Chem. 1977;6:865–879. [Google Scholar]
- 26.Vasin SV. Zhur Fiz Khim. 1985;59:1921–1924. [Google Scholar]
- 27.Abraham MH, Duce PP, Prior DV, Barratt DG, Morris JJ, Taylor PJ. J Chem Soc Perkin Trans. 1989;2:1355–1375. [Google Scholar]
- 28.Cook JL, Hunter CA, Low CMR, Perez-Velasco A, Vinter JG. Angew Chem Int Ed. 2007;46:3706–3709. doi: 10.1002/anie.200604966. [DOI] [PubMed] [Google Scholar]
- 29.Hunter CA. Angew Chem Int Ed. 2004;43:5310–5324. doi: 10.1002/anie.200301739. [DOI] [PubMed] [Google Scholar]
- 30.Abraham MH, Sánchez-Moreno R, Cometto-Muñiz JE, Cain WS. Chem Senses. 2007;32:711–719. doi: 10.1093/chemse/bjm038. [DOI] [PubMed] [Google Scholar]
- 31.Gonçalves RMC, Simöes AMN, Albuquerque LMPC, Rosés M, Ràfols C, Bosch E. J Chem Res (S) 1993:214–215. [Google Scholar]; J Chem Res (M) 1993:1380–1388. [Google Scholar]
- 32.Marcus Y. Chem Soc Revs. 1993:409–416. [Google Scholar]
- 33.Pekary AE. Biophys Chem. 1978;7:325–338. doi: 10.1016/0301-4622(78)85009-1. [DOI] [PubMed] [Google Scholar]
- 34.Stahl N, Jencks WP. J Am Chem Soc. 1986;108:4196–4205. [Google Scholar]
- 35.Hine J. Physical Organic Chemistry. 2. McGraw-Hill; NewYork: 1962. pp. 81–84. [Google Scholar]
- 36.Hine J. J Am Chem Soc. 1972;94:5766–5771. [Google Scholar]
- 37.Abraham MH, Acree WE., Jr J Org Chem. 2010;75:1006–1015. doi: 10.1021/jo902388n. [DOI] [PubMed] [Google Scholar]
- 38.Abraham MH, Acree WE., Jr J Org Chem. 2010;75:3021–3026. doi: 10.1021/jo100292j. [DOI] [PubMed] [Google Scholar]
- 39.Scott R, De Palma D, Vinogradov S. J Phys Chem. 1968;72:3192–3201. [Google Scholar]
- 40.Banerjee D, Koll A, Filarowski A, Bhattacharyya SP, Mukherjee S. Spectrochim Acta A. 2004;60:1523–1526. doi: 10.1016/j.saa.2003.08.022. [DOI] [PubMed] [Google Scholar]
- 41.Mitterhauszerová L, Králová K, Krasnec L. Chem Zvesti. 1981;35:525–531. [Google Scholar]
- 42.Cussler EL. Mass Transfer in Fluid Systems. 3. Cambridge University Press; Cambridge, UK: 2009. Diffusion. [Google Scholar]
- 43.Cussler EL, Jr, Dunlop PJ. Aust J Chem. 1966;19:1661–1665. [Google Scholar]
- 44.Abraham MH. Chem Soc Revs. 1993;22:73–83. [Google Scholar]
- 45.Abraham MH, Ibrahim A, Zissimos AM. J Chromatogr A. 2004;1037:29–47. doi: 10.1016/j.chroma.2003.12.004. [DOI] [PubMed] [Google Scholar]
- 46.Abraham MH, Smith RE, Luchtefeld R, Boorem AJ, Luo R, Acree WE., Jr J Pharm Sci. 2010;99:1500–1515. doi: 10.1002/jps.21922. [DOI] [PubMed] [Google Scholar]
- 47.Cometto-Muñiz JE, Abraham MH. Neuroscience. 2009;161:236–248. doi: 10.1016/j.neuroscience.2009.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cometto-Muñiz JE, Abraham MH. Chem Senses. 2010;35:289–299. doi: 10.1093/chemse/bjq018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Cometto-Muñiz JE, Abraham MH. Behav Brain Res. 2009;201:207–215. doi: 10.1016/j.bbr.2009.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Cometto-Muñiz JE, Abraham MH. Pharmacol Biochem Behav. 2008;89:279–291. doi: 10.1016/j.pbb.2007.12.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cometto-Muñiz JE, Cain WS, Abraham MH, Gil-Lostes J. Physiol Behav. 2008;95:658–667. doi: 10.1016/j.physbeh.2008.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Abraham MH, Le J, Acree WE, Jr, Carr PW, Dallas AJ. Chemosphere. 2001;44:855–863. doi: 10.1016/s0045-6535(00)00288-5. [DOI] [PubMed] [Google Scholar]
- 53.Cometto-Muñiz JE, Cain WS, Abraham MH. Behav Brain Res. 2005;156:115–123. doi: 10.1016/j.bbr.2004.05.014. [DOI] [PubMed] [Google Scholar]
- 54.Cometto-Muñiz JE, Cain WS, Abraham MH. Indoor Air. 2004;14(Suppl 8):108–117. doi: 10.1111/j.1600-0668.2004.00297.x. [DOI] [PubMed] [Google Scholar]
- 55.Cometto-Muñiz JE, Cain WS, Abraham MH. Exp Brain Res. 2004;158:196–206. doi: 10.1007/s00221-004-1890-5. [DOI] [PMC free article] [PubMed] [Google Scholar]