Algorithm 1 Projection of q ∈ 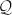 to to 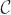
| |||
| 1: | Initialize l(q)i = 1n. Let ε > 0. | ||
| 2: | while ‖l(q)‖ > ε do | ||
| 3: | Compute l(q)i = −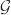 i(q), i = 1, …, n. i(q), i = 1, …, n. |
||
| 4: | Calculate the Jacobian matrix, Ji,j = 〈∇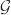 i(q), ∇ i(q), ∇ j(q)〉 as follows, j(q)〉 as follows,
|
||
| 5: | Solve the equation J(q)xT = lT(q) for x. | ||
| 6: | Update , δ > 0. | ||
| 7: |
|
||
| 8: | end while | ||

An official website of the United States government
Here's how you know
Official websites use .gov
A
.gov website belongs to an official
government organization in the United States.
Secure .gov websites use HTTPS
A lock (
) or https:// means you've safely
connected to the .gov website. Share sensitive
information only on official, secure websites.