Translationally optimal codons associate with aggregation-prone sites in proteins

Abstract

We analyze the relationship between codon usage bias and residue aggregation propensity in the genomes of four model organisms, E. coli, yeast, fly, and mouse, as well as the archaeon Halobacterium species NRC-1. Using the Mantel-Haenszel procedure, we find that translationally optimal codons associate with aggregation-prone residues. Our results are qualitatively and quantitatively similar to those of an earlier study where we found an association between translationally optimal codons and buried residues. We also combine the aggregation-propensity data with solvent-accessibility data. Even though the resulting data set is small, and hence statistical power low, results indicate that the association between optimal codons and aggregation-prone residues exists both at buried and at exposed sites. By comparing codon usage at different combinations of sites (exposed, aggregation-prone sites vs. buried, non-aggregation-prone sites; buried, aggregation-prone sites vs. exposed, non-aggregation-prone sites), we find that aggregation propensity and solvent accessibility seem to have independent effects of (on average) comparable magnitude on codon usage. Finally, in fly, we assess whether optimal codons associate with sites at which amino-acid substitutions lead to an increase in aggregation propensity, and find only a very weak effect. These results suggest that optimal codons may be required to reduce the frequency of translation errors at aggregation-prone sites that coincide with certain functional sites, such as protein–protein interfaces. Alternatively, optimal codons may be required for rapid translation of aggregation-prone regions.

1 Introduction

Translation is an error-prone process [1]. Translation errors occur at frequencies of several misincorporations per 10,000 codons translated; precise error rates vary over nearly an order of magnitude among codons [2]. Selection for correct protein structure and function should cause codons with reduced error rates to be used more frequently at sites at which translation errors would be particularly disruptive. This selection pressure is called selection for translational accuracy [3].

To identify a signal of accuracy selection in a genome, one needs a measure of how disruptive translation errors are at specific sites. Early studies used as such measure evolutionary conservation [3–5] and, to a very limited extent, specific functional sites [3]. By testing for an association between codon usage and evolutionary conservation, Akashi found evidence for translational accuracy selection in Drosophila [3]. Later, others found similar results in Escherichia coli, yeast, worm, and mammals [4, 5]. More recently, Zhou et al. considered solvent accessibility and change in free energy upon mutation as measures of a site’s sensitivity to translation errors [6]. They found in E. coli, yeast, fly, and mouse that translationally optimal codons associate both with buried residues and with residues that are required for protein stability. This finding supports the hypothesis that translational accuracy selection minimizes the misfolding of mistranslated proteins [5], likely to avoid protein aggregation.

However, selection for translational accuracy is not the only mechanism that can lead to an association of codon-usage bias with certain structural features of the expressed protein. Codons corresponding to rare tRNAs can stall the ribosome, and these translational pauses may either facilitate co-translational folding or, as in the case of translation errors, lead to misfolding and aggregation [7–12].

Under protein aggregation, misfolded proteins can adopt amyloid or amorphous structure [13, 14]. Thus, aggregation primarily arises from the improper interactions between misfolded proteins, leading to gain-of-toxicity or loss-of-function of the protein [15, 16]. Because protein aggregation tends to incur fitness costs, a gene’s amino-acid sequence is under selection pressure to minimize aggregation [16–19].

Here, we investigate whether codon-usage bias is linked to sites with specific aggregation propensity. Residue aggregation propensities are predicted by the Zyggregator method [20]. The Zyggregator algorithm predicts aggregation propensity on the basis of several intrinsic properties of amino-acid sequences, including amino acid scales for secondary structure formation, hydrophobicity, and charge, and the presence of hydrophobic patterns and of gatekeeper residues. We consider four model organisms, Escherichia coli, Saccharomyces cerevisiae, Drosophila melanogaster, and Mus musculus, as well as the archaeon Halobacterium species NRC-1. Our analysis makes extensive use of both concepts and data sets previously developed in [6].

We test whether translationally optimal codons associate with aggregation-prone sites, i.e., sites that are particularly likely to be involved in protein-protein aggregation. We also test whether optimal codons associate with sites at which translation errors are expected to cause an increase in the protein’s aggregation propensity. Surprisingly, we find that optimal codons associate much more strongly with sites of high aggregation propensity than with sites at which aggregation propensity is expected to increase upon amino-acid substitution. The observed association may reflect the kinetic requirement to translate aggregation-prone regions rapidly to avoid protein misfolding. Alternatively, the codon usage might actually be determined by a correlation of the aggregation propensity with other factors, such as the propensity to form protein-protein interfaces [21, 22], rather than by aggregation propensity itself. We elaborate on these possibilities in the Discussion.

2 Materials and Methods

We obtained genomic sequences from the following sources: the Comprehensive Microbial Resource (http://cmr.tigr.org/) for E. coli, the Saccharomyces Genome Database (ftp://genome-ftp.stanford.edu/) for S. cerevisiae, the Eisen Lab (http://rana.lbl.gov/drosophila/) for D. melanogaster, Ensembl (http://www.ensembl.org/) for M. musculus, and GenBank (accession number AE004437) for Halobacterium species NRC-1.

We used a previously published computational algorithm (Zyggregator method, [20]) to predict the aggregation propensity for each residue. In the Zyggregator method, the aggregation propensity at each site i is measured as a Z-score $Z_i^{\text{agg}}$. This Z-score measures how likely site i is to be involved in protein aggregation relative to a site in a randomly generated protein sequence. We considered residues with Z_agg > 1 as aggregation-prone and others as non-aggregation-prone, unless otherwise specified.

We calculated $Z_i^{\text{agg}}$ scores for all residues in organisms’ proteomes, as given by UniProt (http://www.uniprot.org/). We retained only those gene sequences for which the UniProt sequence exactly matched the translated version of the genomic DNA sequence. Our final data set contained 2,983 E. coli genes, 3,253 S. cerevisiae genes, 2,624 D. melanogaster genes, 11,419 M. musculus genes, and 1,604 genes for Halobacterium sp. NRC-1.

We obtained optimal codons for E. coli, yeast, mouse, and fly from [6]. In [6], codons were defined as optimal if they showed a statistically significant increase in frequency in the 5% most highly expressed genes compared to the 5% of genes with the lowest expression level. For Halobacterium sp. NRC-1, we determined optimal codons on the basis codon usage bias as measured by the adjusted effective number of codons (ENC′) [23]. See caption to Table S1 for details.

We also obtained residue solvent accessibilities for proteins with known 3D structure from [6]. After combining the aggregation data with the structural data, our data set contained 588 E. coli genes, 132 S. cerevisiae genes, 208 D. melanogaster genes, and 570 M. musculus genes. For Halobacterium sp. NRC-1, we repeated the procedures of [6] to match genes to protein structures but found too few structures to carry out a meaningful analysis.

To estimate to what extent translation errors at a site would affect aggregation propensity, we defined a sensitivity S_i. S_i measures the mean change in the protein’s aggregation propensity Z^agg upon mutation at site i. Z^agg is defined as [20]

$$Z^{\text{agg}}=\frac{{\sum }_{j=1}^L{Z}_j^{\text{agg}}\theta (Z_j^{\text{agg}})}{{\sum }_{j=1}^L\theta (Z_j^{\text{agg}})},$$ (1)

where L is the length of the protein and θ(x) is the Heaviside step function, θ (x) = 1 for x ≥ 0 and θ(x) = 0 otherwise. Upon mutation at a site i, the values $Z_j^{\text{agg}}$ change at several sites surrounding site i. We refer to the protein’s aggregation propensity upon mutation at site i to amino acid a as Z^agg(σ_i → a) and calculate it according to Eq. (1) but with appropriately modified $Z_j^{\text{agg}}$ values. The sensitivity S_i is then

$$S_i=\frac{1}{19}\sum _{a\ne {\sigma }_i}[Z^{\text{agg}}({\sigma }_i\to a)-Z^{\text{agg}}],$$ (2)

where the sum runs over all amino acids but the one originally at site i. Values of S_i > 0 mean that mutations at site i tend to increase the protein’s aggregation propensity, whereas values S_i ≤ 0 mean that mutations at site i tend to decrease the protein’s aggregation propensity. Because calculation of S_i is computationally expensive, we carried it out only for an arbitrary selection of 845 genes from fly.

Statistical analysis was done as described [6]. In brief, we stratified the data by gene and synonymous codon family within each gene and constructed a separate 2×2 contingency table for each stratum. We then combined either the tables for all genes and a given codon family or the tables for all genes and all codon families into an overall analysis, using the Mantel-Haenszel procedure [24, 25]. We excluded contingency tables whose sum of all four entries was 0 or 1.

We carried out all statistical analyses using the software R [26]. In the analyses of individual amino acids, we corrected for multiple testing using the false-discovery-rate method of Benjamini and Hochberg [27], as implemented in the R function p. adjust().

3 Results

3.1 Association between codon optimality and aggregation propensity

We first tested for an association between codon usage and protein aggregation propensity. Our analysis was based on contingency tables. For all amino acids with more than one codon, we classified the corresponding codons into optimal and not optimal (see Materials and Methods; in some cases, we could not identify optimal codons for specific amino acids; we excluded those amino acids from the analysis). Similarly, we classified all sites in a genome at which a particular amino acid occurred as either aggregation-prone or not aggregation prone (see Materials and Methods). For each amino acid in each gene, we then constructed a 2 × 2 contingency table, counting how often optimal or non-optimal codons coincided with either aggregation-prone or non-aggregation-prone sites (Table 1). For each amino acid, we then combined the individual tables for each gene into an overall analysis, using the Mantel-Haenszel procedure, and calculated a joint odds ratio (O_joint). A value of O_joint greater than 1 signifies a preference for optimal codons at aggregation-prone sites.

Table 1.

Example of a 2×2 contigency table for amino acid Gly in one particular gene of E. coli.

	Codon	Aggregation-prone sites	Non-aggregation-prone sites
Optimal	GGU, GGC	6	23
Not-optimal	GGA, GGG	3	14

Note.—Codons GGU and GGC are optimal codons for amino acid Gly in E. coli. The odds ratio of optimal codon usage between aggregation-prone and non-aggregation-prone sites is $\frac{6/23}{3/14}=1.22$ for this contigency table. Because there is one table of Gly per one gene, we applied the Mantel-Haenszel procedure to calculate the joint odds ratio for all tables of Gly across all genes.

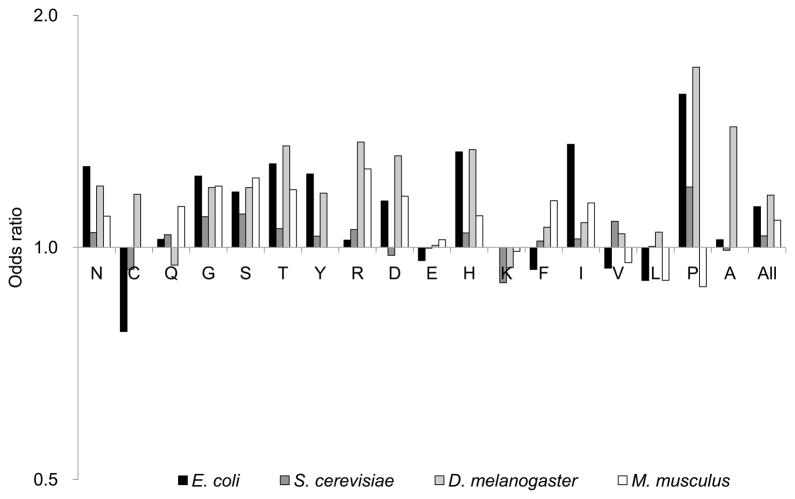
We found that 16 of 18 amino acids showed, in at least one species, a significant preference for optimal codons at aggregation-prone residues (Tables 2 and S1 and Figure 1). One amino acid (Val) in E. coli, one (Lys) in yeast, three (Leu, Pro, and Val) in mouse, and two (Asp, Lys) in Halobacterium sp. NRC-1 showed a significant preference for optimal codons at non-aggregation-prone sites. Of a total of 84 association tests, 42 showed a significant preference for aggregation-prone optimal codons, while only 7 showed a significant preference for non-aggregation-prone optimal codons.

Table 2.

Odds ratio of optimal codon usage between aggregation-prone and non-aggregation-prone sites for each amino acid

AA	E. coli	S. cerevisiae	D. melanogaster	M. musculus
Ala	0.99	0.99	1.43***	–
Arg	1.11(*)	1.06	1.37***	1.26***
Asn	1.10**(*)	1.05*(*)	1.20***	1.10***
Asp	1.09**	0.98	1.31***	1.17***
Cys	1.04	0.94(*)	1.17***	–
Gln	1.04	1.04	0.95	1.13***
Glu	1.06	1.00	1.01	1.02
Gly	1.24***	1.10***	1.20***	1.20***
His	1.18***	1.04	1.34***	1.10***
Ile	1.07***	1.03	1.08***	1.14***
Leu	0.98	1.00	1.05**	0.91***
Lys	–	0.90***	0.94	0.99
Phe	1.03	1.02	1.06**	1.15***
Pro	1.10	1.20	1.71***	0.89*
Ser	1.17***	1.10***	1.20***	1.23***
Thr	1.29***	1.06***	1.35***	1.19***
Tyr	1.22***	1.03	1.18***	–
Val	0.86***	1.08***	1.04*	0.96***
Overall	1.07***	1.03***	1.17***	1.08***

Note. —AA: amino acid; -: no optimal codon. Significance levels:

^***P < 0.001;

^**P < 0.01;

^*P < 0.05.

Significance levels in parentheses disappear after correction for multiple testing.

Figure 1.

Joint odds ratio of optimal codon usage between aggregation-prone and non-aggregation-prone sites for each amino acid. The odds ratios were calculated by the Mantel-Haenszel procedure. The y-axis represents odds ratio and the axis was transformed into the log-2 scale. The x-axis represents amino acids that are ordered according to the amino acid property (Hydrophilic: N, C, Q, G, S, T, Y; Charged: R, D, E, H, K; Hydrophobic: F, I, V, L, P, A) [56].

For each species, we also used the Mantel-Haenszel procedure to combine all 2×2 contingency tables for all genes and all amino acids into a single overall odds ratio. We found a statistically significant association between optimal codons and aggregation-prone sites in all species (odds ratio 1.07, P = 5.9 ×10⁻²⁹ for E. coli; 1.03, P = 5.3 × 10⁻¹⁴ for S. cerevisiae; 1.17, P < 10⁻¹⁰⁰ for D. melanogaster; 1.08, P < 10⁻¹⁰⁰ for M. musculus; 1.22, P = 1.2 × 10⁻⁴³ for Halobacterium sp. NRC-1; see also Tables 2 and S1).

3.2 Relative importance of aggregation propensity and solvent accessibility

Tartaglia and coworkers [20, 21] suggested that even though particular regions in a protein may have a high aggregation propensity, these regions are unlikely to be promote aggregation from the folded state if they are buried after protein folding. That is, the effective aggregation propensity is altered depending on protein structure. In line of this reasoning, we asked whether the association between optimal codons and aggregation-prone sites was affected by solvent accessibility.

First, we investigated exposed sites and buried sites separately. The exposed sites were divided into two groups, aggregation-prone and non-aggregation-prone (Figure 2). We found that, although the significance for most amino acids disappeared using the Mantel-Haenszel procedure, the joint odds ratio of optimal codon usage between aggregation-prone and non-aggregation-prone sites remained larger than 1 for more than half of the amino acids (Table 3). We repeated the same analysis for buried sites and found similar results (Table 3). It seems that the loss of statistical significance for most amino acids was primarily due to the reduction in data-set size when incorporating protein structural information. By incorporating solvent accessibility data, gene numbers decreased from 2,983 to 588 in E. coli, from 3,253 to 132 in yeast, from 2,624 to 208 in fly, and from 11,419 to 570 in mouse. We found that the odds ratios for data sets with structural information were quantitatively similar to odds ratios in data sets of similar size obtained by randomly sampling from the data sets without structural information (data not shown).

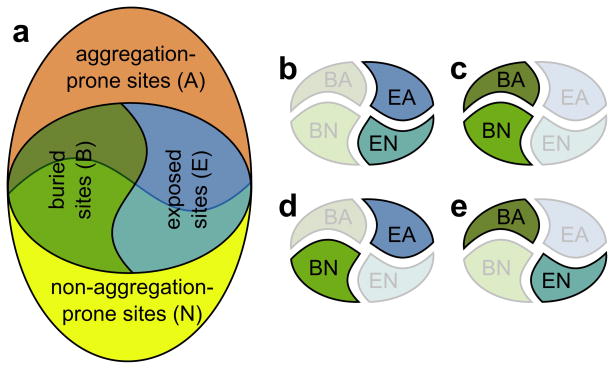
Figure 2.

Venn diagram illustrating the various analyses reported in Table 3. (a) We classify all sites in an organism’s coding sequences as either aggregation-prone (A) or non-aggregation-prone (N). For a subset of sites, we have structural information. We classify these sites as either buried (B) or exposed (E). (b) Analysis of codon usage by aggregation propensity for exposed sites only. (c) Analysis of codon usage by aggregation propensity for buried sites only. (d) Comparison of codon usage among exposed, aggregation-prone and buried, non-aggregation-prone sites. (e) Comparison of codon usage among buried, aggregation-prone and exposed, non-aggregation-prone sites.

Table 3.

Odds ratio of optimal codon usage between exposed-aggregation-prone and exposed-non-aggregation-prone sites, between buried-aggregation-prone and buried-non-aggregation-prone sites, between exposed-aggregation-prone and buried-non-aggregation-prone sites, and between buried-aggregation-prone and exposed-non-aggregation-prone sites for each amino acid

	E. coli				S. cerevisiae				D. melanogaster				M. musculus
AA	EA-EN	BA-BN	EA-BN	BA-EN	EA-EN	BA-BN	EA-BN	BA-EN	EA-EN	BA-BN	EA-BN	BA-EN	EA-EN	BA-BN	EA-BN	BA-EN
Ala	1.02	1.05	1.07	0.93	0.70	0.92	0.57(**)	0.99	1.45(*)	1.08	1.25	1.22	–	–	–	–
Arg	1.02	1.04	1.06	1.01	1.57	1.13	1.56	0.90	1.31	0.93	1.28	1.22	1.33(*)	1.16	1.26	1.44*
Asn	1.27*(*)	1.02	0.94	1.46***	0.88	1.12	0.94	1.16	1.17	1.63*(*)	1.28	1.57*(*)	1.14	1.12	0.88	1.41***
Asp	1.15	1.18	1.05	1.22(*)	1.03	0.84	1.10	0.78	1.65***	1.64*(*)	1.87***	1.50*(*)	1.11	1.23	1.08	1.30*(*)
Cys	0.78	1.03	1.13	0.83	1.60	0.76	0.29(*)	0.84	0.54	1.03	1.04	0.82	–	–	–	–
Gln	1.02	0.89	0.84	1.13	1.08	1.14	1.31	1.42	0.75	0.94	0.84	0.91	1.04	1.27	0.98	1.42*(*)
Glu	0.96	1.00	0.90	1.07	1.01	1.35	1.15	1.26	0.91	0.82	0.97	0.91	0.89	1.05	0.83	1.05
Gly	1.24(*)	1.31**(*)	1.19	1.37***	0.94	0.94	0.70(*)	1.32(*)	0.92	1.11	0.97	1.10	1.11	1.25**(*)	1.08	1.23**(*)
His	1.33(*)	1.50**(*)	1.25	1.33(*)	1.59	0.99	1.72	1.05	0.93	1.63(*)	1.91(*)	1.10	1.30(*)	1.15	1.17	1.26
Ile	1.36(*)	1.09	1.36(**)	1.10	0.94	0.68*(*)	1.23	1.00	1.27	0.93	1.02	1.06	1.07	1.15*	1.05	1.24*(*)
Leu	0.91	0.81***	0.82(*)	0.96	0.84	1.03	0.86	1.18	0.87	1.07	0.82	1.14	0.76*(*)	0.87**	0.82(*)	0.86*(*)
Lys	–	–	–	–	0.73	0.83	0.63(*)	0.90	0.73(*)	0.47(*)	0.87	0.72	1.08	1.36(*)	1.08	1.42*(*)
Phe	0.94	1.03	1.02	1.03	1.03	1.10	0.78	1.15	0.71	1.02	0.68	0.82	0.85	1.19**	1.03	1.18
Pro	1.58	0.69	1.59	0.83	2.35	0.18	2.74	0.19	2.88	0.17	5.08	0.21	0.56	0.51	0.63	0.44
Ser	1.18	1.19(*)	0.88	1.70***	0.96	1.53*(*)	0.98	1.58**(*)	1.10	0.74(*)	0.87	1.01	1.09	1.24*(*)	0.90	1.40***
Thr	1.28*(*)	1.23**	1.07	1.55***	0.91	0.93	0.82	1.06	1.09	1.36*(*)	1.09	1.40*(*)	1.31**(*)	1.20*(*)	1.12	1.37***
Tyr	1.25	1.27**	1.30(*)	1.06	0.79	1.04	1.13	1.01	1.18	1.30	1.12	1.26	–	–	–	–
Val	0.94	0.86**	0.94	0.75***	1.27	1.27(*)	1.24	1.53*(*)	1.01	1.07	0.77	1.21	1.05	0.96	0.91	1.03
Overall	1.13***	1.03	1.02	1.13***	0.95	1.03	0.93	1.15**(*)	1.06	1.08*(*)	1.06	1.15***	1.08*(*)	1.08***	1.00	1.19***

Note. —AA: amino acid; EA: exposed and aggregation-prone sites; BN: buried and non-aggregation-prone sites; BA: buried and aggregation-prone sites; EN: exposed and non-aggregation-prone sites; -: no optimal codon. Significance levels:

^***P < 0.001;

^**P < 0.01;

^*P < 0.05.

Significance levels in parentheses disappear after correction for multiple testing.

Second, we assessed whether solvent accessibility or aggregation propensity exerted the stronger selection pressure on codon usage. We considered the odds ratio of optimal codon usage between exposed-aggregation-prone and buried-non-aggregation-prone sites (Figure 2d). Assuming that optimal codons associate with both buried and aggregation-prone sites, an odds ratio > 1 in this test indicates that aggregation propensity dominates while an odds ratio < 1 indicates that solvent accessibility dominates. Our results indicated that either factor can be more important, depending on species and amino acid (Table 3, columns labeled “EA-BN”, i.e., exposed and aggregation-prone vs. buried and non-aggregation-prone). Considering all odds ratios, regardless of significance level, we found that the odds ratios of at least 6 amino acids in each species were smaller than 1 while the odds ratios of at least 8 amino acids in each species were larger than 1 (Table 3). Therefore, neither factor clearly dominated in all species.

Finally, we asked to what extent aggregation propensity and solvent accessibility independently shape codon usage. To address this question, we computed the odds ratio of optimal codon usage between buried-aggregation-prone and exposed-non-aggregation-prone sites (Figure 2e). We found that the overall odds ratio in each species is larger than 1 and statistically significant (odds ratio 1.13, P = 7.0×10⁻⁹ for E. coli; 1.15, P = 7.1×10⁻⁴ for S. cerevisiae; 1.15, P = 2.5 ×10⁻⁵ for D. melanogaster; 1.19, P = 1.8 ×10⁻¹⁵ for M. musculus; see also Table 3, columns labeled “BA-EN”, i.e., buried and aggregation-prone vs. exposed and non-aggregation-prone). More importantly, when comparing the odds ratios for individual amino acids to those where we considered aggregation-propensity or solvent accessibility individually (Table S2), we found that the BA-EN odds ratios minus 1 are roughly the sum of the individual odds ratios minus 1. For example, in E. coli, for Asn, A-N odds are 1.21, B-E odds are 1.34, BA-EN odds are 1.46. Likewise, for Ser, A-N odds are 1.26, B-E odds are 1.42, BA-EN odds are 1.70; for Thr, A-N odds are 1.26, B-E odds are 1.22, BA-EN odds are 1.55. And, consistent with this pattern, for Val, A-N odds are 0.85, B-E odds are 0.88, BA-EN odds are 0.75. Similar patterns exist in the other species. Thus, residue aggregation propensity and solvent accessibility seem to affect synonymous codon usage independently of each other.

All results reported so far were carried out with a cutoff of Z_agg > 1 to classify aggregation-prone sites. We also considered a cutoff of Z_agg > 0, which is more lenient but at the same time provides for a more powerful statistical analysis because aggregation-prone sites are more common under this definition. We found that our results were not strongly sensitive to the specific cutoff used (Tables S3 and S4).

3.3 Sensitivity to translation errors

If selection for codon usage is driven by the cost of translation errors, then we might assume that the change in aggregation propensity upon amino-acid substitution at a site i is more strongly correlated with codon usage than the site’s aggregation propensity itself. To evaluate this hypothesis, we defined a sensitivity S_i to amino-acid substitution at site i. S_i is the mean change between the aggregation propensity of a mutated protein and the one of the wild-type protein (see Materials and Methods).

We calculated S_i for all sites in an arbitrary selection of 845 fly genes. We defined sites with S_i > 0 as sensitive to amino-acid substitution and all other sites as not sensitive. We constructed 2×2 contingency tables of the number of optimal/non-optimal codons coinciding with sensitive or not-sensitive sites. We stratified by gene and amino acid, as before, and used the Mantel-Haenszel procedure to calculate joint odds ratios. An odds ratio > 1 means that optimal codons associate with sensitive sites.

We found very little evidence for an association between optimal codons and sensitive sites (Table S5). The overall odds ratio was 1.03 (P = 0.03). Over half of the amino acids tested showed no significant association whatsoever. Only Ala, Arg, and Pro showed a positive association between optimal codons and sensitive sites, while Lys and Thr showed a negative association (after correction for multiple testing). This result is in stark contrast to the association between optimal codons and the raw aggregation propensity, which for fly was positive and highly significant for nearly all amino acids (Table 2). Thus we conclude that, at least for fly, the raw aggregation propensity rather than the sensitivity to amino-acid substitutions drives codon usage. We provide some potential explanations for this result in the Discussion.

4 Discussion

We have found that translationally optimal codons associate with aggregation-prone sites in a bacterium, an archaeon, and three eukaryotes. With the exception of the archaeon, where we had insufficient data, we have found that this association occurs both at buried and at exposed sites. We have also found that our results are not merely caused by the tendency of optimal codons to associate with buried sites. Instead, buriedness and aggregation propensity seem to influence codon usage independently of each other. Finally, for fly we have found that sensitivity, a measure of how much the aggregation propensity of a protein increases upon mutation of a site, associates much more weakly with optimal codons than the aggregation propensity itself does.

Our results add to a growing list of mechanisms by which synonymous codons are under selective pressure. Selection on synonymous sites has been found to be linked to transcription [28], splicing [29–31], thermodynamic stability of DNA and RNA secondary structure [32–37], efficient and accurate translation [3–6, 12, 38–49], protein co-translational folding [7–11, 50], and translation initiation [51–53].

We obtained translationally optimal codons from [6]. In that study, optimal codons were identified as those codons that were significantly more frequent in highly expressed genes than in genes with low expression level. (For Halobacterium sp. NRC-1, we determined optimal codons using a similar method as in [6] but comparing genes with high and low codon bias instead of expression level.) This method of identifying optimal codons can go wrong in specific cases. If there are speed-accuracy tradeoffs so that the faster codon is less accurate and vice versa, the method of [6] may identify the faster rather than the more accurate codon. If an organism experiences both selection for translation speed and translational accuracy, then it is possible that the most rapidly translated codon is the most abundant one in highly expressed genes but that the most accurately translated codon is preferred at sites at which translation errors need to be avoided. As an example, the odds ratios for Val in E. coli are always significantly below 1, regardless of whether we correlate codon usage with aggregation propensity or with solvent accessibility. We used as optimal codons for Val in E. coli the two codons GUA and GUU. On the basis of tRNA-abundance measurements [54] and modeling of the translation process [55], we expect that these two codons are optimal for translation speed. Therefore, we suspect that the codons for Val that are the most rapidly translated in E. coli are not the most accurately translated ones for Val in this species.

As we had seen in previous work [6], there is no consistent pattern among organisms of which amino acids show a significant signal of translational accuracy selection. We could not identify any specific biophysical property of amino acids (such as volume, hydrophobicity, or charge) that would explain either the observed odds ratios or the associated P values. In previous work [6], the best predictor for P values was amino-acid frequency, indicating that much of the variation in the observed results may simply be due to lack of statistical power for rarer amino acids. It is also possible that different amino acids are under selection for translational accuracy in different protein structures, so that the Mantel-Haenszel results for a given organism may be partially driven by the specific composition of that organism’s proteome.

It is intriguing to discuss possible mechanisms that cause optimal codons to associate with aggregation-prone sites but not with sites that show an increase of aggregation propensity upon mutation. A first possibility is that, since the Zyggregator aggregation propensities are correlated with other physico-chemical properties [20], the features that we use to predict aggregation propensity do not only identify regions that have a high tendency to form aberrant inter-molecular contacts but also predict segments that are involved in the formation of functional contacts [21, 22]. Indeed, the location of interfaces in molecular complexes correlates strongly with the presence of peaks in the aggregation profiles [22]. Thus, optimal codons may be protecting protein–protein interfaces rather than aggregation-prone sites per se. Moreover, we have found that aggregation-prone sites tend to evolve slower than sites that are not aggregation prone (Zhou, unpublished). Thus, the same mechanism that selects against genetic mutations at aggregation prone sites—this mechanism may or may not be related to functional contacts—may also be sensitive to translation errors and thus select for optimal codons at aggregation-prone sites.

An alternative possibility is that optimal codons might be selected for rapid rather than accurate translation, because slow-folding regions could be particularly susceptible to mis-folding in case the ribosome stalls. In favor of this type of explanation, we have found that regions characterized by high aggregation propensities are associated with slow folding rates (Tartaglia and Vendruscolo, unpublished). Aggregation-prone regions of the nascent chain already outside the ribosome would remain available for a prolonged time to form dysfunctional inter-molecular interactions, since they would not be protected from aggregation by the folding process. In this case, it would be the necessity to prevent aggregation during the co-translational folding process, rather than the protection in the native state, that would primarily cause the selective pressure. This view is consistent with the very weak correlation that we found between optimal codon usage and solvent exposure of aggregation-prone regions. On the other hand, if translation speed rather than accuracy was under selection, we would expect the rapidly translated codons for Val in E. coli to associate with aggregation-prone sites, not with sites that are not aggregation prone. In this context, it would be interesting to investigate whether aggregation-prone regions are more frequent in C-terminal regions rather than in N-terminal regions, which are the first to emerge during biosynthesis. Future studies will have to disentangle these various possibilities to determine why optimal codons associate with aggregation-prone sites.