Small-angle solution scattering using the mixed-mode pixel array detector

A fast-readout pixel array detector is evaluated for small-angle X-ray scattering experiments.

Abstract

Solution small-angle X-ray scattering (SAXS) measurements were obtained using a 128 × 128 pixel X-ray mixed-mode pixel array detector (MMPAD) with an 860 µs readout time. The MMPAD offers advantages for SAXS experiments: a pixel full-well of >2 × 10⁷ 10 keV X-rays, a maximum flux rate of 10⁸ X-rays pixel⁻¹ s⁻¹, and a sub-pixel point-spread function. Data from the MMPAD were quantitatively compared with data from a charge-coupled device (CCD) fiber-optically coupled to a phosphor screen. MMPAD solution SAXS data from lysozyme solutions were of equal or better quality than data captured by the CCD. The read-noise (normalized by pixel area) of the MMPAD was less than that of the CCD by an average factor of 3.0. Short sample-to-detector distances were required owing to the small MMPAD area (19.2 mm × 19.2 mm), and were revealed to be advantageous with respect to detector read-noise. As predicted by the Shannon sampling theory and confirmed by the acquisition of lysozyme solution SAXS curves, the MMPAD at short distances is capable of sufficiently sampling a solution SAXS curve for protein shape analysis. The readout speed of the MMPAD was demonstrated by continuously monitoring lysozyme sample evolution as radiation damage accumulated. These experiments prove that a small suitably configured MMPAD is appropriate for time-resolved solution scattering measurements.

1. Introduction

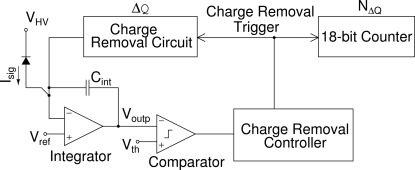
The mixed-mode pixel array detector (MMPAD) is the result of a collaboration between Area Detector Systems Corporation and the Cornell University X-ray detector group to produce a detector for high-throughput macromolecular crystallography (Vernon et al., 2007 ▶; Angello et al., 2004 ▶; Schuette, 2008 ▶). While developed primarily for crystallography, a small-area version (128 pixels × 128 pixels, 19.2 mm × 19.2 mm) of this detector has proven useful for a variety of X-ray experiments. The device is a bump-bonded hybrid of two distinct layers. The first layer is a high-resistivity silicon detector of thickness 500 µm in which X-rays convert to charge. The charge is conveyed via metallic bump-bond connections to pixels in a CMOS readout chip. The readout chip pixels utilize analog integration of charge in conjunction with in-pixel overflow detection and charge removal. During typical operation the programmable signal accumulated per charge removal is set to 115 X-rays with energy of 9.5 keV. The pixel output value is the combination of the analog residual and the count of charge removal operations. A high-level schematic representation of the pixel is shown in Fig. 1 ▶.

Figure 1.

A high-level schematic of the pixel architecture. Photo-charge (I _sig) from the reverse-biased diode is integrated across C _int. When the comparator senses a near-to-overflow condition, a charge removal operation, which increments a count in the 18-bit counter, is triggered. The pixel output at the end of an exposure is the combination of the digital counts (N _ΔQ) and the analog residual (V _outp) (Schuette, 2008 ▶).

Extensive results of X-ray testing of the MMPAD have been presented (Schuette, 2008 ▶) and are summarized in Table 1 ▶. The detector features a maximum flux-rate of 10⁸ X-rays pixel⁻¹ s⁻¹, a sub-pixel point-spread function, a frame rate that exceeds 1 kHz, and a pixel saturation level in 9.5 keV X-rays of 3.3 × 10⁷. The work presented here evaluates the MMPAD for X-ray solution scattering experiments and shows it to be particularly appropriate for time-resolved solution scattering measurements.

Table 1. Parameters of the MMPAD detector used in these experiments.

Efficiencies are calculated from Henke et al. (1993) ▶.

Format	128 × 128 pixels
Pixel size	150 µm × 150 µm
Efficiency at 8 keV	0.99
Efficiency at 11 keV	0.94
Efficiency at 13 keV	0.82
Full-frame readout time	860 µs
Pixel full-well capacity	2.3 × 107 X-rays (9.5 keV)
Maximum flux rate	108 X-rays pixel−1 s−1
Point-spread function	Sub-pixel
RMS pixel read-noise	0.15–0.55 X-rays pixel−1 (9.5 keV)

Small-angle X-ray scattering (SAXS) of macromolecules in solution measures the scattering intensity from a particle as a function of momentum transfer, I(q), averaged over all orientations of the particle. The Fourier inverse of the scattering function gives the pair-distribution function, P(r), which is a measure of the frequency of distances between all possible pairs of points within the particle. Since the pair-distribution function is bounded by the maximum dimension of the particle (D _max), its Fourier inverse, the scattering intensity, has a complete discrete representation at intervals called Shannon channels that are separated by Δq = π/D _max (Shannon & Weaver, 1949 ▶; Svergun & Koch, 2003 ▶). For example, the scattering pattern of a particle with D _max = 50 Å measured from q = 0.02 Å⁻¹ to q = 0.40 Å⁻¹ has six Shannon channels within the curve. The 128 × 128 pixel MMPAD should be able to sufficiently sample this curve. Large area X-ray detectors (∼1000 × 1000 pixels) can be configured to highly oversample small-angle solution scattering curves. Although some oversampling of this curve may be beneficial (Svergun & Koch, 2003 ▶), this often includes increased noise. Since each detector pixel contributes read-noise to the image, distribution of the signal photons among an excessive number of detector pixels can be detrimental to the signal-to-noise ratio.

Time-resolved solution scattering experiments track structural changes during transient events such as changes of oligomeric composition or molecule folding and unfolding (Segel et al., 1999 ▶; Russell et al., 2002 ▶). For example, a stopped-flow mixer may be used to initiate a transient chemical event and the time coordinate is measured by the time difference between the mixing event and the X-ray exposure. For these experiments the time scales of interest range from milliseconds to seconds. Unfortunately the readout time (seconds) of most X-ray detectors limits the number of exposures per mixing run to one, or a few. The use of detectors which read out quickly, such as the MMPAD, would increase the number of time points measured per mixing run and reduce the quantity of sample and the time required for a full data set.

Other fast-readout X-ray area detectors have been designed for SAXS experiments. Examples include a direct detection front-illuminated frame-transfer 1024 × 1024 pixel charge-coupled device (CCD) with a detection efficiency of 49% at 6.9 keV and a 64 Hz full-frame rate (Falus et al., 2004 ▶). Fast-readout phosphor-coupled CCD detectors include the FReLoN development at the ESRF with a 4.2 Hz full-frame rate (Coan et al., 2006 ▶; Labiche et al., 2007 ▶) as well as an electron-multiplying CCD with a full-frame rate of 30 Hz (Nagarkar et al., 2007 ▶). Pixel array detector (PAD) developments include the Pilatus which uses readout pixels that count individual X-rays (Broennimann et al., 2006 ▶). A 100K Pilatus module, 487 × 195 pixels of 172 µm size, with a 333 Hz frame rate has been tested for small-angle scattering at the X33 beamline at DESY. An annular silicon strip detector has been developed at the Advanced Photon Source (Lurgio et al., 2005 ▶). This detector features a 16.67 kHz readout time for the 128 detecting rings with a noise per ring of around ten X-rays of energy 9.5 keV. Prototypes of high-speed-readout fully depleted direct-detection CCDs have been tested at the Advanced Photon Source (Denes et al., 2009 ▶). Back-illuminated direct-detection devices feature sub-pixel point-spread functions and very low noise but may be hindered by a limited dynamic range. Of the devices described above the MMPAD features the second fastest full-frame rate and the highest dynamic range.

Here the functionality of a small-area fast-framing PAD capable of contributing to time-resolved solution SAXS experiments is demonstrated. The read-noise of the MMPAD is compared with, and found to be better than, the read-noise of a typical CCD detector used for solution SAXS experiments. Lysozyme scattering data are then presented which display the detection characteristics of the MMPAD. In §3.3 radiation damage is studied by exploiting the MMPAD high-speed readout to continuously acquire 1000 frames during dosing.

2. Methods and beamline configuration

Solution SAXS measurements were performed at the Cornell High Energy Synchrotron Source (CHESS) G1 station. The G1 station uses multilayer monochromator pairs and horizontal and vertical focusing to maximize the flux to the sample from a wiggler insertion device. The experiments described used a 250 µm × 250 µm beam defined by helium enclosed slits at an energy of 9.55 keV with a bandpass of ΔE/E = 1.5%. An ion chamber before the sample monitored the beam intensity and gave a flux of around 1 × 10¹² photons s⁻¹. Two 25 µm-thick molybdenum attenuators were available upstream to decrease the intensity at the sample by factors of 11× and 120× when necessary. Samples were enclosed between 7.5 µm-thick Kapton windows glued to the faces of acrylic laminate discs with a central bore (Ando et al., 2008b ▶). The discs were 2 mm thick, which sets the sample X-ray interaction path length. Scattered X-rays travelled through an evacuated flight path. A silicon PIN diode beamstop was positioned within the evacuated flight path close to the detector and used to monitor the transmitted intensity.

Solution SAXS measurements were recorded using the previously described MMPAD and a custom-built 1024 × 1024 pixel CCD X-ray detector. The CCD detector fiber-optically couples a gadolinium oxysulfide:Tb (P-43) phosphor screen (Grant Scientific) settled at a density of 15 mg cm⁻² to a scientific-grade blue-enhanced CCD from Eastman Kodak Corporation (KAF-1001E, Rochester, NY, USA). The fiber-optic taper (Incom, Charlton, MA, USA) demagnifies the phosphor image onto the CCD chip by a factor of 2.9, which gives a pixel size of 69.8 µm at the phosphor screen. The read-noise of the detector has been measured as 11 e⁻ pixel⁻¹ while the sensitivity at 5.9 keV has been measured as 13.1 e⁻ X-ray⁻¹. This CCD detector has been successfully applied to SAXS experiments at CHESS (Wedekind et al., 2006 ▶; Ando et al., 2008a ▶).

Silver behenate powder (The Gem Dugout, State College, PA, USA) was used to calibrate all sample-to-detector distances and locate the beam center. A stock solution of lysozyme was prepared by dissolving the lyophilized powder (Sigma-Aldrich L7651 lot 072K7062) in 0.1 M sodium acetate buffer at pH 4.5 (HCl) to yield a final concentration of 25 mg ml⁻¹. A volume of pure buffer solution was also retained for use in solvent background subtraction. Actual solution SAXS measurements were conducted on stock solution diluted to 5 mg ml⁻¹ with matching buffer so as to minimize possible concentration effects on the scattering curve while maintaining a scattering intensity typical of many BioSAXS samples. Unless otherwise noted, samples were at room temperature during data acquisition.

After subtraction of a dark image, two-dimensional detector data from the MMPAD were corrected for local distortions that arise from dopant inhomogeneities in the high-resistivity detector layer (Tlustos et al., 2003 ▶) with an adaptive filtering method (Schuette, 2008 ▶). Two-dimensional data from the CCD detector were corrected for distortions and gain non-uniformity using standard CCD X-ray detector techniques (Barna et al., 1999 ▶). CCD detector data were corrected for frame-to-frame row pedestal shifts by subtracting the mean of a group of pixels at the end of each row that were blocked from X-rays with a lead-tape shield. MMPAD frame-to-frame pedestal shifts were removed by subtraction of the mean of six readout pixels that had a failed bump-bond connection to the detector layer. These pixels were not X-ray sensitive and provided a convenient monitor of the readout pedestal shift. After corrections, two-dimensional detector data were reduced to one-dimensional profiles, I(q _i), [q = 4πsin(θ)/λ, with 2θ the scattering angle and λ the X-ray wavelength] in units of X-rays pixel⁻¹ with a custom suite of programs written in Matlab (The MathWorks Inc., Natick, MA, USA) and C. The q-increment, Δq = q _i+1 − q _i, of the radial integration was configured in the software to be equal for both detectors. A sub-area of the CCD images that matched the area of the MMPAD and the full CCD images were both used for analysis (referred to as ‘cut’ and ‘full-chip’, respectively). To explore the effect of spatial spreading on detection noise, MMPAD images were spatially filtered using a low-pass Gaussian response with standard deviation of 0.23 MMPAD pixels (34 µm) to emulate the point-spread function of the CCD detector. The point-spread function of a similar CCD X-ray detector has been measured to have a full width at half-maximum of 80 µm, which, if approximated as a Gaussian response, has a 34 µm standard deviation (Tate et al., 1995 ▶). MMPAD data processed with this spatial filter are referred to as ‘filtered’. Conversion factors from detector digital-number to X-rays were used to represent the intensity in units of X-rays for more intuitive analysis of limiting noise sources. The scattering profile of water (Orthaber et al., 2000 ▶) was measured to confirm the validity of both the X-ray flux measurements and the detector conversion factors used.

Scattering data from an empty sample cell and with samples of water, silica spheres, lysozyme buffer and lysozyme at a concentration of 5 mg ml⁻¹ were acquired with both detectors. Multiple exposure times and attenuation levels were used for each sample; for radiation-sensitive samples the shortest exposure times and highest attenuation levels were recorded first. Silver behenate calibration images for these comparative measurements gave a sample-to-detector distance of 360 mm and 350 mm for the CCD and MMPAD measurements, respectively. For protein samples the scattering profile was calculated after subtraction of background scattering collected from a matched buffer solution and sample cell. Unless otherwise noted, the PIN diode reading was used to normalize images before subtraction. The GNOM package (Svergun et al., 1988 ▶) was used to produce a smoothed representation of the lysozyme scattering profile and to evaluate the radius of gyration.

3. Experiments and results

3.1. Read-noise

Image noise is due to inherent fluctuations of the electronic circuitry of the detector (read-noise) and to the Poisson fluctuations of the X-ray illumination. At low levels of illumination the read-noise limits the minimum X-ray signal that is detectable. At higher levels of X-ray illumination the X-ray noise increases and the detector read-noise is less significant. For solution scattering experiments detector read-noise is most significant in the wide-angle regime where the scattered signal is low.

To evaluate detector read-noise, images with 100 ms exposure time were acquired without X-ray signal and processed to one-dimensional curves. The dark images were radially integrated because the noise of scattering profiles is more relevant to solution SAXS experimenters than the per-pixel detector noise. From the one-dimensional profile the noise in a range of q increments, q _L to q _H, was measured as the standard deviation of the intensities measured by all q-increments through the range and is represented as σ_profile(q _L, q _H). Fig. 2 ▶ illustrates this method. The beam center and sample-to-detector distance are arbitrary without X-ray signal. These values were chosen to match those of the experiments described later in §3.2. Since the signal collected by each pixel depends on its angular size, a more representative comparison of anticipated signal-to-noise was calculated as the product of the CCD noise measurements with the ratio of the solid angle subtended per pixel at equal sample-to-detector distances, Ω_ratio = A _MMPAD/A _CCD = (150 µm)²/(69.8 µm)² = 4.62, where A _MMPAD and A _CCD are the areas of a single MMPAD and CCD pixel, respectively. Ω_ratio is the multiplicative factor required to scale per-pixel intensities acquired at equal sample-to-detector distances to match the different pixel sizes.

Figure 2.

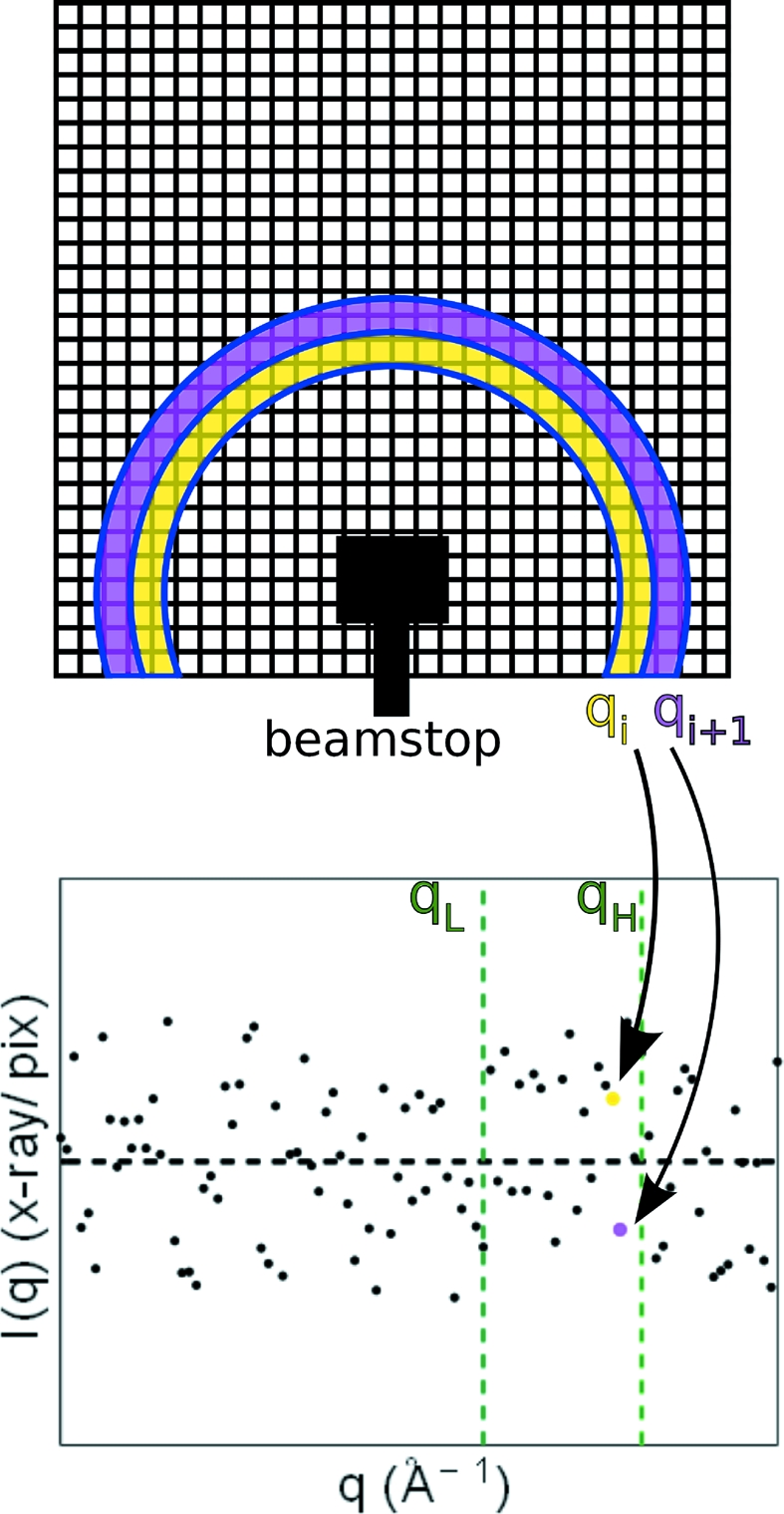
A detector grid (top) and hypothetical one-dimensional I (X-rays pixel⁻¹) versus q profile (bottom) to illustrate the read-noise analysis. The top section shows two q increments, q _i and q _i+1 (the beamstop is drawn to indicate the selected position of the beam center). The plot at the bottom shows a possible one-dimensional profile resulting from radial integration of an image with no illumination. An ideal detector would measure zero at all q increments. Dashed green lines that run vertically display sectioning of the profile into a range of q increments for calculation of the noise σ_profile(q _L,q _H). The black horizontal dashed line shows the detector global pedestal level (mean value).

As a check for consistency, for each range the noise, σ_profile(q _L,q _H), multiplied by the square root of the average of the number of pixels per q-increment, (pixel_count)^1/2, was calculated. The average number of pixels was used since the number of pixels in each increment varies slightly within a range. The product σ_profile(pixel_count)^1/2 should match the portion of the per-pixel read-noise that is not correlated among pixels. The results are shown in Table 2 ▶. The read-noise measurements normalized to pixel area were found to be factors of 12.0, 7.1, 3.9 and 1.7 less for the MMPAD versus ‘full-chip’ measurements of the CCD detector for four ranges of q values studied. The MMPAD read-noise varies across the chip owing to off-chip electronics. This will be addressed in future iterations of the support electronics.

Table 2. Summary of read-noise tests for an exposure time of 100 ms.

The MMPAD read-noise is not constant across the chip owing to off-chip electronics. The last column shows the data for the entire q range but σ_profile(pixel_count)^1/2 is not calculated owing to the large variation in pixels per q increment across the whole range. Frame-to-frame global pedestal variations that remain after correction techniques cause an RMS fluctuation of 0.02 X-rays for the CCD and 0.10 X-rays for the MMPAD.

		q range (qL–qH) (Å−1)				NET
		0.05–0.09	0.09–0.14	0.14–0.24	0.24–0.32	0.05–0.32
MMPAD	σprofile	0.015	0.017	0.027	0.059	0.042
	Mean pixel_count	14.6	22.1	34.5	19.8	24.9
	σprofile(pixel_count)1/2	0.058	0.079	0.16	0.26	–
CCD (cut)	σprofile	0.061	0.054	0.043	0.047	0.052
	σprofileΩratio	0.28	0.25	0.20	0.22	0.24
	Mean pixel_count	58.1	95.8	158.7	130.6	123.8
	σprofile(pixel_count)1/2	0.46	0.53	0.54	0.54	–
CCD (full-chip)	σprofile	0.039	0.026	0.023	0.021	0.027
	σprofileΩratio	0.18	0.12	0.11	0.099	0.13
	Mean pixel_count	207.5	373.2	562.0	680.8	510.2
	σprofile(pixel_count)1/2	0.56	0.50	0.55	0.56	–

Even when the entire area of the CCD is utilized, σ_profile of the MMPAD is less than σ_profileΩ_ratio of the CCD within all q-ranges calculated. These measurements suggest that given a pattern with low photon intensities, where read-noise would be most significant, the MMPAD will outperform the CCD detector. The described evaluation technique does not account for fluctuations in the detector global pedestal level that remain after the previously described correction techniques. Using the same data the frame-to-frame RMS fluctuations of the global pedestal level in units of 9.5 keV X-rays pixel⁻¹ were measured to be 0.10 and 0.02 for the MMPAD and CCD detector, respectively.

3.2. Scattering measurements

To evaluate the quality of captured scattering profiles the technique of Lamb et al. (2008 ▶) was followed to calculate the signal-to-noise ratio (S/N) as

where data is the measured curve and fit is the output from GNOM. For this measurement, to ensure that improper normalization was not interpreted as signal at high q, the buffer normalization factor was determined via comparison of the scattering curve with the standard lysozyme scattering profile distributed with the Crysol package (Svergun et al., 1995 ▶). The results with 100 ms exposure times with and without attenuation are shown for both detectors in Table 3 ▶.

Table 3. Evaluation of the average S/N [equation (1)] from five captures with 100 ms exposure time compared with the calculated smooth GNOM curve. ‘11× att.’ refers to experiments with the beam attenuated by a 25 µm-thick molybdenum attenuator.

		q range (qL–qH) (Å−1)				NET
		0.05–0.09	0.09–0.14	0.14–0.24	0.24–0.32	0.05–0.32
MMPAD	11× att.	21.2	17.6	5.8	0.56	10.1
MMPAD (filtered)	11× att.	28.4	24.9	7.7	0.87	13.2
CCD (full-chip)	11× att.	22.5	19.4	5.1	0.47	10.5
CCD (cut)	11× att.	11.3	10.8	3.1	0.51	5.9
MMPAD	No att.	75.1	60.3	23.7	4.0	38.3
MMPAD (filtered)	No att.	107.2	74.3	32.6	5.1	50.5
CCD (full-chip)	No att.	147.2	110.9	35.4	7.6	68.3
CCD (cut)	No att.	63.8	48.1	17.9	3.0	30.6

Calculation of this metric at different q-ranges allows for comparisons in regimes of different dominant noise sources. At high q (0.24–0.32 Å⁻¹) and with 11× attenuation the scattered intensity is low and detector read-noise contributes significantly to the measured noise. At lower q photon Poisson fluctuations are the dominant noise source. Measured photon noise has been shown to be lower for a detector with a broader point-spread function (Moy, 2000 ▶; Ponchut et al., 2005 ▶). As such, photon noise was anticipated to be attenuated by the CCD detector more than by the MMPAD since the CCD detector has a broader point-spread function. For all q ranges and both attenuation levels the MMPAD data have higher S/N than equal area data from the CCD (‘cut’). These results show photon detection with the MMPAD to be of comparable or better quality than with the CCD.

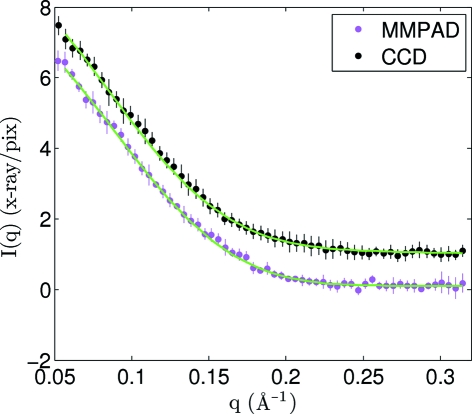
The mean and standard deviations from five measurements of a lysozyme scattering profile acquired with the MMPAD and CCD (‘full-chip’) are shown in Fig. 3 ▶. When the CCD data are scaled to match the data of the MMPAD the standard deviations of the MMPAD measurement are comparable or less than those of the CCD. From q = 0.1–0.3 Å⁻¹ the average of the standard deviations of the MMPAD data are 57% less than those of the CCD data. As seen in Fig. 3 ▶, the standard deviations are relatively independent of q. This is because, while the scattering per pixel drops with increasing q, the total detected photons per q-increment remains approximately constant with q, since the number of pixels covering a q-increment increases as q grows.

Figure 3.

Average scattering profile from lysozyme in solution at a concentration of 5 mg ml⁻¹ acquired with a 100 ms exposure time and attenuation of 11× using the CCD (‘full-chip’) and the PAD. Vertical bars indicate the standard deviation calculated from five scattering profiles acquired using the same sample. Units of X-rays pixel⁻¹ refer to the PAD data. The CCD data and errors are scaled by a factor of 5.2 to match the intensities (which adjusts primarily for the difference in solid-angle per pixel) and then offset by 1 X-ray pixel⁻¹ for easier differentiation. GNOM fits to the data are shown in green.

These scattering profiles (from q = 0.05 Å⁻¹ to q = 0.32 Å⁻¹) were used as inputs to GNOM for evaluation of the radius of gyration (R _g). Table 4 ▶ displays the mean of the radius of gyration measured by both detectors with 11× attenuation and no attenuation acquired with 100 ms exposure time. The table also shows the standard deviation of five measurements (σ_Rg), the average radius of gyration error as returned by GNOM (σ_GNOM) and the average GNOM total estimate metric (TOTAL). The lysozyme radius of gyration is given as 14.3 Å in the literature (Mylonas & Svergun, 2007 ▶). With 11× attenuation the PAD and CCD measured R _g = 14.37 ± 0.59 Å and R _g = 14.26 ± 0.34 Å, respectively. This shows that both detectors, in the described experimental configurations, effectively extracted a common solution SAXS measurement. The large R _g (and higher standard deviation) measured by the MMPAD at no attenuation is hypothesized to be due to radiation-induced aggregation since the value measured increased monotonically with exposure number. In order of exposure number for a single sample where nothing else changed, R _g = 14.24, 14.37, 14.42, 14.59, 14.89 Å. Radiation damage will be discussed further in §3.3.

Table 4. Real-space radius of gyration (R _g) estimates calculated with GNOM from measurements with 100 ms exposure time taken with the MMPAD and the CCD.

σ_Rg is the standard deviation of five measurements of the radius of gyration and σ_GNOM is the mean of the uncertainty returned by GNOM for the five separate measurements. The last column reports the average of the GNOM TOTAL estimate metric (TOTAL) which is a weighted estimate of the criteria that evaluate the quality of the pair-distribution solution found. DISCRP was given zero weight since profile standard deviations were not provided to GNOM as input. A value of 1 is an ideal solution and 0 is unacceptable.

		Rg (Å)	σRg (Å)	σGNOM (Å)	GNOM TOTAL estimate
MMPAD	11× att.	14.37	0.59	0.14	0.96
CCD (full-chip)	11× att.	14.26	0.34	0.16	0.81
CCD (cut)	11× att.	14.16	1.15	0.23	0.87
MMPAD	No att.	14.50	0.25	0.05	0.94
CCD (full-chip)	No att.	14.35	0.11	0.03	0.97
CCD (cut)	No att.	14.36	0.10	0.05	0.98

3.3. Time-resolved demonstration: radiation damage

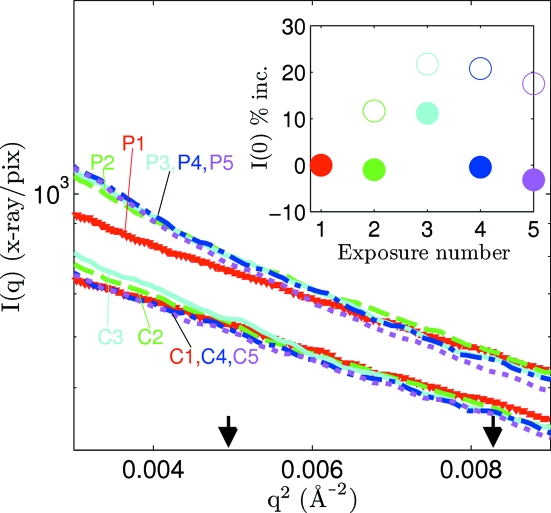
The read-out time (<1 ms) of the MMPAD detector allowed for rapid acquisition of data while the sample evolved without pausing the experiment or closing the X-ray shutter. Fig. 4 ▶ shows multiple Guinier plots of lysozyme acquired with 1 s exposure times taken by both detectors. The dose rate was estimated to be 1.4 × 10⁴ Gy s⁻¹. The five exposures acquired with the MMPAD were taken in rapid succession without closing the X-ray shutter. The time between CCD exposures required detector readout and user intervention during which the X-ray shutter was closed (the intervals between CCD exposures ranged from 35 to 91 s). For the acquisitions with both detectors the sample was irradiated for a total of 5 s. Radiation-induced aggregation is clear in the low-angle regime of the MMPAD curves from exposures two through five. For more quantitative analysis the forward scattering, I(0), was calculated as the intercept in the Guinier region of ln[I(q)] versus q ². In the inset the percent increase of I(0) from the first exposure is plotted versus exposure number for the data from both detectors.

Figure 4.

Low-angle region Guinier plots for 1 s exposures that show the consequence of detector readout time and data acquisition procedures on perceived radiation damage. Acquisitions from the MMPAD are labeled P and from the CCD are labeled C and then both are followed by the exposure number. The Shannon limit (q ² = 0.0049 Å⁻²) and the Guinier limit (q ² = 0.0083 Å⁻²) are indicated by arrows. The inset shows the percent increase in the forward scattering from the first exposure. In the inset, CCD data are represented by filled symbols and MMPAD data by open symbols. There was 860 µs between each exposure acquired by the MMPAD. For the CCD acquisitions the time with the X-ray shutter closed between exposures was, in order, 52, 35, 89 and 91 s.

Radiation damage is not as clear from the sequence of curves acquired using the CCD. This does not mean the CCD data are free from radiation damage effects. Aggregation may have occurred during each exposure acquired with the CCD and corrupted the data, yet during the time between each exposure aggregates may have diffused out of the X-ray spot so that consistency between subsequent curves was maintained. The diffusion constant of lysozyme has been reported as D = 10.6 × 10⁻⁷ cm² s⁻¹ for similar solution conditions (Dubin et al., 1971 ▶) which gives a diffusion length that approximately matches the X-ray spot size in 100 s. This is consistent with the results of Fig. 4 ▶ that diffusion of aggregates may have been significant for data captured at intervals that exceeded 35 s with the CCD detector but not for data acquired at intervals of 860 µs with the MMPAD.

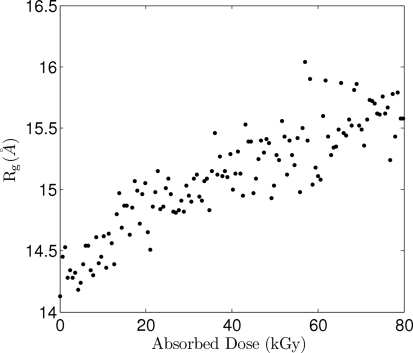
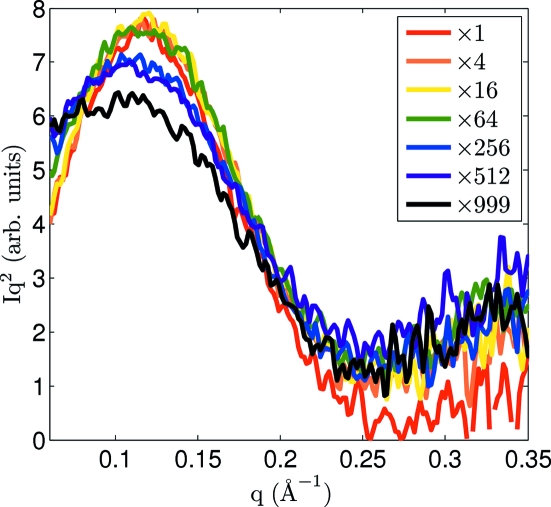
In a separate set of experiments, 25 mg ml⁻¹ lysozyme maintained at 277 K by a water-chilled copper holder (Hong & Hao, 2009 ▶) was studied with the MMPAD at a sample-to-detector distance of 216 mm. The X-ray shutter was opened and the MMPAD continuously captured images with 100 ms exposure time to monitor sample radiation damage (1000 frames were acquired in approximately 100 s). The 100 ms exposure time in this study was set by the intensity of the scatter from the sample, not by the MMPAD. Fig. 5 ▶ shows the radius of gyration as radiation damage accumulates. During the first second R _g increased to 14.5 Å after an estimated dose of 6 × 10³ Gy. After 20 s the radius of gyration increased to 16 Å. Fig. 6 ▶ shows Kratky representations of the scattering at seven levels of dose. At larger accumulated dose the peak in the Kratky plot, centered at 0.12 Å⁻¹ for undamaged samples, flattened and shifted to lower q as the particle size became larger and less well defined. These results show successful capture of time-resolved solution SAXS data with the MMPAD and display the utility of continuous monitoring of sample evolution. The kinetics of radiation damage in solution could be systematically studied with the MMPAD by varying, for example, sample concentration, temperature, amount of cryoprotectants and dose rate.

Figure 5.

Evolution of the radius of gyration from MMPAD measurements during continuous dosing. Each point is from a 100 ms exposure with 860 µs between points with an estimated dose rate of 600 Gy per 100 ms.

Figure 6.

Kratky representation of lysozyme scattering profiles from 100 ms exposures as dose accumulated. In this experiment 1000 frames were acquired in approximately 100 s. The total accumulated dose level at the exposure end is given by 600 Gy multiplied by the factor indicated in the legend.

4. Discussions

4.1. q resolution

The q resolution of SAXS experiments is limited by the beam size at the sample, the beam divergence and energy bandpass, and the detector spatial resolution. As presented by Pedersen et al. (1990 ▶) and Paris et al. (2007 ▶), the q-independent component of the q resolution, W ₀, may be approximated as

where α is the beam divergence, σ_P = P/12^1/2 is the detector spatial resolution (P is the MMPAD pixel-size), σ_B = B/12^1/2 with B the beam size, and d is the sample-to-detector distance. The horizontal beam divergence was estimated to be 0.15 mrad (FWHM) and the beam size at the sample was estimated at 350 µm. With the MMPAD at a distance of d = 350 mm the q resolution is estimated to be W ₀ = 0.0015 Å⁻¹ (RMS). The beam size is the largest contributor to the instrumental broadening in the calculation above. The detector pixel size indicates that q resolution would improve by a reduction of beam size down to 150 µm.

Time-resolved experiments often utilize a broad X-ray energy bandpass for more flux. The energy spread reduces the q resolution linearly with q (Paris et al., 2007 ▶),

For our experiments the broadening owing to energy bandpass is equal to the q-independent broadening in equation (2) at q = 0.24 Å⁻¹. Improvement in the q resolution by adjustment of the contributors to q-independent broadening, W ₀, will be limited by the energy bandpass of the beamline.

Degradation owing to sample radiation damage would be reduced (per incident X-ray photon) by a large beam at the sample with q resolution maintained by a large sample-to-detector distance and low beam divergence. However, the angular extent subtended per pixel would reduce the signal-to-noise ratio of the captured curve. These long sample-to-detector distances would benefit from a large-area photon-counting device.

4.2. Signal-to-noise ratio and detector distance

In solution SAXS experiments the sample-to-detector distance may be increased until the largest desired scattering angle is incident on the edge of the detector in order to utilize the detector’s full extent. The small area of the MMPAD used in these experiments encouraged consideration of the effect of sample-to-detector distance on the signal-to-noise ratio (SNR) of the captured data in the presence of detector read-noise. Since each pixel of a detector (CCD, image plate or integrating PAD) introduces read-noise to the data, an increase in the number of pixels used to measure the scattering will increase the noise of the measurement. Consider a simple model with noise from only two sources: photon noise (Poisson fluctuations of the incident X-rays) and detector read-noise. The SNR in a given q increment may be written as

where f _ϕ is the fraction of the azimuth covered, N is the total number of photons scattered into the angular increment, P is the number of pixels used to capture the angular increment, and σ_pix is the RMS read-noise of the detector pixel. The read-noise in a q-increment grows with the sample-to-detector distance since the number of pixels that are recorded to cover that angular increment increases with the square of the sample-to-detector distance. However, the number of X-rays within the cone covering the same angular azimuth remains constant when the sample-to-detector distance increases. Therefore, according to equation (4), the SNR is reduced by an increase in the sample-to-detector distance.

4.3. Detector spatial response and photon noise

CCD detectors with fiber-optic coupling of a phosphor screen have spatial resolution limited by spreading of visible light in the phosphor and fiber-optic taper (as discussed earlier the spatial response of the CCD detector tested has a standard deviation of 34 µm). The spatial response of PAD detectors is set by horizontal diffusion of drifting charge in the high-resistivity direct detection layer. The horizontal spread for the detector layer thickness and biasing voltage used in these experiments follows a Gaussian distribution with a standard deviation of 9.3 µm. Spread of signal from a single X-ray among multiple pixels, most significant for the CCD detector, reduces the measured incident photon noise (Moy, 2000 ▶; Barna et al., 1999 ▶). Ponchut et al. (2005 ▶) showed the detective quantum efficiency at medium spatial frequency of a phosphor-based CCD detector to be higher than a photon-counting PAD (Medipix) owing to the PAD’s aliasing of photon noise. The PAD aliased photon noise because the point-spread function of the detector layer is smaller than the pixel pitch. This is also the case for the MMPAD in these experiments. The effect of spatial response on photon noise is illustrated by the improved S/N in Table 3 ▶ of the spatially ‘filtered’ MMPAD data versus the standard MMPAD data. The spatial response of the MMPAD is adjustable by varying the high-voltage bias of the detecting layer (Schuette, 2008 ▶). Since the MMPAD pixel integrates signal, an increase in the spread of signal among pixels is not detrimental to operation. In future work an optimum MMPAD spatial response based upon trade-offs between spatial resolution and noise aliasing could be explored.

4.4. Larger MMPAD area

The scattering contrast between protein and buffer is only 5% of the signal from the protein molecule in a vacuum (Das & Doniach, 2006 ▶). This means that many X-rays are required for a reasonable scattering profile such that the accuracy of solution SAXS curves is predominately limited by photon noise. As shown by the simple model of equation (4), capture of the entire azimuth would maximize the signal-to-noise ratio for a given dose to the sample. The experimental configuration used in the described measurements centered the direct beam at a corner of the MMPAD chip. This configuration sacrificed ∼75% of the scattered signal to measure out to scattering angles corresponding to q = 0.32 Å⁻¹. Plans for a larger-area MMPAD constructed from four copies of the chip used here tiled into a 2 × 2 arrangement for an array of 256 × 256 pixels are being developed. Each readout chip has its own output signals such that tiling multiple readout chips to increase area coverage will not increase the readout time, as long as the data storage of the support electronics is sufficiently fast. A 256 × 256 pixel MMPAD would facilitate experiments with the scattered cone centered on the detector to capture the entire azimuth.

Lysozyme is a small protein (14.7 kDa, maximum diameter of 45 Å). The beamline and detector configuration used measured intensities at a minimum of q = 0.05 Å⁻¹ and so, based on Shannon sampling, is not suited for proteins with a maximum diameter larger than 63 Å (some measurements at q lower than the Shannon limit are often desired so the particle size constraint is a high estimate). A detector built as a mosaic of multiple MMPAD chips will allow for studies of larger particles by an increase in the detector-to-sample distance. Experiments on larger particles may particularly benefit from the wide dynamic range, which exceeds 2 × 10⁷, and sub-pixel point-spread function of the MMPAD. The forward scattering depends strongly on particle size, I(0) R ⁶ (Svergun & Koch, 2003 ▶), and the scattering intensity rate of fall with q goes as R ⁴ (Porod approximation of scattering from spheres); as particle size increases, a wider range of scattering intensities and a larger flux-rate near the beamstop is produced. The MMPAD could capture statistically significant data in the wide-angle regime of a combined SAXS and wide-angle X-ray scattering experiment on larger proteins or viruses without saturation in the small-angle regime.

5. Conclusions

Solution SAXS curves can be highly oversampled by the detector. Small detectors at short distances should be able to measure a solution SAXS intensity curve with sufficient resolution. We have shown this by the acquisition of reasonable data with a small detector (19.2 mm × 19.2 mm). Furthermore, in the presence of detector read-noise, a large angular extent per pixel benefits the signal-to-noise ratio.

The MMPAD detector features a large dynamic range and a read-out time of less than 1 ms. The MMPAD was compared with a detector that couples a phosphor screen to a CCD with a fiber-optic demagnifying taper. Detector read-noise was evaluated using methods relevant to solution SAXS. Read-noise measurements normalized to pixel area were an average of 3.0 times better for the MMPAD. Protein scattering profiles were acquired with both detectors and assessed using GNOM fits to the data, which showed the MMPAD to capture scattering profiles of similar or better quality than the CCD.

The MMPAD read-out time of less than 1 ms allowed continuous tracking of sample evolution as radiation damage accumulated and showed the sample radius of gyration to increase continuously with dose. Measurements of lysozyme at concentrations of 5 mg ml⁻¹ produced meaningful data with 100 ms exposure times and 11× attenuation. These results suggest that the MMPAD at CHESS G1 station could be used to continuously capture solution SAXS data with 10 ms exposure times for time-resolved investigations of an evolving sample. An even more ideal situation would be to use four MMPAD chips to cover a wider area.