Figure 5.

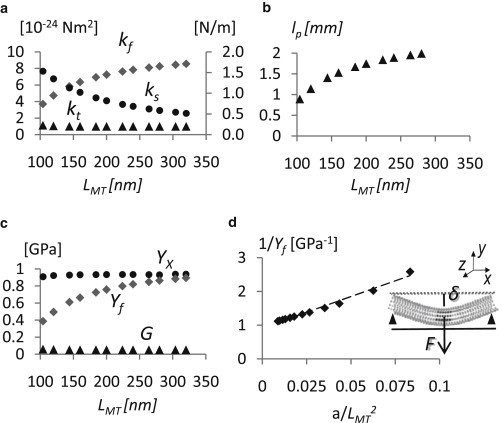
(a) Data showing the relationship among the bending stiffness k_f (diamonds), stretching stiffness k_s (circles), torsion stiffness k_t (triangles), and the MT length, L_MT. The values k_t remain constant with respect to L_MT, while k_f increases and k_s decreases when MT length rises. (b) Relation between the persistence length l_p (triangles) and L_MT. A strong dependence of l_p on the MT length is noticeable. (c) Bending modulus Y_f (diamonds), stretching modulus Y_x (circles), and shear modulus G (triangles), directly obtained by torsion stiffness versus L_MT. The Y_f values markedly increase with the MT length, approaching the value of Y_x (∼1 GPa) for L_MT at ∼300 nm. The G-value is constant and roughly equal to 0.05 GPa, i.e., two-orders-of-magnitude less than the Young's modulus Y_x. (d) Inverse of the bending modulus 1/Y_f, with respect to the constant a/L_MT², where a is equal to 12f(I/A) and f is a geometric factor equal to 1.38 in case of a hollow cylinder. The linear regression gives directly the value of Y_x as the inverse of the y intercept of the fitting curve (Y_x = 1.1 GPa), while G is the inverse of the slope of the curve (G = 0.05 GPa). A graphical description of the MT bending test is also reported; the MT is supported at the free ends and deflected, δ, by a concentrated force, F, acting in the middle.