Lateral Dynamics of Proteins with Polybasic Domain on Anionic Membranes: A Dynamic Monte-Carlo Study

Abstract

Positively charged polybasic domains are essential for recruiting multiple signaling proteins, such as Ras GTPases and Src kinase, to the negatively charged cellular membranes. Much less, however, is known about the influence of electrostatic interactions on the lateral dynamics of these proteins. We developed a dynamic Monte-Carlo automaton that faithfully simulates lateral diffusion of the adsorbed positively charged oligopeptides as well as the dynamics of mono- (phosphatidylserine) and polyvalent (PIP₂) anionic lipids within the bilayer. In agreement with earlier results, our simulations reveal lipid demixing that leads to the formation of a lipid shell associated with the peptide. The computed association times and average numbers of bound lipids demonstrate that tetravalent PIP₂ interacts with the peptide much more strongly than monovalent lipid. On the spatially homogeneous membrane, the lipid shell affects the behavior of the peptide only by weakly reducing its lateral mobility. However, spatially heterogeneous distributions of monovalent lipids are found to produce peptide drift, the velocity of which is determined by the total charge of the peptide-lipid complex. We hypothesize that this predicted phenomenon may affect the spatial distribution of proteins with polybasic domains in the context of cell-signaling events that alter the local density of monovalent anionic lipids.

Introduction

Electrostatic forces play a crucial role in the interaction of proteins with biological membranes. Although the extracellular leaflet of the cellular plasma membrane is primarily neutral, the inner cytoplasmic leaflet and endomembranes contain 20–40% of anionic lipids (1) and reversibly associate with a large number of proteins by means of electrostatic interactions (2–5). Remarkably, several highly important signaling proteins, such as Ras small GTPases, phosphatase PTEN, and nonreceptor tyrosine kinase Src, as well as actin regulators WASP and MARCKS, bind to the membranes using intrinsically unstructured stretches of positively charged residues, known as polybasic stretches or domains (6–10). Although the membrane-recruitment role of these domains has been studied extensively (8,11,12), few studies have explored how their nonspecific interaction with negatively charged lipids affects the lateral mobility of the entire proteins and their spatial localization within recently characterized nanoclusters (13,14) and microdomains (15,16).

The lateral dynamics of proteins and lipids within biological membranes has long captured the interest of researchers in multiple disciplines (17–19). The development of biophysical techniques such as fluorescence recovery after photobleaching and fluorescence correlation spectroscopy (20) enabled extensive exploration of diffusive properties of lipids and proteins in various experimental systems. The introduction of artificial membranes, such as supported phospholipid bilayers (21), provided a convenient and well-controlled in vitro model, whereas the extracellular leaflet of the plasma membrane, which is accessible to fluorescently labeled antibodies, became the in vivo system of choice (22). These analyses demonstrated that the lateral mobility of transmembrane proteins is typically 1–2 orders of magnitude lower than that of lipids, whereas peripheral membrane proteins, such as GPI-anchored proteins and lipid-specific antibodies, diffuse 2–8 times more slowly than lipids (22–24). An in vitro study of annexin IV adsorbed to the surface of a phosphatidylcholine (PC)/phosphatidylglycerol (PG) bilayer suggested that electrostatic interaction between proteins and lipids is an important determinant of lipid lateral mobility (25). McLaughlin and colleagues (26) measured the diffusion coefficient of phosphatidylinositol 4,5-bisphosphate (PIP₂), a biologically important lipid that is expected to interact strongly with proteins due to its highly negative charge (−4), and found that it diffuses 3–4 times more slowly ($D=0.8\pm 0.2\mu {\text{m}}^2/\text{s}$) on the inner leaflet of fibroblasts and epithelial cells than within cellular blebs and artificial phospholipid membranes ($D=2.5-3.3\mu {\text{m}}^2/\text{s}$). This finding is in agreement with other results obtained for both PIP₂ and PIP₃ (27,28).

Considerably less is known about the influence of varying concentrations of negatively charged lipids on the lateral dynamics of proteins with polybasic domains. An in vitro analysis by Golebiewska et al. (29) demonstrated that Lys-13, a peptide that mimics the polybasic domain of MARCKS, diffuses more slowly on giant unilamellar vesicles containing 1% of PIP₂ than on vesicles consisting only of neutral PC and monovalent phosphatidylserine (PS; −1). The development of fluorescent protein techniques has allowed investigators to access the in vivo dynamics of proteins on the inner leaflet of the plasma membrane. The results from such analyses demonstrated that under physiological conditions (20–40% of monovalent lipids and <1% of PIP₂), the diffusion coefficients of proteins attached by a lipid modification and a polybasic domain are similar to those of other peripheral membrane proteins (4). Thus, Henis and colleagues (30) inferred $D=0.57\mu {\text{m}}^2/\text{s}$ for the inactive (tightly folded) conformation of Src. Other members of the Src family, which are devoid of the polybasic domain but possess multiple lipid moieties, were found to have similar mobilities: $0.1-0.6\mu {\text{m}}^2/\text{s}$ for dually acylated Lyn (31–34) and $0.26\mu {\text{m}}^2/\text{s}$ for triply lipidated Lck (35). Analogously, the small GTPase KRas, which has a pronounced polybasic domain (+7), was found to diffuse with a mobility of $0.2-0.35\mu {\text{m}}^2/\text{s}$(31,34,36). This value is close to that of HRas ($0.35-0.5\mu {\text{m}}^2/\text{s}$) (36), which has triple lipid modification but no polybasic domain. Another study revealed that KRas diffuses as rapidly as HRas and NRas, and nearly as rapidly as fluorescent lipid probes (37). Comparable in vivo diffusion coefficients were also recently reported for proteins with Pleckstrin homology domains that interact with individual phosphoinositide lipids (5). These observations are remarkable in the light of results indicating that polybasic domains and cationic oligopeptides (e.g., polylysine) efficiently sequester anionic lipids, particularly those with a large charge valence (i.e., PIP₂ and PIP₃) (9,38). Indeed, the in vivo diffusion coefficients of Src and KRas suggest that the formation of such electronegative shells does not appreciably retard the lateral mobility of proteins with polybasic domains, at least under physiological conditions.

Computational modeling has played a considerable role to characterize various aspects of protein diffusion on biological membranes (39–42). Electrostatic interactions between lipids and proteins have also received significant theoretical attention. However, as in the experimental studies, most of these investigations have focused on the adsorption-desorption dynamics of proteins and the associated demixing of negatively charged lipids (3,7,9,29,38,43–52), leaving the lateral dynamics of adsorbed proteins largely unexplored. Hinderliter et al. (53) performed Monte-Carlo simulations of multiple proteins on a lattice and, in addition to adsorption and desorption, introduced protein diffusion. However, they did not consider in detail how the electrostatic interactions of proteins with underlying lipids contribute to the protein lateral dynamics. Recently, Khelashvili et al. (54) developed a hybrid mean-field approach in which the lateral dynamics of a single polylysine peptide and the surrounding lipid is simulated by alternating random peptide movements and lipid relaxation in accordance with the Cahn-Hillard equation. Due to the absence of explicit thermal fluctuations in the lipid subsystem, lipids do not possess lateral dynamics independently of that of the peptide.

In this work, we developed a dynamic Monte-Carlo model on a hexagonal lattice representing a lipid membrane with single lipid resolution. The lateral dynamics of a positively charged peptide mimicking the polybasic domain of a protein is considered on an overlying lattice. All lipids and peptide(s) undergo independent thermal motion, and the energy of their interaction is computed according to the screened Coulomb potential. We restrict the spatial domain of interest to $L\le 200\text{n}\text{m}$ and the observation time to ${\tau }_O\le 0.01\text{s}$. Given the chosen space and timescales, numerical simulation of the constructed automaton is computationally feasible even at the selected high level of molecular detail. We focus our attention on the proteins bound to the membrane by a single lipid modification and a polybasic domain. Because for this class of proteins the characteristic time of association with the membrane is on the order of seconds ($\tau \ge 1\text{s}\gg {\tau }_O$ (4)), in our model we assume that the peptide remains bound to the lipid bilayer throughout the entire simulation.

Model

To simulate the dynamics of positively charged oligopeptides on the surface of a membrane, we developed a dynamic Monte-Carlo automaton consisting of two parallel hexagonal lattices. Assuming that the average area per lipid is $\sim 0.6\text{n}{\text{m}}^2$ (55), we chose the spatial period of the lipid lattice to be 0.8 nm (Fig. 1 A). The lattice is populated by three types of lipids: 1), neutral (e.g., PC or PE); 2), monovalent negatively charged (−1, which for convenience is hereafter referred to as PS); and 3), PIP₂ with charge −4. Because the focus of this study is on electrostatic interactions mediated by the lipid headgroups, the precise nature of lipid aliphatic tails is left unspecified.

Figure 1.

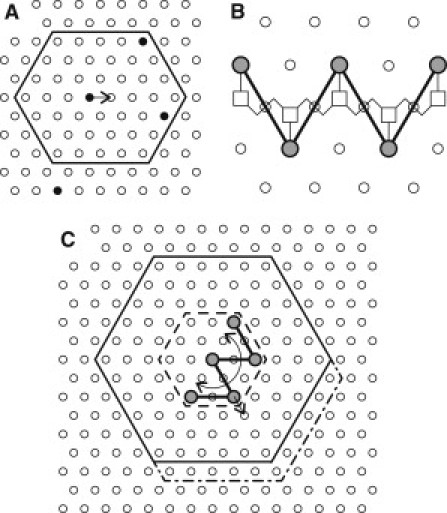
Model definition. (A) Lipid lattice. The neighborhood used to calculate the lipid movement $\Delta E$ is indicated by the solid line. Charged lipids are shown as solid circles. (B) Projection of Lys-5 peptide backbone on the lipid lattice. α-Carbons are denoted by open squares, and positively charged side chains are indicated by solid circles. (C) Peptide lattice with W-shaped peptide structure. Energy neighborhoods for translational and rotational moves are shown by dash-dotted and solid lines, respectively. Lipids enclosed within the hexagon shown by the dashed line rotate together with the peptide.

We chose pentalysine (Lys-5, +5) as the oligopeptide mimicking a typical polybasic domain of a protein. According to previously reported linear dimensions (49), the backbone of this peptide can be projected with minimal deformations onto the chosen lipid lattice so that the positively charged lysine side chains approximately overlie alternate lipid nodes, as shown in Fig. 1 B. Using this geometric approximation, we represent Lys-5 in our model by a rigid W-shaped ball-and-stick structure that occupies discrete nodes on the peptide hexagonal lattice that lies above the lipid lattice and is geometrically identical to it (Fig. 1, B and C). On the basis of previous studies (46,56), we chose $d=0.28\text{n}\text{m}$, an approximate diameter of a water molecule, as the distance between the two parallel lattices to achieve an optimal balance between the Coulombic attraction and desolvation penalties.

We assume that peptide amino acid residues and lipid headgroups are point charges that interact electrostatically according to the screened Coulomb potential (also known as the Yukawa potential):

$$V\left(\overrightarrow{r}\right)=\frac{q_1{q}_2}{4\pi \varepsilon {\varepsilon }_0}\frac{e^{-r/\lambda }}{r}$$ (1)

where λ is the Debye length and $\varepsilon =80$ is a dielectric constant of water. For colloidal dispersions and electrolytes, the Debye length

$$\lambda =\sqrt{\frac{\varepsilon {\varepsilon }_0{k}_{B}T}{2N_A{e}^{2}I}}$$ (2)

is a function of temperature T and the ionic strength of the solution I. Following a commonly used approximation of the cytoplasm as a 0.1 M solution of a monovalent salt, we adopted $\lambda =1\text{n}\text{m}$ as the standard, physiologically relevant Debye length for the majority of our simulations. With the chosen parameters, the energy of the electrostatic repulsion between the two neighboring PS lipids is $\sim 0.4k_{B}T$, whereas that of the attraction between a peptide node and directly underlying it PS lipid is $-1.9k_{B}T$ ($-7.6k_{B}T$ for the interaction with PIP₂).

Lipids undergo continuous thermal motion that is represented in the automaton by the standard Kawasaki moves (57,58), whereby the position of a lipid is swapped with that of one of its six neighbors, chosen at random. As required by the Metropolis algorithm, the energy cost of the movement, $\Delta E$, is computed using the pairwise interactions of all charges lying within (lipids) and directly above (peptide nodes) the hexagonal neighborhood shown in Fig. 1 A. The size of the neighborhood is chosen empirically to ensure that charges lying outside of the neighborhood cumulatively contribute <5% of the total $\Delta E$ computed over the entire lattice (this is equivalent to cutting off the potential in Eq. 1 above ∼3 Debye lengths).

Peptides undergo both translational and rotational movements. A translational movement is defined as a shift of the entire peptide by one lattice period along one of the six directions chosen at random. Of importance, if the lateral mobility of the peptide is lower than that of the freely moving lipids, which is typically the case (at least in vivo; see Introduction), the lipids will undergo rapid demixing that results in significant accumulation of negative charge directly underneath the peptide. For Lys-5 as a probe peptide and a physiologically relevant 25% mole fraction of PS (75% neutral lipid) on the lipid lattice, there are on average four PS lipids directly underneath the five peptide nodes (see Results and Discussion for details). An attempt to move the peptide away from this negatively charged lipid cluster would result in an energetic penalty of ∼$+7k_{B}T$, and thus would be accepted with the probability $P=\exp \left(-\Delta E/k_{B}T\right)\approx {10}^{-3}$, resulting in effective immobilization of the peptide. In the presence of multivalent anionic lipids (e.g., PIP₂), the situation would be even worse. The resulting stalemate in the peptide lateral dynamics was previously described in detail (54). In the broader context of dynamic Monte-Carlo methods, it is known that this kinetic trapping phenomenon is caused by strong, short-range interactions of particles. To overcome this phenomenon, Whitelam and Geissler (59) suggested the use of collective moves involving whole clusters of strongly interacting particles. As applied to the system at hand, the most natural implementation of this idea would be to move the peptide together with the strongly bound lipids. Thus, to avoid the otherwise inevitable kinetic trapping of the peptide, each proposed translational movement of the peptide is accompanied by a swap of lipids that directly underlie the peptide nodes. The energy cost of the resulting collective movement is then computed within a neighborhood asymmetrically extended in the direction of the proposed movement (dot-dashed line in Fig. 1 C) as defined above for the lipid movement.

Given the restriction of the peptide dynamics to the discrete lattice with hexagonal geometry, we chose the central peptide node as the best approximation for the peptide center of mass around which it undergoes rotation by quantal increments of ±60°, with the sign chosen at random (Fig. 1 C). Again, to avoid kinetic trapping, the peptide is rotated together with all lipids enclosed in a hexagonal envelope centered at the peptide center of mass (dashed line in Fig. 1 C). The energy cost of the resulting movement is computed within the symmetrical hexagonal neighborhood indicated in Fig. 1 C by the solid line. The rotational movement, as defined above, is not likely to faithfully represent the true rotational dynamics of the peptide. Instead, within the scope of this study, it serves primarily to ensure isotropy of the peptide lateral dynamics (see Supporting Material).

One complete time step of the automaton evolution consists of the following consecutive operations: 1), all charged lipids on the lipid lattice, including those directly underneath the peptide(s), attempt to move as defined; 2), the peptide tries to perform a translational movement; and 3), the peptide attempts a rotational movement. In the case of multiple peptides, steps 2 and 3 are repeated for each peptide on the peptide lattice. Translational moves resulting in the overlap of the confounding envelopes of any two peptides are rejected. Further information regarding the validation, calibration, and simulation details of our automaton is provided in the Supporting Material.

It is important to point out some limitations of our modeling approach. First, our automaton is a kinetic Monte-Carlo model; therefore, it neglects possible hydrodynamic effects beyond the viscous drag, which we account for by scaling the automaton using the experimentally measured diffusion coefficients of lipids and proteins (see Supporting Material). Second, although the screened Coulomb potential is generally well accepted in the literature (44,45), it could be further improved upon by the use of a more detailed Poisson-Boltzmann approach. However, this additional complexity would make it more challenging to introduce the thermal noise that drives the peptide and lipid diffusion. Ultimately, one might wish to use either a multiscale or an all-atom molecular-dynamics approach. However, all of these methods would lead to greatly increased computational costs and prevent us from attaining the space and timescales necessary to detect the phenomena described below. Furthermore, we expect that these more-detailed approaches would not qualitatively alter our results and conclusions.

Results and Discussion

Lipid sequestration and demixing

First, we set out to explore the interaction of protein polybasic domains represented in our model by Lys-5 oligopeptide with mono- and polyvalent anionic lipids. Because of the geometric approximation used in the design of our Monte-Carlo automaton (see Model section), the lipid lattice nodes positioned directly underneath the five peptide nodes have a preferential location as being the closest to and thus the most strongly interacting with the peptide positive charges. Fig. 2 A shows the steady-state probability of these nodes being occupied by PS lipids at various molar fractions of PS. In the physiological range of PS concentrations (15–25%), the positive charge of the peptide is only partially (∼50%) compensated for by lipid molecules. Due to the monovalent nature of the lipid, even at the unrealistically high PS concentrations, the total charge of the peptide together with that of the associated lipids remains positive. This situation changes dramatically in the presence of polyvalent PIP₂ (Fig. 2, B–D). At a seemingly negligible fraction of 0.5%, on average three molecules of PIP₂ are predicted to be in direct association with the peptide. This brings the total charge of the peptide-lipid complex to −7. As expected, polyvalent PIP₂ effectively competes with PS for binding to the peptide, and at concentrations >0.5% it practically displaces monovalent lipids from the peptide (see Fig. 2 C). We also computed the average numbers of both mono- and polyvalent lipids associated with Lys-6 and Lys-7 under the same assumptions about their membrane-bound conformation as for Lys-5. We found that, per peptide residue, these values were almost identical and equal to those of Lys-5. This suggests that for the considered membrane-bound conformation of the peptide, individual lysine residues interact with anionic lipids essentially independently of each other, and thus the above results can be readily extrapolated to polybasic domains with variable length.

Figure 2.

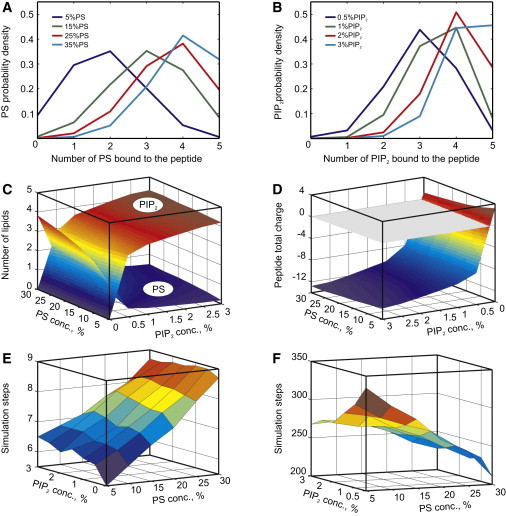
Interaction of the peptide with lipids. (A and B) Probability density functions of lipid association for PS and PIP₂, respectively. For all plots in B, the PS fraction is 25%. (C) Average numbers of PS and PIP₂ molecules associated with the peptide at varying lipid concentrations. (D) Charge of the peptide together with associated lipids. (E and F) Average peptide association times for PS and PIP₂, respectively.

A comparison of the average peptide-lipid association times shown in Fig. 2, E and F, reveals further differences between the interactions of mono- and polyvalent lipids with the peptide. In our simulations, a molecule of PS spends only 5–10 time steps ($\sim 1-2\mu \text{s}$ assuming $D_L=1\mu {\text{m}}^2/\text{s}$) in direct association with the peptide before resuming its free diffusion. In contrast, association of PIP₂ with the peptide is 30–50 times longer, which implies that the peptide and lipid diffuse together, as was also suggested by the experimental results of Golebiewska et al. (29). To further characterize the extent of lipid demixing caused by the adsorbed peptide, we calculated the lipid probability distribution in a square neighborhood moving together with the peptide as shown in Fig. 3, A and B. As expected, in the absence of PIP₂, the monovalent lipids also exhibit increased density between and around the five peptide nodes; however, due to the Debye screening, this effect does not extend beyond one lipid node away from the peptide. Note also that the peptide-induced demixing saturates, and an increase in the PS concentration beyond 25% does not cause a detectable difference in the lipid probability density.

Figure 3.

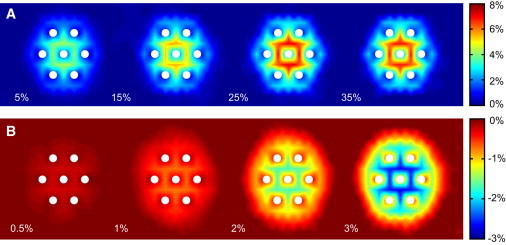
Lipid demixing caused by the peptide. Pseudocolor represents deviation of the local concentration of PS (A) and PIP₂ (B) from the expected average values indicated in the figure. (A) PIP₂ concentration is 0%. (B) PS concentration is 25%. To produce a smooth concentration field, the true values were projected from the sparse hexagonal lipid lattice onto a fine square grid and intermediate values were computed by spline interpolation. Large values corresponding to the lipid positions located directly underneath the peptide nodes (solid circles) have been removed to reveal subtle details.

A reverse distribution of lipid density is seen in the presence of PIP₂. Since the lipid lattice positions directly underlying the peptide nodes have a high probability of being occupied by PIP₂ (cf. Fig. 2 B), negatively charged lipids in the nearby nodes experience strong repulsion that by far outweighs attraction to the peptide. The resulting depletion is particularly prominent in the distribution of PIP₂. In fact, free PIP₂ molecules are almost never found between the peptide nodes (see Fig. 3 B). A similar (albeit relatively less dramatic) depletion effect is also seen in the distribution of PS molecules around the peptide complexed with multiple PIP₂ lipids.

Although our results indicate that all negatively charged lipids undergo demixing, the relative effects of this phenomenon on the spatial distribution of mono- and polyvalent lipids are entirely different. This can be readily seen from the relative lipid enrichment calculated as the ratio of the actual number of lipids found in the area of the membrane perturbed by the peptide to the number of lipids expected within the same area in the absence of the peptide. Using a hexagonal neighborhood with 37 lipid nodes and the data presented in Fig. 3, we find that, at the average concentration of 1%, PIP₂ is enriched by ∼10-fold, whereas PS, at 35%, is enriched only by 1.26. This is in good agreement with previously published experimental results (9,29,38) demonstrating that sequestration of polyvalent PIP₂ by polylysine is highly significant, whereas that of PS is practically negligible.

Diffusion in the spatially homogeneous membrane

We next considered the lateral dynamics in the system where the only spatial heterogeneity is the lipid density perturbation induced by the protein itself. In accord with earlier results (29), for a bilayer consisting of only neutral and monovalent lipids we found no systematic variation of the peptide diffusion coefficient in a broad range of PS concentrations (10–30%; see Fig. 4 A). This is not surprising given that the peptide only weakly perturbs spatial distribution of monovalent lipids in the absence of highly charged phosphatidylinositol polyphosphates. However, a small decrease in the peptide diffusion coefficient from its maximal value $D_0$, observed in the absence of negatively charged lipids, to a reduced value $D^{\prime }\approx 0.86D_0$ was seen between 0% and 10% of PS. A similar weak and likely experimentally undetectable effect was also observed in a previous modeling study (54). We speculate that the slight reduction in peptide mobility found in our model may reflect effective friction associated with the motion of the PS molecules that constitute a loose shell formed around the peptide due to the lipid demixing described above.

Figure 4.

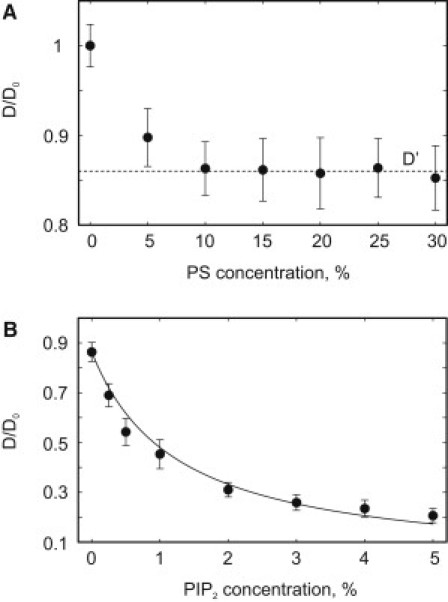
Dependence of the peptide diffusion coefficient on the concentration of PS (A) and PIP₂ (B). All simulations in B were performed with 25% of PS; therefore, at 0% of PIP₂, the peptide diffusion coefficient, $D^{\prime }$, is already < $D_0$.

Fig. 4 B shows that the lateral mobility of the peptide diminishes with an increase in the PIP₂ concentration. This behavior potentially can be explained by several nonmutually exclusive arguments. First, the lateral dynamics of the peptide with the associated PIP₂ molecules can be compared with diffusion of a charged colloid particle in a two-dimensional suspension. Due to the Debye screening, Coulombic repulsion between the negatively charged peptide and freely diffusing PIP₂ molecules becomes a finite-radius interaction that to some extent can be approximated by the hard-sphere potential. Thus, Fig. 4 B also presents a fit of the simulation results to an expression of the form:

$$\frac{D^{\prime }}{1+\alpha \varphi }$$ (3)

where ϕ is the molar fraction of PIP₂, and the viscosity, according to Einstein's formula for dilute solution of hard spheres (60), depends on the particle volume fraction ${\varphi }^{\prime }$ as $\eta =1+{\alpha }^{\prime }{\varphi }^{\prime }$. Here we assume that the effective volume fraction ${\varphi }^{\prime }$ is directly proportional to the molar fraction ϕ. Second, as the concentration of PIP₂ increases, so does the size of the lipid shell around the peptide (see Fig. 3 B). The concomitant increase in the friction associated with diffusion of this shell could also scale according to Eq. 3. Because the results shown in Fig. 4 B were obtained for a single diffusing peptide, any potential effects emerging due to the peptide-peptide interactions may not contribute to the observed reduction in lateral mobility.

Lateral drift in the presence of lipid gradients

Experimental data indicate that various lipid-modifying enzymes can be rapidly recruited and activated on the membrane in localized foci. Lipid kinases, phosphatases, and some phospholipases alter lipid charge by adding or removing phosphate groups. The associated gradient of surface charge can generate a temporary electrostatic potential along the membrane. Polybasic domains positioned immediately above the membrane (49) are natural candidates for perceiving and responding to such potentials. This raises the tantalizing and essentially unexplored possibility that spatial heterogeneities in the distribution of anionic lipids may influence the lateral dynamics of proteins with polybasic domains, at least on short timescales.

In support of this hypothesis, we first consider a continuous distribution of charged lipids described by a density field $\rho \left(\overrightarrow{r}\right)$ and assume that within a certain finite domain with characteristic size $L_d\gg l_p$ (where $l_p$ is the size of the peptide), $\rho \left(\overrightarrow{r}\right)$ on average has a constant gradient. The peptide located at ${\overrightarrow{r}}^{\ast }$ within this domain interacts with charged lipids according to Eq. 1. The total interaction potential between the peptide and all of the membrane lipids can be described as:

$$V\left({\overrightarrow{r}}^{\ast }\right)\simeq \int d\overrightarrow{r}\frac{Zq}{4\pi \varepsilon {}_0\varepsilon }\rho \left({\overrightarrow{r}}^{\ast }+\overrightarrow{r}\right)\frac{e^{-r/\lambda }}{r}$$ (4)

where we have approximated the sum over all discrete lipid locations with an integral over the surface. For simplicity, we assume that all lipids have the same charge q. The peptide will generally experience a force that is equal to the minus gradient of this potential:

$$\overrightarrow{f}\left({\overrightarrow{r}}^{\ast }\right)=-\frac{\partial V\left({\overrightarrow{r}}^{\ast }\right)}{\partial {\overrightarrow{r}}^{\ast }}=-\frac{Zq}{4\pi \varepsilon {}_0\varepsilon }\int d\overrightarrow{r}\overrightarrow{\nabla }\rho \left({\overrightarrow{r}}^{ \ast }+\overrightarrow{r}\right)\frac{e^{-r/\lambda }}{r}$$ (5)

Integration of Eq. 5 can be explicitly performed analytically if the gradient does not depend on $\overrightarrow{r}$, i.e., if $\overrightarrow{\nabla }\rho \left({\overrightarrow{r}}^{\ast }+\overrightarrow{r}\right)\equiv \overrightarrow{\nabla }\rho \left({\overrightarrow{r}}^{\ast }\right)$. This assumption does not introduce any appreciable error, because the integrand in Eq. 5 is distinct from zero only in a small neighborhood of ${\overrightarrow{r}}^{\ast }$, which is defined by the finite radius of the Yukawa potential. Transforming to polar coordinates, we obtain:

$$\overrightarrow{f}\left({\overrightarrow{r}}^{\ast }\right)\simeq -\frac{Zq}{4\pi \varepsilon {}_0\varepsilon }\overrightarrow{\nabla }\rho \left({\overrightarrow{r}}^{\ast }\right){\int }_0^{2\pi }d\theta {\int }_0^{\infty }rdr\frac{e^{-r/\lambda }}{r}$$ (6)

Using substitution $r\to r/\lambda$, we can solve the last integral in Eq. 6 to obtain

$$\overrightarrow{f}\left({\overrightarrow{r}}^{\ast }\right)=-\frac{Zq}{2\varepsilon {}_0\varepsilon }\lambda \overrightarrow{\nabla }\rho \left({\overrightarrow{r}}^{\ast }\right)$$ (7)

Finally, using the Stokes-Einstein's relation, we can express the velocity with which the peptide propelled by the force $\overrightarrow{f}$ moves in a viscous medium (membrane):

$$\overrightarrow{v}=\frac{D_p}{k_{B}T}\overrightarrow{f}=-\frac{Zq}{2\varepsilon {}_0\varepsilon }\frac{\lambda D_p\overrightarrow{\nabla }\rho \left({\overrightarrow{r}}^{\ast }\right)}{k_{B}T}$$ (8)

This velocity can be also expressed through the Bjerrum length $l_B=e^2/\left(4\pi {\varepsilon }_0\varepsilon k_{B}T\right)$, which represents the distance at which two elementary charges interact with the energy equal to thermal:

$$\overrightarrow{v}=-2\pi \frac{Zq}{e^2}{l}_B\lambda D_p\overrightarrow{\nabla }\rho \left({\overrightarrow{r}}^{\ast }\right)$$ (9)

Thus, neglecting lipid density fluctuations, this simplified theoretical ansatz argues that a charged peptide will experience a drift along the gradient of lipid concentration field with velocity $\overrightarrow{v}$ proportional to the peptide charge Z, its diffusion coefficient $D_p$, Debye length λ, and the magnitude of the lipid gradient. Following the approach developed by Tzlil et al. (44), we also analyzed the effect of the membrane hydrophobic core and found that, at least for the predicted drift velocity, this refinement leads to only a minor quantitative correction that is not considered further (see Supporting Material). Note that similar formulas can be derived for diffusiophoretic and electrophoretic velocities in colloidal systems; however, in such systems, one must explicitly consider the solvent hydrodynamics to obtain the quantitatively correct velocity values (61,62).

Until now, we have left the value of the peptide-associated charge, Z, unspecified. Indeed, its definition merits a special consideration. The peptide has the intrinsic positive charge +1 per residue (in total +5 for Lys-5). Sequestration of negatively charged lipids upon adsorption to the membrane results in a complex with a total charge that depends on the lipid composition of the membrane (cf. Fig. 2 D). If the peptide undergoes Brownian motion together with bound lipids, as is assumed in our model, the charge Z should reflect this fact. Moreover, because the motion of the peptide-bound lipids induces displacement of other lipids, as formalized by the Kawasaki movement (see Model), the current associated with the motion of displaced lipids should be also taken into the consideration. For example, consider the dynamics of the peptide on the membrane consisting only of neutral and monovalent lipids (PS). It can be readily seen (see Supporting Material and Fig. S1) that once all translocating charges have been included, the effective moving charge of the peptide node is given by:

$$Z\left(\rho \right)=1-p\left(\rho \right)\left(1-\rho \right).$$ (10)

This function is shown by the solid line in Fig. S1 B in comparison with the simulation data (open circles). Remarkably, Eq. 10 suggests that in a very broad and (incidentally) physiologically relevant range of monovalent lipid concentrations (10–50%), the effective charge of the moving peptide changes very little and equals to $+0.5\pm 0.05$ (per peptide node). This surprising result predicts that as the peptide drifts along the lipid gradient, its effective charge Z will change very little and thus the drift velocity will remain approximately constant.

Using Eq. 10 as the definition of the effective charge, we set out to test the predictions of the mean-field ansatz (Eq. 8) simulating the dynamics of the peptide positioned in a constant gradient of a monovalent lipid. To that end, we generated stationary lipid distributions with variable constant gradient (linear slopes) as described in the Supporting Material. We also varied the peptide diffusion coefficient $D_p$ and Debye length λ. The results of these simulations averaged over several thousands of individual stochastic realizations are presented in Fig. 5, A–C. They show that, in good agreement with Eqs. 8 and 10, the peptide drifts in the direction of the lipid gradient with a velocity that is approximately proportional to $D_p$, λ, and $\overrightarrow{\nabla }\rho \left({\overrightarrow{r}}^{\ast }\right)$. Of interest, we found that, to achieve the best fit between Eq. 8 and the simulation data, an empirical prefactor $\vartheta =0.353$, identified with the least mean-square method, was required. We speculate that this velocity reduction could be caused by the effective friction force associated with the motion of the lipid shell (see Supporting Material for details). Although in the automaton simulations the peptide exhibited only a fraction (∼30%) of the velocity predicted by Eq. 8, the absolute magnitude of the observed drift velocity is fairly significant. For example, at $D_p=0.17D_0$ ($D_0=1\mu {\text{m}}^2/\text{s}$), Debye length $\lambda =1\text{n}\text{m}$, and the gradient 0.3%/nm, the expected velocity value is ∼$3\mu \text{m}/\text{s}$.

Figure 5.

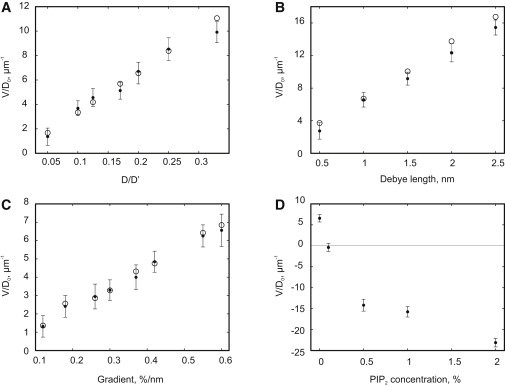
Dependence of the peptide velocity on the peptide diffusion coefficient (A), Debye length (B), magnitude of the lipid gradient (C), and total charge (D). Simulation results (solid circles) are compared with the values predicted by Eq. 8 (open circles). In A, $D^{\prime }$ is as defined in Fig. 4A and in the text. When not otherwise shown in the figure, the peptide diffusion coefficient is $0.2D_0$ and the lipid gradient is $0.6\%/\text{n}\text{m}$.

As would be expected from the sparse nature of the spatial distribution of PIP₂ at physiologically meaningful concentrations, shallow gradients of PIP₂ (e.g., from 3% to 0% over 100 nm) superimposed on the homogeneous distribution of monovalent lipids produced no detectable effect on the peptide lateral dynamics. However, addition of PIP₂ to the gradient of a monovalent lipid, even at small concentration, alters the lateral dynamics of the peptide dramatically. In the example shown in Fig. 5 D, at 0% of PIP₂, the peptide robustly ascends the gradient. However, already at ∼0.1% PIP₂, the peptide has become effectively electroneutral and shows no systematic drift in either direction. With a further increase in the PIP₂ concentration, the peptide moves rapidly down the gradient with a velocity proportional to the total charge of its complex with bound negative lipids (cf. Fig. 2 D). Thus, addition of PIP₂ switches the attractive effect of a gradient of monovalent lipid to strongly repulsive. Furthermore, as shown in Fig. 2, C and D, in the physiologically relevant PIP₂ range (0–1%), the number of molecules of PIP₂ that are bound to the peptide and, consequently, the sequestered charge change very steeply with the average PIP₂ concentration. Therefore, even a small change in the total membrane PIP₂ content, e.g., due to signal-induced production or degradation, could drastically alter the microenvironment of proteins with polybasic domains.

Conclusions

The notion that a lipid shell forms as a result of hydrophobic Van der Waals interactions around a transmembrane protein and diffuses laterally together with the protein has been firmly established (see Marsh (63) for review). Previous work (46-54) demonstrated that electrostatic interaction between proteins with polybasic domains and anionic lipids causes lipid demixing and thus should also generate shells. An important unresolved question is whether positively charged proteins diffuse together with electrostatically bound lipids (the nonslip mode) or glide over the bilayer surface without dragging the lipids. The latter mode (dubbed “skating”) was reported for Lys-13 on the surface of PC/PS giant unilamellar vesicles even at temperatures below the liquid/gel phase transition (29). In contrast, annexin A5 bound to the surface of PC/PS-supported lipid bilayers was found to be totally immobile below the liquid/gel transition, suggesting the nonslip diffusion mode (64). Of importance, the majority of proteins with polybasic domains are also lipidated, which should effectively prevent their membrane skating. This conjecture is supported by the fact that these proteins diffuse more slowly than the surrounding free lipids, according to several measurements of their mobility in vivo. In our model, we therefore explored the nonslip mode of protein dynamics. In the Monte-Carlo simulations, this choice allowed us to avoid kinetic trapping of the peptide, which otherwise would result in a lateral dynamics stalemate as observed by us and others (54).

In agreement with previously published results (29), we find in our model that the peptide representing a polybasic domain interacts very differently with monovalent lipids (PS) and PIP₂. The duration of its association with PIP₂ indicates that they diffuse as a complex. In contrast, interaction with individual PS lipids is predicted to be fleeting (∼${10}^{-6}\sec$) and likely undetectable in experiment. This result, however, is not in contradiction to the existence of a dynamic shell of monovalent lipids (see Fig. 3) that continuously forms and disassembles around the diffusing peptide due to the recruitment and release of lipids.

Consistent with previous experimental results, our model suggests that homogeneously distributed anionic lipids, when present at physiological concentrations, only slightly reduce the diffusion coefficients of proteins with polybasic domains and do not qualitatively change their lateral dynamics. However, we predict that spatially heterogeneous distributions of monovalent lipids can cause systematic drift of such proteins along or against the lipid density gradient depending on the sign of the total charge. The rapid conversion of abundant neutral lipid PC by phospholipase D into monovalent phosphatidic acid (PA) followed by its rapid dephosphorylation into electroneutral DAG (65) is one example of a biologically relevant process that results in such a heterogeneous lipid distribution. To affect the spatial distribution of proteins with polybasic domains, such gradients need not be long-lived. Indeed, in the above example with the 0.3%/nm gradient, a protein could traverse 100 nm within only 0.03 s. We therefore speculate that heterogeneous distributions of charged lipids that are routinely generated by signaling events throughout normal cellular activity could be sufficient to perturb the spatially homogeneous distribution of important signaling proteins, with potentially significant physiological consequences. Further experimental and theoretical work is required to validate and extend this hypothesis.