Figure 4.

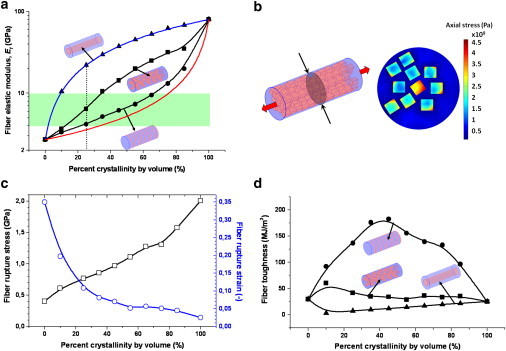
Variation of the mechanical properties with respect to the silk fiber crystallinity. (a) The effects on the fiber elastic modulus, E_f, are shown. Results for three different crystalline subunit distributions are shown as indicated by the schematics. The parallel (triangles) and serial (circles) distributions obey simple two-phase isotropic models, namely, the Voigt composite model (blue line) for the parallel distribution: E_f = E_cu_c + E_au_a and the Reuss composite model (red line) for the serial distribution: 1/E_f = u_c/E_c + u_a/E_a, where E_c, u_c, and E_a, u_a are the elastic moduli and volume percentage of the crystalline and amorphous subunits, respectively. The small discrepancy with the Reuss model is due to the geometric effects arising from nonzero Poisson's ratios used in three-dimensional FE simulations. The random distribution (squares) yields intermediate values for E_f. (Dashed line) Percent crystallinity of dry spider silk in nature. Green band spans the interval of experimental values from literature (1,31–33). (b) Schematic of the comprehensive fiber model with random distribution of crystals (left) and the stress distribution at an arbitrary cross section of a 25% crystalline fiber with an external stress of 0.8 GPa (right). (c) Variation of the rupture stress (squares) and rupture strain (circles) with respect to the fiber crystallinity, again for a fiber with random distribution of crystals. Values for 0% crystallinity were calculated with the all-atom model. (d) Variation of the toughness with respect to the silk fiber crystallinity. Results for the parallel (triangles), serial (circles), and random (squares) distribution states of the crystalline subunits are shown as indicated by the schematics. Smooth lines in panels a, c, and d are spline fits for the data points.