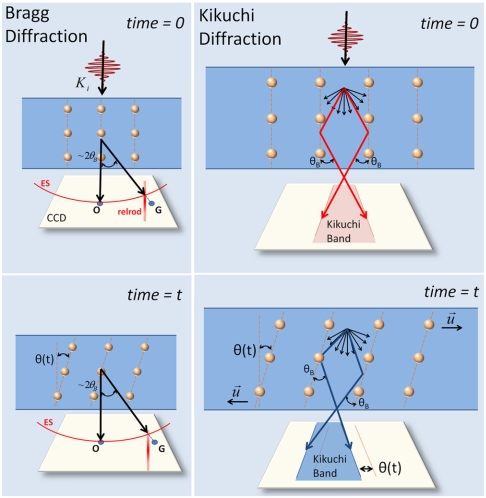
Fig. 2.
Kikuchi and Bragg diffraction dynamics. Specifically shown is the effect of transverse elastic waves on Bragg (Left) and Kikuchi (Right) diffractions. The Bragg spot G in the zero-order-Laue-zone, corresponding to the planes parallel to the incident electron beam, is defined by intersection of the Ewald sphere (ES) and the relrod in the reciprocal space. The tilt θ(t) of atomic planes at a time t causes this intersection point to move along the relrod, resulting in an intensity change but with no change in position on the CCD.* On the other hand, Kikuchi diffraction (Right) is a result of diffusely scattered electrons (black arrows) undergoing a second scattering from the atomic planes with a Bragg angle θB. Because the span of angles after the diffuse scattering is large, there are always electrons that will exactly satisfy the Bragg condition (shown with red and dark-blue arrows at time = 0 and time = t, respectively). Hence, Kikuchi lines will shift on the CCD by an amount proportional to atomic plane tilts θ(t), which enables us to directly measure the polarization amplitude and direction of the shear deformations. This schematic depiction is simplified in several ways: (i) The result of the diffuse scattering is actually a cone in three dimensions and the Bragg condition is satisfied along lines (or parabolas) that appear as Kikuchi lines on the CCD, in contrast to the left-panel case where the Bragg condition is satisfied along one direction only (and hence only one spot on the CCD). (ii) The space between the Kikuchi lines is filled and they appear as bands for thick enough samples. (iii) The objective lens that actually forms the diffraction pattern on the CCD is omitted for simplicity.