Abstract
According to contextual-variability theory, experiences encoded at different times tend to be associated with different contextual states. The gradual evolution of context implies that spaced items will be associated with more distinct contextual states, and thus have more unique retrieval cues, than items presented in proximity. Ross and Landauer (1978) tested this theory by examining whether the probability of recalling at least one of two studied items should increase as a function of the items’ spacing. Their failure to observe this result was taken as strong evidence against contextual variability theory. We replicated their analysis on six recall datasets. For all of these datasets we found the pattern of results predicted by contextual-variability theory. These findings provide critical support for contextual-variability theories of episodic memory.
Introduction
One of the major puzzles in human learning and memory concerns the way people distinguish two nominally identical events that have occurred at different times. To explain this puzzle, memory theorists have often invoked the concept of contextual variability. Contextual variability theories propose that each experience is recorded in relation to a context representation that evolves slowly over time, as a consequence of both external stimulating conditions and changes in an internal mental context representation. One of the earliest formalizations of this idea can be found in Estes’ stimulus sampling theory, which has been used to explain a number of diverse phenomena in both human and animal learning, including the phenomena of spontaneous recovery of previously learned associations (Estes, 1955b,a). Contextual variability theories were subsequently proposed to account for data on recognition memory, frequency, and recency judgments (e.g., Bower, 1972), interference effects in paired associate learning (Mensink and Raaijmakers, 1988), recency effects in immediate, delayed, and continual distractor free recall (Glenberg and Swanson, 1986; Sederberg et al., 2008), and the contiguity effect in free recall (Howard and Kahana, 1999, 2002).
Contextual variability theory has also been proposed to explain the beneficial effects of spaced practice (e.g. Melton, 1970; Madigan, 1969). The greater the spacing between two items, the more contextual drift will have taken place between their presentations. When repeated presentations of an item are massed, the item’s associated contexts are highly similar, and as such, the set of effective cues for either of the items’ presentations will be small. When the presentations of a repeated item are spaced, there is a diversification advantage: a larger set of contextual cues will be effective in allowing participants to target either one or the other of the presentations.
Despite the theoretical successes of contextual variability, as well as its psychological appeal, efforts to provide direct empirical support for this idea have largely failed. Arguably the most striking failure of contextual variability can be found in a study by Ross and Landauer (1978). The authors note that contextual-variability theories apply to both repeated and nonrepeated items. Given that the probability of recalling an item repeated in positions i and j is equivalent to the probability of recalling either the occurrence of the item in position i or the occurrence of the item in position j, Ross and Landauer (1978) investigated how the probability of recalling either of two once-presented items in positions i and j changes with their spacing. They introduced the OR score, the probability of recalling one item or the other, inclusively. Contextual-variability theory predicts that the OR score should increase as a function of the items’ spacing. However, Ross and Landauer (1978) found that OR scores do not increase as a function of the spacing, or lag, between items.
In the present paper we attempt to replicate the null result reported by Ross and Landauer (1978) through a reanalysis of six large free recall studies reported by Murdock (1962); Kahana and Howard (2005); Bridge (2006), and Polyn et al. (2009). Contrary to Ross and Landauer (1978), we find a significant increase in OR scores for all studies. These findings vindicate the contextual variability account that was sharply challenged by Ross and Landauer’s null result.
Methods
We analyzed data from six free recall studies involving lists of at least 24 items, and for which we could obtain data on the sequence of responses that participants made on each trial. We limited our analyses to studies using longer lists so that we could examine the OR score effect across a range of lags after excluding items from the primacy and recency portions of the serial position curve. After describing the experimental methods used in each of these studies we present our methodology for calculating OR scores and correcting for the effects of serial position.
Murdock (1962)
Each participant performed immediate free recall on 80 lists of words. Each list comprised words chosen randomly and without replacement from the Thorndike and Lorge (1944) word pool with G count > 20. Participants were given 90 s to for written recall of as many items as they could remember. Among the six list-length and presentation-rate conditions we restricted our analyses to lists of 30 or 40 items presented at a 1 second rate. 15 participants contributed to each condition.
Kahana and Howard (2005)
65 participants performed delayed free recall of lists with either massed or spaced repetitions of 30 nouns drawn from the Toronto word pool (Friendly et al., 1982). Words were presented auditorally at a rate of one per 1500 ms. We restricted our analyses to the massed condition, in which each word was presented three times in succession for a total presentation duration of 4500 ms. For the purposes of the present study, we defined the serial position of each item as its position in the thirty-item list of unique words presented. Thus, although the words are nominally repeated, each unique word had an unambiguous serial position. After the presentation of the last item, participants performed arithmetic problems of the form A + B + C =?, where A, B, and C were positive, single-digit integers, until they answered 15 problems correctly in a row. After completing the self-paced distractor task, which took on average 45 s, participants were given 90 s to vocally recall the list.
Bridge (2006)
119 participants performed free recall of 18 lists. Each list comprised 25 nouns drawn from the Toronto Word Pool. During each word presentation, participants were given 1,100 ms to judge whether the word was “concrete” or “abstract”. Once they made their response, a 200 ms ISI period was initiated. After the presentation of the last item, participants performed arithmetic problems of the form A + B + C =?, where A, B, and C are positive, single-digit integers, for 30 s. After this distractor task, participants were given 60 s to vocally recall the list.
Polyn et al. (2009)
45 participants performed immediate free recall of 34 total lists. Each list comprised 24 items selected from the word association spaces norms (WAS; Steyvers et al., 2004). For each item, participants made either a size or animacy judgment. Items were presented visually for 3000 ms, with an 800 ms ISI, and participants indicated their response during this time via a keypress. After the final item, participants were given 90 s to vocally recall the list. On single-task lists, every word was judged with the same task. On task-shift lists, participants shifted back and forth between the two judgment tasks. We restricted our analyses to the single-task lists.
Polyn et al. (2009) replication
60 participants performed immediate free recall of 48 total lists. The screen was blank for a 1000 ± 200ms ISI between each word. All other procedures were identical to Polyn et al. (2009).
OR Score Analysis
Following Ross and Landauer (1978), an OR score is defined as the probability of recalling either of two once-presented items. Defining the lag of any pair of list items as the difference in their serial positions, we calculated for each participant in each study, the mean OR score across all serial position pairs with a given lag (items in serial positions 4 and 3 would have a lag of 1). We considered lags in the range of 1–6 as pairs with large lags have far less data than pairs with small lags.
In using OR scores to evaluate contextual variability theory, it is important to control for serial position effects. This is because more widely separated word pairs will be more likely to occupy primacy and/or recency positions where recall is elevated. As such, pairs of words with increasing lag will tend to have higher OR scores simply due to serial position effects. In evaluating the effect of lag on OR scores, we therefore excluded the primacy and recency portions of the serial position curve. To determine the extent of the primacy effect in each data set, we scanned the list starting from serial position 1 to find the first pair of two successive serial positions for which the mean recall probability did not differ significantly from the preceding pair. For example, we used a paired-sample t-test to compare the mean probability of recall at serial positions 1 and 2 with the mean probability of recall at serial positions 3 and 4. If these two distributions were reliably different (p < 0.05), then we continued to scan the list by comparing . Once we reached a serial position n such that was not reliably different from , we assumed that we were in the flat mid-list portion of the serial position curve (Murdock, 1962). We determined the recency portion of the serial position curve in a similar way. We compared recall probability for neighboring pairs of serial positions, starting at the end of the list, until we reached some serial position m > n such that was reliably different from was not reliably different from . We would thus include serial positions n to m in our analysis. On average, this led to the removal of 2.3 ± 0.5 primacy serial positions and 5.0 ± 1.1 recency serial positions.
Although the preceding analysis allows us to remove aggregate-level serial position effects, we sought to further control for serial position effects at the level of individual participants. This is important because some participants exhibit stronger primacy or stronger recency than is evident in the average data. We determined the OR scores expected if recall at each serial position is independent of recall at all other serial positions (marginal OR scores). If a participant’s probability of recall at serial position i is P(i), then the marginal OR score at lag l is: OR(l) = < P(i) + P(i + l) − P(i)P(i + l) >i. This follows from the definition of independence in probability theory. We define a participant’s adjusted OR score as the difference between the observed and marginal OR scores. All statistical analyses were performed on these adjusted OR scores. In the Figures shown below, each participant’s expected marginal OR score, < 2P(i) − P(i)2 >i was added to the adjusted OR scores at every lag.
Temporal clustering analysis
To quantify the contiguity effect we computed a percentile-based measure of each participant’s tendency to cluster responses according to the temporal structure of the list (Polyn et al., 2009, henceforth, the temporal clustering score;). For each output position, we determine the absolute value of the lags between the serial positions of the just-recalled word and the set of not-yet-recalled words. The clustering score at this output position is defined as the proportion of the possible lags greater than the observed lag. Participants who exhibit a strong degree of temporal organization produce high clustering scores, as temporal clustering will cause observed lags to be smaller than average. A participant with a maximum clustering value of 1 always transitions to the available item with the smallest absolute lag relative to the just-recalled item. A clustering score of 0.5 would indicate that transitions were just as likely to be to an neighboring item as to a remote item.
Results
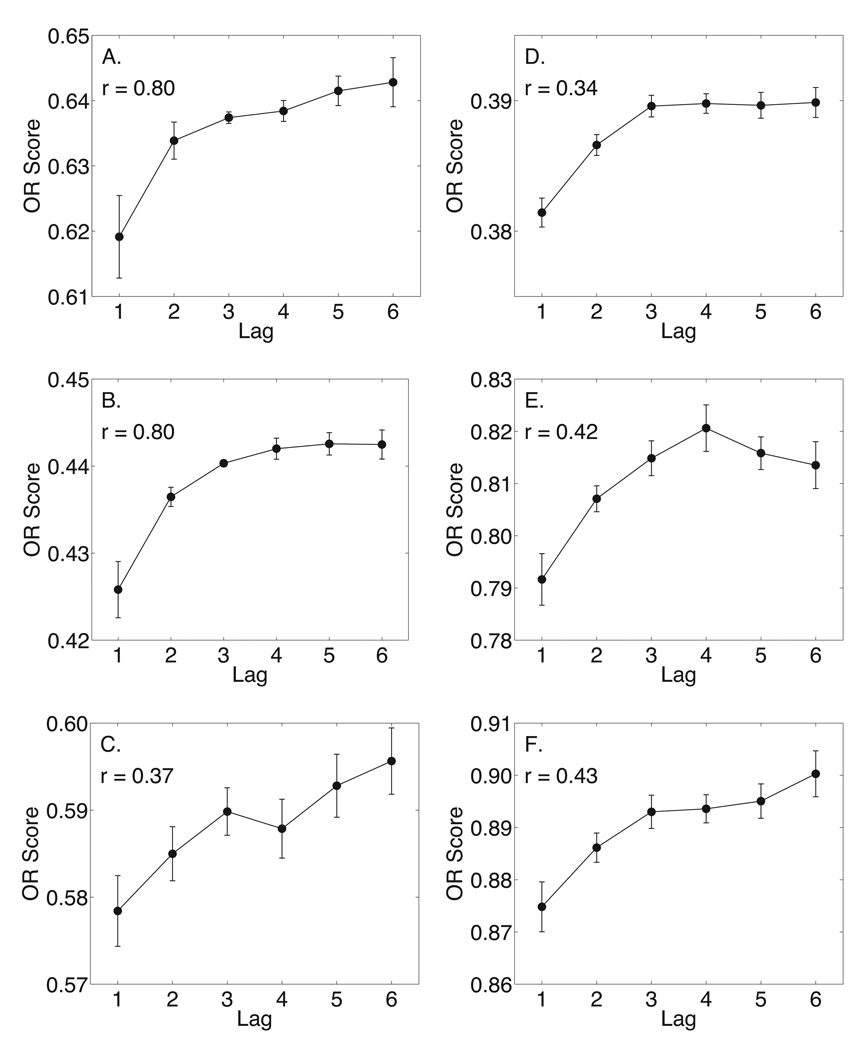
To test the contextual variability hypothesis, we performed the OR score analysis of Ross and Landauer (1978) on six free recall data sets (see Methods). In each of these datasets, we found OR scores to increase reliably with lag (see Figure 1). These results indicate that as the lag between a pair of items increases, the probability of recalling at least one item from that pair also increases, as predicted by contextual-variability theory.
Figure 1. The OR score effect.
For each of the six studies OR scores increased reliably with the lag between the studied items. The mean lag-OR score correlation across participants is reported in each panel. The distribution of correlation coefficients is significantly positive for each study (p < 0.005). Error bars represent Loftus and Masson (1994) 95% confidence intervals. A. Murdock (1962), list-length = 30. B. Murdock (1962), list-length = 40. C. Kahana and Howard (2005). D. Bridge (2006). E. Polyn et al. (2009). F. Polyn et al. (2009) replication.
We refer to the positive correlation between OR scores and lag as the OR score effect. Each of the six studies analyzed here exhibits a significant OR score effect, indicating that this effect is robust across experimental conditions. Computing the correlation between OR score and lag separately for each participant, we found nearly 10 times as many participants with correlations above +0.30 than with correlations below −0.30 (66% and 7%, respecitvely).
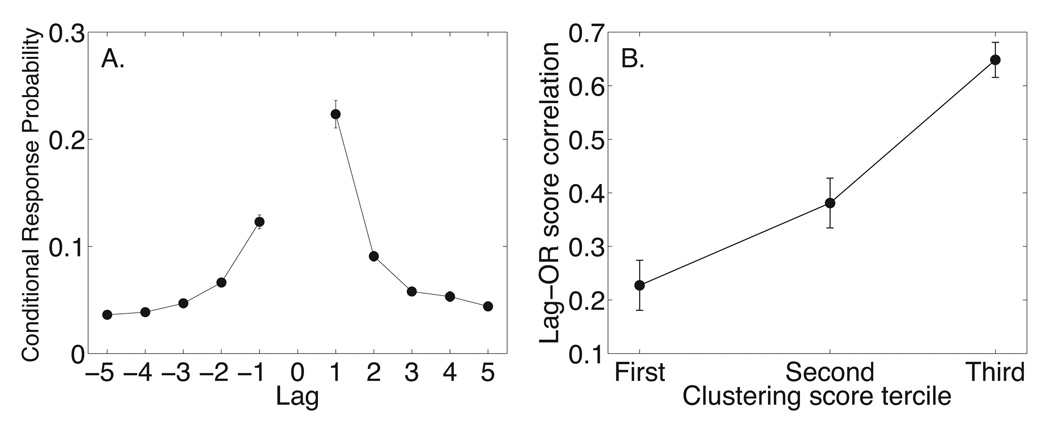
A significant OR score effect suggests that recall of items depends on the contexts associated with those items. The order in which items are recalled depends on their associated contexts as well. In free recall, therefore, recalls may be organized according to the order in which items were presented (their temporal organization). To examine the effects of the temporal organization of the list on free recall transitions, Kahana (1996) measured the conditional response probability as a function of lag (the lag-CRP). Given that a participant has just recalled an item from serial position i, the lag-CRP indicates the probability that the next item recalled comes from serial position i + lag. Lag-CRP analyses have revealed a striking contiguity effect in free recall—neighboring items in the study list tend to be recalled successively with a strong forward bias (see Kahana et al., 2008, for a review). This can be seen in Figure 2A, which shows the lag-CRP across the six studies included in our analyses. The contiguity effect seen in the data implies that recall of neighboring items are not independent. The appendix presents a simple proof to demonstrate that such non-independence implies the existence of an OR score effect in the data.
Figure 2. The relation between contiguity and OR score effects.
A. The conditional-response probability as a function of lag (or lag-CRP) shows the probability of recalling an item from serial position i + lag immediately following an item from serial position i. This curve depicts data averaged across the studies included in our meta-analysis: Murdock (1962), Kahana and Howard (2005), Bridge (2006), Polyn et al. (2009), and Polyn et al. (2009) replication. Error bars represent Loftus and Masson (1994) 95% confidence intervals. B. Using a percentile-based measure of the contiguity effect (Polyn et al.’s temporal clustering score) we examined whether participants who exhibited strong contiguity effects also exhibited a strong OR score effect (quantified as the lag–OR score correlation). We divided participants into terciles according to their clustering score. Error bars represent 95% confidence intervals.
Contextual-variability theory asserts that items presented further apart have less correlated contextual representations. To the extent that temporal clustering, as seen in the contiguity effect, is driven by the overlap in the contextual representations of neighboring items, the theory predicts that participants who exhibit a stronger contiguity effect would also exhibit a larger OR score effect. To test this prediction, we quantified the OR score effect for each participant as the lag–OR score correlation and we quantified the contiguity effect using the temporal clustering score of Polyn et al. (2009) (see Methods). We found a strong positive correlation between the contiguity effect and of the OR score effect (r = 0.42, p < 0.0001). Figure 2B shows this positive relation by grouping participants into terciles based on their clustering scores.
Discussion
According to contextual-variability theory, context evolves as each list item is presented. As the lag between items i and j increases, their associated contexts become less similar. Items associated with more varied contexts should be more easily recalled than items associated with the same context because each distinct context provides an additional retrieval path to the items. Contextual-variability theory thus predicts that the probability of recalling either i or j increases with lag between the two items. Consistent with this prediction, we found a significant positive correlation between lag and OR score. We also found a significant positive correlation between participants’ OR score effect and their temporal clustering scores. Participants who organized their recalls more strongly according to temporal context exhibited stronger OR score effects.
Our finding of significant OR score effects in six free recall experiments that varied in presentation modality, presentation rate, encoding task, and list-length raises an obvious question. Why did Ross and Landauer (1978) fail to observe this effect? Ross and Landauer’s methodology possessed a number of idiosyncratic features. Rather than studying items presented one at a time, as is standard in free recall experiments, they presented pairs of items on study cards. They also used a very long single list and a delayed free recall test. Participants were given a recognition test following free recall, but it was not clear whether they were instructed to study the pairs expecting a recognition test, a recall test, or both. Although it is tempting to speculate on whether these procedural differences, or differences in statistical power, may have limited their ability to detect the OR score effect we are reluctant to do so. Given that our results appear consistently across the six experiments analyzed, we suspect that they are a general feature of free recall, at least for lists of individually presented items.
Although Ross and Landauer failed to observe evidence for fluctuations in context at the level of individual list items, Glenberg and Lehmann (1980) did report a significant OR score effect for items from different lists studied on different days. Their result would imply that context varies across experiences that are widely separated in time, and presumably distinguished by the events surrounding each experimental session. Our finding of an OR score effect at the level of individual items within a list supports a much stronger prediction of contextual variability theory—namely, that fluctuations in context occur at the level of item presentations with a single list presumably studied within a single situational context.
Ross and Landauer (1978) introduced the OR score analysis to test contextual variability theories of the spacing effect. The spacing effect is a very robust phenomenon in free recall: people recall a greater proportion of spaced items than massed items, and the recall advantage for spaced items increases with the lag between the repetitions (Madigan, 1969; Melton, 1970). Although we did not analyze the OR score effect in lists with spaced repetitions, contextual variability has played a prominent role in theories of the spacing effect, and Ross and Landauer’s failure to observe an OR score effect is often used to refute these theories. As such, we briefly consider how our finding of significant OR score effects in six free recall studies bears on theories of the spacing effect.
The probability of recalling an item repeated in positions i and j is equivalent to the probability of recalling either the occurrence of the item in position i or the occurrence of the item in position j. The OR score is the parallel calculation for non-repeated items: the probability of recalling either of two once-presented items in positions i and j. Whereas the finding of a significant OR score effect supports the notion of contextual variability, the size of the effect is substantially smaller than the advantage of spaced repeated items in free recall (e.g.,Madigan, 1969; Melton, 1970). The great difference in magnitudes, coupled with the intricate pattern of results in the spacing literature, suggests that contextual variability alone cannot fully explain the spacing phenomena.
Study-phase retrieval is one of several alternative mechanisms that have been proposed to explain spacing effects, especially in free recall tasks (Greene, 1989). Study-phase retrieval assumes when an item is repeated, it is not simply associated with a context state. Rather, the state of context is updated by retrieving the contexts associated with that item from when it was presented previously, and adding those to the current state of context (Howard and Kahana, 2002; Sederberg et al., 2008). Thus, the context at the time of the second presentation includes the context associated with the earlier presentation of the item. This means, effectively, that the context representation after the second presentation of a repeated item is more similar to the context of the first presentation than in the case of unrelated words. Under the assumptions of study-phase contextual retrieval, the time-of-test context will be more similar to contexts of a repeated item than would be the case for a list with non-repeated items. For an item presented in serial positions i and j, study-phase retrieval strengthens the association between the item’s contexts at presentations i and j. Since the presentation at j is closer to the time-of-test context than i, retrieving context i at presentation j also strengthens the association between context i and the time-of-test context. This additional advantage does not apply to once-presented items. The interaction between contextual retrieval and study-phase retrieval both tightens the episodic associations among the repeated items in the list, and moves their representations closer to that of the time-of-test context cue. Thus, study-phase retrieval could greatly magnify the effect of contextual variability. In support of this logic, Raaijmakers (2003) successfully fit a wide range of spacing phenomena in recall tasks by incorporating study-phase retrieval into a contextual-variability model of episodic recall. Without this assumption, it is unlikely that Raaijmaker’s model would have been nearly as successful.
In studies of the spacing effect, one cannot observe the effect of contextual variability in isolation. Although the principles of contextual variability apply to both repeated and non-repeated items, study-phase retrieval applies only to repeated items. Thus, analyses of OR scores performed on non-repeated items reflect the role of contextual variability only; analyses on recall of repeated items reflect the interaction between contextual variability, study-phase retrieval, and other mechanisms related to repetition of items (e.g., deficient processing of massed repetitions).
In conclusion, the probability of recalling at least one item from a pair increases as the contexts between those items become less correlated. This result implicates a stronger role for contextual variability in free recall than previous studies have suggested.
Acknowledgements
This research was funded by National Institutes of Health grant MH55687 and by a grant from the Dana Foundation.
Appendix: The OR score effect and dependency between recalls
Let P(io) denote the probability of recalling at output position o the item presented at serial position i. Suppose j and k are two serial positions such that |j − i| < |k − i|. The contiguity effect implies that:
P(jo|io−1) > P(ko|io−1).
by conditional probability definitions.
P(jo, io−1) > P(ko, io−1) from multiplying by P(io−1).
Generalizing the idea of the contiguity effect across output positions yields:
| (A.1) |
We use Inequality A.1 to formally state the dependency between recalls at serial positions.
Theorem. Suppose Inequality A.1 holds. If we consider probabilities only in the flat portion of the serial position curve (i.e. excluding primacy and recency portions), then P(i OR j) < P(i OR k).
Proof. Multiplying Inequality A.1 by −1, and then adding P(i) + P(j) + P(k) to both sides:
We can rearrange terms so that on each side of the inequality sign, the first three terms represent the probability of recalling at least one of two items:
Under the assumption that we are at the flat portion of the serial position curve, we can define a small ε such that
By transitivity,
In the limit as ε → 0,
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bower GH. Stimulus-sampling theory of encoding variability chapter 5. In: Melton AW, Martin E, editors. Coding Processes in Human Memory. New York: John Wiley and Sons; 1972. pp. 85–121. [Google Scholar]
- Bridge D. Unpublished Honor’s thesis. Syracuse University; 2006. Memory and cognition: What difference does gender make? [Google Scholar]
- Estes WK. Statistical theory of distributional phenomena in learning. Psychological Review. 1955a;62:369–377. doi: 10.1037/h0046888. [DOI] [PubMed] [Google Scholar]
- Estes WK. Statistical theory of spontaneous recovery and regression. Psychological Review. 1955b;62:145–154. doi: 10.1037/h0048509. [DOI] [PubMed] [Google Scholar]
- Friendly M, Franklin PE, Hoffman D, Rubin DC. The Toronto Word Pool: Norms for imagery, concreteness, orthographic variables, and grammatical usage for 1,080 words. Behavior Research Methods and Instrumentation. 1982;14:375–399. [Google Scholar]
- Glenberg AM, Lehmann TS. Spacing repetitions over 1 week. Memory & Cognition. 1980;8:528–538. doi: 10.3758/bf03213772. [DOI] [PubMed] [Google Scholar]
- Glenberg AM, Swanson NG. A temporal distinctiveness theory of recency and modality effects. Journal of Experimental Psychology: Learning, Memory & Cognition. 1986;12:3–15. doi: 10.1037//0278-7393.12.1.3. [DOI] [PubMed] [Google Scholar]
- Greene RL. Spacing effects in memory: Evidence for a two-process account. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1989;15:371–377. [Google Scholar]
- Howard MW, Kahana MJ. Contextual variability and serial position effects in free recall. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:923–941. doi: 10.1037//0278-7393.25.4.923. [DOI] [PubMed] [Google Scholar]
- Howard MW, Kahana MJ. A distributed representation of temporal context. Journal of Mathematical Psychology. 2002;46:269–299. [Google Scholar]
- Kahana MJ. Associative retrieval processes in free recall. Memory & Cognition. 1996;24:103–109. doi: 10.3758/bf03197276. [DOI] [PubMed] [Google Scholar]
- Kahana MJ, Howard MW. Spacing and lag effects in free recall of pure lists. Psychonomic Bulletin & Review. 2005;12:159–164. doi: 10.3758/bf03196362. [DOI] [PubMed] [Google Scholar]
- Kahana MJ, Howard MW, Polyn SM. Associative retrieval processes in episodic memory. In: Roediger HL III, editor. Cognitive psychology of memory. Vol. 2 of Learning and memory: A comprehensive reference, 4 vols. (J. Byrne, Editor) Oxford: Elsevier; 2008. [Google Scholar]
- Loftus GR, Masson MEJ. Using confidence intervals in within-subject designs. Psychonomic Bulletin & Review. 1994;1:476–490. doi: 10.3758/BF03210951. [DOI] [PubMed] [Google Scholar]
- Madigan SA. Intraserial repetition and coding processes in free recall. Journal of Verbal Learning and Verbal Behavior. 1969;8:828–835. [Google Scholar]
- Melton AW. The situation with respect to the spacing of repetitions and memory. Journal of Verbal Learning and Memory. 1970;9:596–606. [Google Scholar]
- Mensink GJM, Raaijmakers JGW. A model for interference and forgetting. Psychological Review. 1988;95:434–455. [Google Scholar]
- Murdock BB. The serial position effect of free recall. Journal of Experimental Psychology. 1962;64:482–488. [Google Scholar]
- Polyn SM, Norman KA, Kahana MJ. A context maintenance and retrieval model of organizational processes in free recall. Psychological Review. 2009;116:129–156. doi: 10.1037/a0014420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raaijmakers JGW. Spacing and repetition effects in human memory: application of the sam model. Cognitive Science. 2003;27:431–452. [Google Scholar]
- Ross B, Landauer T. Memory for at least one of two items: Test and failure of several theories of spacing effects. Journal of Verbal Learning and Verbal Behavior. 1978;17:669–680. [Google Scholar]
- Sederberg PB, Howard MW, Kahana MJ. A context-based theory of recency and contiguity in free recall. Psychological Review. 2008;115:893–912. doi: 10.1037/a0013396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steyvers M, Shiffrin RM, Nelson DL. Word association spaces for predicting semantic similarity effects in episodic memory. In: Healy AF, editor. Cognitive Psychology and its Applications: Festschrift in Honor of Lyle Bourne, Walter Kintsch, and Thomas Landauer. Washington, DC: American Psychological Association; 2004. [Google Scholar]
- Thorndike EL, Lorge I. The teacher’s word book of 30,000 words. NY: Bureau of Publications, Teachers College xii; 1944. [Google Scholar]