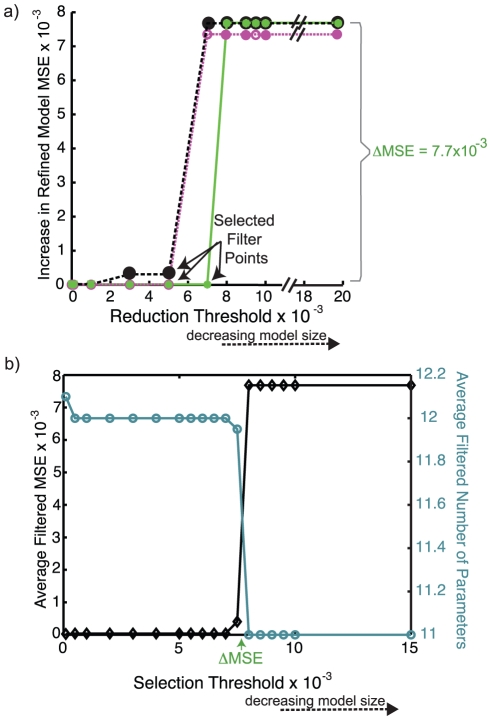
Figure 3. Reduction of trained cFL models.

The unprocessed models resulting from twenty independent runs of the discrete genetic algorithm to train the expanded network to an in silico dataset were reduced using several reductions thresholds and subsequently refined. The behavior of three representative models is shown (a). To develop a criterion for our model selection, we note that each individual model exhibits a drastic increase in refined MSE when reduced at some reduction threshold. For our toy model, the MSEs of some reduced-refined models increase significantly (ΔMSE of 7.7x10⁻³) at a reduction threshold of greater than 5×10⁻³ (a., magenta line), whereas the MSEs of others only increase at a reduction threshold greater than 7×10⁻³ (a., green line). This increase in MSE of 7.7×10⁻³ is deemed significant because it corresponds to the models no longer fitting the in silico data of Akt and JNK under TGFα stimulation (the remaining data are still well fit). For each unprocessed model, we refer to the reduction threshold above which a significant increase in MSE is observed as the ‘filter point’ of the model. Each individual model has a filter point that is determined based on the amount that the reduced-refined model's MSE is allowed to increase. We term this allowable increase in MSE the ‘selection threshold’. For example, one model of our toy example (black line) could be described as having a filter point of 1×10⁻³ or 5×10⁻³, depending on the amount of increase in MSE allowed by the selection threshold. To choose a selection threshold, we compare the average increase in final MSE to the average decrease in the number of parameters in the resultant filtered family of models (b) and note that, at a selection threshold of 7.7×10⁻³, the average MSE increases while at a selection threshold of 5×10⁻⁴, average number of parameters decreases. Thus, a selection threshold of 5×10⁻⁴ to 7.6×10⁻³ results in the models at the “filter points” noted in (a).