Quantum mechanics/molecular mechanics investigation of the mechanism of phosphate transfer in human uridine-cytidine kinase 2

Abstract

The mechanisms of enzyme-catalyzed phosphate transfer and hydrolysis reactions are of great interest due to their importance and abundance in biochemistry. The reaction may proceed in a stepwise fashion, with either a pentavalent phosphorane or a metaphosphate anion intermediate, or by a concerted S_N2 mechanism. Despite much theoretical work focused on a few key enzymes, a consensus for the mechanism has not been reached, and examples of all three possibilities have been demonstrated. We have investigated the mechanism of human uridine-cytidine kinase 2 (UCK2, EC 2.7.1.48), which catalyzes the transfer of a phosphate group from ATP to the ribose 5′-hydroxyl of cytidine and uridine. UCK2 is normally expressed in human placenta, but is overexpressed in certain cancer cells, where it is responsible for activating a class of antitumor prodrugs. The UCK2 mechanism was investigated by generating a 2D potential energy surface as a function of the P–O bonds forming and breaking, with energies calculated using a quantum mechanics/molecular mechanics potential (B3LYP/6–31G(d):AMBER). The mechanism of phosphate transfer is shown to be concerted, and is accompanied by concerted proton transfer from the 5′-hydroxyl to a conserved active site aspartic acid that serves as a catalytic base. The calculated barrier for this reaction is 15.1 kcal/mol, in relatively good agreement with the experimental barrier of 17.5 kcal/mol. The interactions of the enzyme active site with the reactant, transition state, and product are examined for their implications on the design of anticancer prodrugs or positron emission tomography (PET) reporter probes for this enzyme.

Introduction

Phosphate transfer and hydrolysis reactions are the basis of kinase and phosphatase signaling pathways, which are vital for cellular function and growth regulation.^1,2 The transfer of phosphate groups is also the reaction catalyzed by the nucleic acid polymerases, which synthesize DNA and RNA.^3,4 Hydrolysis of adenine triphosphate (ATP) is believed to provide the energy for the power stroke of cellular motors such as myosin⁵ and the mitochondrial protein import complex,⁶ while enzyme-catalyzed phosphorylation converts certain anticancer prodrugs to their active forms in tumor cells⁷ and also creates an electrostatic barrier to the extracellular diffusion of positron emission tomography (PET) probes such as ¹⁸F-2-fluoro-2-deoxyglucose (¹⁸F-FDG).^8,9 Due to their importance in both natural biochemistry and therapeutic pharmacology the mechanisms of phosphate transfer and hydrolysis reactions are of great interest.

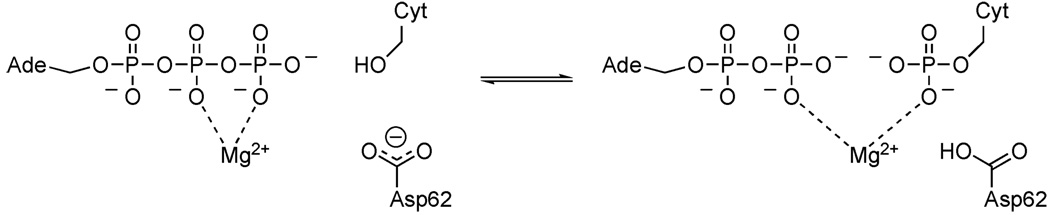
Here we have initiated a study investigating the mechanism of the human uridine-cytidine kinase 2 (UCK2, EC 2.7.1.48) enzyme. UCK2 catalyzes the phosphorylation of uridine and cytidine nucleosides to their monophosphate forms, with ATP as the phosphate group donor. The reaction is assisted by a magnesium ion, and the active site includes a conserved aspartate, Asp62, which has been hypothesized to function as a general base (Fig. 1).¹⁰ In contrast to the ubiquitous expression of UCK1, UCK2 is normally expressed only in the placenta.¹¹ UCK2 is overexpressed in certain cancer cells including particular genotypes of Burkitt lymphomas and acute lymphoblastic leukemias.¹² It is responsible for phosphorylating the antitumor prodrugs 3′-C-ethynylcytidine and 3′-C-ethynyluridine to produce their active forms.⁷

Fig. 1.

Phosphate transfer reaction catalyzed by UCK2. ATP is the phosphate group donor. The phosphate acceptor shown is cytidine, although other pyrimidines such as uridine are also phosphorylated.

In addition, UCK2 is a member of the same protein fold family as the prominent PET reporter protein, herpes simplex virus 1 thymidine kinase (HSV1-TK).¹⁰ HSV1-TK phosphorylates substrates that contain a positron-emitting isotope and thereby traps the phosphorylated form inside the cells that have been engineered to express HSV1-TK. The positrons emitted by the phosphorylated reporter substrate are then detected to image the location of HSV1-TK in living subjects.^13–16 This reporter/probe system holds promise for future therapeutic use in humans;^17–19 however, there is the potential for the development of an immune response against the exogenous enzyme, which may limit its use in some patients.^20,21 This has led to parallel investigations into human PET reporter genes such as the human mitochondrial thymidine kinase type 2.²² Human UCK2, by virtue of its selective expression and non-immunogenicity, may represent a potential PET reporter enzyme for which substrates could be designed. Any PET probes developed for wild-type UCK2 might also be useful for the specific imaging of cancer cells that overexpress UCK2.^23–25

The possible mechanisms for phosphate transfer reactions may be placed on a continuum between completely associative, in which there is a stable pentavalent phosphorane intermediate, and completely dissociative, in which there is a stable metaphosphate anion formed before the transfer is completed by bond-formation to give the product state. In between these extremes is a concerted S_N2 mechanism that is characterized by a single TS in the absence of an intermediate. The TS for this mechanism can be further differentiated by the degree of bond formation and bond cleavage at the transition state, with relatively associative or relatively dissociative S_N2 mechanisms possible.²⁶ These reaction paths are shown schematically in Fig. 2. Fig. 2 is a variant of the More O’Ferrall–Jencks diagrams that have been used to describe nucleophilic substitution reactions.^27–29 The form of the More O’Ferrall–Jencks diagram lends these reactions to computational investigation by its reference to the potential energy surface (PES). The PES will show the most favored, lowest energy path between the reactants and products, as well as if multiple mechanisms are possible. The PES has been used extensively by Warshel and co-workers to investigate similar reactions.^26,30,31

Fig. 2.

Mechanisms for general base-catalyzed phosphate transfer. The red path is associative, with a stable phosphorane intermediate, while the blue path is dissociative, with a stable metaphosphate intermediate. Figure adapted from ref. 41.

The method of choice for computing reaction mechanisms of enzymes is a hybrid of quantum mechanics and molecular mechanics (QM/MM), in which the reacting part of the system is treated quantum mechanically and the rest of the system is represented with molecular mechanics calculations.^32–35 QM/MM methods have been applied extensively to enzyme-catalyzed reactions, including many phosphate transfer and hydrolysis reactions.^31,36–47 Although the most common conclusion has been to favor the concerted S_N2 mechanism,^31,42–47 a general consensus has not been reached. Previous work has also found examples of completely associative^36–39 and completely dissociative mechanisms.^40,41 These findings suggest that the mechanism of each individual reaction may be dependent on the specific reactants as well as the surrounding environment.

QM/MM methods have been used here to calculate a 2-dimensional potential energy surface in the dimensions of the bonds forming and breaking in the UCK2 reaction. The PES is generated by the adiabatic mapping approach,^48,49 incrementally stepping along the P–O bonds and optimizing the geometry of the system at each point with these two distances held fixed. This approach does not extensively sample different conformations of the surrounding enzyme and solvent, so that potential energies are calculated rather than free energies. The shape of the PES determines the mechanism of reaction and approximate location of the transition state, the exact location of which would be given by a smooth, fully continuous free energy surface. The QM/MM energies may be used to compute a predicted barrier to phosphate transfer for comparison to the experimental value. The mechanistic conclusions of this investigation add a new enzyme to the set of enzyme-catalyzed phosphate transfers for which mechanisms have been elucidated computationally. The results may also be used to help design PET probes or anticancer prodrugs to be activated by UCK2 based on 3′-C-ethynylcytidine and 3′-C-ethynyluridine.⁷

Results and discussion

UCK2 potential energy surface, minimum energy path, and mechanism

As mentioned in the Introduction, previous QM/MM studies on similar systems to UCK2 have concluded that the mechanisms can be associative,^36–39 dissociative,^40,41 or concerted.^31,42–47 One example from each of these possibilities is given in Table 1 to serve as reference points for comparison with the UCK2 mechanism. In the associative mechanism the key structure is the phosphorane intermediate. The bond distances are 2.0 Å for the bond-breaking distance and 2.1Å for the bond-forming distance.³⁶ In the metaphosphate anion example, the bond-breaking distance is 3.16 Å , although the bond-forming distance is very close to being fully formed, at 1.81 Å.⁴⁰ The validity of this mechanism has been called into question based on methodological issues,⁵⁰ and empirical valence bond methods have been used to calculate an associative mechanism in the Ras and RasGAP systems with energies in agreement with experiment.^38,39 The parameters used in Table 1 are still an indication of the geometry of a QM/MM dissociative transition state, and thus the region of the PES to explore in this study. In the concerted mechanism the bond-breaking distance is 2.32 Å, and the bond-forming distance is 2.12 Å.⁴²

Table 1.

Examples from previous QM/MM work demonstrating phosphate transfer or hydrolysis by an associative,³⁶ dissociative,⁴⁰ or concerted mechanism⁴²

Enzyme	Mechanism	Key Structure	Bond-Breaking Distance (Å)a	Bond-Forming Distance (Å)a
DNA Polymerase β36	Associative		2.0	2.1
Ras40	Dissociative		3.16	1.81
cAMP-Dependent Protein Kinase (PKA)42	Concerted		2.32	2.12

^aDistances are for the key structure.

The B3LYP/6–31G(d):AMBER potential energy surface of UCK2 was calculated with these distances as a guide, andis shown in Fig. 3. The surface is a function of the bond-forming Cyt 5′O–P distance that corresponds to the nucleophilic attack coordinate and the bond-breaking ATP O–P distance. The distances covered are from 1.9 Å to 2.5 Å in each coordinate, in 0.1 Å increments, for a total of 49 points on the PES, each scanned from multiple directions. The energies given are ONIOM energies^51,52 relative to the reactant structure optimized from the point with bond-forming distance 2.5 Å and bond-breaking distance 1.9 Å (Methods).

Fig. 3.

Potential energy surface for the reaction catalyzed by UCK2. Labels correspond to the transition state (TS), reactant basin (R), and product basin (P) on the surface.

The transition structure from this surface represents a concerted mechanism, with a bond-forming distance of 2.3 Å and a bond-breaking distance of 2.2 Å. This mechanism is in agreement with much,^31,42–47 although not all,^36–41 previous QM/MM work on similar systems. It is also the same mechanism as that given for the closest analog in the Mechanism, Annotation and Classification in Enzymes (MACiE) database, adenosine kinase (EC 2.7.1.20, MACiE entry M0209).⁵³ The bond distances are slightly different from those calculated for the PKA enzyme, given in Table 1, with the UCK2 transition state occurring earlier along the reaction coordinate with a longer bond-forming distance and a shorter bond-breaking distance.

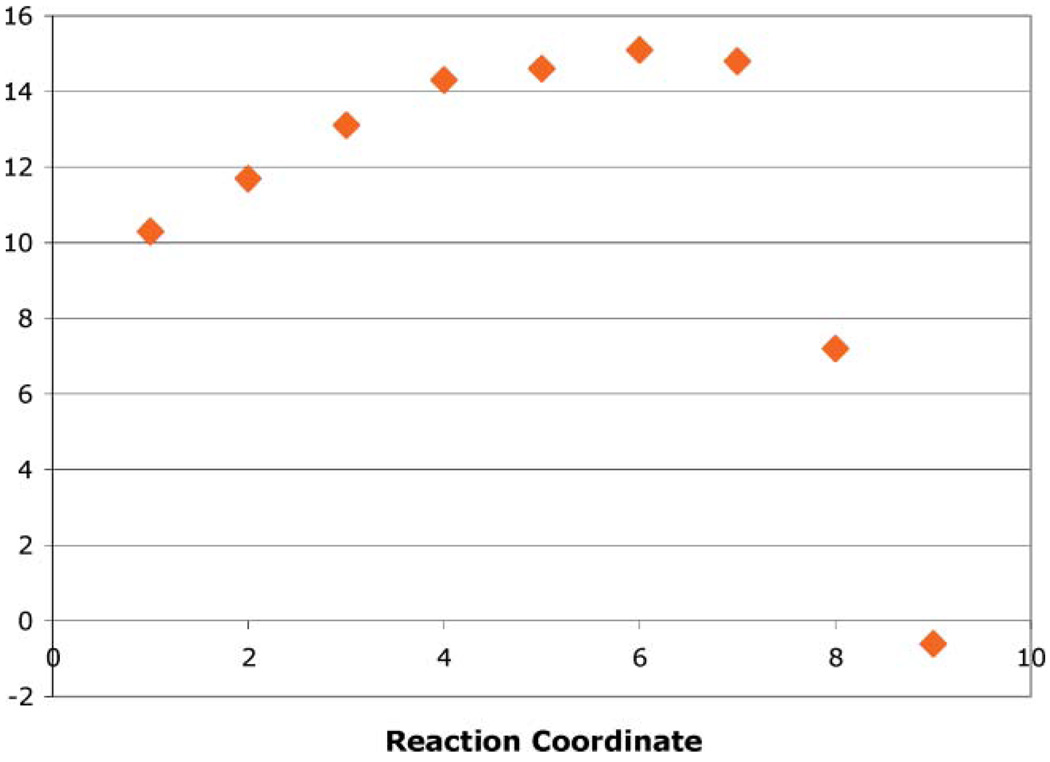
A 1D minimum energy path was created from the PES starting from the lowest energy point on the reactant side—the point with bond-forming distance 2.5 Å, bond-breaking distance 1.9 Å— and proceeding towards the product side via the lowest energy point obtained by either shortening the bond-forming distance by 0.1 Å, lengthening the bond-breaking distance by 0.1 Å, or both. This minimum energy path is shown in Fig. 4. The highest energy point along it is 15.1 kcal/mol relative to the reactant state. This represents the calculated barrier to the reaction. The experimental kinetic values measured for UCK2 catalysis of phosphate transfer to cytidine are a k_cat/K_m value of 3.7 × 10⁴ s⁻¹ M⁻¹ and a K_m of 8.6 × 10⁻⁵ M.¹¹ These give a k_cat of 3.2 s⁻¹, which corresponds to an experimental barrier of 17.5 kcal/mol using a temperature of 310K.⁵⁴

Fig. 4.

1D minimum energy path along the reaction coordinate. Reaction coordinate points are numbered sequentially from reactant to product sides.

The calculated barrier is lower than the experimental one by 2.4 kcal/mol, in comparable agreement with previously calculated reactions of this type when experimental barriers were compared to computed barriers.^{31,36,38,39,42,46,47} In some previous cases the calculated barrier was much lower than the experimental barrier, but this was suggested to be because chemistry was not rate-limiting.^37,44 This maybethe case for UCK2, which is characterized by a conformational change upon ligand binding that may be rate-determining,¹⁰ but the calculated barrier should still be close to experiment as was found here, since there is no evolutionary drive to optimize the chemical reaction by orders of magnitude over a conformational isomerization step.⁵⁵ QM/MM barriers can be affected in unpredictable ways by the starting structure,⁵⁶ QM method,⁴⁶ QM system size,⁴² boundary treatment,⁵⁷ and neglect or inclusion of free energy contributions,³⁷ among others.⁵⁰ While the numerical agreement with experiment may thus be partly fortuitous, the mechanistic conclusions are likely to be valid.³¹

Structures of the highest energy point on the 1D minimum energy path and the point immediately after it are shown in Fig. 5. In the highest energy point, and on the rest of the reactant side, the magnesium ion is coordinating with one of the carboxylate oxygens of Asp62, and the cytidine 5′O is protonated. In the next point, the bond-forming distance is shorter and the bond-breaking distance is longer, both by 0.1 Å. At this geometry and on the rest of the product side the lowest-energy structures have the magnesium ion coordinating with the ATP β-phosphate oxygen that breaks its bond with the ATP γ-phosphorus, and Asp62 is protonated.

Fig. 5.

Concerted transition state of UCK2 phosphate transfer. The highest energy point along the minimum energy path is the calculated transition structure, shown in (a), and the point immediately after it is shown in (b). Distances are in Ångstroms.

The reaction coordinates scanned were just the breaking and forming O–P bond lengths. The results suggest the transition state involves additional bonding changes, in particular proton transfer and magnesium ion coordination change, creating the slight discontinuity in Fig. 4. Similar transition states characterized by a single barrier for both a phosphate transfer and proton transfer reaction have been found before in similar systems,^{31,42,43,45,47} and the proposed role of Asp62 as a catalytic base has been confirmed by the theoretical studies here.¹⁰ This is also in agreement with the conservation of this residue among most kinases of UCK2’s type.¹⁰

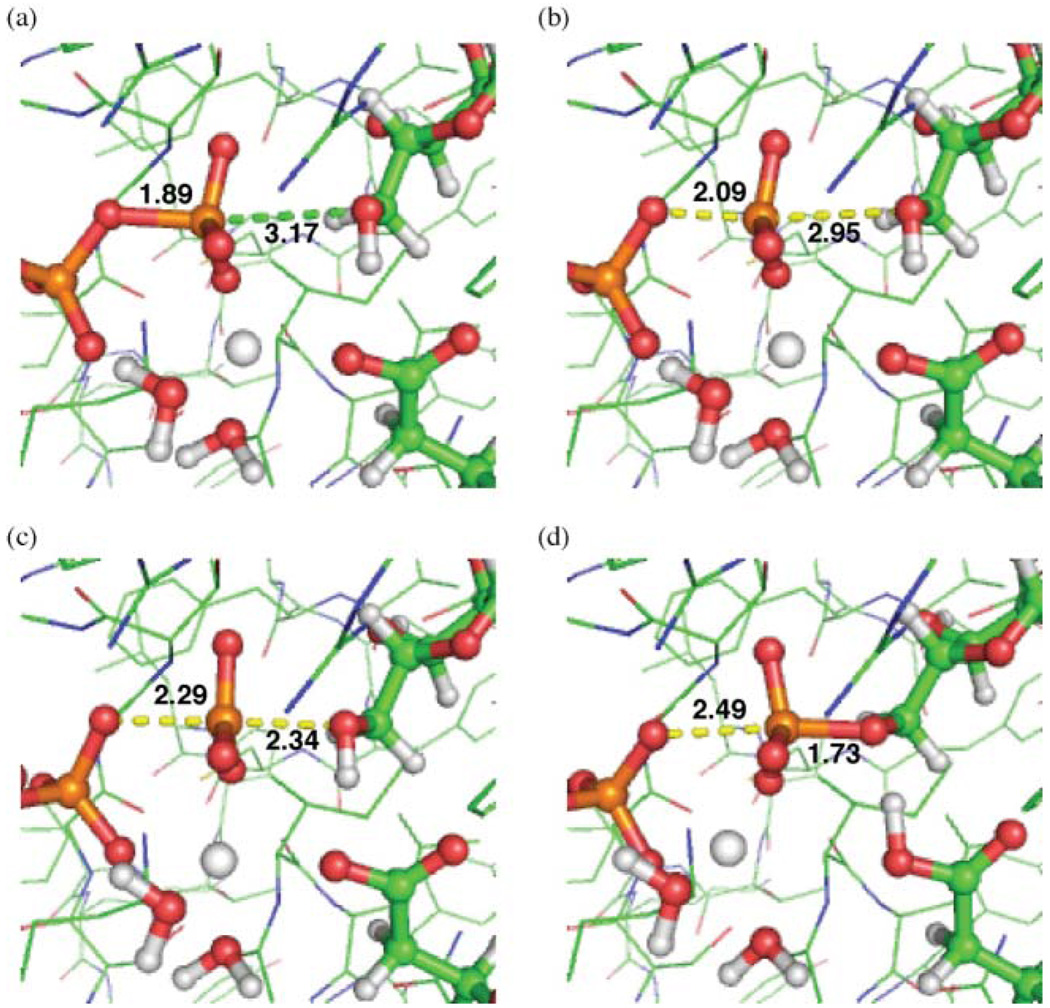
The PES covers regions off the minimum energy path, which affords insight into alternative mechanisms. There is no evidence for a stable phosphorane intermediate, which would have bond distances both around 2.0 and 2.1 Å as shown in Table 1.³⁶ The energy also appears to be rising in the region of a fully dissociated metaphosphate, but this PES only covers distances up to 2.5 Å, whereas in previous work the bond-breaking distance has been 3.1–3.2 Å (Table 1).^40,41 The transition state for metaphosphate formation should still be on this PES according to previous work;^40,41 in order to investigate this possibility, a scan of the bond-breaking distance was performed starting from the reactant structure with the bond-forming distance unconstrained and thus allowed to optimize to its lowest-energy position. This scan got caught in a loop between QM and MM calculations (Methods), but the data were enough to show that a dissociative mechanism is unlikely. Three optimized structures from this scan, and the final point before the calculation was trapped in a loop, are shown in Fig. 6. The energies of these geometries relative to the reactant are 5.5, 15.2, 19.2, and 9.4 kcal/mol (Fig. 6a,b,c,d). The cytidine 5′O forms a bond with the transferred phosphate when the breaking-bond distance is extended to 2.49 Å. This is considerably before it could become a stable, separate metaphosphate anion with a distance >3.0 Å (Table 1). Expansion of the potential energy surface could still provide evidence of a stable metaphosphate anion, but the transition state to its formation would have to be greater than 19.2 kcal/mol and could be significantly higher. This makes the dissociative mechanism an unlikely candidate for this enzyme.

Fig. 6.

Examination of dissociative mechanism. Geometries are from a scan of the bond-breaking coordinate starting at the reactant state. Distances are in Ångstroms. Points (a–c) were optimized with the bond-breaking distance frozen. Point (d) was the last point before the calculation failed, but it occurs after proton transfer and cytidine phosphate bond formation. Energies relative to the reactant are: (a) 5.5 kcal/mol, (b) 15.2 kcal/mol, (c) 19.2 kcal/mol, (d) 9.4 kcal/mol.

Comparisons of calculated reactant and TS to crystal structure, and potential for substrate design

The UCK2 reaction path was calculated in part to provide insight into the design of substrates to be phosphorylated by this enzyme for use as potential anticancer prodrugs or PET reporter probes for this enzyme. One approach to these could be similar to rational, structure-based drug design.⁵⁸ In structure-based drug design, the crystal structure of a bound ligand–protein complex is used to perform docking studies to calculate functional group modifications that will increase the binding affinity. In the case of substrate design, putative transition states of a large library of analogues may be virtually screened under the assumption that the molecules that interact most favorably with the enzyme will have the highest probability of undergoing the phosphorylation reaction.^59,60 A molecular mechanics docking score is not a surrogate for a reaction barrier, which would still require QM/MM evaluation by the methods used here, but might provide a fast way to evaluate a large set of molecules. The use of transition state models in this manner has been shown to improve substrate identification over the use of ground states in amidohydrolases,⁶¹ and was recently used to assign function to a protein of known structure but whose catalyzed reaction was unknown.⁶² In these previous studies, however, the geometries of the proteins were taken directly from crystal structures. In order to investigate whether different results might be obtained by using the protein in a transition state geometry, substrate/protein interactions in the calculated TS and reactant states of the UCK2 enzyme were compared to those in the crystal structure of the product state, which represents the alternative possibility for docking. The Ca RMSD of the TS from the crystal is 0.35 Å, the reactant from the crystal is 0.36 Å, and the TS from the reactant is 0.07 Å.

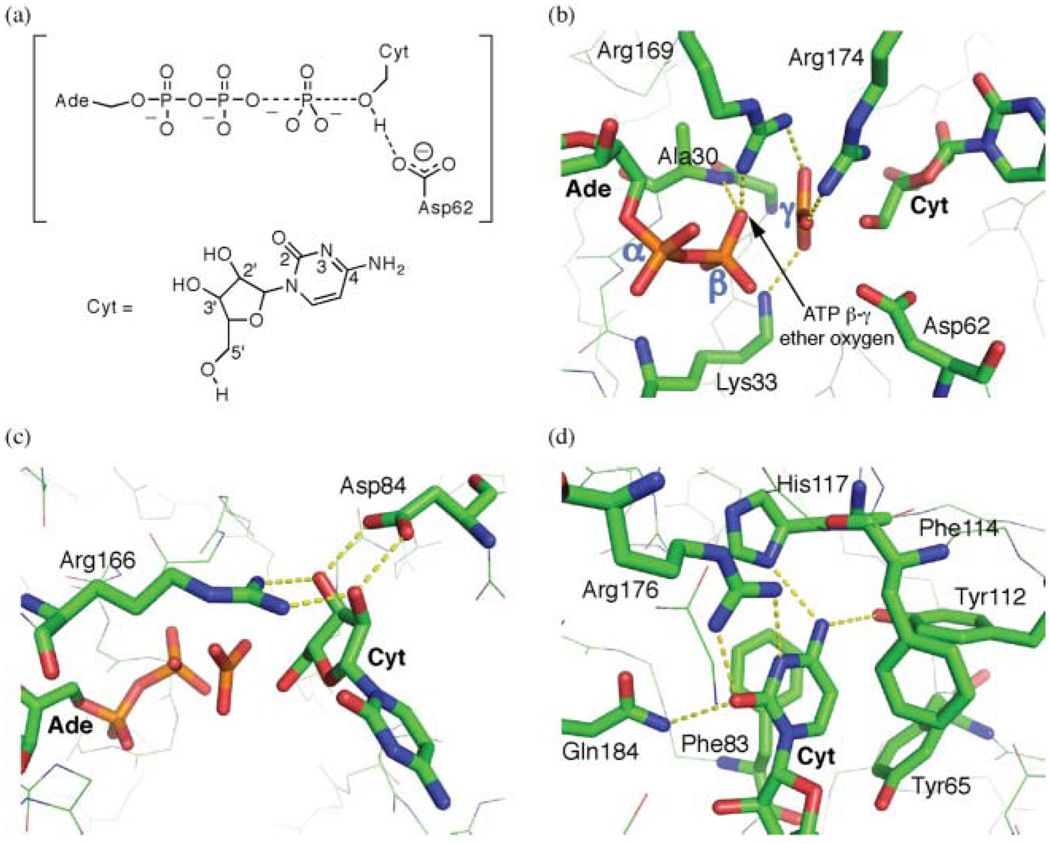
Hydrogen bond interactions between UCK2 and the transferring phosphate group oxygens are important for transition state stabilization. These include hydrogen bond donation from Lys33, Arg169, and Arg174 sidechains, as well as the backbone amide nitrogen of Ala30 (Fig. 7b). Differences in the catalytic site between the experimental (product) and calculated (reactant and transition state) structures are minimal (Table 2). Most parameters vary little, although the arginine hydrogen bonding distances are longer in the crystal structure of the product state than in the calculated reactant and transition states. In the case of Arg169, in the product state the two oxygens to which it is hydrogen bonding are separated by a greater distance than in the reactant and transition states as a result of the covalent bond cleavage. The guanidinium bridges a greater distance, and each hydrogen bond is lengthened as a result. In the case of Arg174, in the product state its approach to the oxygen to which it is hydrogen bonded becomes more sterically hindered as a result of covalent bond formation. This lengthens the donor–acceptor distance.

Fig. 7.

Interactions between UCK2 and the substrate in the transition state of the phosphate transfer reaction (a, with cytidine numbering). Dashes represent hydrogen bond interactions tabulated in Table 2 in the reactant, transition, and product states. Interactions between UCK2 and the oxygens that are bonded to the ATP γ-phosphorus in the reactant state are shown in (b). The ribose ring specificity dictated by Arg166 and Asp84 is shown in (c). Panel (d) shows the region around the pyrimidine ring of the cytidine (Cyt).

Table 2.

Hydrogen bond distances for interactions between UCK2 and the substrate in reactant, TS, and product states

		Hydrogen bond distance (heavy atom to heavy atom, Å)
Substrate Interaction Site	Hydrogen bond parameter	Reactant (calculated)	TS (calculated)	Product (crystal)
AT P γ-phosphate oxygens	Lys33–ATP γ-phosphate O	2.91	2.84	2.84
	Ala30–ATP β-γ ether O	2.77	2.74	2.92
	Arg169–ATP β-γ ether O	2.83	2.72	3.15
	Arg169–ATP γ-phosphate O	2.82	2.76	3.29
	Arg174–ATP γ-phosphate O	2.87	3.20	3.70
Cyt ribose 2′OH and 3′OH	Arg166–2′O	2.81	2.81	2.90
	Arg166–3′O	3.09	2.89	2.83
	Asp84-2′O	2.62	2.64	2.65
	Asp84-3′O	2.71	2.58	2.53
Cyt pyrimidine ring	His117–CytN4	2.89	2.92	2.90
	Tyr112–CytN4	2.95	2.96	2.82
	Arg176–CytO2	2.79	2.80	2.91
	Gln184–CytO2	3.06	3.27	3.26
	Arg176–CytN3	3.02	3.00	3.01

The UCK enzymes have high specificity for ribonucleosides over 2′-deoxyribonucleosides.^11,63 This is because the 2′- and 3′-hydroxyl groups each accept a hydrogen bond from Arg166 while donating one each to Asp84 (Fig. 7c).¹⁰ This specificity may be used to the advantage of therapeutic or imaging substrate design in the use of the ribose ring as a binding handle for the introduction of nucleosides with substitutions on the pyrimidine ring. These parameters also change very little throughout the course of the reaction (Table 2).

The cytosine base exhibits numerous interactions with the UCK2 enzyme (Fig. 7d).¹⁰ The amine N4 atom donates hydrogen bonds to His117 and Tyr112, while the carbonyl O2 accepts hydrogen bonds from Arg176 and, slightly more distantly, Gln184. The N3 atom of the pyrimidine ring also accepts a hydrogen bond from Arg176. Additional aromatic interactions are observed in the form of π-stacking with Phe83, cytosine edge-to-face interaction with Tyr65, and face-to-edge with Phe114. The hydrogen bonds were maintained throughout the reaction (Table 2). The aromatic interactions also appear qualitatively conserved.

In the UCK2 kinase enzyme the reacting region is the transferred phosphate and the atoms closely connected to it. These are relatively distant from the pyrimidine ring, which would be used to confer specificity in the design of substrates for this enzyme. While the preferential stabilization of transition states by enzymes suggests that the TS would be the best choice for docking if a large library is to be screened,⁶⁴ substrate–protein interactions of substituents on the ring would not differ much in the reactant, transition state, and product states (Fig. 7d, Table 2). This implies that initial virtual screening could be performed with any of these states, although barriers should still be evaluated by QM/MM methods as used here, with molecular dynamics to accommodate the substituent groups in the binding pocket. The mechanistic conclusions and transition state geometry calculated for the UCK2 phosphorylation of cytidine will aid in future reaction path determination and barrier calculation of alternative substrates for this enzyme.

Alternatively, a UCK2 mutant enzyme may be rationally designed to stabilize a QM/MM-based transition state for a non-natural nucleoside. Computational stabilization of QM transition state models has been used to design new enzymes to catalyze a Kemp elimination⁶⁵ and retroaldol reaction.⁶⁶ These methods could also model the effects of mutations in the design of bulkier substrates that would be poorly phosphorylated by native UCK2, redesigning the natural enzyme to be a better PET reporter. A transition state model was recently used in this way to rationally redesign a carbonic anhydrase enzyme into a benzoate ester hydrolase.⁶⁷

Experimental

System preparation and MM molecular dynamics equilibration of water

The computational model for the UCK2 system was taken from a crystal structure of UCK2 complexed with the products ADP and CMP (Protein Data Bank code 1UJ2).¹⁰ The biological unit of UCK2 is a homotetramer, and the crystal structure is a dimer. To reduce the system size for greater computational tractability, one monomer was chosen for simulation, chain A, and the other monomer, chain B, was deleted. The closest atom from chain B to any of the atoms on the chain A ADP β-phosphate, CMP α-phosphate, or magnesium ion was 16.15 Å away in the crystal structure, indicating that any direct effect on the mechanism and barrier calculated here should be minimal.

Molecular mechanics calculations were carried out with the AMBER suite of programs to solvate and equilibrate the system before QM/MM.⁶⁸ The protonation states of ADP and CMP were chosen to be ADP³⁻ and CMP²⁻, making the reactant ATP⁴⁻ as shown in Fig. 1. The pK_a of H(ATP)³⁻ in water is 6.47, meaning that at physiological pH 7.4 free ATP in solution is 89% ATP⁴⁻ and 11% H(ATP)³⁻, with the proton on the γ-phosphate.^69,70 This ratio is enhanced by complexation with Mg²⁺, in which the pK_a is 4.60 and the population at pH 7.4 is 99.8% Mg(ATP)²⁻ and 0.2% Mg(H·ATP)⁻.^69,70 Finally, the phosphate oxygens in the crystal structure appear to be only hydrogen bond acceptors and not hydrogen bond donors. The parameters for ADP³⁻ were taken from Meagher, Redman, and Carlson.⁷¹ For CMP²⁻ the phosphate atom types and internal coordinate parameters were taken from the same reference, while the charges were generated analogously. Methyl monophosphate was optimized quantum mechanically by HF/6-31+G(d) using the Gaussian03 program.⁷² RESP charges were calculated⁷³ with the total charge on the methyl group restrained to be +0.19e to allow incorporation onto the existing AMBER RC3 nucleotide. RC3 is identical to CMP in every way except that it has one less oxygen on its 5′-phosphate (this oxygen would normally be the 3′O of the neighboring nucleotide). All of the non-methoxy oxygens were constrained to have the same charge during the RESP calculations. An AMBER CMP residue was created with atom types and internal coordinate parameters from RC3 and Meagher, Redman, and Carlson,⁷¹ charges from RC3onthe nucleotide sugar and base, and charges from the methyl monophosphate RESP calculations on the phosphate group.

The rest of the protonation states were chosen based on the results of a PropKa calculation (http://propka.ki.ku.dk/~drogers/) with the exception of the active site aspartic acid, Asp62. In the crystal structure it appears to be a hydrogen bond donor to the CMP phosphoester oxygen, indicating it should be protonated. The pK_a predicted by PropKa for this residue was elevated to 7.25, suggesting it could be protonated at physiological pH. It was set as the AMBER residue ASH, for a protonated aspartic acid. Hydrogen atoms were added to the crystal structure using the LEaP program of the AMBER suite, and parameters were assigned according to the Amber ff99 force field.^68,74 Seven sodium counterions were added to neutralize the system. A truncated octahedral box of TIP3P waters was added with a 15 Å buffer around the protein.⁷⁵ The final system consisted of 3,500 protein atoms, 1 Mg²⁺ ion, 7 Na⁺ ions, and 40,518 water atoms for a total of 44,026 atoms.

The molecular mechanics calculations were focused on equilibrating the waters, with the protein kept relatively fixed to its crystal geometry to minimize any artificial rearrangements due to the truncation of the system to a single monomer. Minimizations and dynamics were run using the SANDER module of the AMBER suite.⁶⁸ First, the system was minimized with restraints of 20.0 kcal/(mol Ų) on the protein heavy atoms and magnesium ion. Constant volume molecular dynamics (MD) simulations were then run for 50 ps at 100K followed by constant pressure dynamics for 50 ps at 100K to ensure the density reached ~0.99 g/cm³. In these 100 ps of MD only the waters were free to move. Then constant volume MD was run with 2.0 kcal/(mol Ų) restraints on the protein heavy atoms and magnesium, and the system was gradually heated from 100K to 298K over 50 ps, at which it remained for 200 ps before cooling back to 100K over 50 ps. Finally the system was minimized free of all restraints. After the final minimization, an AMBER restart file was created using the Ptraj program of AMBER⁶⁸ with all molecules imaged to be in one primary periodic box unit cell.

QM/MM calculations by ONIOM method

Morokuma et al.’s “our Own N-layer Integrated molecular Orbital molecular Mechanics” (ONIOM) method^51,52 was used for QM/MM calculationsas implemented in Gaussian03.⁷² In this method the system is multiplied into three parts: a whole system whose energy is evaluated molecular mechanically, a smaller model system whose energy is evaluated quantum mechanically, and the same model system but with the energy evaluated molecular mechanically. The whole system is also referred to as the “real” system.^51,52 The total ONIOM energy is evaluated by the following equation:

$${\mathrm{E}}_{\text{ONIOM}}={{\mathrm{E}}^{\text{whole}}}_{\text{MM}}+{{\mathrm{E}}^{\text{model}}}_{\text{QM}}-{{\mathrm{E}}^{\text{model}}}_{\text{MM}}$$ (1)

For UCK2, the model system was chosen to include the Asp62 carboxylic acid and β-carbon methylene group, the magnesium ion and two coordinating waters, the CMP phosphate PO₃²⁻, 5′O, 5′CH₂, and 4′CH, the ADP α- and β-phosphate groups, 5′O, and 5′CH₂, and the hydroxymethylene moiety of Ser34, which was coordinating with the Mg²⁺ in the crystal structure but not in the minimized structure after water equilibration (Fig. 8). The whole, or “real”, system included all protein atoms, ions, and all waters with any atom within 15 Å of one of the QM model atoms in the minimized structure. The empty valences of the model system, which are covalent bonds in the whole system, were filled by hydrogen atoms in the link atom approach.⁷⁶

Fig. 8.

QM/MM partition of UCK2 system. Atoms shown in spheres and sticks make up the model system, whose energy is evaluated with both quantum mechanics and molecular mechanics in ONIOM. Atoms represented as lines are modeled by MM only, but can polarize the QM wavefunction as point charges. The geometry comes from the final minimized structure after MM equilibration of waters. Hydrogens and non-QM waters are hidden for clarity.

A Perl script was written to create a Gaussian03 input file from the output of the AMBER calculations. Protein atoms within 10 Å of the QM model system, and water residues with any atom within 10 Å of the QM model system were allowed to move during the QM/MM calculations along with the model system itself. All other atoms were frozen. The QM method used was the hybrid density functional theory B3LYP method^77,78 with the 6–31G(d) basis set, while the AMBER force field was used for the MM energies. The QM wavefunction was allowed to be polarized by the MM point charges using electronic embedding.⁵¹ The PES was generated by scans along the bonds forming and breaking in increments of 0.1 Å with loose convergence criteria. The PES was scanned from multiple directions in order to smooth out any discontinuities, with the final PES determined by the lowest energy found for each point.³¹ During electronic embedding calculations the QM wavefunction is calculated with a fixed model system, point charges are determined from that wavefunction, and the whole MM system is then minimized with frozen model system coordinates.^51,52 After this, the QM wavefunction is calculated again, point charges determined, and the MM system is then re-optimized with the new point charges.^51,52 In some instances this can lead to the calculation getting caught in a loop where one QM wavefunction will lead to one MM geometry, but the QM wavefunction calculated from this structure then leads to a different MM geometry, which then gives the first QM wavefunction, then the first MM structure, and so the calculation cycles in a sequence of QM_a → MM_a → QM_b → MM_b → QM_a → MM_a and so on, all with frozen model system coordinates. This problem occurs most commonly when mobile waters oscillate between hydrogen bond acceptors. The scans from multiple directions also helped to give energies for points that were caught in these loops. This issue of loops could be eliminated by calculations using mechanical embedding, in which the QM model system is not polarized by the surrounding MM atoms, but this is a less accurate representation of the true reaction.⁵¹ In theory this could be made up for with a large enough QM model system including residues directly interacting with the reacting region as well as a secondary shell of residues that might polarize the primary shell, but in the UCK2 system with a large number of hydrogen bond acceptors and donors this was not feasible. The reactant was determined by a full, unconstrained optimization from a point on the reactant side of the PES using default convergence criteria.

Direct TS searches were attempted but failed to converge for methodological reasons; these involve the Hessian being made up of only the model system coordinates rather than the whole system and the generally poor quality of the Hessian, which is updated using QM forces only.⁷⁹ Work is underway in developing a method that can perform direct TS searches within the ONIOM framework, but it is only applicable to the mechanical embedding scheme and only available in the private development version of Gaussian.^79,80

Conclusions

Combined QM/MM calculations with B3LYP/6–31G(d): AMBER have been performed on the UCK2 enzyme and shown that the phosphate transfer reaction proceeds through a concerted mechanism with a single transition state. The 2D potential energy surface gives a transition state geometry with a bond-forming distance of 2.3 Å and a bond-breaking distance of 2.2 Å. The reaction coordinate includes contributions from breaking and forming the phosphate bonds, the proton transfer from the cytidine 5′-hydroxy group to the catalytic base Asp62, and a change in magnesium ion position to coordinate with the oxygen that is liberated after breaking the ATP γ-phosphate bond.

The calculated barrier for this reaction is 15.1 kcal/mol, in reasonable agreement with the experimental barrier of 17.5 kcal/mol.¹¹ While the calculated barrier may change depending on the simulation parameters, the mechanism is expected to remain valid. This is the first QM/MM study of UCK2, but previous QM/MM studies of enzyme-catalyzed phosphate transfer and hydrolysis have proven that these reactions do not follow a single mechanism.^31,36–47 Examples of stable pentavalent phosphorane^36–39 or metaphosphate anions^40,41 have been found in some cases. Both of these alternative mechanisms have been explored and found not to occur in UCK2.

The structures of the reactant, transition state, and product state maintain qualitatively similar, although not identical, interactions. Future calculations and experimental work will be directed toward the design of efficient and specific anticancer drugs or PET reporter probes for this non-immunogenic candidate reporter enzyme.