Abstract
In both ionic components of the title salt, C4H7N2 +·C6H2N3O7 −, the rings are approximately planar; the maximum deviation from the mean plane is an order of magnitude larger in the picrate ring [0.0289 (10) Å] than in the imidazolium ring [0.0028 (10) Å. The nitro groups are twisted with respect to the six-atom ring plane; the NO2 groups next to the oxide O atom, at the 2- and 6-positions, are twisted more [by 53.59 (9) and 18.46 (12)°] than the NO2 group at the 4-postition, for which the twist angle is 7.28 (16)°. In the crystal, N—H⋯O hydrogen bonds, in which the hydroxyl O atom acts as a double acceptor and one of the O atoms from a nitro group acts as an additional acceptor, connect molecules into chains along the c-axis direction. Relatively short C—H⋯O contacts and π–π interactions between symmetry-related six-membered rings [centroid–centroid distances = 3.5938 (10) and 3.6223 (10) Å] also occur.
Related literature
For the crystal structure of imidazolium picrate, see: Soriano-García et al. (1990 ▶). For the structures of picrates of some other imidazole derivatives, see, for example: Nardelli et al. (1987 ▶); Du & Zhao (2003 ▶); MacDonald et al. (2005 ▶); Pi et al. (2009 ▶).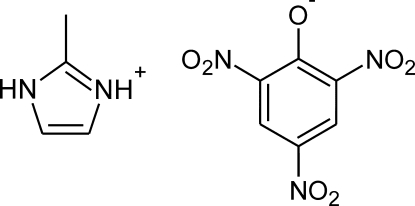
Experimental
Crystal data
C4H7N2 +·C6H2N3O7 −
M r = 311.22
Monoclinic,
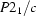
a = 7.0983 (9) Å
b = 21.644 (2) Å
c = 8.1583 (9) Å
β = 100.327 (12)°
V = 1233.1 (2) Å3
Z = 4
Mo Kα radiation
μ = 0.15 mm−1
T = 295 K
0.3 × 0.2 × 0.2 mm
Data collection
Oxford Diffraction Xcalibur Eos diffractometer
Absorption correction: multi-scan (CrysAlis PRO; Oxford Diffraction, 2009 ▶) T min = 0.964, T max = 1.000
4778 measured reflections
2483 independent reflections
1792 reflections with I > 2σ(I)
R int = 0.014
Refinement
R[F 2 > 2σ(F 2)] = 0.039
wR(F 2) = 0.101
S = 1.03
2483 reflections
235 parameters
All H-atom parameters refined
Δρmax = 0.30 e Å−3
Δρmin = −0.27 e Å−3
Data collection: CrysAlis PRO (Oxford Diffraction, 2009 ▶); cell refinement: CrysAlis PRO; data reduction: CrysAlis PRO; program(s) used to solve structure: SIR92 (Altomare et al., 1993 ▶); program(s) used to refine structure: SHELXL97 (Sheldrick, 2008 ▶); molecular graphics: Stereochemical Workstation Operation Manual. (Siemens, 1989 ▶); software used to prepare material for publication: SHELXL97.
Supplementary Material
Crystal structure: contains datablocks I, global. DOI: 10.1107/S1600536810053390/dn2638sup1.cif
Structure factors: contains datablocks I. DOI: 10.1107/S1600536810053390/dn2638Isup2.hkl
Additional supplementary materials: crystallographic information; 3D view; checkCIF report
Table 1. Hydrogen-bond geometry (Å, °).
| D—H⋯A | D—H | H⋯A | D⋯A | D—H⋯A |
|---|---|---|---|---|
| C5—H5⋯O21i | 0.911 (19) | 2.478 (19) | 3.378 (2) | 169.4 (16) |
| N11—H11⋯O1 | 0.89 (2) | 1.95 (2) | 2.8357 (19) | 172.9 (19) |
| N13—H13⋯O1ii | 0.86 (2) | 2.09 (2) | 2.819 (2) | 143 (2) |
| N13—H13⋯O22ii | 0.86 (2) | 2.14 (2) | 2.782 (2) | 131.3 (19) |
Symmetry codes: (i) 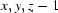 ; (ii)
; (ii) 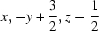 .
.
Acknowledgments
SS thanks Mangalore University for the research facilities
supplementary crystallographic information
Comment
The imidazole nucleus appears in a number of naturally occurring products like amino acid histidine and purines which comprise many of the most important bases in nucleic acids. Imidazole derivatives deal with a broad spectrum of pharmacological activities. The crystal structures of some imidazolium picrates have been reported, for instance imidazolium picrate itself (Soriano-García et al. (1990); also two solvates (hydrate and ethanolate) of 2-aminohistamine dipicrate (Nardelli et al.,1987), 4-hydroxymethylimidazolium picrate (Du & Zhao, 2003), two polymorphs of betaine bis(diimidazolium) dipicrate (MacDonald et al., 2005) and 3-benzyl-1-methyl-imidazolium picrate (Pi et al., 2009).
The title compound, 2-methylimidazolium picrate (2-methyl-1H-imidazol-3-ium 2,4,6-trinitrophenolate, Scheme 1) crystallizes with two ionic components, as proved by successful location and refinement of hydrogen atoms at both imiadzole nitrogen atoms as well as by the bond length pattern. Both cyclic fragments are in a good approximation planar. As might be expected, the deviations from the least-squares plane are by an order of magnitude smaller in the imidazolium ring (maximum 0.0028 (10) Å) than in a six-atom ring of picrate anion (0.0289 (10) Å). The two rings make a dihedral angle of 60.28 (7)°. The nitro groups are twisted with respect to the ring plane; the dihedral angles are larger for the substituents ortho- with respect to the C=O- group (18.46 (12)° and 53.59 (9)°) than for the para-group, which is 7.28 (16)°.
The ionic fragments are conneced by relatively short N—H···O hydrogen bonds. One of N—H groups acts as a donor in almost linear hydrogen bond, while the other is involved in the bifurcated N—H···O bonds, in which O1 atom and one of nitro group O atoms act as acceptors. These two bonds are of similar lengths and therefore they deviate significantly from linearity. These hydrogen bonds, together with relatively short C—H···O contacts connect the cations and anions into a layer in which one can find the C12(6) chains, created only by N—H···O hydrogen bonds and R45(21) rings, in which all contacts are involved (Fig. 2).
The layers related by centers of symmetry are additionally connected by quite short π–π stacking interactions between six-membered rings. The distances between the centers of consecutive rings in a stack are 3.594Å and 3.621Å, but if the parallel shift is taken into account the distances between the planes are 3.48Å and 3.27Å (Fig. 3). It should be noted, however, that the parallel shift is in these cases 1.00Å and 1.50Å, respectively, which might suggest weak π–π stacking in the first case but edge-to-edge kind of interaction in the second.
Experimental
2-Methyl imidazole (0.82 g, 0.01 mol) was dissolved in 25 ml of ethanol. Picric acid (2.29 g, 0.01 mol) was dissolved in 15 ml of water. Both the solutions were mixed and to this, 5 ml of 5M HCl was added and stirred for few minutes. The formed complex (I) was filtered and dried. Good quality crystals were grown from ethanol solution by slow evaporation (m. p.: 483 K). Composition: Found (Calculated): C: 38.50 (38.59); H: 2.88 (2.91); N: 22.45 (22.50).
Refinement
Hydrogen atoms were located in difference Fourier maps and isotropically refined.
Figures
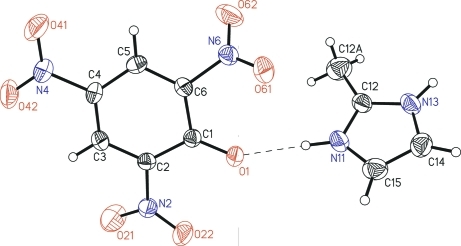
Fig. 1.
Anisotropic ellipsoid representation of the compound I together with atom labelling scheme. The ellipsoids are drawn at the 50% probability level, hydrogen atoms are depicted as spheres with arbitrary radii; hydrogen bond is shown as dashed line/
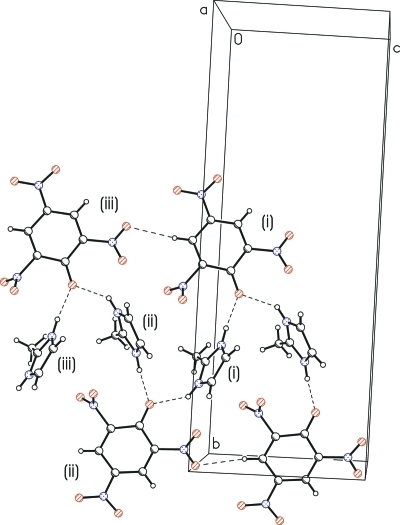
Fig. 2.
The layer of molecules of I as seen approximately along x direction; hydrogen bonds are shown as dashed lines. Syzmmetry codes: (i) x,3/2 - y,-1/2 + z; (ii) x,y,-1 + z; (iii) x,3/2 - y,-3/2 + z.
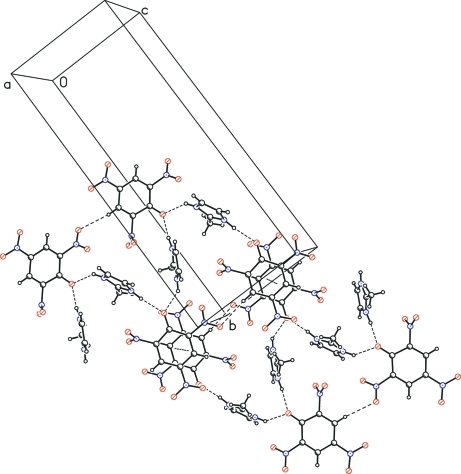
Fig. 3.
Two layers related by the center of symmetry; hydrogen bonds and π–π contacts are shown as dashed lines.
Crystal data
| C4H7N2+·C6H2N3O7− | F(000) = 640 |
| Mr = 311.22 | Dx = 1.676 Mg m−3 |
| Monoclinic, P21/c | Mo Kα radiation, λ = 0.71073 Å |
| Hall symbol: -P 2ybc | Cell parameters from 2592 reflections |
| a = 7.0983 (9) Å | θ = 2.9–28.2° |
| b = 21.644 (2) Å | µ = 0.15 mm−1 |
| c = 8.1583 (9) Å | T = 295 K |
| β = 100.327 (12)° | Block, yellow |
| V = 1233.1 (2) Å3 | 0.3 × 0.2 × 0.2 mm |
| Z = 4 |
Data collection
| Oxford Diffraction Xcalibur Eos diffractometer | 2483 independent reflections |
| Radiation source: Enhance (Mo) X-ray Source | 1792 reflections with I > 2σ(I) |
| graphite | Rint = 0.014 |
| Detector resolution: 16.1544 pixels mm-1 | θmax = 28.2°, θmin = 2.9° |
| ω scans | h = −8→9 |
| Absorption correction: multi-scan (CrysAlis PRO; Oxford Diffraction, 2009) | k = −15→28 |
| Tmin = 0.964, Tmax = 1.000 | l = −10→10 |
| 4778 measured reflections |
Refinement
| Refinement on F2 | Primary atom site location: structure-invariant direct methods |
| Least-squares matrix: full | Secondary atom site location: difference Fourier map |
| R[F2 > 2σ(F2)] = 0.039 | Hydrogen site location: inferred from neighbouring sites |
| wR(F2) = 0.101 | All H-atom parameters refined |
| S = 1.03 | w = 1/[σ2(Fo2) + (0.060P)2] where P = (Fo2 + 2Fc2)/3 |
| 2483 reflections | (Δ/σ)max = 0.001 |
| 235 parameters | Δρmax = 0.30 e Å−3 |
| 0 restraints | Δρmin = −0.27 e Å−3 |
Special details
| Geometry. All e.s.d.'s (except the e.s.d. in the dihedral angle between two l.s. planes) are estimated using the full covariance matrix. The cell e.s.d.'s are taken into account individually in the estimation of e.s.d.'s in distances, angles and torsion angles; correlations between e.s.d.'s in cell parameters are only used when they are defined by crystal symmetry. An approximate (isotropic) treatment of cell e.s.d.'s is used for estimating e.s.d.'s involving l.s. planes. |
| Refinement. Refinement of F2 against ALL reflections. The weighted R-factor wR and goodness of fit S are based on F2, conventional R-factors R are based on F, with F set to zero for negative F2. The threshold expression of F2 > σ(F2) is used only for calculating R-factors(gt) etc. and is not relevant to the choice of reflections for refinement. R-factors based on F2 are statistically about twice as large as those based on F, and R- factors based on ALL data will be even larger. |
Fractional atomic coordinates and isotropic or equivalent isotropic displacement parameters (Å2)
| x | y | z | Uiso*/Ueq | ||
| C1 | 0.3265 (2) | 0.93118 (8) | 0.60988 (19) | 0.0241 (4) | |
| O1 | 0.38378 (17) | 0.88003 (5) | 0.67241 (14) | 0.0347 (3) | |
| C2 | 0.2787 (2) | 0.98440 (7) | 0.70037 (19) | 0.0253 (4) | |
| N2 | 0.2874 (2) | 0.98159 (7) | 0.88019 (17) | 0.0358 (4) | |
| O21 | 0.2016 (3) | 1.02077 (8) | 0.94412 (17) | 0.0716 (5) | |
| O22 | 0.3770 (3) | 0.94120 (7) | 0.96128 (17) | 0.0656 (5) | |
| C3 | 0.2171 (2) | 1.03981 (8) | 0.6272 (2) | 0.0266 (4) | |
| H3 | 0.189 (2) | 1.0723 (8) | 0.691 (2) | 0.028 (5)* | |
| C4 | 0.1956 (2) | 1.04630 (8) | 0.4569 (2) | 0.0267 (4) | |
| N4 | 0.1304 (2) | 1.10493 (7) | 0.38329 (19) | 0.0348 (4) | |
| O41 | 0.1247 (2) | 1.11171 (7) | 0.23347 (17) | 0.0615 (5) | |
| O42 | 0.08086 (19) | 1.14506 (6) | 0.47167 (17) | 0.0479 (4) | |
| C5 | 0.2260 (2) | 0.99677 (8) | 0.3565 (2) | 0.0272 (4) | |
| H5 | 0.205 (3) | 0.9999 (9) | 0.243 (2) | 0.041 (5)* | |
| C6 | 0.2876 (2) | 0.94228 (7) | 0.43176 (19) | 0.0248 (4) | |
| N6 | 0.3054 (2) | 0.89003 (7) | 0.32303 (17) | 0.0310 (3) | |
| O61 | 0.45451 (19) | 0.86075 (6) | 0.34477 (16) | 0.0436 (4) | |
| O62 | 0.1676 (2) | 0.87781 (7) | 0.21488 (17) | 0.0537 (4) | |
| N11 | 0.5304 (2) | 0.76346 (7) | 0.59823 (18) | 0.0353 (4) | |
| H11 | 0.491 (3) | 0.8016 (10) | 0.617 (3) | 0.054 (6)* | |
| C12 | 0.4264 (2) | 0.72364 (8) | 0.49579 (19) | 0.0310 (4) | |
| C12A | 0.2238 (3) | 0.73045 (13) | 0.4178 (3) | 0.0484 (5) | |
| H12A | 0.163 (5) | 0.6936 (15) | 0.401 (4) | 0.129 (13)* | |
| H12B | 0.155 (4) | 0.7574 (13) | 0.480 (3) | 0.094 (9)* | |
| H12C | 0.213 (4) | 0.7461 (14) | 0.318 (4) | 0.111 (11)* | |
| N13 | 0.5382 (2) | 0.67629 (7) | 0.47868 (18) | 0.0341 (4) | |
| H13 | 0.506 (3) | 0.6450 (11) | 0.416 (3) | 0.056 (7)* | |
| C14 | 0.7165 (3) | 0.68530 (9) | 0.5723 (2) | 0.0377 (4) | |
| H14 | 0.811 (3) | 0.6565 (10) | 0.574 (2) | 0.046 (6)* | |
| C15 | 0.7118 (3) | 0.74005 (9) | 0.6470 (2) | 0.0391 (5) | |
| H15 | 0.808 (3) | 0.7634 (10) | 0.719 (3) | 0.057 (6)* |
Atomic displacement parameters (Å2)
| U11 | U22 | U33 | U12 | U13 | U23 | |
| C1 | 0.0225 (7) | 0.0236 (9) | 0.0259 (8) | 0.0002 (7) | 0.0035 (6) | 0.0003 (7) |
| O1 | 0.0505 (7) | 0.0247 (7) | 0.0282 (6) | 0.0088 (6) | 0.0053 (5) | 0.0019 (5) |
| C2 | 0.0274 (8) | 0.0263 (9) | 0.0219 (8) | −0.0003 (7) | 0.0038 (6) | 0.0000 (7) |
| N2 | 0.0501 (9) | 0.0318 (9) | 0.0252 (7) | 0.0080 (7) | 0.0062 (7) | −0.0004 (7) |
| O21 | 0.1138 (13) | 0.0717 (12) | 0.0334 (7) | 0.0473 (10) | 0.0244 (8) | 0.0002 (8) |
| O22 | 0.1215 (14) | 0.0427 (9) | 0.0296 (7) | 0.0315 (9) | 0.0057 (8) | 0.0062 (7) |
| C3 | 0.0266 (8) | 0.0239 (9) | 0.0299 (9) | 0.0008 (7) | 0.0070 (7) | −0.0040 (8) |
| C4 | 0.0280 (8) | 0.0209 (9) | 0.0321 (9) | 0.0018 (7) | 0.0077 (7) | 0.0050 (7) |
| N4 | 0.0378 (8) | 0.0286 (9) | 0.0385 (8) | 0.0024 (7) | 0.0084 (7) | 0.0083 (7) |
| O41 | 0.1011 (12) | 0.0457 (9) | 0.0393 (8) | 0.0197 (8) | 0.0173 (8) | 0.0183 (7) |
| O42 | 0.0632 (9) | 0.0264 (7) | 0.0563 (9) | 0.0118 (6) | 0.0165 (7) | 0.0024 (7) |
| C5 | 0.0292 (8) | 0.0304 (10) | 0.0223 (8) | −0.0002 (7) | 0.0052 (7) | 0.0037 (8) |
| C6 | 0.0261 (8) | 0.0239 (9) | 0.0250 (8) | −0.0007 (7) | 0.0067 (6) | −0.0028 (7) |
| N6 | 0.0395 (8) | 0.0282 (8) | 0.0265 (7) | −0.0004 (7) | 0.0093 (6) | −0.0008 (6) |
| O61 | 0.0498 (8) | 0.0378 (8) | 0.0451 (8) | 0.0136 (7) | 0.0134 (6) | −0.0063 (6) |
| O62 | 0.0563 (8) | 0.0575 (10) | 0.0419 (8) | −0.0018 (7) | −0.0060 (7) | −0.0211 (7) |
| N11 | 0.0479 (9) | 0.0240 (8) | 0.0329 (8) | −0.0010 (8) | 0.0044 (7) | −0.0042 (7) |
| C12 | 0.0424 (10) | 0.0252 (9) | 0.0256 (8) | −0.0034 (8) | 0.0067 (7) | −0.0002 (7) |
| C12A | 0.0426 (12) | 0.0519 (15) | 0.0477 (12) | −0.0025 (11) | 0.0000 (10) | 0.0012 (12) |
| N13 | 0.0501 (9) | 0.0230 (8) | 0.0293 (8) | −0.0043 (7) | 0.0077 (7) | −0.0044 (7) |
| C14 | 0.0426 (11) | 0.0329 (11) | 0.0381 (10) | 0.0036 (9) | 0.0084 (9) | 0.0046 (9) |
| C15 | 0.0416 (10) | 0.0374 (12) | 0.0356 (10) | −0.0071 (9) | −0.0005 (8) | 0.0006 (9) |
Geometric parameters (Å, °)
| C1—O1 | 1.2557 (19) | N6—O61 | 1.2193 (18) |
| C1—C2 | 1.441 (2) | N6—O62 | 1.2226 (19) |
| C1—C6 | 1.450 (2) | N11—C12 | 1.329 (2) |
| C2—C3 | 1.376 (2) | N11—C15 | 1.375 (2) |
| C2—N2 | 1.459 (2) | N11—H11 | 0.89 (2) |
| N2—O22 | 1.2067 (19) | C12—N13 | 1.319 (2) |
| N2—O21 | 1.2145 (19) | C12—C12A | 1.472 (3) |
| C3—C4 | 1.377 (2) | C12A—H12A | 0.91 (3) |
| C3—H3 | 0.918 (18) | C12A—H12B | 0.96 (3) |
| C4—C5 | 1.389 (2) | C12A—H12C | 0.87 (3) |
| C4—N4 | 1.444 (2) | N13—C14 | 1.370 (2) |
| N4—O42 | 1.2200 (19) | N13—H13 | 0.86 (2) |
| N4—O41 | 1.2245 (19) | C14—C15 | 1.336 (3) |
| C5—C6 | 1.365 (2) | C14—H14 | 0.92 (2) |
| C5—H5 | 0.911 (19) | C15—H15 | 0.96 (2) |
| C6—N6 | 1.457 (2) | ||
| O1—C1—C2 | 125.83 (14) | O61—N6—O62 | 123.62 (15) |
| O1—C1—C6 | 122.88 (14) | O61—N6—C6 | 118.85 (14) |
| C2—C1—C6 | 111.17 (14) | O62—N6—C6 | 117.53 (14) |
| C3—C2—C1 | 124.06 (14) | C12—N11—C15 | 109.23 (16) |
| C3—C2—N2 | 115.19 (14) | C12—N11—H11 | 123.3 (13) |
| C1—C2—N2 | 120.72 (14) | C15—N11—H11 | 126.7 (13) |
| O22—N2—O21 | 121.74 (15) | N13—C12—N11 | 107.04 (16) |
| O22—N2—C2 | 120.29 (14) | N13—C12—C12A | 126.31 (18) |
| O21—N2—C2 | 117.97 (15) | N11—C12—C12A | 126.64 (18) |
| C2—C3—C4 | 119.73 (16) | C12—C12A—H12A | 112 (2) |
| C2—C3—H3 | 120.5 (11) | C12—C12A—H12B | 112.4 (16) |
| C4—C3—H3 | 119.7 (11) | H12A—C12A—H12B | 110 (2) |
| C3—C4—C5 | 121.00 (15) | C12—C12A—H12C | 111 (2) |
| C3—C4—N4 | 118.57 (15) | H12A—C12A—H12C | 104 (3) |
| C5—C4—N4 | 120.34 (15) | H12B—C12A—H12C | 107 (3) |
| O42—N4—O41 | 122.90 (16) | C12—N13—C14 | 110.12 (16) |
| O42—N4—C4 | 118.99 (15) | C12—N13—H13 | 125.4 (15) |
| O41—N4—C4 | 118.10 (15) | C14—N13—H13 | 124.5 (15) |
| C6—C5—C4 | 118.21 (15) | C15—C14—N13 | 106.55 (17) |
| C6—C5—H5 | 120.2 (12) | C15—C14—H14 | 132.4 (13) |
| C4—C5—H5 | 121.6 (12) | N13—C14—H14 | 121.0 (13) |
| C5—C6—C1 | 125.60 (15) | C14—C15—N11 | 107.06 (17) |
| C5—C6—N6 | 116.91 (14) | C14—C15—H15 | 132.4 (13) |
| C1—C6—N6 | 117.40 (14) | N11—C15—H15 | 120.5 (13) |
| O1—C1—C2—C3 | 179.72 (16) | C4—C5—C6—C1 | −0.5 (2) |
| C6—C1—C2—C3 | −4.2 (2) | C4—C5—C6—N6 | 175.84 (13) |
| O1—C1—C2—N2 | −2.4 (2) | O1—C1—C6—C5 | −179.73 (16) |
| C6—C1—C2—N2 | 173.62 (14) | C2—C1—C6—C5 | 4.1 (2) |
| C3—C2—N2—O22 | −163.80 (17) | O1—C1—C6—N6 | 3.9 (2) |
| C1—C2—N2—O22 | 18.2 (2) | C2—C1—C6—N6 | −172.26 (13) |
| C3—C2—N2—O21 | 16.4 (2) | C5—C6—N6—O61 | 129.43 (16) |
| C1—C2—N2—O21 | −161.61 (17) | C1—C6—N6—O61 | −53.90 (19) |
| C1—C2—C3—C4 | 0.9 (2) | C5—C6—N6—O62 | −51.0 (2) |
| N2—C2—C3—C4 | −177.07 (14) | C1—C6—N6—O62 | 125.64 (17) |
| C2—C3—C4—C5 | 3.3 (2) | C15—N11—C12—N13 | −0.36 (19) |
| C2—C3—C4—N4 | 179.90 (14) | C15—N11—C12—C12A | 178.83 (19) |
| C3—C4—N4—O42 | −6.2 (2) | N11—C12—N13—C14 | 0.53 (19) |
| C5—C4—N4—O42 | 170.49 (15) | C12A—C12—N13—C14 | −178.67 (18) |
| C3—C4—N4—O41 | 174.92 (16) | C12—N13—C14—C15 | −0.49 (19) |
| C5—C4—N4—O41 | −8.4 (2) | N13—C14—C15—N11 | 0.25 (19) |
| C3—C4—C5—C6 | −3.4 (2) | C12—N11—C15—C14 | 0.1 (2) |
| N4—C4—C5—C6 | −179.99 (15) |
Hydrogen-bond geometry (Å, °)
| D—H···A | D—H | H···A | D···A | D—H···A |
| C5—H5···O21i | 0.911 (19) | 2.478 (19) | 3.378 (2) | 169.4 (16) |
| N11—H11···O1 | 0.89 (2) | 1.95 (2) | 2.8357 (19) | 172.9 (19) |
| N13—H13···O1ii | 0.86 (2) | 2.09 (2) | 2.819 (2) | 143 (2) |
| N13—H13···O22ii | 0.86 (2) | 2.14 (2) | 2.782 (2) | 131.3 (19) |
Symmetry codes: (i) x, y, z−1; (ii) x, −y+3/2, z−1/2.
Footnotes
Supplementary data and figures for this paper are available from the IUCr electronic archives (Reference: DN2638).
References
- Altomare, A., Cascarano, G., Giacovazzo, C. & Guagliardi, A. (1993). J. Appl. Cryst. 26, 343–350.
- Du, M. & Zhao, X.-J. (2003). Acta Cryst. E59, o1898–o1900.
- MacDonald, J., Yigit, M. V. & Mychajlonka, K. (2005). Cryst. Growth Des. 5, 2248–2255.
- Nardelli, M., Pelizzi, G., Vitali, F., Bordi, F., Plazzi, P. V. & Vitali, T. (1987). Acta Cryst. C43, 507–514.
- Oxford Diffraction (2009). CrysAlis PRO Oxford Diffraction Ltd, Yarnton, Oxfordshire, England.
- Pi, M., Liu, X.-L., Xu, J.-J. & Jin, C.-M. (2009). Acta Cryst. E65, o2386. [DOI] [PMC free article] [PubMed]
- Sheldrick, G. M. (2008). Acta Cryst. A64, 112–122. [DOI] [PubMed]
- Siemens (1989). Stereochemical Workstation Operation Manual. Siemens Analytical X-ray Instruments Inc., Madison, Wisconsin, USA.
- Soriano-García, M., Schatz-Levine, M., Toscano, R. A. & Villena Iribe, R. (1990). Acta Cryst. C46, 1556–1558.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Crystal structure: contains datablocks I, global. DOI: 10.1107/S1600536810053390/dn2638sup1.cif
Structure factors: contains datablocks I. DOI: 10.1107/S1600536810053390/dn2638Isup2.hkl
Additional supplementary materials: crystallographic information; 3D view; checkCIF report